中国太极图理论的数学模型及应用

马如云(1964—)，男，甘肃天水人，教授，博士，博士研究生导师.主要研究方向为大范围分析和微分方程.E-mail:mary@nwnu.edu.cn

中国太极图理论的数学模型及应用

陈克恭,马如云

(西北师范大学，甘肃兰州730070)

摘要：本文对中国太极图建立了一个新的数学模型.模型兼容欧拉公式和毕达哥拉斯定理.它可以根据某属性的状态的平衡点和相对偏离量计算出相应的阳值和阴值，进而为相关实际决策提供可靠的理论依据.

关键词：太极图；数学模型；相对偏离量；阳阴值；欧拉公式；毕达哥拉斯定理

收稿日期：2015-09-10;修改稿收到日期:2015-09-14

基金项目:国家自然科学基金资助项目(11361054)

作者简介：陈克恭(1961—)，男，甘肃兰州人，研究员，硕士，博士研究生导师,西北师范大学党委书记.主要研究方向为自然地理学.E-mail:chenkg@nwnu.edu.cn

中图分类号：O 112文献标志码：A

Mathematical model on Chinese Yin-and-Yang

double-fish diagram and its application

CHEN Ke-gong,MA Ru-yun

(Northwest Normal University,Lanzhou 730070,Gansu,China)

Abstract:In this paper,we establish a mathematical model for chinese Yin-and-Yang double-fish diagram.This model is compatible with the well-known Euler formula and Pythagorean theorem.It can be used to determine the Yin value and Yang value with respect to equilibrium point and of the relative deviation,so that it can provide reliable theoretical foundation for making a strategic decision.

Key words:Yin-and-Yang double-fish diagram;mathematical model;relative deviation;Euler formula;Pythagorean theorem

0引言

普通高等教育“十五”国家级规划教材《中医基础理论》中关于阴阳的定义是：“阴阳，是中国古代哲学的一对范畴，是对自然界相互关联的某些事物或现象对立双方属性的概括”.当前很多研究者认为：似乎什么都是阴阳，阴阳又什么都不是.阴阳玄虚莫测、难以捉摸却施之有效.王正山[4]从阴阳的本义出发，区分了“抽象阴阳”与“具体阴阳”.其中，“抽象阴阳”是抽象意义上的阴阳，所指无定在，比较模糊笼统；“具体阴阳”是具体属性上的阴阳，所指明确，可以测量，具有确定性和可判定性.笔者赞同文[4]的观点和作法.

传统的阴阳学说长于定性，而短于定量，缺乏严格性和精确性，这是阴阳学说与时俱进的一大障碍.鉴于此，不少学者尝试从数学的角度来研究阴阳学说.其中比较有影响的成果有：赵喜新[1]由自然界的阴阳转化现象出发，提出了阴阳消长平衡转化的正弦函数式.翟忠信[2]提出了一个动态数学模型，该模型将阴阳定义为一个二维的空间，二维空间中的每个点都是机体的一个阴阳态，再引入一个时间轴，通过对这一模型的稳定性分析，解释了由机体阴阳状态的交化所产生的多种病理现象.吴昌国[3]引用数学的复数概念，为阴阳理论的多种应用形式确立表达式，从复数的虚实相关性对应地探讨阴阳之间的特殊关系形式.王正山在其博士学位论文[4]中阐明阴阳是一种二元关系，并讨论了中医阴阳虚实的含义及度量方法.但该文关于阴阳此消彼长的数量关系没有深入探讨.李金林[5]提出了阴阳相关性的泛系模型，赵致镛[6]等建立了阴阳之间的微积分公式和阴阳定量与药物定量之间的数学表达式，秦建增[7]等采用二进制数字语言对阴阳理论进行了数字编码，完成了对中医学阴阳理论的数字模型的构建.

本文拟通过引进单纯属性层面的概念，在适当的假设下，对太极阴阳图建立一个新的数学模型.该模型可以根据某属性状态的相对偏离量计算出相应的阳值和阴值，进而为阴阳理论的实际决策提供可靠的理论依据.我们的模型将很好地兼容欧拉公式和毕达哥拉斯定理.

单纯属性层面的定义：研究阴阳属性时的工作层面，在其上仅有同一个属性上的两种相反的状态的演化被考察，而其它任何属性及其演化均被忽略.

本文后面总假设

H1.在单纯属性层面E上，有一个属性P下的两种相反的状态，该属性可以通过一维数值定量刻画.

H2.该属性上的两种相反的状态，相互依存，此消彼长，并且它们可以围绕一个常态(平衡点)波动或演化.

例1考察一个患者的体温情况，单纯属性层面即为“体温层面”，其上属性为体温属性，体温属性有高温和低温两种相反的状态.体温属性可以通过温度计定量刻画.温度高低两种状态可以在正常体温值周围上下波动.

1单纯属性层面上属性的度量

假设H1,H2成立.

设T为属性P的常态(平衡点)，(T-a,T+b)为属性P的正常值范围.

设T+c为属性P在某状态A下的取值，则状态A的绝对偏移量为

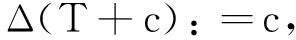
其中c∈(-a,b).定义状态A的相对偏移量为

则δ∈[-1,1].相对偏移量是比值，故没有量纲.

注1:本文提出的相对偏移量，不同于[4]中给出的三种相对偏移量.它更有利于处理正负向振幅不相等的非对称振荡属性波形的阴阳问题.

注2:本文假设中的平衡点一般通过积分法求曲边梯形的面积对底边的平均来获得.例如，设某正常人的体温随时间的变化曲线函数为f(t),t∈[0,T]，则平衡点(平均体温)应为

为求相对偏差量而先求绝对偏差量时，若数据振荡幅度较大，则应通过积分法求曲边梯形的面积对底边的平均来获得“平均意义下”绝对偏差量，而不应只利用观测数据的最大数值来获得绝对偏差量.

2太极图定量模型

建立直角坐标系.以坐标原点为中心1为半径作圆，以纵轴表示状态的相对偏移量.设状态的相对偏移量为δ，坐标(0,δ)在纵轴上的点记作N，过N作水平线交圆周于B,B′两点.过原点O作∠AOB的平分线OC(图1).

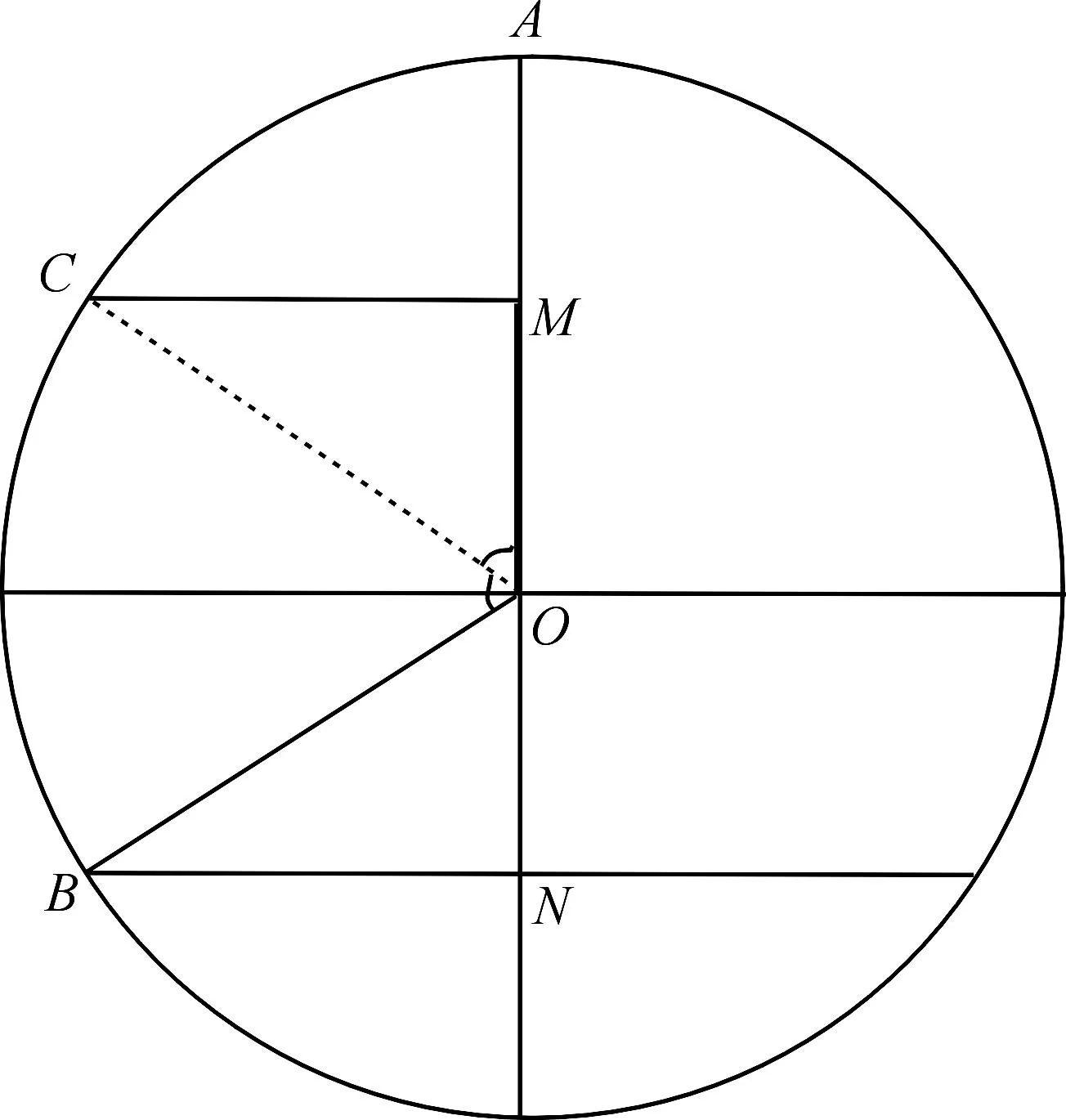
图1　B点的阳值为线段

定义状态的相对偏移量的坐标为(0,δ)时的阳值和阴值分别为

由于

又cos∠AOB=δ，故我们有如下结果

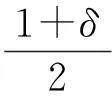
相对偏移量为δ时的阴阳赋值亦称为单位圆上B点或B′点的阴阳赋值.注意：阳赋值为角∠AOB的平分线与圆周的交点C在纵轴上的投影M所对应的相对偏移量的平方.

注3阴阳值依赖于正常值范围(-a,b)的大小.显然相对阴阳值只能是指给定范围前提下的阴阳值.在绝对偏差量不变的前提下，正常值范围变大，相对偏差量会变小，进而相应的阳值变小、阴值变大.反之亦然(图2-3).

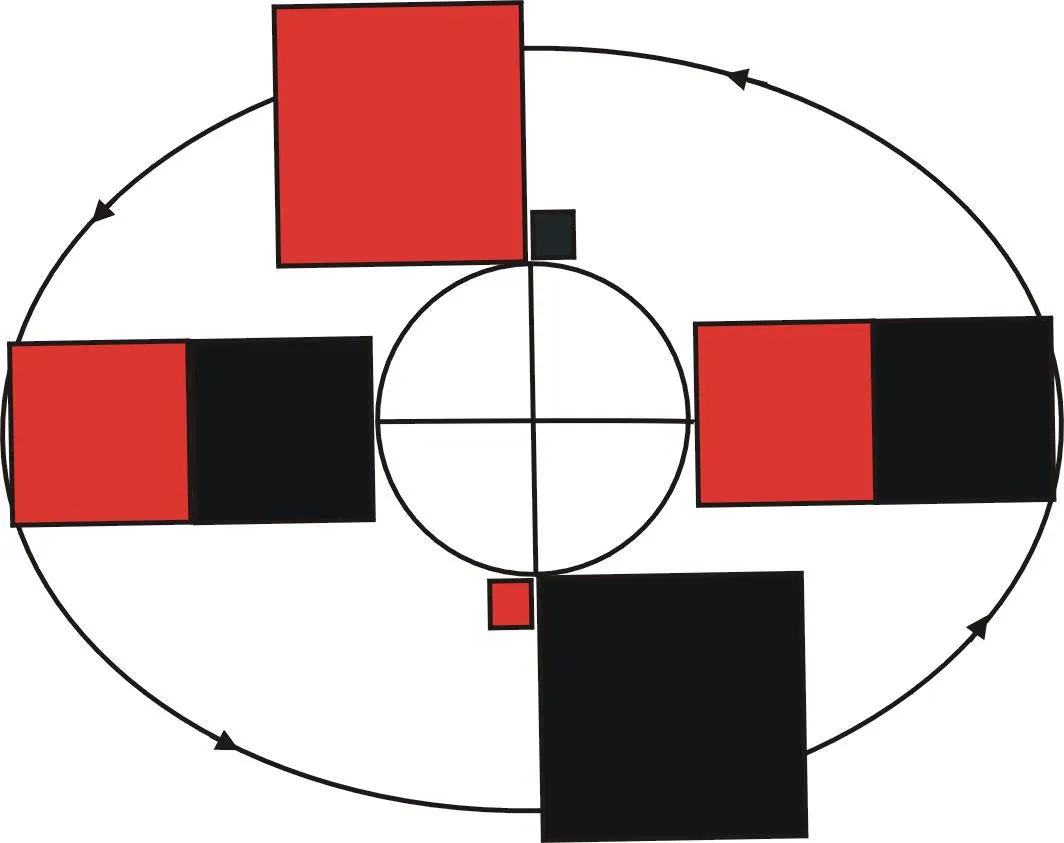
图2　新数学模型下太极图模型示意

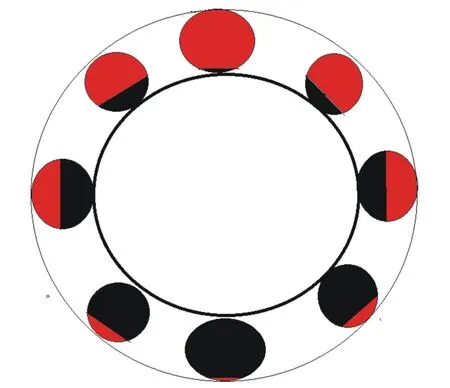
图3　 新数学模型下太极图模型示意图

记阳函数和阴函数分别为

其中x=∠AOB.显然，P(x)和N(x)均为以2π为周期的周期函数(图4).

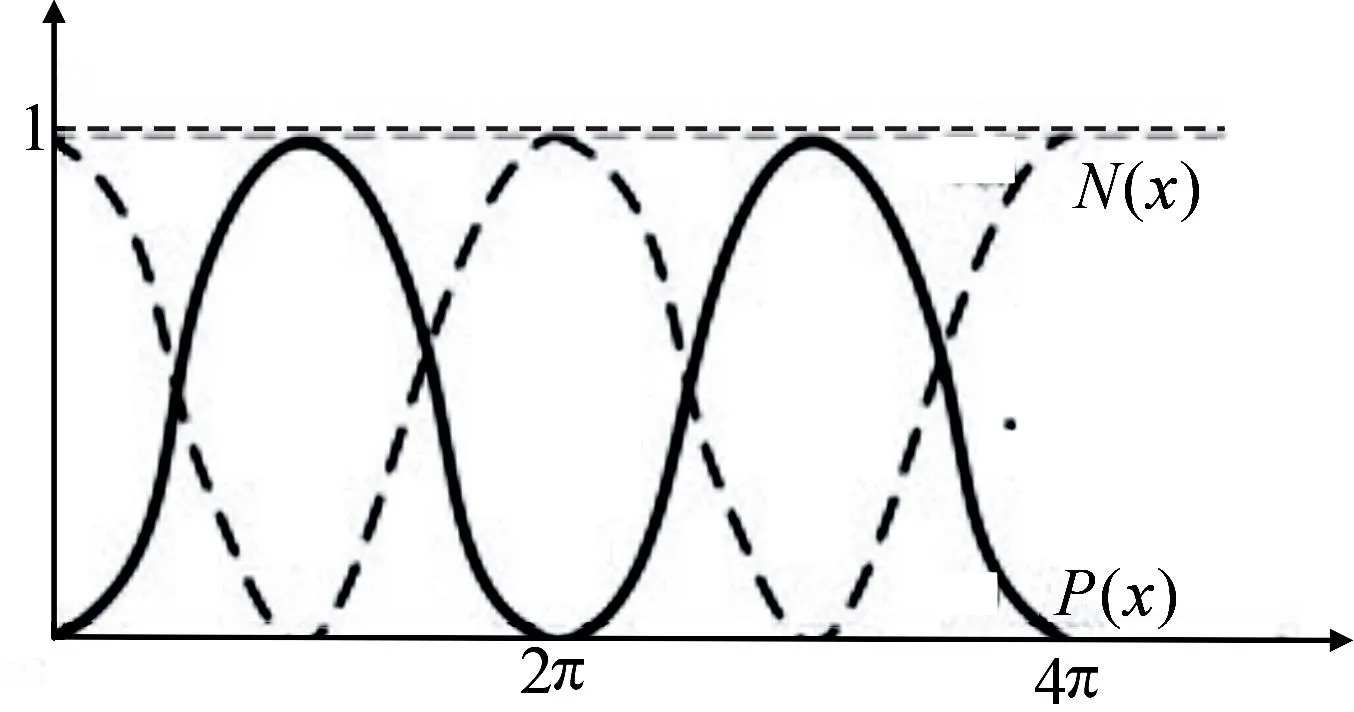
图4　阳函数与阴函数曲线

注4:阴阳值依赖于平衡点在正常值范围(T-a,T+b)的位置.新常态下状态的阴阳值均会发生改变.比如：经济增速从7.7%(原常态)降至新常态的增速7.0%.对于7.2%的实际速度而言，在原常态下，阴值>阳值；而在新常态下，阳值>阴值.

3太极图定量模型的应用

3.1与原太极阴阳图意义匹配

本文以M所对应的相对偏移量的平方计算阳赋值，符合太极图所体现的“阴阳总和不变的思想”.但太极阴阳图只是一个意向图，显示不出太极的具体数量关系.

图5　太极阴阳图(阴阳面积之和为1)

3.2对Euler公式的解释

“至阳1”旋转π=180°得到“至阴 -1”

3.3对毕达哥拉斯定理的解释

这与阴阳理论完全一致.毕达哥拉斯定理又名勾股定理，它是代数与几何的完美结合.

图6　勾股定理示意图

3.4药物定量

可以根据患者某些重要属性的阴阳值，合理施药，达到阴阳均衡的目的.有效防止用药过量或用药不足的现象发生.

3.5张掖沙水系统分析

张掖沙水系统上的单纯属性层面为理想化的纯沙水系统,其上属性为沙漠面积(或不可灌溉面积),取水沙现象常态的面积值为平衡点.沙漠面积大小两种状态可以在围绕平衡点上下波动.可以依据实际测量数据和本文的数学模型，给出张掖沙水系统的阴阳数值，进而为决策提供参考.

太极图的定量模型，对于我国阴阳学说在世界范围的推广具有重要意义.特别地，在特定的属性P下，太极图的定量模型有特定的实际意义.

参考文献:

[1]赵喜新．中医阴阳学说的数学模型[J].河南中医，1997，17(5)：264.

[2]翟忠信．中医阴阳学说的一个数学模型[J].数理医药学杂志，1999，12(4)：302．

[3]吴昌国．复数在中医阴阳理论中的应用研究[J].中国中医基础医学杂志，2002，8(4)：65.

[4]王正山.中医阴阳的本质及相关问题研究[D].北京：北京中医药大学，2014.

[5]李金林.阴阳相关性的泛系模型[J].西北民族学院学报(自然科学版)，2002，23(1)．

[6]赵致镛，赵威.中医阴阳理论的数学模型之建立及其徼积分定量的研究[J].四川中医，2005，23(11):8.

[7]秦建增，陈宝田.中医阴阳数字模型[J].第一军医大学学报，2004，24(8)：933.

(责任编辑俞诗源)