2016年高考数学模拟金卷（二）

赵银仓

一、选择题：本大题共8小题，每小题5分，共40分.

1. （理）已知全集U=R，S={xx=2t}，T={xln（x-1）<0，则S∩T等于（ ）

A. ■ B. {x0

C. {x0

（文）定义A-B={xx∈A，且x？埸B}. 若M={1，2，3，4， 5}，N={2，3，6}，则M-N等于（ ）

A. M B. N C. {6} D. {1，4，5}

2. （理）设复数e■=cosθ+isinθ，则复数e■的虚部为（ ）

A. ■ B. ■ C. ■i？摇 D. ■i

（文）已知■=1-ni，其中m，n是实数，i是虚数单位，则m+n？摇等于（ ）

A. 3 B. 2 C. 1 D. -1

3. 若a=■，sinα，b=cosα，■，且a∥b，则锐角α等于（ ）

A. 15° B. 30° C. 45° D. 60°

4. 下列命题中，其中假命题是（ ）

A. 对分类变量X与Y的随机变量K2的观测值k来说，k越小，“X与Y有关系”可信程度越大

B. 用相关指数R2来刻画回归的效果时，R2的值越大，说明模型拟合的效果越好

C. 两个随机变量相关性越强，则相关系数的绝对值越接近1

D. 三维柱形图中柱的高度表示的是各分类变量的频数

5. 若Sn是等差数列{an}的前n项和，且S8-S3=10，则S11的值为（ ）

A. 12 B. 18 C. 22 D. 44

6. （理）设x，y满足约束条件3x-y-6≤0，x-y+2≥0，x≥0，y≥0，若目标函数z=ax+by（a>0，b>0）的最大值为12，则■+■的最小值为（ ）

A. ■ B. ■ C. ■ D. 25

（文）已知椭圆C：■+■=1（a>b>0）的离心率为■. 双曲线x2-y2=1的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为（ ）

A. ■+■=1 B. ■+■=1

C. ■+■=1 D. ■+■=1

7. （理）设集合S={A0，A1，A2}，在S上定义运算⊕：Ai⊕Aj=Ak，其中k为i+j被3除的余数，则使关系式（Ai⊕Aj）⊕Ai=A0成立的有序数对（i，j）总共有（ ）

A. 1对 B. 2对 C. 3对 D. 4对

（文）同理科第6题.

8. （理）如图1，F1，F2分别是双曲线C：■-■=1（a>0，b>0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M. 若MF2=F1F2，则C的离心率是（ ）

A. ■ B. ■ C. ■ D. ■

（文）已知y=f（x）是二次函数，若x=1是函数y=f（x）ex的一个极值点，则下列函数图象不可能为y=f（x）的图象的是（ ）

■

A B C D

二、填空题：本大题共8小题，考生作答7小题，每小题5分，共35分.

（一）选做题（请理科考生在9、10、11三题中任选两题作答，如果全做，则按前两题记分；请文科考生在9、10两题中任选一题作答，如果全做，则按第9题记分）

9. （理）（坐标系与参数方程选讲）在平面直角坐标系xOy中，曲线C1和C2的参数方程分别为x=t，y=■（t为参数）和x=■cosθ，y=■sinθ（θ为参数），则曲线C1与C2的交点坐标为________.

（文）（坐标系与参数方程选讲）直线2ρcosθ=1与圆ρ=2cosθ相交的弦长为___________.

10. （几何证明选讲）如图2，点D在圆O的弦AB上移动， AB=4，连结OD，过点D作OD的垂线交圆O于点C，则CD的最大值为__________.？摇

11. （理）（不等式选讲）若存在实数x使x-a+x-1≤3成立，则实数a的取值范围是___________.

（二）必做题（理科12～16题；文科11～16题）

11. （文）学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n的样本，其频率分布直方图如图3所示，若已知其中支出在[40，50）元的同学有39人，则n的值为_________.

12. 执行如图4所示的程序框图，则输出的S的值为_________.

13. 有下列四个命题：

①？埚x0∈R，e■≤0；

②？坌x∈R，2x>x2；？摇

③a+b=0的充要条件是■=-1；

④a>1，b>1是ab>1的充分条件.

其中真命题是________.

14. 已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为____________.

15. （理）设点P在曲线y=■ex上，点Q在曲线y=ln（2x）上，则PQ的最小值为_________.

（文）定义在R上的函数f（x）满足f（x+6）=f（x）. 当-3≤x<-1时，f（x）=-（x+2）2；当-1≤x<3时，f（x）=x. 则f（1）+f（2）+f（3）+…+f（2013）=_________.

16. （理）C为线段AB上的中点，P为直线AB外一点，满足■=■=3，■-■=4，■=λ■，■=■+m■+■，m>0，则λ=_________.

（文）如图5，命题：点A1，A2是线段AB的三等分点，则有■+■=■+■. 现把此命题推广：设点A1，A2，A3，…，An-1是AB的n等分点（n≥3），则有■+■+…+■=_______（■+■）.

三、解答题：本大题共6小题，共75分.

17. （本小题满分12分）已知向量m=（■sin2x+2，cosx），n=（1，2cosx），设函数f（x）=m·n.

（1）求f（x）的最小正周期与单调递增区间；

（2）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=4，b=1，△ABC的面积为■，求a的值.

18. （本小题满分12分）（理）为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中微量元素x，y的含量（单位：毫克）. 下表是乙厂的5件产品的测量数据：

■

（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；

（2）当产品中的微量元素x，y满足x≥175且y≥75时，该产品为优等品. 用上述样本数据估计乙厂生产的优等品的数量；

（3）从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数ξ的分布列及其均值（即数学期望）.

（文）在某次测验中，有6位同学的平均成绩为75分. 用xn表示编号为n（n=1，2，…，6）的同学所得成绩，且前5位同学的成绩如下：

■

（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s；

（2）从前5位同学中，随机地选取2位同学，求恰有1位同学成绩在区间（68，75）中的概率.

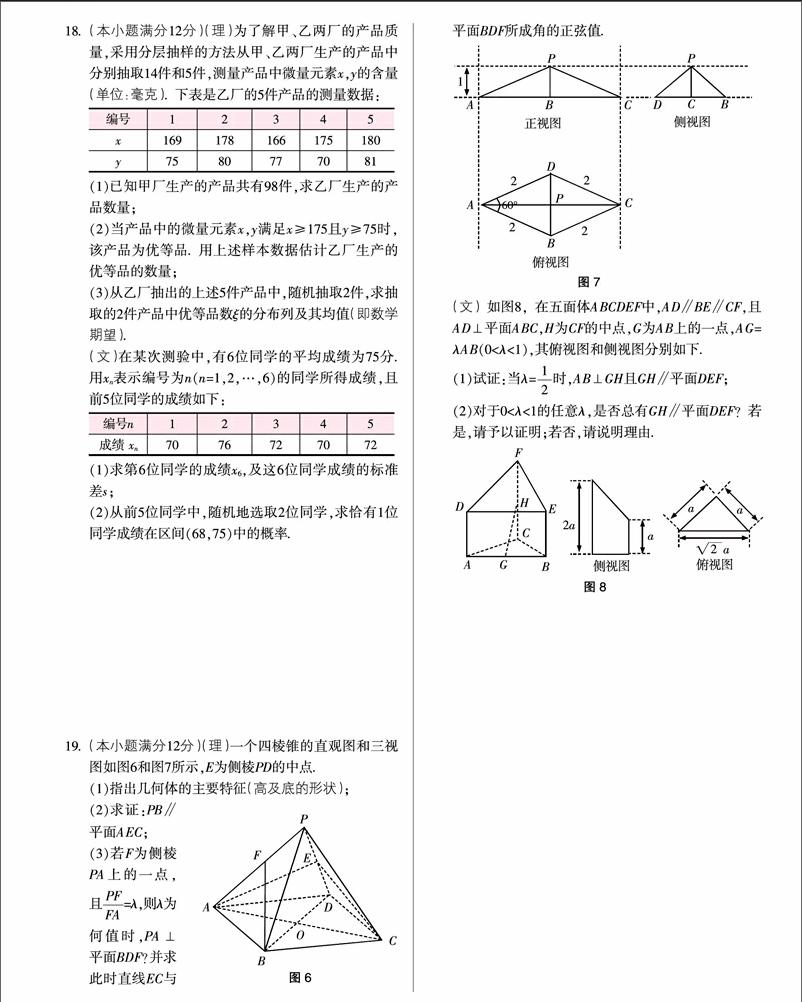
19. （本小题满分12分）（理）一个四棱锥的直观图和三视图如图6和图7所示，E为侧棱PD的中点.

（1）指出几何体的主要特征（高及底的形状）；

（2）求证：PB∥平面AEC；

（3）若F为侧棱PA上的一点，且■=λ，则λ为何值时，PA⊥平面BDF？并求此时直线EC与平面BDF所成角的正弦值.

（文）如图8，在五面体ABCDEF中，AD∥BE∥CF，且AD⊥平面ABC，H为CF的中点，G为AB上的一点，AG=λAB（0<λ<1），其俯视图和侧视图分别如下.？摇

（1）试证：当λ=■时，AB⊥GH且GH∥平面DEF；

（2）对于0<λ<1的任意λ，是否总有GH∥平面DEF？若是，请予以证明；若否，请说明理由.

■

图8

20. （本小题满分13分）（理）设抛物线C：x2=2py（p>0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点.

（1）若∠BFD=90°，△ABD的面积为4■，求p的值及圆F的方程；

（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值.

（文）某工厂生产一种仪器的元件，由于受生产能力和技术水平等因素的限制，会产生一些次品，根据经验知道，次品数P（万件）与日产量x（万件）之间满足关系：P=■x2，1≤x<4，x+■-■，x≥4.已知每生产1万件合格的元件可以赢利2万元，但每生产1万件次品将亏损1万元. （利润=赢利-亏损）

（1）试将该工厂每天生产这种元件的利润T（万元）表示为日产量x（万件）的函数；

（2）当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大，最大利润为多少？

21. （本小题满分13分）（理）已知函数f（x）=2a2lnx-x2（常数a>0）.

（1）当a=1时，求曲线y=f（x）在x=1处的切线方程；

（2）讨论函数f（x）在区间（1，e2）上零点的个数（e为自然对数的底数）.

（文）同理科第20题.

22. （本小题满分13分）（理）已知等比数列{an}的首项为a1=2，公比为q（q为正整数），且满足3a3是8a1与a5的等差中项；数列{bn}满足2n2-（t+bn）n+■bn=0（t∈R，n∈N*）.

（1）求数列{an}的通项公式；

（2）试确定t的值，使得数列{bn}为等差数列；

（3）当{bn}为等差数列时，对任意正整数k，在ak与ak+1之间插入b■k个2，得到一个新数列{cn}. 设T■n是数列{cn}的前n项和，试求满足Tm=2cm+1的所有正整数m的值.

（文）形如a bc d的式子叫做二行二列矩阵，定义矩阵的一种运算a bc d·xy=ax+bycx+dy. 该运算的几何意义为平面上的点（x，y）在矩阵a bc d的作用下变换成点（ax+by，cx+dy）.

（1）设点M（-2，1）在0 11 0的作用下变换成点M′，求点M′的坐标；

（2）设数列{an}的前n项和为Sn，且对任意正整数n，点A（Sn，n）在0 11 0的作用下变换成的点A′在函数f（x）=x2+x的图象上，求an的表达式；

（3）在（2）的条件下，设bn为数列1-■的前n项的积，是否存在实数a使得不等式？摇bn■