忆阻蔡氏对偶混沌电路分析

陆安山，陆益民

(1.广西大学 电气工程学院，广西 南宁 530004;2.钦州学院 物理与电子工程学院，广西 钦州 535000)

忆阻蔡氏对偶混沌电路分析

陆安山1,2，陆益民1

(1.广西大学 电气工程学院，广西 南宁 530004;2.钦州学院 物理与电子工程学院，广西 钦州 535000)

摘要：提出了用分段单调荷控忆阻器代替对偶蔡氏混沌电路中的非线性电阻，构造出基于忆阻器的对偶蔡氏混沌电路。对该忆阻蔡氏对偶混沌电路的理论推导、稳定性、Lyapunov指数和数值仿真等动力学特性进行了分析。研究结果表明：该系统为双涡卷混沌吸引子，该忆阻蔡氏对偶混沌电路的动力学特征对初值敏感异于普通混沌电路。

关键词：忆阻器；对偶混沌电路；数值分析

基金项目：国家自然科学基金项目(51167002);广西高校科学技术研究项目(2013YB256)

作者简介：陆安山(1970-),男,广西钦州人,副教授,主要从事电子技术、混沌同步与控制方面的研究.

收稿日期：2014-09-03

文章编号：1672-6871(2015)02-0092-04

中图分类号：O415.5

文献标志码：志码：A

0引言

1971年，华裔科学家Chua L.O发表了名为《Memristor-the Missing Circuit Element》[1]的论文，第1次提出记忆电阻器(忆阻器)的概念，并对忆阻器的性能与应用进一步阐述[2]。2008年，惠普公司的Dmitri B.Strukov等人在实验室中成功研制出第1个忆阻器元件，并在《Nature》发表论文《The Missing Memristor Found》[3]。由于忆阻器构造的电路具有无源准则、自由度准则和闭合准则[4]以及线性时变和线性时不变特性等特点，并在人工智能、模拟电路、存储器等方面具有广泛应用价值，因而受到广泛关注[5-7]。

忆阻器是一个无源非线性器件，引入电路中易产生混沌振荡信号。因此，利用忆阻器件构造基于忆阻混沌电路是目前构造混沌电路的一个研究方向。近年来，文献[4]用忆阻器替换蔡氏电路中的蔡氏负阻，导出了基于忆阻器的混沌振荡电路。文献[8]用一个有源磁控忆阻器替换蔡氏振荡器中的蔡氏二极管，实现了一个五阶混沌电路。文献[9]用含磁控和荷控两种忆阻器设计出混沌电路，这些混沌电路的拓扑结构都较复杂，电路实现难度大。本文提出以忆阻器替换蔡氏对偶混沌电路[10]中的非线性电阻元件，构造一个四阶混沌电路，利用混沌动力学理论对其稳定性、Lyapunov指数、耗散性和吸引子存在性、初值敏感性进行了分析，并用数值仿真进行了验证。

1忆阻蔡氏对偶混沌电路

记忆电阻器是一个基本的无源二端器件，其磁通φ与电荷q之间的关系可用φ-q或q-φ表示，可分为荷控忆阻器和磁控忆阻器两种[1-3]，如图1所示。图1a的荷控忆阻器可用q-φ平面上通过原点的曲线φ=φ(q)来表示，其斜率M(q)称为忆阻，M(q)=dφ(q)/dq；图1b的磁控忆阻器可用φ-q平面上通过原点的曲线q=φ(q)来表示，其斜率W(φ)称为忆导，W(φ)=dq(φ)/dφ。

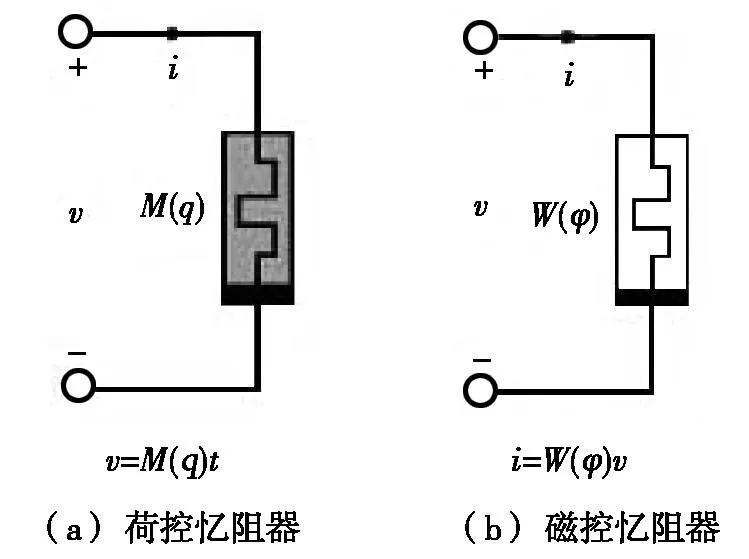
图1　忆阻器

本文在蔡氏对偶混沌电路[10]基础上，用一个荷控忆阻器替代蔡氏对偶混沌电路非线性元件，提出一个基于忆阻蔡氏对偶混沌电路，如图2所示。其中，忆阻器满足单调递增和分段线性的特点，关系式如下：

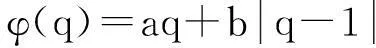
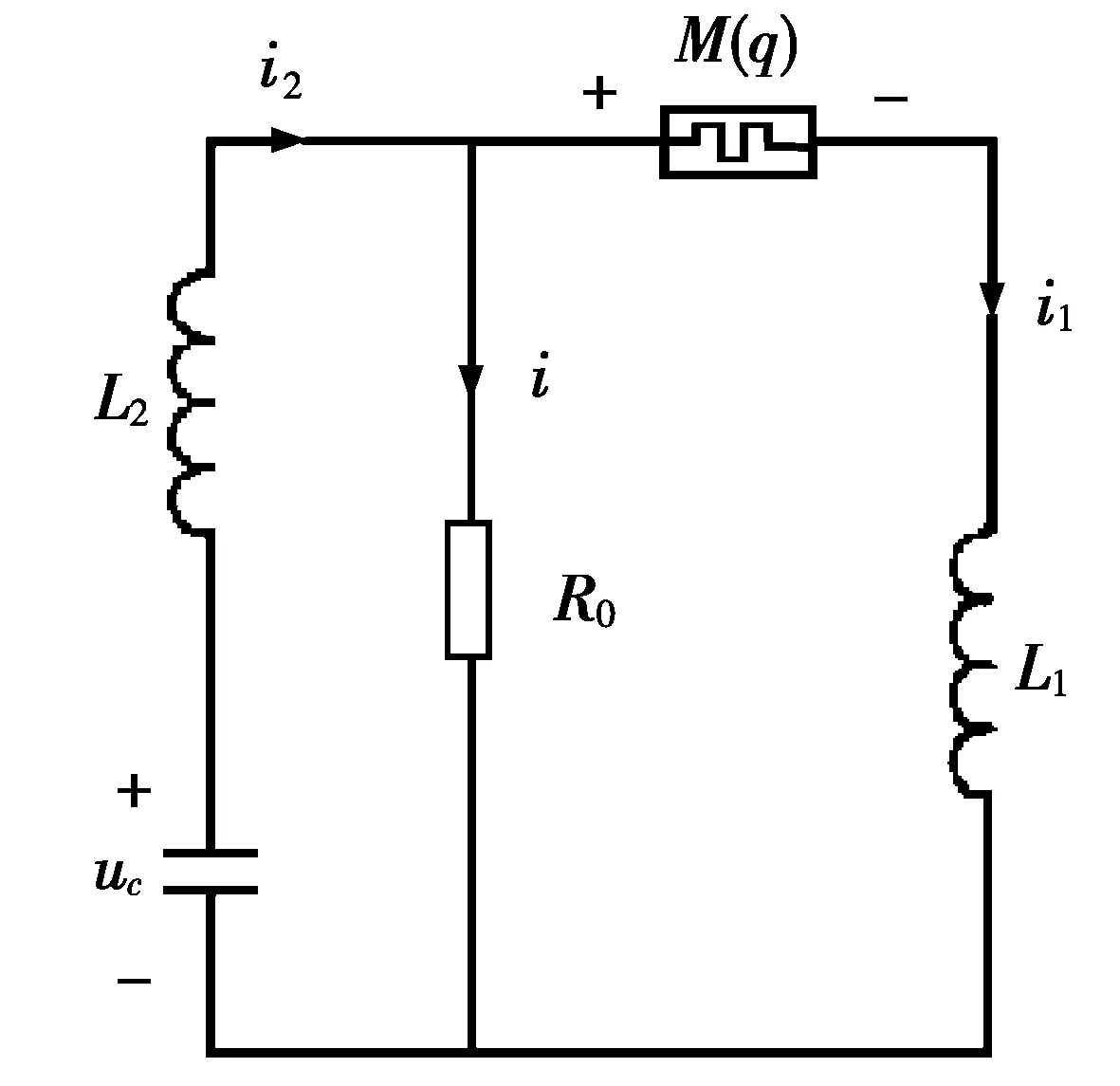
图2　忆阻蔡氏对偶混沌电路

根据电路原理，图2的电路方程如下：

(1)

(2)

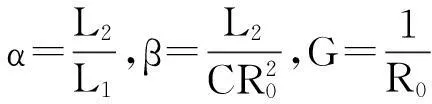
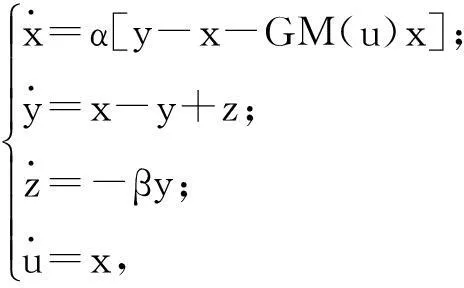
(3)

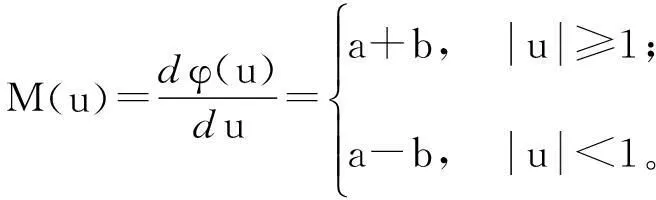
2动力学分析

2.1　稳定性分析

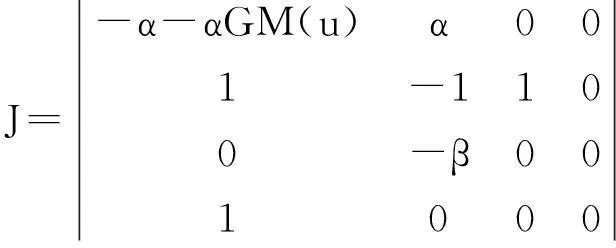
取L1=0.001，L2=0.008，C=6.4×10-4，R0=1，a=-0.8，b=0.3；则α=8，β=12.5，G=1时，

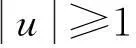
则由线性稳定性定理可知，该系统在平衡点A处不稳定，该平衡点为不稳定鞍焦点。

2.2　Lyapunov指数

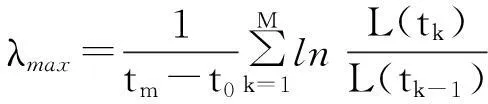
用Jacobian方法求得该系统的Lyapunov指数分别为：LE1=0.039 5,LE2=0.016 2，LE3=-0.229 8，LE4=-2.622 0；Lyapunov指数维数dL=2.933 6，为分数，表明该系统为Lyapunov意义下的混沌系统。

2.3　系统的耗散性和吸引子存在性分析

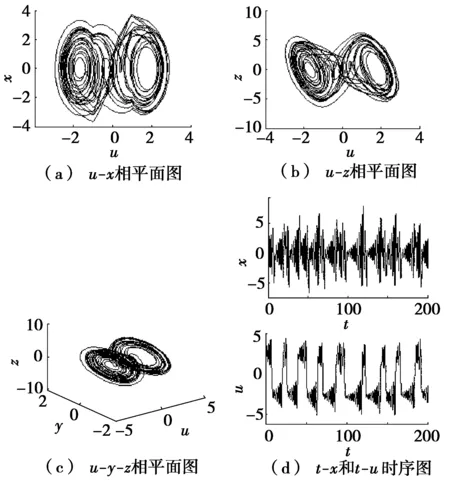
图3　相轨迹及时序图

3仿真分析

3.1　相轨迹及时序图绘制

式(3)参数取L1=0.001，L2=0.008，C=6.4×10-4，R0=1，a=-0.8，b=0.3；则α=8，β=12.5，G=1；在初始条件为(0,0.3,0,0)时，用Matlab仿真绘制系统的相轨迹及时序图，如图3所示。图3a和图3b分别给出了混沌吸引子在u-x、u-z平面上的投影，为双涡卷混沌吸引子；图3c是混沌吸引子三维空间上的投影，图3d是变量x和u的时域波形图，它们是非周期的，貌似随机的。所以，从该系统的稳定性、时域波形、相轨迹以及Lyapunov指数和维数可知：该系统是混沌振荡的。

3.2　相轨迹分析

对系统(3)固定参数α=8、β=12.5、G=1，u取不同的初值，其相轨迹如图4所示。图4a和图4b表明：u(0)取两个绝对值相同的数值时，该系统混沌吸引子，它们的拓扑结构具有复合结构并关于坐标原点形成中心对称。图4c和图4d是周期极限环；图4e和图4f是混沌系统突变的两相轨迹图。由图4可看出：该忆阻混沌系统在不同初值时存在与普通混沌系统完全不一样的运动轨迹，轨迹可能会在混沌、周期或稳定之间发生状态转移。

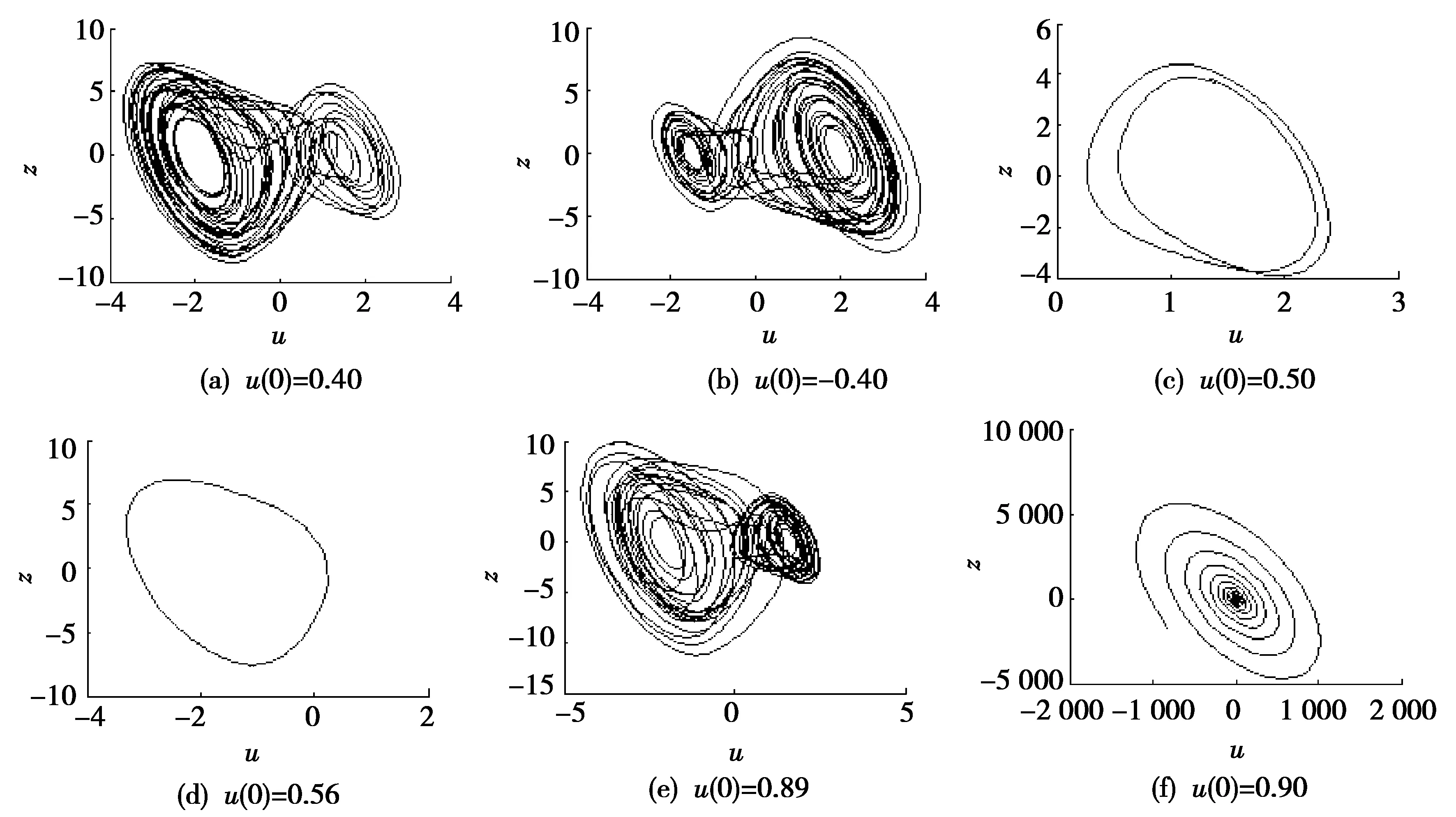
图4　u取不同初值时u-z平面相轨迹

4结束语

本文提出利用一个分段非线性磁控忆阻器替代对偶蔡氏混沌电路中的非线性电阻，得到一个新的基于忆阻器的混沌系统。该系统的动力学分析、数值仿真结果表明：系统能产生双涡卷混沌吸引子，该吸引子轨线在吸引域内具有遍历性和混合性，具有分数维，有别于普通混沌系统的初值敏感性。改变初值可以实现其从周期向混沌、稳定状态的过渡，与忆阻器内部状态有密切关联。系统的混沌行为更为复杂，对信号隐匿与包含的调解更有利，对非预知的解调更难，对保密通讯等方面的应用有一定的价值，可为基于忆阻器混沌电路的构造提供一种思路。

参考文献：

[1]Chua L O.Memristor-the Missing Circuit Element[J].IEEE Transactions on Circuit Theory,1971,18(5):507-519.

[2]Chua L O,Kang S M.Memrisive Devices and Systems[J].Proceedings of the IEEE,1976,64(2):209-223.

[3]Strukov D B,Snider G S,Stewart D R,et al.The Missing Memristor Found[J].Nature,2008,453(1):80-83.

[4]Itoh M,Chua L O.Memristor Oscillators[J].International Journal of Bifurcation and Chaos,2008,18(11):3183-3206.

[5]Ebong I E，Mazumder P.CMOS and Memristor-based Neural Networkdesign for Position Detection[J].Proceedings of the IEEE,2012,100(6):2050-2060.

[6]Hyongsuk K，Sah M P，Yang C J，et al.Neural Synaptic Weightingwith a Pulse-based Memristor Circuit[J].IEEE Trans Circuits Syst,2012,59(1):148-158.

[7]杨芳艳.基于Chua电路的四维超混沌忆阻电路[J].物理学报,2014,63(8):080502-1-8.

[8]包伯成,王其红,许建平.基于忆阻元件的五阶混沌电路研究[J].电路与系统学报,2011,16(2):66-70.

[9]洪庆辉,曾以成,李志军.含磁控和荷控两种忆阻器的混沌电路设计与仿真[J].物理学报,2013,23:49-55.

[10]刘崇新.蔡氏对偶混沌电路分析[J].物理学报,2002,51(6):1198-1202.