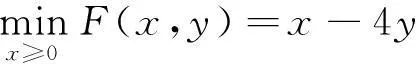求二层线性规划最优解的极点方法

求二层线性规划最优解的极点方法*

赵礼阳1， 霍永亮2

(1.重庆师范大学 数学学院,重庆 401331;2.重庆文理学院 数学与财经学院,重庆 402160)

摘要：根据二层线性规划的最优解一定可以在约束集的极点找到这一理论，给出了求解二层线性规划的极点方法，通过上层目标函数值的排序，避免了盲目验证极点这一缺陷，最后通过算例描述了算法求解过程，并验证了算法的有效性.

关键词：二层线性规划；约束条件；全局最优解；极点

doi:10.16055/j.issn.1672-058X.2015.0011.021

收稿日期：2015-04-14；修回日期：2015-05-20.

基金项目：*重庆高校创新团队建设计划项目(KJ301321).

作者简介：赵礼阳(1990-)，男，重庆大足人，硕士研究生，从事最优化理论研究.

中图分类号：O221.5文献标志码：A

0引言

考虑如下二层线性规划问题(LBP)：

s.t.Ax+Bx≤b

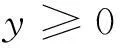
(1)

二层线性规划问题是二层规划问题中最简单的一种类型，在二层线性规划问题中，其目标函数和约束条件都是线性存在的[1,2].对于二层规划，由于下层目标函数要以上层决策变量作为参数，上层又要以下层最优解反馈作为条件达到上层的最优，使得二层规划比一般的数学规划为更为复杂[3].

Candler[4]和Townsley[5]在研究上层为无约束，且下层有唯一解的二层线性规划时得到一个有趣的性质：假设二层线性规划的最优解个数为有限个，那么在约束集的极点(顶点)处，至少存在一个极点是该问题的最优解.之后，Bard在约束集有界的前提下，证明了这是二层线性规划的一个共性[6].

此处根据二层线性规划的全局最优解一定可以在约束域极点找到的理论，首先求出约束域的所有极点，根据极点处上层目标函数的值由小到大进行极点排序，然后按照这个顺序进行最优解检验，最终确定问题的全局最优，此处最后通过算例验证了算法的有效性.

1基本理论

定义1IR={(x,y):(x,y)∈S,y∈P(x)}为式(1)的可归纳域(可行集).

为了保证式(1)有解，假设S为非空有界闭集；并且对于任意给定的上层决策变量，下层都只有唯一最优解反馈给上层.

定义2称(x*,y*)为问题(LBP)的全局最优解，简称最优解.如果存在(x*,y*)∈IR，使得对任意的(x,y)∈IR，都有F(x*,y*)≤F(x,y)成立[7].

定义3如果(x0,y0)是S的任意一个极点(顶点)，则对于S中相异于(x0,y0)的任意两点(x1,y1),(x2,y2)∈S，以及任意的实数λ>0，λ∈(0,1)，下面等式(2)不成立.

(2)

定理1如果(x0,y0)是式(1)的唯一最优解，则(x0,y0)必是式(1)约束集的极点.

证明反证法.假设(x0,y0)是式(1)的唯一最优解，但(x0,y0)不是式(1)约束集的顶点，则由定义3可得，存在(x1,y1),(x2,y2)∈S，且(x1,y1)≠(x0,y0)，(x2,y2)≠(x0,y0)，存在一正数λ∈(0,1)，等式(3)成立：

(3)

于是有λx1+(1-λ)x2=x0，λy1+(1-λ)y2=y0，那么(λx1+(1-λ)x2,λy1+(1-λ)y2)也是式(1)的最优解，显然成立等式(4)：

(4)

又因为(x0,y0)是式(1)的唯一最优解，则

(5)

(6)

λ与(1-λ)分别乘入式(5)(6)，相加得

这就与F(x0,y0)=F(λx1+(1-λ)x2,λy1+(1-λ)y2)矛盾，故定理得证.

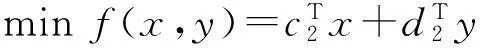
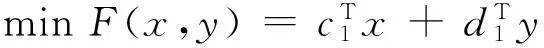
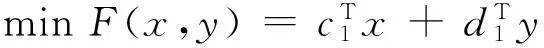
于是成立等式：

(7)

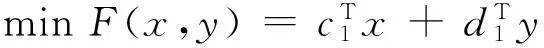
2算法描述

因为线性二层规划的全局最优解一定出现在该问题约束集的极点处，因此在约束集空间的极点上面就能搜索到问题的全局最优解.基于这种思想，设计一种快速极点算法，具体步骤描述如下：

第1步:求出二层线性规划约束集合S的所有极点(xi,yi),i=1,2,…,n，不妨假设对于任意(xp,yp)和(xq,yq)，满足p

第2步:给定问题一个初始解(xi,yi)，i=1，i≤n，转第3步；

第3步:把xi带入下层目标函数f(x,y)，求解f(xi,y)在约束集S中的最优解yi+1，转第4步；

第4步:比较yi+1和yi值，如果yi+1=yi，停止计算，输出全局最优解(xi,yi)；否则令i=i+1，转第3步.

3数值实验

例1

s.t.y+2x≤12

2y-3x≥-4

y-2x≤0

很容易，能得到约束域S如图1所示.

图1　约束域

4小结

因为二层线性规划问题反馈最优解集的非凸性，给求解二层线性规划问题带来了一定困难，此处给出的求解二层规划全局最优解的方法，简单易行，并且具有一定的应用价值.针对极点的重新排序，相对随机取初始迭代点，此方法能更快的找到全局最优解，最后的算例验证了算法的有效性.

参考文献：

[1] BENSION H P. On the Structure and Properities of a Linear Multilevel Programming Problem[J]. Journal of Operation Theory and Applications，1989(60):353-373

[2] BEREANU B. Stable Stochastic Linear Programs and Applications[J]. Mathematischen Operation for Schung and Statistik,1975,6(4):593-607

[3] BIALAS W F,KARWAN M H. Two-level Linear Programming[J]. Managenment Science,1984,30(8):1004-1020

[4] CANDLER W，Norton R. Mulilevel Programming and Development Policy[R]. Technical Report 258，World Bank Staff，Washington DC,1977

[5] CANDLER W， TOWNSLEY R. A Linear Two-level Programming Problem[J]. Computers and Operations Research,1982,9(1):59-76

[6] BARD,J F. An Investigation of the Linear Three Level Programming Problem[J]. IEEE Transaction System,Man and Cybernetics,1984,14(5):711-717

[7] BRACKEN J，MCGILL J T. Mathematical Programs with Optimization Problems in the Constraints[J]. Operation Research，1973,21(1):37-44

[8] 陶玉洁，张永，杨杰.二层线性规划求顶点的算法[J].通化师范学院学报，2007，28(4):8-10

[9] 胡长英.双层规划理论及其在管理中的应用[M].北京：知识产权出版社，2012

[10] 李宏卫，王军.三次型非线性包装系统跌落冲击响应分析[J].包装工程：工程版，2015(19)：18-22

The Method of Getting Extreme Point of the Optimal Solution toBilevel Linear Programming

ZHAO Li-yang1,HUO Yong-liang2

(1.School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China; 2.School of

Mathematics and Finance,Chongqing University of Arts and Sciences,Chongqing 402160,China )

Abstract：According to the theory that the optimal solution to bilevel linear programming can be found on the extreme point of the constraint set,a method of getting extreme point of bilevel linear programming is presented. Through the top objective function sorting,this method avoids the shortcoming of verifing extreme point aimlessly. Finally,calculation example describles the perocess of algorithm for solving,and the effectiveness of the algorithm is verified.

Key words： bilevel linear programming; constraint condition; globle optimal solution; exeme point