基于傅立叶级数的半参数CAViaR模型的贝叶斯分析

基于傅立叶级数的半参数CAViaR模型的贝叶斯分析*

曾惠芳1， 熊培银2

(1.湖南科技大学 商学院，湖南 湘潭 411201； 2.湖南科技大学 信息与电气工程学院，湖南 湘潭 411201)

摘要：针对金融市场复杂性及不确定性，为了更灵活地测度金融市场的波动风险，提出了一类半参数CAViaR模型，利用傅立叶级数拟合前一期信息对当前VaR风险值的非线性影响，选择合适的先验分布，基于非对称Laplace分布构建了相应的似然函数，推导了参数的后验分布，从而实现了对CAViaR模型的贝叶斯推断；最后利用贝叶斯CAViaR模型研究了上海综合指数的风险波动特征，结果发现上证综指的风险波动存在自回归性.

关键词：贝叶斯分析；傅立叶级数；半参数方法；CAViaR模型

doi:10.16055/j.issn.1672-058X.2015.0011.003

收稿日期：2015-05-20；修回日期：2015-07-20.

基金项目：*国家自然科学

作者简介：曾惠芳(1981-)，女，湖南省邵阳人，讲师，博士，从事贝叶斯空间统计研究.

中图分类号：F224.9；O212文献标志码：A

随着经济全球化及投资自由化，全球范围内，汇率、利率、股票价格和商品价格高度波动，呈现不断加剧的趋势.这些基础市场价格因子的高度波动，直接反映为金融市场风险的不断增大.自20世纪90年代以来，国际金融市场经历了一些重大的结构性变化，对金融市场风险产生了更为深远且深刻的影响.它们大大增加了金融市场和工具的关联度、复杂性、不确定性和波动性，使得金融市场风险上升，结构成分复杂，难以测量分析.

由于金融资产价格行为的复杂性，度量金融风险的方法越来越多，其中利用分位回归方法度量金融风险是目前研究的热点.分位回归方法不对金融时间序列的分布做任何假设，为有效地度量金融风险提供了一种灵活的方法.Taylor(1999)提出利用分位回归模型估计多期风险值的情形，并研究德国马克、英镑与日元汇率，发现分位回归模型用于估计多期风险值有良好的表现；Engle和Manganelli(2004)提出了非线性动态VaR模型(CAViaR)，CAViaR模型只描述条件分布尾部的行为，不受异常点的影响；刘新华，黄大山(2005)采用Hansen检验方法讨论了中国股市风险CAViaR建模的稳定性问题；张颖和孙和风(2012)提出了一类包含信息不对称性的GJR-CAViaR模型，并把它应用于刻画中美股票市场风险的差异；闫昌荣(2012)提出了一类流动性调整CAViaR模型，并计算了资产未来经过流动性调整的风险VaR；王新宇等(2010)考虑到金融资产收益与正负收益对分位数冲击的不对称性，建立含有不对称绝对值和斜率设定的AAVS-CAViaR模型，对1996-2008年期间沪深港股票指数进行了实证研究；王新宇等(2013)提出了带有结构变点的条件分位数自回归模型，利用非对称拉普拉斯分布实现了模型的贝叶斯推断.此处将基于傅立叶级数构建一类半参数CAViaR模型，并实现对模型的贝叶斯推断，最后把贝叶斯CAViaR模型应用于中国股票市场的风险测度，发现中国股票市场的VaR风险存在自相关性.

1模型结构分析

Engle和Manganelli(2004)提出了4种CAViaR模型，分别是自适应CAViaR，对称CAViaR，非对称CAViaR，GARCH(1,1)-CAViaR模型.实际上，金融市场收益率的波动特征更丰富，而且Engle和Ng(1993)曾经也提出了利用非参数方法，即线性样条方法，估计滞后收益率对波动率的影响.此处将提出一类新的更灵活的模型来度量VaR风险，即半参数CAViaR模型：

(1)

(2)

其中，

为简便起见，可利用式(2)中的前k项近似g(yt-1)，并记Θ=(θ11，…，θk),这样可以通过解如下最优化问题来实现模型的估计

(3)

其中ρτ(u)=u(τ-I(u<0)).因为分位回归估计最小化问题可以等价于以非对称Laplace分布为似然函数的极大似然估计问题，因此似然函数可以表示为

(4)

其估计量可以看作是分位回归模型的伪极大似然估计,其中Y=(y1,…,yn).

为了实现模型的贝叶斯估计，首先给出参数的先验分布.因为对函数g进行平滑时会依赖于分位数τ，一般在极值分位水平下，数据比较少，需要较大的光滑.因此可以设计参数g的先验分布为

其中,

(5)

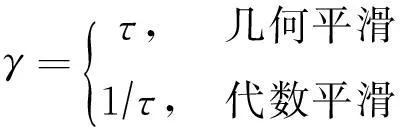
(6)

式(6)可以保证傅立叶级数以概率收敛于被拟合的函数.从式(5)来看，傅立叶级数系数的先验分布的方差有两种形式.代数平滑器平滑程度集中于γ的函数，而几何平滑器先验平滑程度由解析函数控制.参数δ2控制着未知函数g的全局不确定性，即用于确定先验分布和似然函数之间的平衡关系.参数γ确定了傅立叶系数的衰减速度，因此能起到对函数g平滑的作用.显然，其他基函数以及先验分布可以用于模拟函数g,并且假设δ2独立于{θk}，其先验分布为服从参数为r02，s02的逆伽玛分布，可以表示为

2模型的贝叶斯推断

以非对称Laplace分布为基础的非参数分位回归模型的贝叶斯推断很难得到傅立叶系数的解析后验分布，即无法得到解析的后验均值和后验方差，以及无法得到参数解析的完全条件分布，不能用Gibbs抽样来实现对模型的模拟，引入标准指数分布和标准正态分布的混合分布，从而可以得到模型参数解析的完全条件分布，实现模型的Gibbs抽样.

假设z服从标准指数分布，u服从标准正态分布,如果变量ε服从非对称Laplace分布，其密度函数表示为

那么ε可以表示为

其中φ=(1-2τ)τ(1-τ)，ω2=2τ(1-τ).这样，半参数CAViaR模型可以表示为

(7)

为了简便起见，式(7)可以表示为

(8)

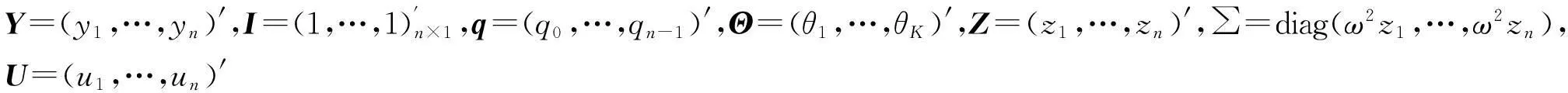
这样，在一定的条件下Y条件分布可以表示为以β0I+β1q+ΦΘ+φZ为均值，以∑为方差的正态分布，因此Y的联合分布可以表示为

(9)

3实证分析

图1　上证综指周收益率的 波动轨迹

金融风险的度量方法有很多，要建立一个金融风险的测度机制，研究金融市场的动态特征非常重要.迄今为止，描述金融市场动态特征的模型当首推广义自回归条件异方差模型(GARCH).为了研究上证综指周数据的风险值，样本选择的时间段为2006年1月到2011年2月.图1给出了周收益率的波动轨迹.

2008年的全球金融危机对中国经济也产生了巨大的影响.在度量中国股票市场的风险时，金融危机对中国股市的影响不容忽视.为了更灵活地度量中国股票市场的风险，此处将采用半参数CAViaR模型来度量中国股票市场的风险,利用三阶傅立叶级数拟合模型中的非参数部分，用一条马尔可夫链模拟模型参数的后验分布，将最初的4 000次迭代得到的样本舍去，用第4 001次到第10 000次迭代得到6 000个模拟样本去估计模型参数.图2给出了模型参数的后验分布核密度函数.图2密度曲线表现比较平滑且呈钟型，说明MCMC(MarkovChainMonteCarlo)算法有效地模拟了模型中各参数的边缘后验分布.表1给出了半参数CAViaR模型参数的后验均值、标准方差、蒙特卡罗误差和贝叶斯置信区间.

图2　参数的后验核密度函数

参 数均 值标准差MC误差0.025分位数0.975分位数α(0.5)0.46530.11740.01400.2700.720θ1(0.5)-9.92903.2300.2960-17.06-3.755θ2(0.5)11.06005.5550.50300.25922.570θ3(0.5)-13.92004.1400.3845-22.920-5.842α(0.9)-0.01430.49690.0468-0.7960.872θ1(0.9)42.84018.3301.5294.99472.620θ2(0.9)-20.62012.5801.008-42.0904.679θ3(0.9)9.1406.9390.5075-4.49422.29

根据表1可知，在分位水平τ=0.5时，参数部分自回归系数α后验均值的估计为0.465 3，95%置信区间为(0.270，0.72)；非参数部分傅立叶级数θ1后验均值的估计为-9.929，95%置信区间为(-17.06，-3.755)；θ2后验均值的估计为11.06，95%置信区间为(0.256，22.57)，θ3后验均值的估计为-13.92，95%置信区间为(-22.92，-5.842).在分位水平τ=0.9时，参数部分自回归系数α后验均值的估计为-0.014 3，95%置信区间为(-0.796，0.872)；非参数部分傅立叶级数θ1后验均值的估计为42.84，95%置信区间为(4.994，72.62)；θ2后验均值的估计为-20.62，95%置信区间为(-42.09，4.679)，θ3后验均值的估计为9.14，95%置信区间为(-4.494，22.29).从结果可以看出，VaR过程存在自回归过程，即滞后一阶的风险对目前的风险会有影响，同时，滞后一阶的冲击对当前的风险也存在非线性的影响.

4结论

提出了一类基于傅立叶级数的半参数CAViaR模型，并给出了模型的贝叶斯推断和MCMC抽样估计算法，对于灵活地测度金融市场的VaR风险值具有重要的意义.把贝叶斯半参数CAViaR模型应用于中国股票市场的风险测度，结果发现中国股票市场的VaR风险存在自相关性和羊群效应.但是，如何把极值理论与非参数方法结合起来估计金融风险值是未来研究的方向.

参考文献：

[1] TAYLOR J W.A Quantile Regression Approach to Estimating the Distribution of Multiperiod Returns[J].Journal of Derivatives，1999(7)：64-78

[2] ENGLE R，MANGANELLI S.Conditional Autoregressive Value at Risk by Regression Quantiles[J].Journal of Business & Economic Statistics，2004(22):367-381

[3] 刘新华，黄大山.中国股市风险CAViaR方法的稳定性分析及其时变建模[J].系统工程理论与实践，2005(3):1-6

[4] 王新宇，宋学锋.间接TARCH-CAViaR模型及其MCMC参数估计与应用[J].系统工程理论与实践，2008,28(9)：46-51

[5] 叶五一,缪柏其,谭常春.基于分位点回归模型变点检测的金融传染分析[J].数量经济技术经济研究,2007(10):151-160

[6] 王新宇，赵绍娟.基于分位数回归模型的沪深股市风险测量研究[J].中国矿业大学,2008,37(3):416-421

[7] 关静,史道济.分位数回归与上证综指VaR研究[J].统计与信息论坛，2008，23(12):15-19

[8] 钱争鸣，郭鹏飞.上海证券交易市场量价关系的分位回归分析[J].数量经济技术经济研，2007(10):141-150

[9] KUESTER K，MITTIK S，PAOLELLA M S.Value-at-risk Prediction：A Comparison of Alternative Strategies[J].Journal of Financial Econometrics，2005，4(1):53-89

[10] 张颖，孙和风.中美股票市场风险差异的新解释——收益对市场风险不对称效应的CAViaR模型与实证[J].南开经济研究，2012(5)：111-120

[11] 闫昌荣.基于流动性调整CAViaR模型的风险度量方法[J].数量经济技术经济研究，2012(3)：131-140

[12] 王新宇，宋学峰，吴瑞明.基于AAVS-CAViaR模型的股市风险测量研究[J].系统工程学报，2010,25(3):326-333

[13] 王新宇，吴祝武，宋学锋．变点CAViaR市场风险测量模型及创业板应用[J].中国矿业大学学报，2013,42(3):506-512

Bayesian Analysis of Semi-parametric CAViaR Model Based on Fourier Series

ZENG Hui-fang1， XIONG Pei-gen2

(1.Business School，Hunan University of Science and Technology，Hunan Xiangtan 411201，China; 2.School of

Information and Electrical Engineering，Hunan University of Science and Technology，Hunan Xiangtan 411201，China)

Abstract：According to the complexity and uncertainty in financial market，in order to more flexibly measure the volatility risk of financial market，this paper presents a class of semi-parametric CAViaR model by using the non-linear influence of former term fitting information of Fourier series on current VaR risk value to select suitable priori distribution，the related likelihood function is constructed based on asymmetric Laplace distribution，the posterior distribution of the parameters is deduced，and thus，the Bayesian deduction for CAViaR model is implemented.Finally，the feature of the risk volatility of Shanghai Composite Index is studied based on Bayesian CAViaR model and its results show the risk volatility of Shanghai Composite Index has auto-regression.

Key words： Bayesian analysis; Fourier series; semi-parametric method; CAViaR model