广义Burgers-BBM方程波前解的持续性

广义Burgers-BBM方程波前解的持续性*

崔中飞， 傅仰耿

(华侨大学 数学科学学院，福建 泉州 362021)

摘要：对广义Burgers-BBM方程的波前解进行研究，在黏性充分小的情况下，运用几何奇异摄动理论证明其波前解是持续的.

关键词：广义Burgers-BBM方程；波前解；几何奇异摄动理论；持续性

doi:10.16055/j.issn.1672-058X.2015.0011.002

收稿日期：2015-05-04；修回日期：2015-06-10.

基金项目：*国家自然科学基金资助(11401229).

作者简介：崔中飞(1991-)，男，硕士研究生，从事微分方程与动力系统研究.

中图分类号：O157.2文献标志码：A

1基础知识

利用几何奇异摄动理论研究广义Burgers-BBM方程：

(1)

波前解的持续性，其中μ，δ和ε为正常数，分别刻画耗散、色散和黏性的效果.当ε=0时，方程(1)即为Burgers-BBM方程：

(2)

它可以看成是Burgers型方程与BBM方程所组合的简单扩散模型，可以描述非线性色散介质中单向传播的水波[1]和流体力学中具有有限的小振幅水波[2]等.当μ=0时，方程(2)变为BBM方程：

(3)

式(3)是Benjamin-Bona-Mahony于1972年在水波研究中提出的[2]，其中δ是色散系数，它可以用来描述冷等离子体中的水磁波、可压缩流体中的声重力波、和谐水晶中的声波[3]等.在这些物理现象的研究中，方程行波解的研究起到重要的作用.因为不管是精确的还是数值的行波解，都可能对理解这些物理现象提供更多的信息.目前对方程(2)的解法主要有正切函数法[5]、Fourior解法[6]、吴方法[7]等.通过这些方法，也找到一些精确波前解.1992年，张卫国和王明亮利用待定系数法分别求出了方程(2)的一类指数函数有理分式形式的精确波前解

并且证明了方程(2)的这类行波解可分解为Burgers方程的行波解和BBM方程的行波解的线性组合[8].2009年，姜璐利用首次积分法得到了方程(2)的两种形式的精确波前解[9]：

波前解的存在性问题是行波理论的一个基本问题.由于非线性波方程的波前解实际上对应相应行波系统的异宿轨，故波前解存在性的研究通常转化为相空间上异宿轨存在性的研究.然而当非线性波方程所对应行波系统的相空间是高维时，异宿轨的存在性就会变得非常困难.因此利用几何奇异摄动理论[10]研究小参数情况下非线性波方程波前解的持续性已经成为一个重要方向.例如KBK方程波前解的持续性[11]、含有时空延迟的KPP方程的波前解的持续性[12]、疾病模型中行波解的存在性[13]等.

下面将从动力系统和几何奇异摄动理论的角度来探讨当ε充分小时，方程(1)的波前解的持续性.

2动力系统的刻画

式(1)做行波变换，将u(x，t)=u(ξ)，其中ξ=x-ct代入式(1)，得

(4)

积分式(4)一次，得

(5)

(6)

显然系统(6)有下面两个平衡点

系统(6)在Y0的Jacobi矩阵为

其对应的特征方程为

(7)

类似地，系统(6)在Y1的Jacobi矩阵为

其对应的特征方程为

(8)

从而有下面的结论：

证明定理的证明主要依据辐角原理.Y0线性化的谱是由式(7)决定的，令

则式(7)可以改写成m0(λ)=0.下面证明m0(λ)=0在右半复平面上只有一个根.由于m0(λ)是解析的，故式(7)在右半复平面上根的个数为

(9)

其中周线C0是以原点为圆心、以R为半径的落在右半复平面内的半圆与虚轴所组成的有向围线，其方向是逆时针方向；ΔC0argm0(λ)表示m0(λ)沿着C0总的辐角改变量.式(9)等于

其中中括号里的量表示当R从+∞到-∞时m0(iR)的总辐角改变量.因此需要计算m0(iR)的象绕着原点转了几圈.注意到

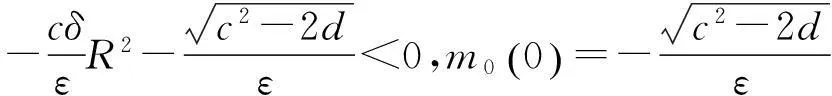
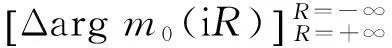
类似地，令

则式(8)可以改写成m1(λ)=0.同理可得式(8)在左半复平面上根的个数是

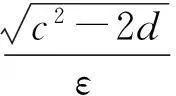
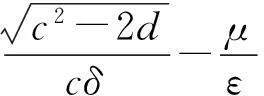
3波前解的存在性

如果Burgers-BBM方程存在一个单调增加的波前解，那么将证明对于充分小的ε，广义Burgers-BBM方程也存在一个波前解.当0<ε<1时，系统(6)可以改写成

(10)

系统(10)通常被称为“慢系统”，其对应的“快系统”为

(11)

若在系统(10)中令ε=0，则u，v满足系统

(12)

且w属于集合

其中M0是R3的一个二维子流形.

根据文献[10]中的定义，流形M0被称为是正规双曲的，如果快系统限制在M0上，有M0维数个特征值在虚轴上，且剩下的都是双曲的，则快系统(11)限制在M0上的线性化系统的矩阵为

因为矩阵A的特征值是0，0，-cδ，所以流形M0是正规双曲的.因此，由Fenichel不变流形理论知，对充分小的ε>0，存在R3的一个二维子流形Mε包含于M0的O(ε)领域内，并与M0是微分同胚的.

为了确定Mε上的动力学行为，记

(13)

其中h光滑地依赖于ε且h(u，v，0)=0.将式(13)中的w的表达式代入系统(10)的第3个方程，得

(14)

将h展成ε的泰勒级数

然后代入式(14)并比较ε的同次幂系数.比较零次幂系数，得h(u，v，0)=0；比较一次幂系数，得

这样就可以改写系统(10)为

(15)

系统(15)决定Mε上的动力学行为.下面给出并证明持续性定理.

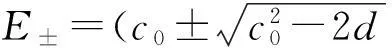
把系统(15)改写为

其中Φ(u，v，c，ε)满足

因为u0(ξ)是严格增加的，故可以被刻画成某个函数的图像，把这个函数表示成

v=f(u，c0)

根据稳定流形定理，对于充分小的ε，Wu(E-)可以被刻画成函数

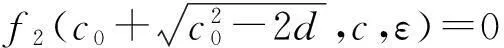
为了证明当ε充分小时，系统(15)存在一条异宿轨，只需证明在c0附近存在唯一的c(ε)，使得流形f1和f2相交与直线u=c0上的同一点.令

由于v=f1(u，c，ε)和v=f2(u，c，ε)都满足方程

(16)

可以得

(17)

命令

由于

解式(17)得

这样就有

类似地有

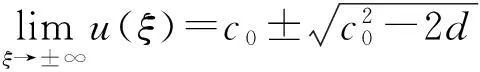
参考文献：

[1] 聂世丽，贾有见.利用指数函数法解Burgers-BBM方程[J].科学技术与工程，2011，11(21)：1671-1815

[2] 徐红梅，吴笑天.BBM-Burgers方程解的衰减估计[J].数学杂志，2014，34(4)：723-728

[3] BENJAMIN T B，BONA J L，MAHONY J J.Model Equation for Long Water Waves in Nonlinear Dispersive Systems[J].Philos Trans R Soc London Series A，1972(272)：47-78

[4] SEADAWY A R，SAYED A .Travelling Waves Solutions of the Benjamin- Bona -Mahonye Water Wave Equations[J].Abstract and Applied Analysis，2014(293)：57-66

[5] 张金良，王跃明，王明亮.两类非线性方程的精确解[J].物理学报，2003，52(7)：1575-1578

[6] 龚伦训.修正的BBM方程的一些新的精确解[J].原子与分子物理学报，2006，23(4)：527-728

[7] 苏道毕力格，朝鲁.用吴方法计算Burgers-BBM方程的势对称及其不变解[J].内蒙古大学学报，2006，37(4)：366-373

[8] 张卫国，王明亮.B-BBM方程的一类准确行波解及结构[J].数学物理学报，1992，12(3)：325-331

[9] 姜璐.Burgers-BBM方程新的精确解[J].南昌工程学院学报，2009，28(1)：41-46

[10] FENICHEL N.Geometric Singular Perturbation Theory for Ordinary Differential Equation[J].Differential Eqs，1979(31)：53-98

[11] YANG G F，ZHEN G L.Persistence of Travelling Fronts of KdV-burgers-kuramoto Equation[J].Applied Mathematics and Computation，2010(216)：2199-2206

[12] ASHWIN P，BARTUCCELLI M，BRIDGES T.Travelling Fronts for the KPP Equation with Spatio-temporal Delay[J].Math Phys，2012(53)：103-122

[13] RUAN S，XIAO D.Stability of Steady States and Existence of Travelling Waves in a Vector-disease Model[J].Proc Roy Soc Edinburgh Sect A，2004(134)：991-1011

Persistence of Travelling Fronts of Generalized Burgers-BBM Equation

CUI Zhong-fei， FU Yang-geng

(School of Mathematical Sciences，Huaqiao University，Fujuan Quanzhou 362021，China)

Abstract：By geometric singular perturbation theory，this paper proves that travelling fronts of the Generalized Burgers-BBM equation persist under the condition of sufficiently small viscosity.

Key words： the generalized Burgers-BBM equation；wave-front solution；geometric singular perturbation theory；persistence