含单侧预制裂纹梁的冲击动态断裂过程试验研究

第一作者 李清 男，教授，1969年生

通信作者 张迪 男，博士，1987年生

邮箱：540375465@qq.com

含单侧预制裂纹梁的冲击动态断裂过程试验研究

李清，张迪，杨阳，郝建伟，薛耀东，王强勋，李进宇

(中国矿业大学 力学与建筑工程学院，北京100083)

摘要：利用动焦散线试验方法研究了冲击下预制裂纹梁的动态断裂行为，对比分析了冲击荷载作用下单裂纹与双裂纹试件的应力强度因子、扩展轨迹以及速度、加速度等参数的变化规律。试验结果表明：冲击荷载作用下，含双裂纹且主裂纹在冲击点正下方的试件起裂时间最早，裂纹扩展后期朝向次裂纹方向发生较小的偏移；含Ⅰ型单裂纹的试件起裂时间次之，裂纹扩展路径呈直线；含双裂纹且两条裂纹均偏置于冲击点的试件起裂时间最晚，扩展过程中发生明显的曲裂现象。同时，裂纹扩展过程中曲裂现象越严重，裂纹扩展的最大速度就越小。在落锤冲击试件到试件断裂的整个阶段，应力强度因子一直表现出振荡变化。含双裂纹的试件，在主裂纹扩展中期，次裂纹上的应力强度因子有一个快速下降的过程。

关键词：预制裂纹；冲击荷载；裂纹扩展；动焦散线

基金项目：国家自然科学基金资助项目(51374212，51134025)

收稿日期：2013-10-09修改稿收到日期：2014-02-20

中图分类号:O348.1文献标志码： A

Dynamic fracture tests for a beam containing unilateral pre-existing cracks under impact loads

LIQing,ZHANGDi,YANGYang,HAOJian-wei,XUEYao-dong,WANGQiang-xun,LIJin-yu(School of Mechanics and Architecture Engineering，China University of Mining & Technology，Beijing 100083, China)

Abstract:By means of experimental method of dynamic caustics, the dynamic fracture behaviors, such as, stress intensity factor, extension track, and crack’s extending velocity and acceleration of precast beams with a single crack and double cracks under impact loads were analyzed comparatively. The experiment results indicated that when the impact point is directly upon the main crack, the double-crack beam’s cracking initiation time is the earliest with a extension track of the main crack slightly offsetting to the secondary crack in the late stage of cracking extension; the single-crack beam of I-type’s cracking initiation time is secondary with a straight line extension track of the main crack; the cracking initiation time of the double-crack beam with two cracks offset to the impact point is the latest with obvious bending fracture; the more serious the bending fracture phenomenon during the process of crack extension, the smaller the maximum extending velocity; in the whole process from the hammer contacting the beams to specimens fracture, their stress intensity factors vary oscillatorily; the stress intensity factors of the secondary crack of the double-crack beam decrease dramatically in the middle stage of the main crack extending.

Key words: pre-existing crack; impact loading; crack propagation; dynamic caustics

梁有着广泛的工程应用，大部分梁结构经常处于冲击荷载的作用下，而含缺陷的梁的动态断裂行为与在静态断裂的情况下有很大的差别[1-4]，这一直是研究的热点。由于裂纹在扩展过程中存在着惯性力，导致裂纹尖端的力学行为十分复杂，单纯的理论计算结果和实际问题相差甚大。而试验的方法可以客观的反映材料的实际断裂过程，在研究断裂动力学方面仍发挥着重要作用而被广泛采用。

焦散线的试验方法是研究裂纹尖端奇异应力场的有效手段，只需测量出裂纹尖端的焦散斑直径，就能确定相应的应力强度因子，且测量精度较高，因此常被用于确定裂纹尖端的断裂力学参量随载荷和时间的变化规律。肖同社等[5]模拟了含节理岩体的断裂爆破过程，研究了爆炸初始裂纹与节理面不同夹角的情况下，裂纹的扩展规律。岳中文等[6]进行了爆炸应力波作用下的缺陷介质裂纹扩展试验，研究了含与炮孔共线的预制裂纹尖端的应力强度因子、动态能量释放率和速度等的变化规律。励争等[7]研究了PP/PA6/POE-g-MA共聚物的静、动态力学性能，采用反射型焦散线方法对其动态断裂性能进行了研究，并进一步分析其材料损伤破坏机理。杨仁树等[8]进行了爆炸加载下的透射式动焦散试验，研究了闭合和张开节理对切缝药包的断裂控制爆破裂纹扩展规律的影响和裂纹扩展机制。试验中常用三点弯曲梁来研究Ⅰ型或Ⅰ型、Ⅱ型复合型裂纹的扩展问题，而利用动焦散线的试验方法，能精确的观测到三点弯曲梁中裂纹的起裂和扩展过程。边亚东等[9]对比分析了冲击下预制裂纹梁中Ⅰ型裂纹与偏置裂纹的裂纹扩展差异。刘宁等[10]对碳纤维布加固含裂纹梁进行了三点弯荷载下的静态和动态焦散线实验，研究了其断裂特性。姚学锋[11]等利用动态焦散线研究了含裂纹的三点弯曲梁在冲击下扩展裂纹尖端的动态能量释放率的分布规律。

通过利用动态焦散线方法，对含预制裂纹的梁试件在冲击下的动态断裂行为进行了研究。对比分析了Ⅰ型双裂纹试件与单裂纹试件受到冲击后的应力强度因子、扩展轨迹以及速度、加速度等参数的差异，以及偏置双裂纹试件的断裂机理。

1动态焦散线的实验原理与实验装置

1.1裂纹冲击动态断裂力学参数的确定

(1) 确定裂纹动态应力强度因子

冲击荷载下在梁内形成了自加载点向周围扩散的应力波，试件A的裂纹受正应力作用，裂纹扩展为Ⅰ型断裂；试件B、试件C裂纹尖端受剪应力和正应力的共同作用，裂纹扩展为Ⅰ、Ⅱ复合型断裂。冲击作用下裂纹动态应力强度因子的计算公式[12]：

(1)

KⅡ=μKΙ

(2)

式(1)和式(2)中：KⅠ、KⅡ为Ⅰ型、Ⅱ型裂纹动态强度因子；F(v)是裂纹扩展速度的修正因子，实际计算中取F(v)≈1；z为参考面到物体平面的距离；c为透射动焦散线应力光学常数；deff为透明材料实际厚度；Dmax为沿裂纹方向的焦散斑的最大直径；μ为应力强度因子比例系数。g为应力强度因子数值，由μ确定；在试验条件确定的情况下，z、c和deff都是常数。

(2) 确定裂纹扩展速度、加速度

由焦散斑特征长度的定义，裂纹尖端距离焦散斑前沿的距离D为

(3)

式中：Dt为焦散斑的纵向直径。由动焦散线图片确定相邻两个时刻的裂纹尖端扩展距离，并与式(3)得到的距离D相加，即可确定最终的裂纹长度b及相应的水平和垂直位移分量X、Y。将X、Y拟合为t的4次多项式，表达式为

(4)

式中：an、bn是裂纹扩展形状参数，由最小二乘法求得。

为了减少误差，分别求X、Y对时间t的一阶和二阶导数，进一步将它们加以合成，得到不同瞬时裂纹扩展的速度v和加速度a：

(5)

(6)

1.2试验装置

采用DDGS-Ⅱ多火花式高速摄影光路系统，实验光路系统是由多火花式高速相机与双场镜组成，一端是4×4方阵的16个放电器，另一端是4×4方阵的16个镜头组成的照相机，当16个放电器按设置的延迟时间与幅间间隔放出电火花时，16个相机镜头便分别记录了16个不同瞬时的图像(见图1)。

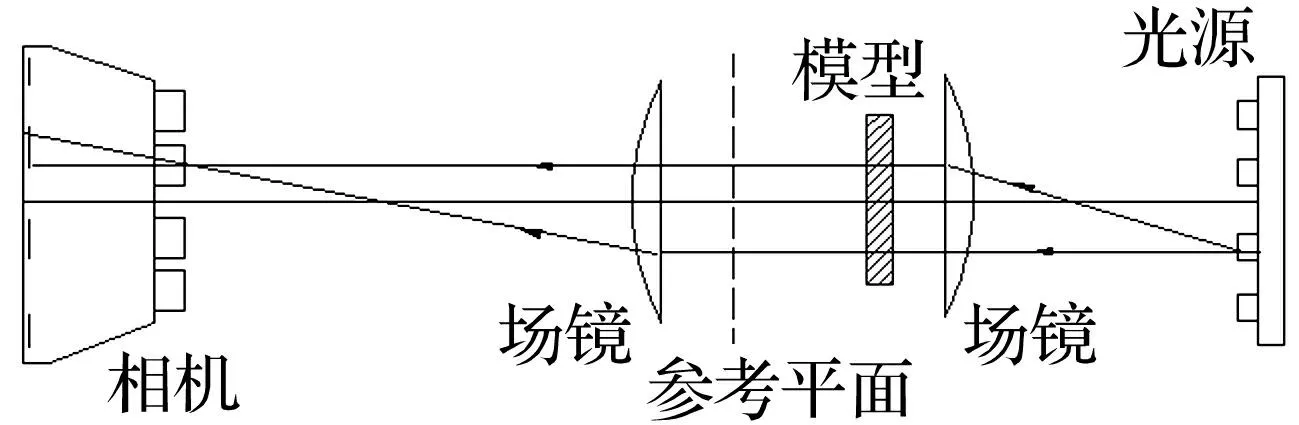
图1　透射式动焦散线试验系统 Fig.1 Experimental system for dynamic caustics

1.3试验描述

图2　冲击载荷下含 预制裂纹试件实验装置 Fig.2 Experimental device forpre-existing crack unit under impact loading

试验采用落锤冲击加载，落锤重量及下落高度可调范围较大，落锤冲击时接触时间一般在100～200 μs之间。试件与参考平面之间的距离z为700 mm，落锤重量2 kg，下落高度340 mm, 加载速度2.58 m/s(见图2)。

实验材料为有机玻璃板，规格为210 mm×40 mm×5 mm，裂纹宽度控制在0.3 mm以下，设计裂纹长度为8 mm，图3为试件A、B、C的三点弯曲梁尺寸、裂纹所在位置示意图，其中试件A为单裂纹，试件B、试件C都是双裂纹。

图3　三点弯曲梁模型 (mm) Fig.3 Three-point bending beam model

对试验中采用的有机玻璃的动态力学光学参数进行了测定，具体数值见表1。

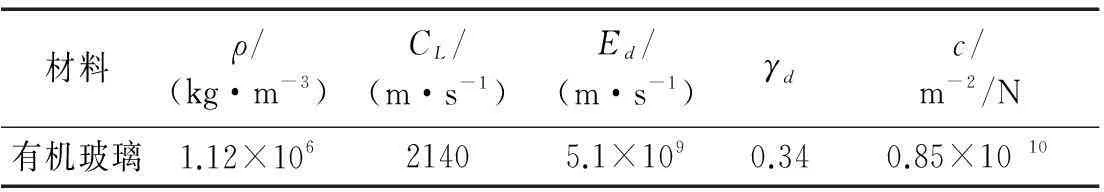
表1　模型材料的动态力学光学常数

注：CL为纵波波速；Ed为动态弹性模量；d为动态泊松比；c为动态应力光学参数常量。

2预制裂纹梁冲击断裂力学特征试验分析

2.1试验结果

为与实际工程情况相类似，对含预制裂纹的有机玻璃梁试件采用半固端约束。在这里将试件B、试件C发生开裂扩展的裂纹叫做主裂纹，没有发生开裂破坏的裂纹叫做次裂纹。试件破坏效果(见图4)。试件A的裂纹扩展路径呈直线；试件B的主裂纹在扩展后期朝向次裂纹方向发生偏转；试件C的预制裂纹偏置，扩展过程中发生明显的曲裂现象。

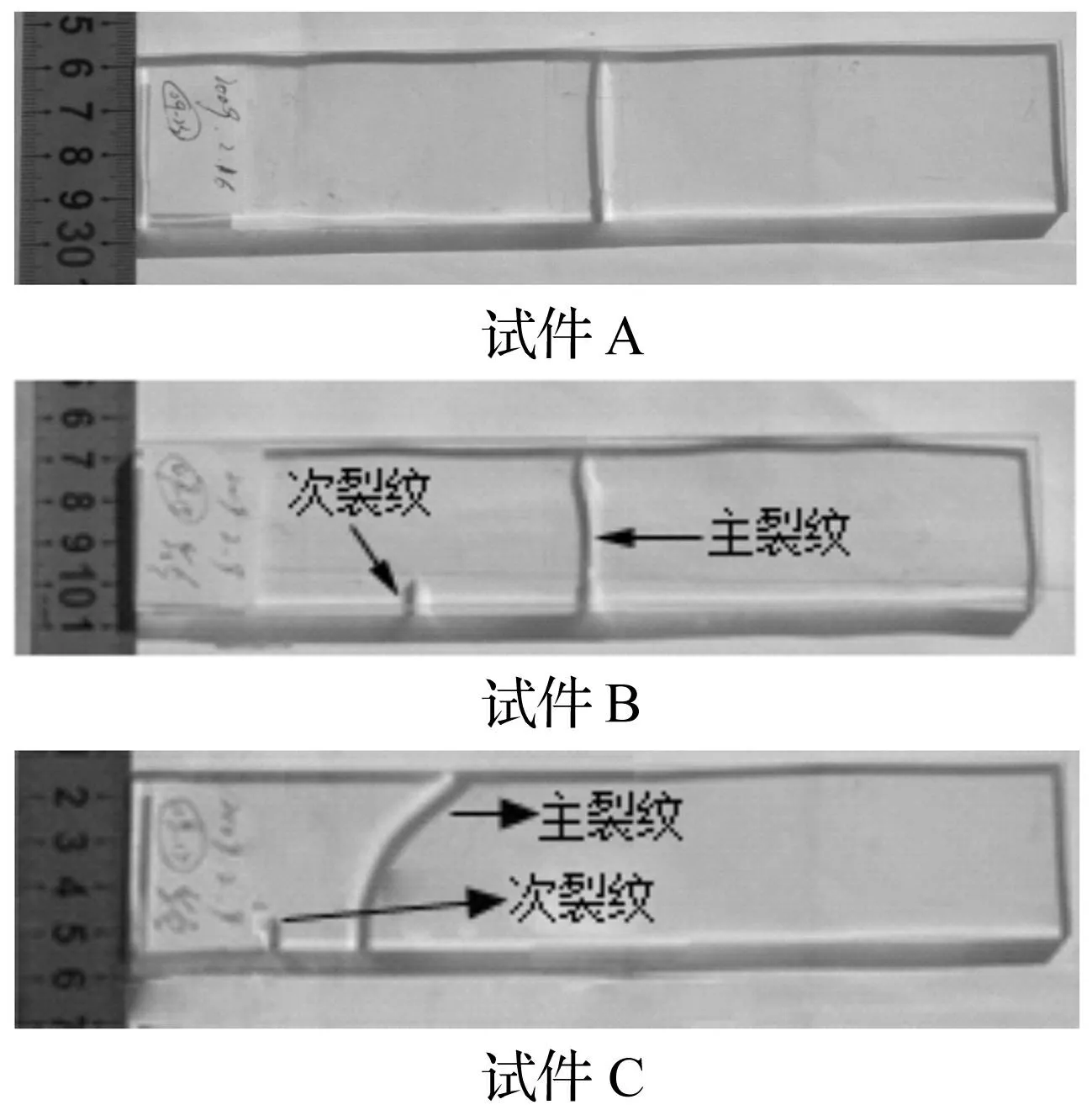
图4　三点弯曲梁断裂效果图 Fig.4 Fracture pictures of Three-point bending beam

图5分别给出了三种试件的裂纹尖端扩展过程的动焦散线扫描图像。从高速摄影系统拍摄到的有效照片中观察到，受到落锤冲击一段时间后，三种试件的裂纹尖端都出现了焦散斑，并逐渐变大；裂纹开裂后，从焦散斑的移动可以清晰的观测到裂纹尖端的扩展运动。不同于试件A，试件B、试件C是双预制裂纹，在主裂纹出现焦散斑后的很短时间，次裂纹尖端也出现了焦散斑；随着主裂纹的开裂扩展，次裂纹处的焦散斑在主裂纹扩展中期有一个迅速减小的过程；裂纹扩展后期，主、次裂纹的焦散斑均逐渐变小，直至裂纹贯穿试件，焦散斑消失。冲击载荷产生的应力波开始在试件内部传播时，首先会到达距离加载点较近的主裂纹尖端，一段时间后才到达距离较远的次裂纹处，这即是主裂纹先于次裂纹出现焦散斑的原因。随着应力波在裂纹与试件边界的多次反射并相互叠加，主裂纹尖端的能量积聚不断增大，观察到的焦散斑逐渐增大，直至裂纹起裂、扩展；同时，次裂纹处的裂纹尖端也在积聚能量，表现为焦散斑也同时在逐渐变大，但次裂纹尖端积聚的能量不足以引起裂纹起裂，仅造成了裂纹尖端处的破坏。

图5　预制裂纹三点弯曲梁动焦散线图像(部分) Fig.5 Dynamic caustics of three-point bending beam with pre-existing crack

2.2裂纹扩展轨迹分析

图6是三种试件裂纹扩展轨迹和方向角与时间的关系曲线。由于试件B比A多了一条预制裂纹，裂纹在起裂与扩展的过程中表现出了差异性。从图6中观察到，试件B的主裂纹(350 μs)先于试件A(371 μs)开裂，开裂后，两种试件的裂纹的垂直位移分量迅速增加；试件B的主裂纹在扩展后期(431～449 μs)朝向次裂纹方向发生约4°的偏移，随后沿着偏移的方向继续扩展至试件断裂，由于试件B的两条裂纹的距离相对较近(40 mm)，主裂纹在扩展过程中受到次裂纹的影响；而试件A的裂纹在扩展过程中没有偏移现象的发生，水平位移分量为零。

图6　裂纹尖端扩展与时间关系曲线 Fig.6 The change curves of crack tip propagation with time

试件C两条预制裂纹偏置，主裂纹在550 μs起裂后就发生了曲裂运动，但裂纹扩展初期(50 μs内)的曲裂程度较小，裂纹主要表现为垂直位移分量的增长；50～70μs，裂纹扩展方向显著偏转(偏转角从8°～24°)，发生了第一次明显的曲裂运动，水平位移分量迅速增长；裂纹扩展一段时间后(90～130 μs)，又偏离第一次的曲裂轨迹进行了第二次曲裂运动(偏转角从26°～46°)；190 μs后，裂纹又发生第三次曲裂运动，曲裂方向朝向预制裂纹初始方向，表现为图6(b)偏转角的减小(由48°≃25°)，最后与试件的上边界贯穿。

从三种试件的焦散斑形状可知，试件A的裂纹受Ⅰ型荷载作用，裂纹为Ⅰ型裂纹；试件B、试件C的裂纹受Ⅰ型、Ⅱ型复合型荷载作用，但试件B的主裂纹的荷载以Ⅰ型为主。因此，在试件A的裂纹整个扩展过程及试件B的裂纹扩展前期，裂纹尖端为张开变形，扩展方向沿预制裂纹的初始方向；而试件B由于次裂纹的存在，应力波在试件内部的传播发生了变化，改变了裂纹尖端的应力分布，裂纹受到的剪应力作用逐渐增大，最终导致了扩展方向的偏移。而试件C的两条裂纹均偏置于冲击点，主裂纹受弯矩和剪应力的共同作用，裂纹开裂后即发生偏转运动；随着裂纹的扩展，裂纹尖端的剪应力分量不断增大，曲裂程度也逐渐增加；当扩展超过试件的水平中心线时，裂纹尖端开始受到压应力作用，扩展速度明显变小，裂纹发生了第二次明显曲裂运动；之后裂纹继续扩展，裂纹上部的压应力逐渐变小，试件内部的弯矩上移，致使试件内的应力重新分布，最终导致裂纹产生了第三次曲裂，裂纹达到试件的上边界，试件贯穿。

图7　裂纹尖端扩展速度与加速度的变化曲线 Fig.7 Variation curves of crack tip propagating velocity and acceleration

试件B的裂纹先于试件A开裂，是由于应力波传播到次裂纹处时，一部分发生了反射形成了反射波，反射波与后传播来的应力波在双裂纹之间相互叠加，明显增加了裂纹间区域的应力场，加快了主裂纹尖端的能量积聚；而试件C的两条裂纹距离冲击点较远，应力波传播到主裂纹的时间相对较慢，能量积聚的时间变长，导致裂纹的开裂时间最晚。

2.3裂纹扩展速度、加速度分析

由式(4)、式(5)、式(6)来确定三种试件的裂纹扩展速度与加速度并绘制成曲线，如图7所示。

三种试件的速度与加速度的变化曲线表明，裂纹的扩展是非匀速的，表明了裂纹开裂后能量释放的不均匀性。裂纹开裂后，积聚的能量得到释放，试件A和试件B的速度迅速增大，分别在40 μs和60 μs后达到最大值347 m/s和338 m/s，之后速度逐渐减小，并伴随着振荡变化。加速度则在很短的时间内达到峰值后迅速减小，当裂纹的扩展速度达到最大值时加速度降低到零点，随后在零点附近小范围的上下波动，试件A和试件B的加速度波动幅值很接近，表明两种试件的速度变化情况大体相同。试件C的裂纹扩展过程相对较长，速度的振荡变化比试件A、试件B明显得多，扩展速度较小，最大速度仅为304 m/s。三种试件裂纹扩展的最大速度呈递减趋势，是由于扩展路径沿裂纹初始方向的距离减小，曲裂现象越来越严重。裂纹扩展主要依赖于裂纹尖端运动的惯性作用，而裂纹发生偏转时所消耗的能量比在直线路程上大得多。在试验条件相同的前提下，试件内部产生的总能量相同，用于推动裂纹扩展消耗的能量增多，从而使得裂纹扩展速度变小。

从图6与图7中还可以看出，试件C的裂纹扩展过程中，速度有三处明显的振荡变化。同时，加速度在达到峰值后的一段时间内，仍有大范围的增减。而这正是裂纹进行三次明显的曲裂运动的时刻。而试件A和试件B在裂纹扩展后期，加速度幅值较小，速度的减小过程相对较慢，裂纹的扩展相对稳定。因此，速度与加速度的变化反应了试件断裂过程中裂纹扩展的变化情况。

2.4动态应力强度因子分析

通过测量得到的焦散斑特征尺寸和式(1)、(2)计算得到三种试件的主、次裂纹应力强度因子数值随时间的变化规律(见图8)。

对于所有预制裂纹尖端上的应力强度因子，他们的变化规律基本相同，而处于复合应力场的裂纹尖端，KⅠ一直大于KⅡ。在裂纹起裂前的能量积累阶段，应力强度因子不断增长，一段时间后试件A、试件B和试件C的主裂纹KⅠ达到最大值，分别为1.81 MN/m3/2、2.13 MN/m3/2和2.38 MN/m3/2；而次裂纹的应力强度因子达到最大值的时间要迟于主裂纹，试件B和试件C的次裂纹KⅠ相应的最大值为1.52 MN/m3/2和1.68 MN/m3/2，随后应力强度因子开始逐渐减小，在落锤冲击试件到试件断裂的整个阶段，应力强度因子一直表现出振荡变化。落锤冲击产生的应力波在试件内传播时，首先会寻求应力更易集中的区域积聚，以达到释放能量的目的。在裂纹开裂前，应力波传播到试件边界成反射波，应力波和反射波与裂纹尖端的相互作用造成了应力强度因子的振荡变化，由于这种相互作用的无规则性，导致了应力强度因子振荡的不规律性。裂纹开裂后，能量快速释放，而剩余的能量转化为动能驱动裂纹扩展；同时，裂纹尖端处的应力波与反射波持续的相互叠加，能量进一步积累并推动着裂纹不断的向前扩展，直至裂纹贯通试件。

从图8(b)中还观察到，两种试件的次裂纹的应力强度因子在中期有一个快速下降的过程(试件B 392～431 μs ，试件C 601～640 μs)。这是由于主裂纹在扩展过程中，两条裂纹的尖端激发出的应力波与试件内部已经存在的波之间叠加，发生了更为复杂的波与裂纹的相互作用。同时，从裂纹扩展路径、速度与加速度的变化曲线中观察到，裂纹在这个阶段的曲裂运动很明显，裂纹扩展速度也达到最大。这可能是次裂纹尖端积聚的能量转移到主裂纹处释放，进一步促进了主裂纹处的曲裂，导致了次裂纹处的应力强度因子的减小。

图8　裂纹尖端应力强度因子随时间变化曲线 Fig.8 The change curves of crack tip stress intensity factor with time

对比动态应力强度因子、裂纹扩展速度和加速度的曲线可知，速度与加速度是随着应力强度因子的变化而变化的。因此，把应力强度因子作为衡量试件断裂的参数可以很好地反映裂纹起裂、扩展与贯通的全过程。

3结论

冲击荷载作用下，含双裂纹且主裂纹在冲击点正下方的试件起裂时间最早，裂纹扩展后期朝向次裂纹方向发生约4°的偏移；含Ⅰ型单裂纹的试件起裂时间次之，裂纹扩展路径呈直线；含双裂纹且两条裂纹均偏置于冲击点的试件起裂时间最晚，扩展过程中发生明显的曲裂现象。

三种试件的速度与加速度的变化曲线表明，裂纹的扩展是非匀速的。同时，裂纹扩展过程中曲裂现象越严重，扩展的最大速度就越小。

在落锤冲击试件到试件断裂的整个阶段，应力强度因子一直表现出振荡变化。含双裂纹的试件，在主裂纹扩展中期，次裂纹上的应力强度因子有一个快速下降的过程。

参 考 文 献

[1] 许蔚，姚学锋. 线性规律功能梯度材料断裂行为实验研究[J].力学学报,2008,40(4):485-495.

XU Wei, YAO Xue-feng. Experimental study on fracture behavior of linear functionally gradient materials[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008,40(4): 485-495.

[2] 贾敬辉，张永彬. 动荷载作用下三点弯曲梁的破坏形式与偏置裂纹位置的关系[J].武汉理工大学学报,2012,34(11):84-87.

JIA Jing-hui, ZHANG Yong-bin. Relations between the location of the notch and the failure mode in three point bending beam under the dynamic loads[J]. Journal of Wuhan University of Technology, 2012, 34(11):84-87.

[3] 朱万成，唐春安，扬天鸿，等. 偏三点弯曲岩石试件中裂纹扩展过程的数值模拟[J]. 东北大学学报, 2002, 23(6): 591-594.

ZHU Wan-cheng, TANG Chun-an, YANG Tian-hong, et al. Numerical simulation on the propagation of crack in theeccentric three-point bending specimen[J]. Journal of Northeastern University, 2002, 23(6): 591-594.

[4] 黄明利，朱万成，逄铭彰. 动载荷作用下含偏置裂纹三点弯曲梁破坏过程的数值模拟[J].岩石力学与工程学报, 2007,(26):3384-3389.

HUANG Ming-li, ZHU Wan-cheng, PANG Ming-zhang. Numerical simulation of dynamic failure processes of three point bending beam with offset notch[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,(26):3384-3389.

[5] 岳中文，杨仁树，郭东明，等. 爆炸应力波作用下缺陷介质裂纹扩展的动态分析[J]. 岩土力学, 2009, 30(4):949-954.

YUE Zhong-wen,YANG Ren-shu, GUO Dong-ming, et al.Dynamic analysis of crack propagation in media containing flaws under the explosive stress wave[J]. Rock and Soil Mechanics, 2009, 30(4):949-954.

[6] 肖同社，杨仁树，边亚东，等. 含节理岩体爆生裂纹扩展的动焦散模型实验研究[J]. 实验力学, 2006, 21(4):539-545.

XIAO Tong-she, YANG Ren-shu, BIAN Ya-dong, et al. Dynamic caustics model experiment of blasting crack propagating on joint rock[J]. Journal of Experimental Mechanics, 2006, 21(4):539-545.

[7] 励争，樊金武，王君，等. 用焦散线法研究PP/PA6/POE-g-MA的动态断裂性能[J].实验力学,2006,21(3):357-362.

LI Zheng,FAN Jin-wu, WANG Jun, et al. Dynamic fracture properties of PP/PA6/POE-g-MA studied by caustics method[J]. Journal of Experimental Mechanics, 2006,21(3): 357-362.

[8] 杨仁树，岳中文，肖同社，等. 节理介质断裂控制爆破裂纹扩展的动焦散试验研究[J].岩石力学与工程学报, 2008, 27 (2):244-250.

YANG Ren-shu, YUE Zhong-wen, XIAO Tong-she, et al. Dynamic caustics experimental on crack propagation of jointed medium fracture with controlled blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (2):244-250.

[9] 边亚东，胡江春，潘洪科. 含裂纹模拟岩石材料动焦散实验研究[J].安徽建筑，2013,(3):208-209.

BIAN Ya-dong, HU Jiang-chun, Pan Hong-ke. Dynamic caustic experimental research on simulating rock material with preset crack[J].Anhui Architecture,2013,(3):208-209.

[10] 刘宁, 姚学锋，金观昌. 碳纤维布补强梁裂尖奇异性的光学焦散线实验研究[J].光学技术,2003,29(5):530-533.

LIU Ning, YAO Xue-feng, JIN Chang-guan.Optical caustic experimental study on crack tip singularity of carbon fiber cloth strengthened beams[J]. Optical Technique, 2003,29(5): 530-533.

[11] 姚学锋，方竞. 冲击载荷下扩展裂纹尖端动态能量释放率分布的焦散线分析[J].爆炸与冲击，1996,16(2): 111-116.

YAO Xue-feng, FANG Jing. Analysis of caustics on dynamic energy release rate of running crack tip under impact load[J]. Explosion and Shock Waves. 1996,16(2): 111-116.

[12] Kalthoff J F, Winkler S, Beinert J. Dynamic stress-intensity factors for arresting cracks in DCB specimens[J]. International Journal of Fracture, 1976,(12):317-319.