子系统参数对双层隔振系统固有特性的影响

第一作者 陈俊 男，博士生，1989年4月生

通信作者 董大伟 男，教授，博导，1963年4月生

子系统参数对双层隔振系统固有特性的影响

陈俊，闫兵，董大伟，鲁志文，王媛文

(西南交通大学 机械工程学院,成都610031)

摘要：为了研究子系统参数对双层隔振主系统固有特性的影响规律，将系统抽象为3自由度动力学模型，推导了系统动力放大系数(振幅比)和无量纲固有频率(固有频率比)解析式以及振型和解耦度与子系统质量比和刚度比的关系式，进而研究了子系统质量比和固有频率比对双层隔振主系统固有特性(固有频率、解耦度)的影响规律。在此基础上，针对含多个子系统的内燃动车动力包双层隔振系统，仿真计算了空冷子系统的质量和刚度对双层隔振12自由度主系统固有特性的影响规律。研究结果对双层隔振系统子系统的设计具有指导意义。

关键词：子系统；双层隔振系统；固有特性；动力包

基金项目：牵引动力国家重点实验室

收稿日期：2013-11-08修改稿收到日期：2014-03-07

中图分类号:TH212；TH213.3文献标志码： A

Effects of subsystem parameters on natural characteristics of a double-layer vibration isolation system

CHENJun,YANBing,DONGDa-wei,LUZhi-wen,WANGYuan-wen(School of Mechanical Engineering, Southwest Jiaotong University,Chengdu 610031, China)

Abstract:In order to study the effects of subsystem parameters on natural characteristics of a double-layer vibration isolation system(DLVIS), a 3-DOF dynamic model was established, and the analytical expressions of dynamic magnification factor and dimensionless natural frequencies of the system were deduced, then, the relation expressions involving the decoupling level and vibration modal shapes of the isolation system to the mass ratio and stiffness ratio of subsystems were derived. Afterwards, the effects of the mass ratio and stiffness ratio of subsystems on the DLVIS main system natural characteristics were studied. Furthermore, the effects of an air cooling subsystem’s mass and stiffness on the natural characteristics of a 12-DOF main system were simulated for a DMU power pack DLVIS with multiple subsystems. The results provided a reference for design of subsystems of a double-layer vibration isolation system.

Key words: subsystem; double-layer vibration isolation system; natural characteristics; power pack

双层隔振系统因为其良好的高频隔振特性，广泛应用于交通运输和船舶等诸多领域[1]。双层隔振系统的常用形式有浮笩和动力包两种，两者都有一个共同的特征即隔振系统的中间构架上还存在一个或多个子系统。回顾双层隔振理论和技术的发展，许多学者从不同角度对双层隔振系统的特性进行了研究[2-9],但主要集中在主系统各参数对双层隔振系统隔振特性影响的研究，鲜有考虑子系统对双层隔振系统隔振特性的影响。Gina Lee-Glauser等研究了运载火箭及其子系统的隔振特性，但仅局限在对子系统被动隔振的研究，并没有深入探讨子系统与主系统的耦合振动特性。文献[11]仅给出了当质量比小于0.1时子系统对隔振系统几乎不产生影响的结论，并没有更深入地探讨子系统对隔振系统固有特性的影响规律。而在工程实践中，由于受到空间布局和安装等因素限制，子系统往往安装在远离隔振系统质心的位置，此时子系统相对隔振系统质心的转动惯量比可能远远大于0.1，这种情况下子系统对主系统固有特性的影响不能被忽略，因此很有必要对其进行深入探究。

针对上述问题，将带有子系统的双层隔振系统抽象为三自由度动力学模型，建立动力学方程并推导出系统动力放大因子和无量纲固有频率公式。继而深入探讨子系统对双层隔振系统固有特性的影响，其结论普遍适用于带子系统的双层隔振系统。在此基础上，针对国内首次采用的动力包双层隔振系统，深入研究空冷子系统物理参数对双层隔振12自由度主系统固有特性的影响规律，旨在为动力包子系统的设计提供参考和指导。

1三自由度模型固有特性影响规律研究

子系统的引入对双层隔振主系统的固有频率、振型、能量解耦度都会产生影响。如果子系统的参数设计不合理，将会严重减弱双层隔振系统的隔振性能，相反,一个设计合理的子系统能有效地改善双层隔振系统的隔振性能。通过深入探讨子系统对双层隔振系统固有特性的影响，为进行隔振设计时子系统参数的选取提供理论依据。

1.1含子系统的双层隔振系统动力学模型

带子系统的双层隔振系统模型可抽象为如图1所示三自由度动力学模型，其中m1、m3分别为双层隔振主系统的一级、二级质量，k1、k3分别为双层隔振主系统的一级、二级刚度，m2、k2分别为子系统的质量和刚度。

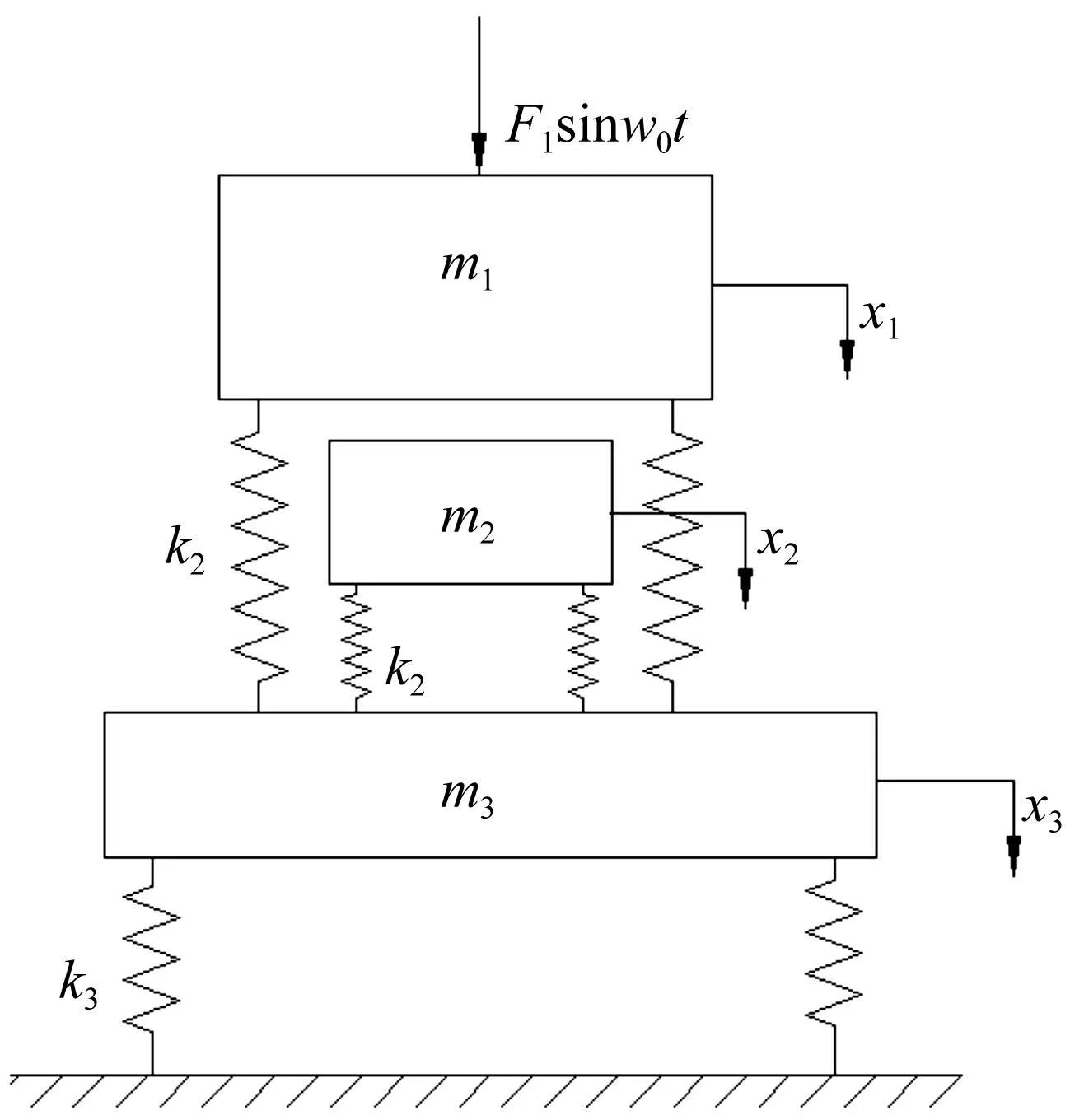
图1　带子系统的双层隔振系统示意图 Fig.1 Schematic diagram of double-layer vibration isolation system including subsystem

根据动力学抽象模型可列出含子系统的双层隔振系统动力学微分方程：

(1)

1.2子系统质量比对双层隔振系统振幅比的影响

只考虑系统强迫振动的稳态响应，式(1)的解可表示为x={A}eiωt，引入符号：

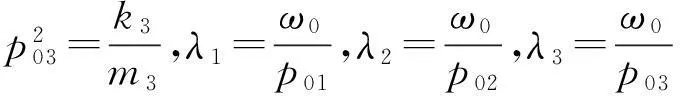
将一级、二级振幅A1、A2改写为无量纲的形式：

(2)

式中：

由式(2)可知双层隔振系统一级、二级主系统的振幅比都为子系统质量比μ2的函数。根据隔振系统的设计原则[11](以下各参数都根据此原则选取)，取λ1=1.3，λ2=1.2，λ3=0.8，μ1=0.5，计算一级、二级主系统振幅比与子系统质量比μ2的关系曲线(见图2)。

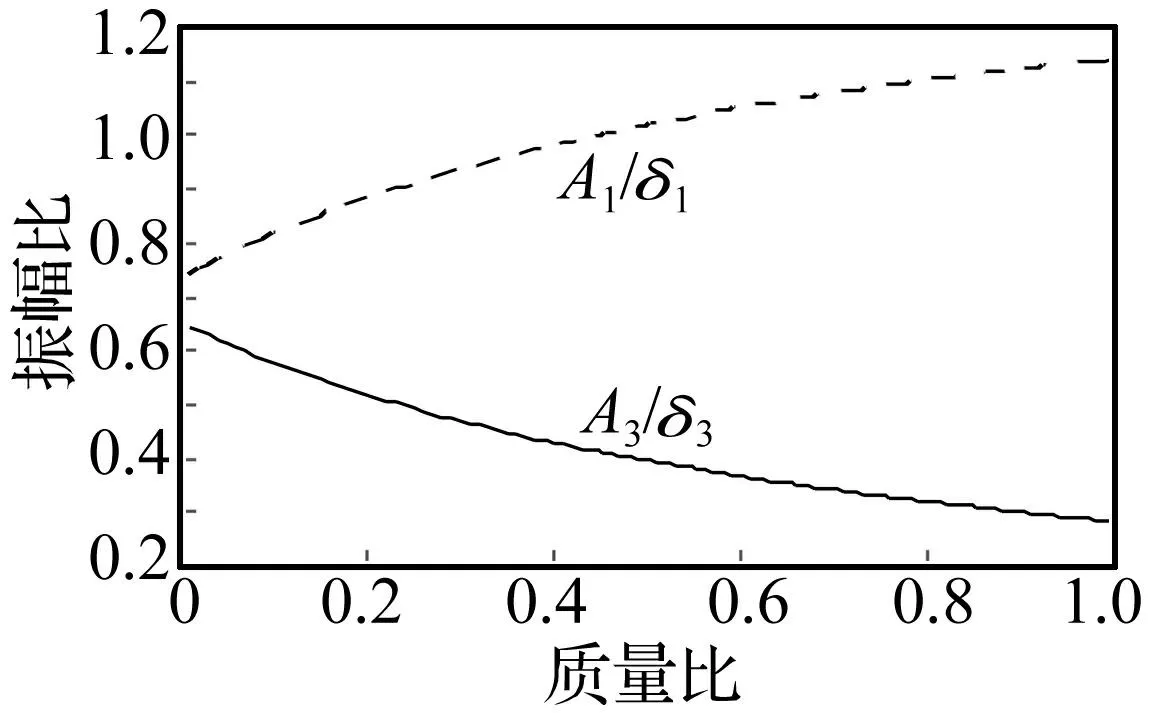
图2　质量比μ 2与振幅比A 1/ 1，A 3/ 3的关系 Fig.2 The relationship between mass ratio μ 2and vibration amplitude A 1/ 1，A 3/ 3

从图2可知随着质量比μ2的增大， 振幅比A1/1增大，A3/3减小。说明子系统质量的增加会使一级主系统振动更为激烈，但相应又会减弱二级主系统的振动，这有利于激振力的隔离，但同时又会增大振动烈度恶化动力设备的工作环境。在设计子系统时要充分权衡二者的重要性，选择合适质量的子系统。当子系统的质量比>0.2时子系统对一级、二级主系统的振幅比的影响>20%，随着质量比μ2的增大子系统对主系统振幅比的影响变小。

1.3子系统质量比对双层隔振系统固有特性的影响

上文中三自由度系统动力学模型的自由振动的特征方程为：

(4)

展开整理后，有：

aω6+bω4+cω2+d=0

(5)

式中：

a=m1m2m3

b=-((k1+k2+k3)m1m2+k1m2m3+k2m1m3)

c=(k2+k3)k1m2+(k1+k3)k2m1+k1k2m3

d=-k1k2k3

引入符号：

将式(5)的解改写为无量纲的形式可得：

式中：

a′=μ1μ2

b′=μ2+μ2ν2+μ2ν1+μ1μ2+μ1ν2

c′=μ2ν2+μ2ν1+μ1ν2+ν1ν2+ν2

d′=ν1ν2

由式(4)可知系统的自由振动方程可化为：

(7)

式中:Δω为无量纲固有频率(下文都用固有频率比代替)，Δω=ωr/ω。

将式(6)代入式(7)可求得对应于无量纲固有频率的特征向量即系统的阵型{ΔAr}。因为式(7)与式(4)完全等价所以有

ΔAr=Ar

(8)

当系统以第j阶模态振动时，定义系统的振动能量分布矩阵为：

(9)

式(9)中：φ(k,j),φ(l,j)分别为第j阶振型的第k和第l个元素；M(k,j)为系统质量矩阵的第k行，第l列元素；ωj是第j阶固有频率，k,l,j=1,2,3。

当系统以第j阶模态振动时，第k个广义坐标分配的能量占系统总能量的百分比为：

(10)

将式(10)等效变化为：

(11)

式(11)中:U为系统的质量比矩阵：

通过观察发现，式(11)恰好为对应于式(7)所代表的振动系统的能量解耦度表达式。

根据以上分析可以得出结论：系统固有频率、振型和能量解耦度只与系统各物理参数之间的相对关系有关，与大小无关。

EPjk的大小反映系统解耦度的高低，若EPjk=100%，则系统以第j阶模态振动时能量全部集中在第k个广义坐标上。此时振型矩阵[Δφ]中第j列和第k行的非对角元素全为零，即系统的第j阶模态振动完全解耦。

图3　质量比μ 2对主系统固有特性的影响 Fig.3 Effect of mass ratio μ 2on the natural characteristics of main vibration isolation system

为研究子系统质量比μ2对双层隔振主系统固有特性的影响，图3给出了当μ1=0.5，ν1=2，ν2分别等于0.6μ2和1.6μ2时，一级、二级主系统的固有频率比和能量解耦度与质量比μ2的关系曲线。从图3可知，质量比μ2对一级主系统的固有频率比几乎无影响，而对二级子系统的固有频率比的影响较明显；前者随质量比μ2的增大而减小，后者随质量比μ2的增大而增大。子系统固有频率大于ω时对二级主系统的频率比的影响较明显，此时主系统解耦度随质量比μ2的增大而减小。相反子系统的固有频率小于ω时主系统的解耦度随μ2的增大而增大。质量比μ2对一级主系统解耦度的影响非常明显，而对二级主系统的解耦度基本无影响。

1.4子系统固有频率比对双层隔振系统固有特性的影响

子系统质量和刚度的改变都会引起本身固有频率的改变，图4为分别取μ1=0.5，ν1=2，ν2=0.3和μ1=0.5，ν1=2，μ2=0.5得到主系统的固有频率比和解耦度分别与μ2、ν2的关系。

图4　子系统固有频率比与主系统固有特性的关系 Fig.4 The relation between subsystems’ natural frequency and natural characteristics of main vibration isolation system

从图4可知，一级主系统的固有频率比随质量比μ2的增加而减小，随刚度比ν2的增大而增大；且当刚度比ν2大于0.5时一级主系统固有频率基本不随刚度比ν2变化。二级主系统固有频率比随刚度比ν2的增大而增大，随子系统的质量比μ2的增大而减小；且当质量比>0.3时二级主系统的固有频率基本不随质量比μ2变化。一级主系统固有频率比对质量比μ2的灵敏度高于刚度比ν2，二级主系统固有频率比对刚度比ν2的灵敏度高于质量比μ2。一级主系统的解耦度随质量比μ2和刚度ν2的增大先减小再增大，在子系统和主系统固有频率比相近时(0.4附近)出现拐点。二级主系统的解耦度随质量比μ2的增大而增大，随刚度比的增大而减小。一级主系统解耦度对质量比μ2和刚度比ν2的灵敏度均高于二级主系统。

2动力包双层隔振主系统固有特性影响规律研究

前面所采用的双层隔振系统三自由度动力学模型，没有考虑子系统的安装位置，并假设一级、二级主系统和子系统的质心位置是重合的。所得结论是上述假设条件下的基本规律。而实际中双层隔振系统一级、二级主系统和子系统三者间的质心位置不重合，子系统与主系统质心间的距离往往较大。这使得子系统与主系统各自由度之间的耦合关系更为复杂，子系统各参数对主系统固有特性的影响规律也变得更为复杂。为此，针对国内首次采用的内燃动车动力包双层隔振多子系统，系统地研究子系统各参数对主系统固有特性的影响，以便更好的为同类型的双层隔振系统子系统的设计提供参考。

2.1隔振系统介绍

动力包双层隔振系统见图5，其中柴油机和发电机通过连接套刚性连接构成双层隔振系统的一级主系统，通过五个一级隔振器安装于构架上。构架和刚性安装于其上的水箱、空滤、消音器等构成双层隔振系统的二级主系统，通过四个二级隔振器安装于基础上。空冷装置和静压泵组分别通过四个隔振器安装于构架上构成双层隔振系统的两个子系统。

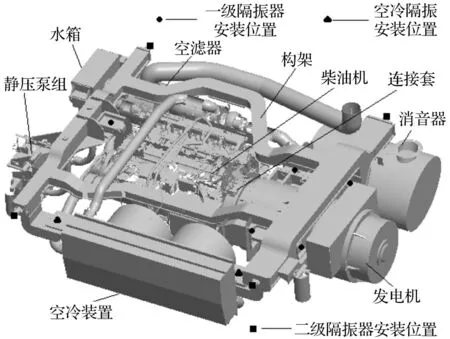
图5　动力包双层隔振系统实物图 Fig.5 Physical diagram of powerpack double-layer isolation system

2.2隔振系统动力学模型

以柴油发电机组的质心为原点建立含多个子系统的双层隔振系统的离散参数模型，其子系统的参数见表1。从表1可知静压泵组子系统的质量比和惯量比都<0.2，因此可以忽略其对双层隔振主系统的固有特性的影响，单独分析空空冷却子系统对双层隔振主系统固有特性的影响。根据以上分析，可将该内燃动车双层隔振多子系统简化为如图6所示的18自由度动力学模型。

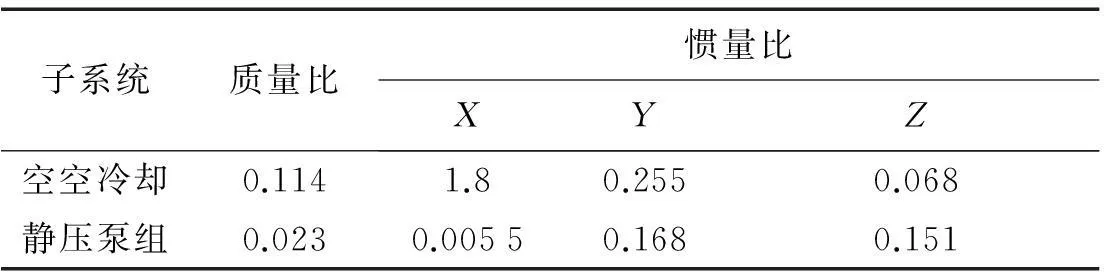
表1　双层隔振子系统系统参数

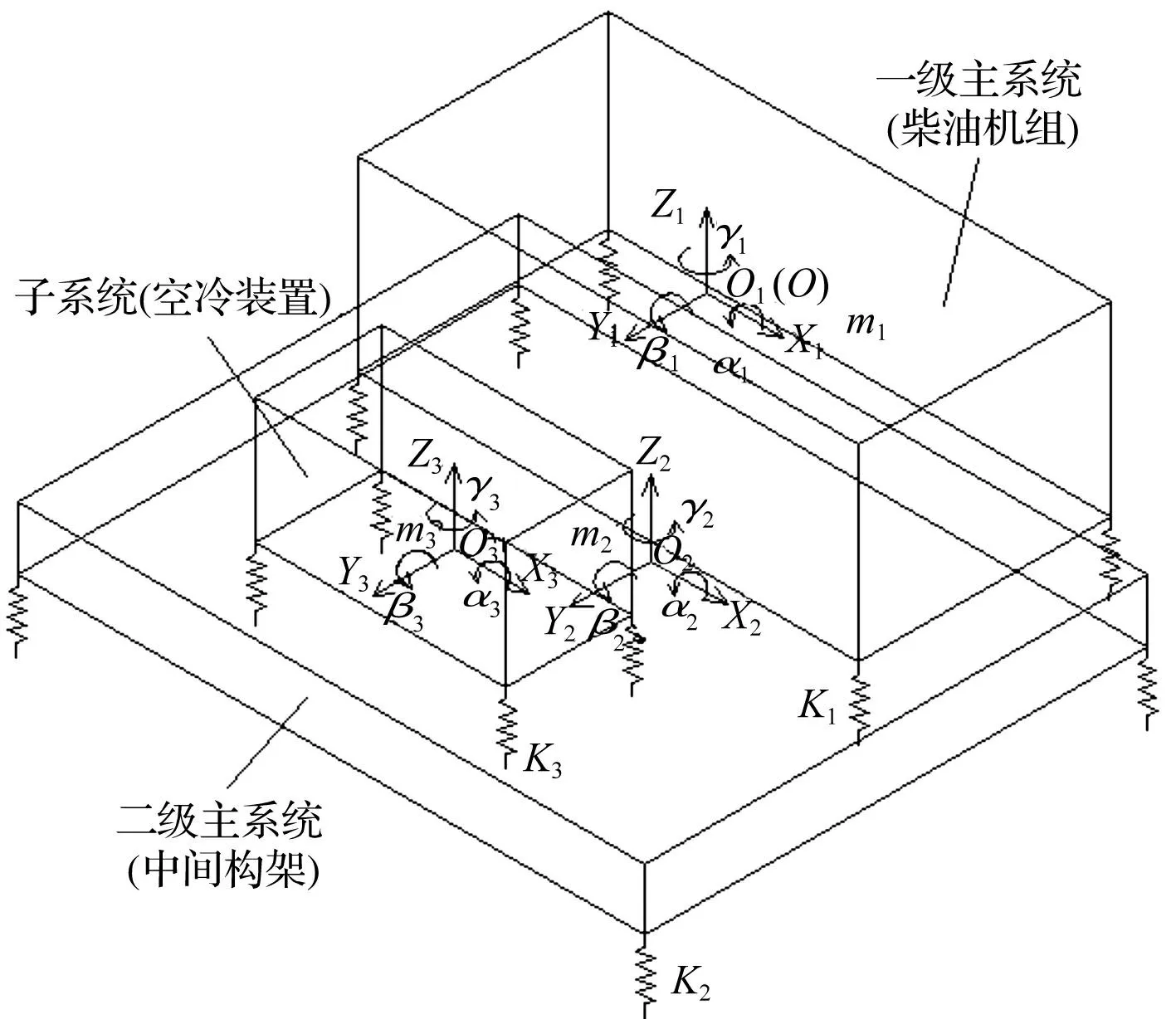
图6　内燃动车动力包双层隔振系统动力学模型 Fig.6 Dynamic model of diesel railcar powerpack double-layer isolation system

图6中O,O1,O2,O3分别为参考坐标原点和机组、空空冷却器、中间构架的质心。O-XYZ和(α,β,γ)为参考坐标系以及其惯性主轴。O1-X1Y1Z1,O2-X2Y2Z2,O3-X3Y3Z3和，(α1,β1,γ1),(α2,β2,γ2),(α3,β3,γ3)别为机组、中间构架和空空冷却的动坐标系和惯性主轴。系统的动力学方程为：

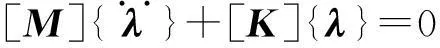
(12)

式中：

[K]=

[Mii]和[Kii]分别为子系统的质量矩阵和刚度矩阵。

设该方程组的解为x={A}eiωt，引动力矩阵 [D]=[K]-1[M]，方程可化解为：

(13)

这是关于动力矩阵[D]的标准特征值问题。此特征值问题的解，特征值ωr和相应的广义特征向量{Ar}，便是系统各固有频率的平方和对应振型。

2.3空空冷却子系统质量对动力包双层隔振主系统固有特性的影响

为研究空冷子系统质量对机组和构架组成的双层隔振主系统的影响，参考市场上同类型空冷装置的质量波动范围，取空空冷却系统的质量m3的变化范围为200～400 kg，得到动力包双层隔振主系统的固有特性随空冷装置质量m3的关系(见图7)。

图7　空空冷却器质量对主系统固有特性的影响，X 1，Y 1，Z 1，X 2，Y 2，Z 2， X 3，Y 3，Z 3，α 1， β 1，γ 1，α 2，β 2，γ 2，α 3，β 3，γ 3为各主坐标方向的固有频率或能量解耦度，下同 Fig.7 Effect of air to air cooling subsystem’s mass m 3 on the natural characteristics of main vibration isolation system

从图7可知主系统的12个固有频率随子系统质量的增大而减小，α1方向的固有频率对m3的灵敏度最高，其它主自由度方向固有频率的变化很小。因为在该方向子系统的质心离第一级主系统的质心距离最大，即m3的变化会引起较大的惯量比的变化，而其他主自由度方向惯量比的变化很小，这与前面所述三自由度系统的规律是一致的。一级子系统解耦度对m3的灵敏度高于二级子系统，x2，α1，α2，γ2向解耦度随m3的增大而增大，其它方向的解耦度随m3的增大而减小。对照图4可知x2，α1，α2，γ2方向的惯量比要大于拐点的惯量比，而其它自由度方向的惯量比要小于拐点的惯量比。α1，β1，γ1向的解耦度对m3的灵敏度较大，其他主方向的解耦度随m3的变化不大，这同样可以用对固有频率的影响来解释。对于动力包双层隔振系统，其主要激振力为α向倾倒力矩。为了避免隔振系统在激振力方向产生严重的耦合振动一般要求α1，α2向解耦度尽量大，即要求子系统的质量要尽量大。而实际工程设计中往往希望子系统质量尽量小，这两者是相互矛盾的。此外子系统质量的增大会引起β1，γ1向的解耦度迅速变小，但因为这些方向与激振力方向并不耦合，所以设计子系统时可以在适当减小子系统质量和牺牲其它方向解耦度的情况下优先考虑α1，α2向解耦度。

图7中γ1向解耦度在质量m3为290 kg时发生较明显的突变，同时γ1向固有频率也发突变。通过图8、图9、图10可知，随着m3的增大，γ1向固有频率和Z3向固有频率变小且越来越接近。当m3为290 kg时两主模态方向固有频率相等，解耦度迅速变小，振型的阶数发生互换，系统发生较强烈的耦合振动。随着m3的继续增大，两固有频率的差距变大，两主坐标方向的耦合程度随之变小。

图8 空空冷却器质量m3与γ1和Z3向振型阶数的关系Fig.8Therelationshipbetweenairtoaircoolingsubsystem’smassm3andvibrationmodeorderofγ1andZ3图9 空空冷却器质量m3和γ1和Z3向固有频率的关系Fig.9Therelationshipbetweenairtoaircoolingsubsystem’smassm3andnaturalfrequencyofγ1andZ3图10 空空冷却器质量m3和γ1和Z3向解耦度的关系Fig.10Therelationshipbetweenairtoaircoolingsubsystem’smassm3anddecouplingdegreeofγ1andZ3

2.4空空冷却子系统刚度对动力包双层隔振主系统固有特性的影响

从三自由度模型可以看出子系统的刚度同样对主系统的固有特性有很大的影响，为了具体研究空空冷却子系统的刚度对由机组和构架组成的12自由度主系统固有特性的影响，取子系统垂向刚度K3变化范围从100～500 kN/m变化，得到主系统固有特性和空空冷却子系统刚度的关系(见图11)。

图11　空空冷却器刚度对主系统固有特性的影响 Fig.11 Effect of air to air cooling subsystem’s mass K 3 on the natural characteristics of main vibration isolation system

从图11可知主系统固有频率总的趋势为随子系统刚度K3的增大而增大。二级主系统固有频率对子系统刚度K3的灵敏度高于一级主系统。α1，α2方向的固有频率对K3的灵敏度最高且变化均匀，其它方向的固有频率除突变段外基本不随K3变化，这与三自由度系统的规律是一致的。主系统各主方向的解耦度不再随K3单独变化，存在多处突变，但总体上随K3的增大而减小。在突变位置解耦度一般都<50%，说明该主坐标方向的振动能量有很大一部分转移到子系统上，即两者间存在严重的能量耦合，此时固有频率往往会产生突变，并且振型阶数也会发生改变。另外，动力包双层隔振系统在运行一段时间后，隔振器性能会发生变化，隔振器刚度会与初始值有一定的偏差，所以在选择子系统隔振器刚度时除了要考虑激振力方向解耦度最优外，还要注意不要使隔振刚度落在突变段附近，避免因为隔振器刚度的小幅度变化而使隔振系统的隔振性能急剧变差。

双层隔振系统为了兼顾α1，α2方向的解耦度和解耦的稳定性，空空冷却子系统隔振器刚度范围应选择在图11中两矩形框的交集内。图12为隔振器刚度为290 kN/m时，根据国标(TB/T3164-2007)进行实验测得的双层隔振系统振动烈度随转速的变化曲线。从图中可以看出在600 r/min转速工况的振动烈度等级为A(良好工作状态)，其余各转速工况的振动烈度等级均为B(正常工作状态)，该子系统的设计满足设计要求。

图12　双层隔振系统振动烈度测试结果 Fig.12 Vibration intensity test results of double-layer isolation system

3结论

(1) 系统固有频率、振型和能量解耦度只与系统各物理参数之间的相对关系有关，与大小无关。

(2) 子系统质量的增加有利于系统激振力的隔离，但会恶化动力设备的振动情况。在设计子系统时要充分权衡二者的重要性，选择合适质量的子系统。子系统固有频率比一级主系统大时，增加子系统的质量有利于提高主系统的解耦度，相反子系统固有频率比一级主系统固有频率小时，减小子系统的质量有利于提高主系统的解耦度。因此，在进行隔振设计时，当子系统质量较大时，应选择刚度比较大的隔振器；当子系统质量较小时应选择刚度比较小的隔振器。

(3) 双层隔振主系统的12个固有频率随子系统质量的增大而减小，质心坐标离主系统质心坐标距离大则主方向固有频率对子系统质量的灵敏度高。选择子系统隔振器刚度时除了要考虑使激振力方向解耦度最优外，还要注意隔振刚度不可落在解耦突变区域附近，避免因为隔振器刚度的小幅度变化而使隔振系统的隔振性能变差。

参 考 文 献

[1] 潘延亮. 发动机隔振系统优化设计研究[D]. 成都：西南交通大学, 2012.

[2] 张志，张兆会，董森，等.橡胶双层减振与隔振系统冲击响应研究[J].振动与冲击,2013,32(23):126-129.

ZHANG Zhi, ZHANG Zhao-hui, DONG Sen, et al. Shock response of a rubber double-deck vibration isolation system[J].Journal of Vibration and Shock, 2013, 32(23): 126-129.

[3] 肖斌,李彪，夏春艳，等, 基于功率流法双层隔振系统振动传递 [J]. 机械工程学报, 2011,47(5): 106-113.

XIAO Bing,LI Biao, XIA Chun-yan,et al.Power flow method used to vibration transmission for two-stage vibration isolation system [J]. Journal of Mechanical Engineering, 2011,47(5):106-113.

[4] 苏荣华, 彭晨宇与丁文文, 设计参数对双层隔振系统动态性能影响的研究[J]. 应用基础与工程科学学报, 2008,16(6): 863-869.

SU Rong-Hua, PENG Chen-yu, DING Wen-wen, Research on effect of design parameter on dynamic properties of two-stage vibration isolation system [J]. Journal of Basic Science and Engineering,2008,16(6):863-869.

[5] 张蔚波, 牛军川,宋济平. 功率流分析中的柔性振源子系统 [J]. 机械工程学报, 2007(1): 129-132.

ZHANG Wei-bo, NIU Jun-chuan, SONG Ji-ping. Flexible vibration source subsystem in power flow analysis [J]. Journal of Mechanical Engineering, 2007(1): 129-132.

[6] 袁惠群. 具有分布质量的双层隔振系统隔振特性分析 [J]. 振动与冲击, 1996,15(3):61-64.

YUAN Hui-qun. Study on the properties of two-stage vibration isolation system with distributed mass [J].Journal of Vibration and Shock, 1996,15(3): 61-64.

[7] 张华良, 瞿祖清,傅志方. 浮筏隔振系统各主要参数对系统隔振性能的影响 [J]. 振动与冲击, 2000,19(2):7-10.

ZHANG Hua-liang, QU Zu-qing, FU Zhi-fang, Effect of main parameter on vibration isolation properties of floating raft [J]. Journal of Vibration and Shock, 2002,19(2): 7-10.

[8] Hu F, Yang J, Zhong Q. An experimental and theoretical study on two-layer vibration isolation of a diesel generating set in an oil tanker[J]. Maritime Industry, Ocean Engineering And Coastal Resources, 2008(1-2): 373-378.

[9] Chen X, Qi H, Zhang Y, et al. Optimal design of a two-stage mounting isolation system by the maximum entropy approach[J]. Journal Of Sound And Vibration. 2001, 243(4): 591-599.

[10] Lee-Glauser G,Ahmadi G.Vibration isolation oflaunch vehicle payload and its subsystem [J]. Journal of Aerospace Engineering,1995,8(1):1-8.

[11] 谭达明. 内燃机振动控制[M]. 成都: 西南交通大学出版社, 1993.