一种非分层海洋中的声线计算方法

第一作者 唐俊峰 男，博士,讲师 1979年生

一种非分层海洋中的声线计算方法

唐俊峰，杨士莪，朴胜春

(哈尔滨工程大学 水声技术国防科技重点实验室，哈尔滨150001)

摘要：在浅海环境中，声速剖面和海底深度在水平方向上的变化都会对声传播产生较大的影响。将声速剖面用前几阶经验正交函数来表示，在一定范围的海域各阶经验正交函数系数可以近似为随水平距离线性变化，提出了一种非分层海洋中的声线计算方法，可以计算到达接收水听器的本征声线和传播时间。该方法计算速度快，计算精度较高，可以用于海洋中的声速剖面快速反演。

关键词：非分层；本征声线；传播时间；经验正交函数

基金项目：哈尔滨工程大学基础研究基金(HEUFT07024)

收稿日期：2013-12-11修改稿收到日期：2014-02-20

中图分类号:TB566文献标志码： A

A method for calculating acoustic ray in unstratified ocean

TANGJun-feng,YANGShi-e,PIAOSheng-chun(State Laboratory of Underwater Acoustic Technology,Harbin Engineering University,Harbin 150001,China)

Abstract:The horizontal variations of sound speed profile and ocean water depth have a significant effect on acoustic propagation in shallow sea water. Here, a method for calculating sound travel time based on the ray theory in unstratified ocean was proposed. An efficient algorithm was applied to seek eigen acoustic rays arriving at hydrophones. The sound speed profile could be described approximately using empirical orthogonal functions (EOFs) with a proper precision. The coefficients of EOFs vary linearly with horizontal distance in a certain sea area. It was shown that the proposed method can be used to calculate the travel time of eigen-acoustic rays arriving at hydrophones rapidly with a higher precision, it can be used for fast inversion of sound speed profile in ocean.

Key words: unstratified; eigen acoustic ray; travel time; empirical orthogonal function

在浅海环境下需要考虑海洋环境随距离变化的情况，射线声学方法适用于环境随距离变化的三维声场建模，并且射线声学理论下描述声场物理图像清晰，运算量小，实际应用广泛[1-3]。常用的三维声线模型Harpo将声线方程表示成一阶微分方程组的形式，采用龙格-库塔算法进行求解[4-5]，需要得到声速的导数信息，计算量较大。姜薇等[6-8]在超声层析成像中采用正三棱锥前向伸展算法进行三维声线跟踪。提出了一种非分层海洋中的三维声线计算方法，可以计算声线在声速剖面和海底深度随水平距离变化时的轨迹和传播时间，求取到达接收水听器的本征声线。该方法将声速剖面用经验正交函数来表示，由于声速剖面随水平距离变化时，声速在水平方向上的变化通常远小于在深度方向上的变化，在一定范围的海域内，经验正交函数的系数可以近似为在水平方向上随距离线性变化，可以近似得到声线轨迹的计算方法，快速计算声线的轨迹和传播时间。海底深度随水平距离变化时可以用逐步迭代逼近的方法快速计算声线在海底反射点的位置。该方法可以快速计算非分层海洋环境中声线的轨迹和传播时间，计算精度较高。

1声线轨迹和传播时间计算

1.1分层海洋中的声线计算

由射线声学理论[9]：

(1)

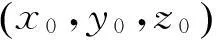
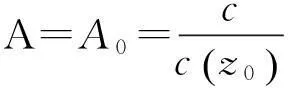
(2)

(3)

则：

(4)

(5)

(6)

传播时间为：

(7)

由式(4)～式(7)进行数值计算就可以求得声线的轨迹和传播时间。

1.2非分层海洋中的声线计算

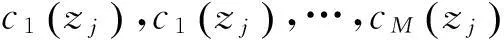
其中：

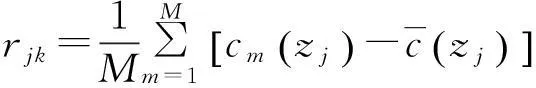
j,k=1,2,…,N

(8)

(9)

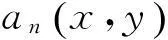
(10)

式中：

(11)

由于声速在水平方向上的变化远小于深度方向上的变化，由式(1)，式(10)可以近似得到：

(12)

(13)

式(12)，(13)数值计算时可以取一阶近似，第i+1步计算可表示为：

(14)

(15)

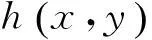
给定了声源的位置、声速剖面和海底深度等环境参数，声线传播的轨迹和传播时间就可以由式(4)～式(7)，式(12)，式(13)按一定的步长进行数值计算求得。

2本征声线求取

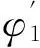
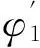
(3) 减小初始掠射角的变化范围和步长，重复“(1)”～“(3)”的步骤，直到计算精度满足设定的要求。

这时求取本征声线只需要在垂直扇面内进行搜索，运算量将大为降低。如果在同一位置不同的深度布放了多个接收水听器，到达各个接收水听器的本征声线可以同时计算。

3声线数值计算

利用以上的声线计算方法进行仿真计算。在三维坐标系下，声源的位置为(0 m,0 m,100 m)，接收水听器的位置为(50 km,0 m,50 m)。声速剖面用经验正交函数来表示，采用在南海某海域实测的声速剖面数据，图1是计算得到的平均声速剖面，图2是计算得到的前三阶经验正交函数。

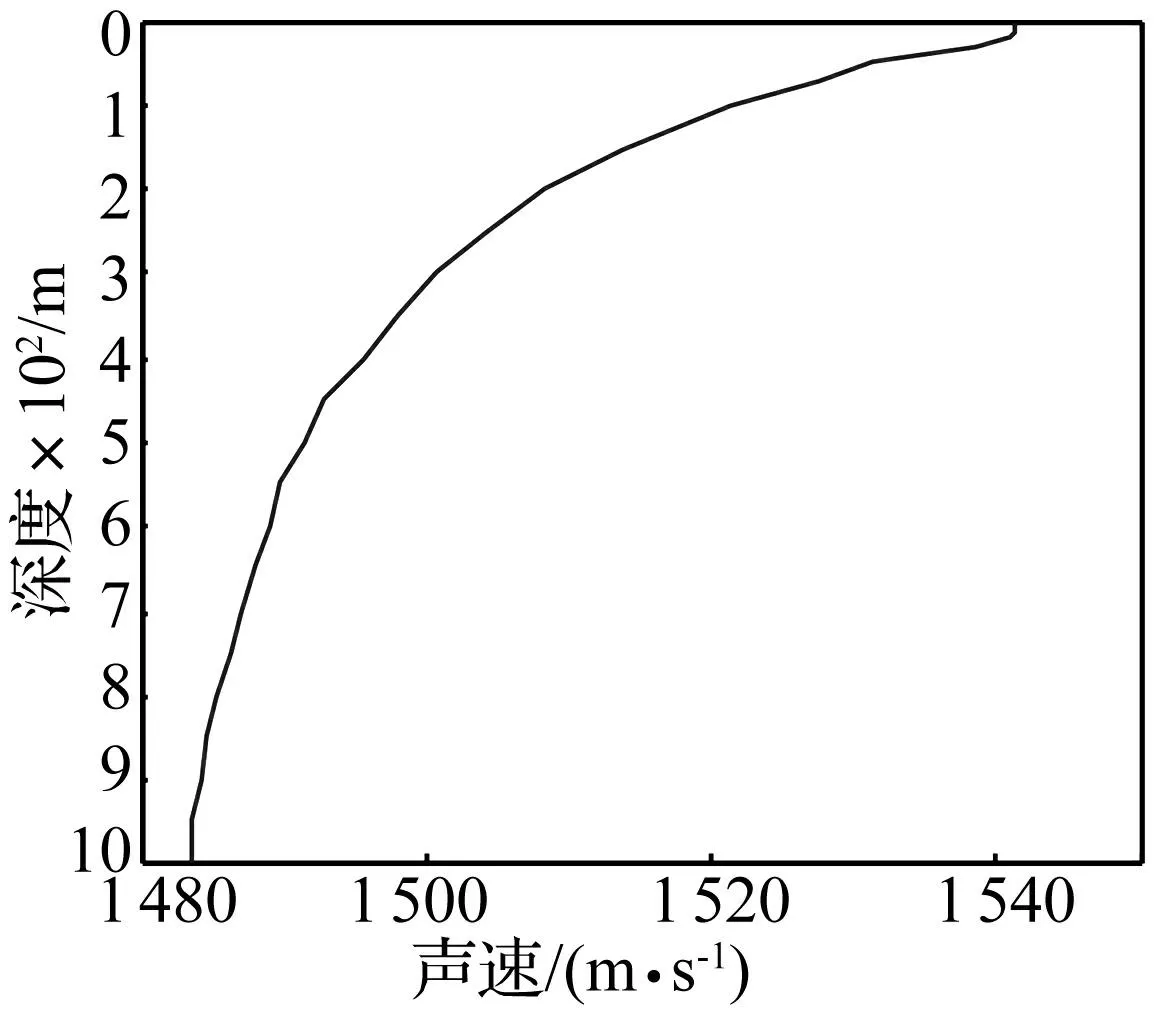
图1　平均声速剖面 Fig.1 The average of sound speed profiles

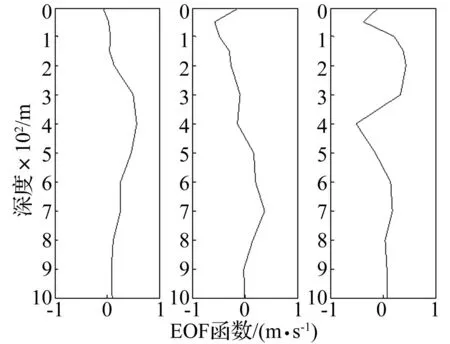
图2　经验正交函数 Fig.2 Empirical orthogonal functions

在声速剖面随水平距离变化的情况下，经验正交函数的系数在水平方向随距离发生变化，声速在水平方向上的变化通常较小，在式(10)中采用上述平均声速剖面和经验正交函数的数据，取a01=10；a11=0.06；a21=0.04；a02=-4；a12=0.03；a22=0.02；a03=3；a13=0.03；a23=0.02。海底为平坦的，深度为1 000 m。掠射角的搜索范围为-12°～12°，计算得到的本征声线的轨迹在垂直平面和水平面上的投影分别如图3、图4所示。

图3 本征声线在垂直平面内的投影Fig.3Theprojectionintheverticaldirectionofeigenrays图4 本征声线在水平面内的投影Fig.4Theprojectioninthehorizontaldirectionofeigenrays图5 本征声线的传播轨迹Fig.5Thetrajectoryofeigenrays

计算得到了8根本征声线，由于声速剖面随水平距离变化，声线在水平方向发生了偏转，在声源出射时指向海面方向的4根本征声线的初始掠射角、方位角和传播时间见表1。由于声线在水平方向发生了偏转，到达接收水听器的本征声线的初始方位角不为0。取a11,a21,a12,a22,a13,a23均为0，其他参数不变，这时声速剖面在水平方向上不发生变化，计算得到的出射时指向海面方向的4根本征声线的初始掠射角、方位角和传播时间见表2。可以看到声速剖面在水平方向上发生变化时，到达接收水听器的本征声线和传播时间发生了比较明显的变化。

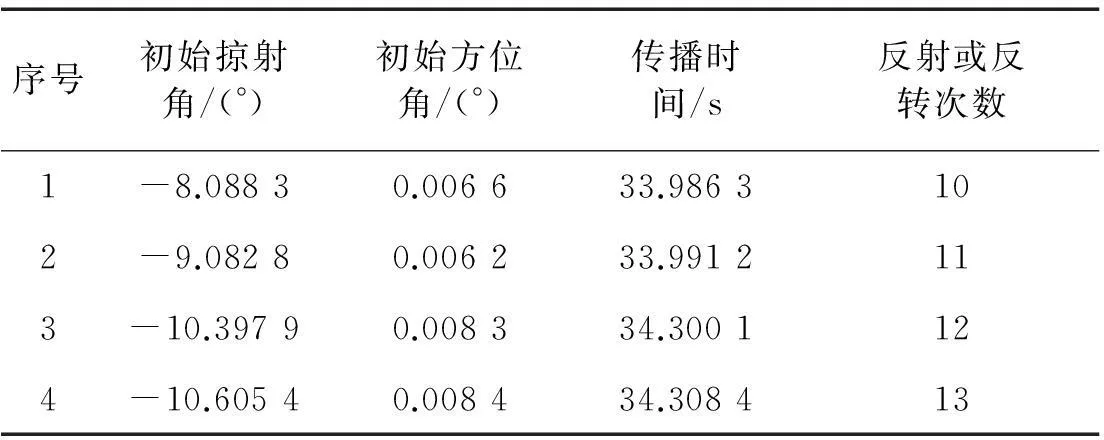
表1　本征声线的出射角和传播时间

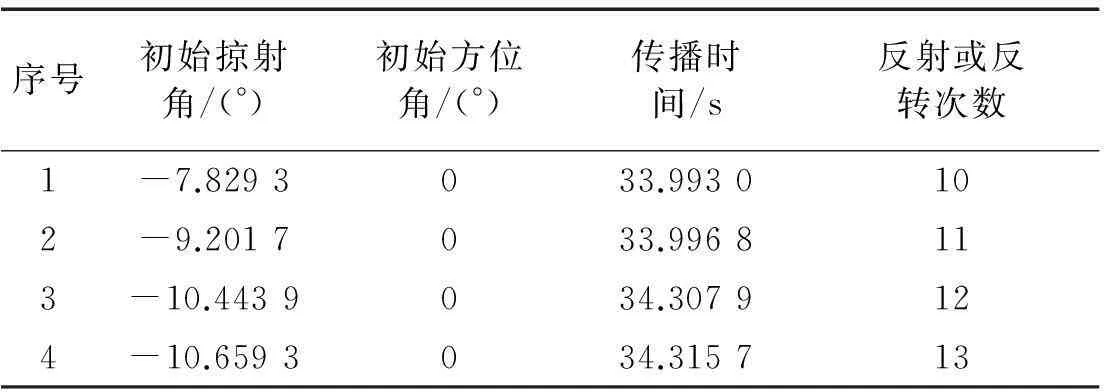
表2　本征声线的出射角和传播时间

取a11,a21,a12,a22,a13,a23均为0，海底深度函数h=800+0.001x+0.002y，其他参数不变，这时海底为倾斜海底，求取的本征声线的轨迹见图5，从图5可知，声线在水平方向上发生了偏转，海底深度在水平方向上的变化对求取的本征声线产生了明显的影响。

4结论

由于海洋环境参数随距离变化，这时海洋环境不能再看作是分层介质的情况。基于射线声学理论提出了一种非分层海洋中的声线计算方法，计算声线的轨迹和传播时间，求取到达接收水听器的本征声线，并进行了仿真计算。该方法用经验正交函数来表示声速剖面，适用于海水声速随距离的变化起伏程度不太大时，在一定范围的海域，将经验正交函数的系数近似为大致随水平距离线性变化，得出了声线轨迹的近似计算式。声线在海底反射点的位置用逐步迭代逼近法计算，可以用于计算任意海底深度变化的情况。该方法计算声线速度快，计算精度较高，具有较好的实用性。声速剖面用前几阶经验正交函数表示，用较少的参数就可以比较精确的表示海洋中的声速剖面，因此该方法可以用于声速剖面的快速反演。

参 考 文 献

[1] Lu I T. Simultaneous characterization of source,array and environment using a ray travel-time inversion approach [J]. J.Comput.Acoust, 1997,5(2):193-218.

[2] 孙枕戈，马远良，屠庆平，等. 基于声线理论的水声被动定位原理[J]. 声学学报，1996, 21(5): 824-831.

SUN Zhen-ge, MA Yuan-liang, TU Qing-ping, et al. Theory of passive localization for underwater sources based on acoustic ray modelling [J]. Acta Acustica, 1996, 21(5): 824-831.

[3] 齐娜，田坦. 多波束条带测深中的声线跟踪技术[J]. 哈尔滨工程大学学报，2003, 24(3): 245-248.

QI Na, TIAN Tan. Ray tracing in multi-beam swath bathymetry [J]. Journal of Harbin Engineering University, 2003, 24(3): 245-248.

[4] Georges T M,Jones R M,Riley J P. Simulating ocean acoustic tomography measurements with Hamiltonian ray tracing[J]. IEEE J. of Oceanic Engineering,OE-11,1986(1):58-71.

[5] 南明星，杨廷武，丁风雷. 海洋锋区的三维声线轨迹分析[J]. 声学技术，2003, 22(4):279-281.

NAN Ming-xing, YANG Ting-wu, DING Feng-lei. Three-dimensional ray tracing in ocean front region [J]. Technical Acoustics, 2003, 22(4):279-281.

[6] 姜薇，李太宝. 三维声线追踪的正三棱锥前向伸展算法[J]. 声学学报，2005, 30(5): 404-408.

JIANG Wei, LI Tai-bao. A three dimensional sound ray tracing method by deploying regular tetrahedrons [J]. Acta Acustica, 2005, 30(5): 404-408.

[7] 唐俊峰，杨士莪. 由传播时间反演海水中的声速剖面[J]. 哈尔滨工程大学学报，2006, 27(5):733-737.

TANG Jun-feng, YANG Shi-e. Sound speed profile in ocean inverted by using travel time [J]. Journal of Harbin Engineering University, 2006, 27(5):733-737.

[8] Tolstoy A, Diachok O, Frazer L N. Acoustic tomography via matched field processing [J]. J.Acous.Soc.Am, 1991, 89(3): 1119-1127.

[9] Yang S E. Theory of underwater sound propagation [M]. Harbin Engineering University Press, 2009.

[10] 王恕铨，Farmer D. 求解三维本征声线的一种新方法[J]. 声学学报，1992, 17(2): 155-157.

WANG Shu-quan, Farmer D. A new method of three-dimensional eigenray-tracing [J]. Acta Acustica, 1992, 17(2): 155-157.

[11] Mercer J A, Felton W J, Booker J R. Three-dimensional eigenrays through ocean mesoscale structure [J]. J. Acous. Soc. Am, 1985,78(1):157-163.

[12] 刘伯胜，雷家煜. 水声学原理[M]. 哈尔滨：哈尔滨工程大学出版社，2006.