解相关 EMD：消除模态混叠的新方法

第一作者 肖瑛 女，博士，副教授，1979年生

解相关EMD：消除模态混叠的新方法

肖瑛1,2， 殷福亮1

(1.大连理工大学 电子信息与电气工程学部，辽宁大连116024； 2. 大连民族学院 信息与通信工程学院，辽宁大连116600)

摘要：模态混叠是制约希尔伯特-黄变换(Hilbert-Huang Transform，简称HHT)在工程上推广应用的一个主要难题，采用在经验模态分解(Empirical Mode Decomposition，简称EMD)过程中嵌入解相关操作有效解决了EMD过程中产生的模态混叠问题。模态混叠的本质是各本征模态函数(Intrinsic Mode Function，简称IMF)分量之间信息相互耦合，无法表征有意义的物理过程，因此可认为模态混叠现象是由于IMF之间不完全正交导致。根据零均值随机信号正交性与不相关具有等价关系，在EMD过程中嵌入解相关操作，可有效保证IMF之间的正交性，消除模态混叠。仿真信号处理结果证明了方法的有效性。

关键词：经验模态分解；解相关；正交性；时频分析

基金项目：国家自然科学基金(61201418);中央高校基本科研业务费专项资金资助(DC12010218);辽宁省高等学校优秀人才支持计划(LJQ2013126)

收稿日期：2013-10-21修改稿收到日期：2014-02-25

中图分类号:TN957.52文献标志码： A

Decorrelation EMD: a new method of eliminating mode mixing

XIAOYing1,2,YINFu-liang1(1. Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China；2. College of Information and Communication Engineering, Dalian Nationality University, Dalian 116600, China)

Abstract:Mode mixing is one of difficulties of HHT in engineering applications. Here, a new method embedding a decorrelation operator into EMD process for solving mode mixing was proposed. The essence of mode mixing was mutual coupling of IMFs, it led to that a meaningful physical process could not be expressed with these IMFs, and it was considered that the mode mixing was due to that IMFs were not completely orthogonal. As the orthogonality and the non-correlation of a random process were equivalent, embedding a decorrelation operator into EMD process could improve the orthogonality of IMFs effectively and eliminate mode mixing. The simulation results showed the effectiveness of this method.

Key words: EMD; decorrelation; orthogonality; time-frequency analysis

希尔伯特-黄变换(Hilbert-Huang Transform，HHT)是1998年N.E Huang等提出的一种处理和分析非平稳信号的新方法[1]，近年来在故障信号检测、医学信号处理、地震信号分析等诸多领域得到了广泛应用[2]。但是到目前为止，理论基础、端点效应和模态混叠仍然是HHT方法没有完全得到解决的问题。在HHT的理论基础研究上，钟佑明等[3]做了大量的研究，初步为HHT提供了一个统一理论依据。端点效应比较有效地方法包括[4]：镜像闭合延拓法、极值点对称延拓法、神经网络法等。针对模态混叠问题，Huang提出了筛选预设尺度(极值点间距离)上限的方法来抑制模态混叠问题，但是并没有给出详细处理方法，Wu等[5]提出了集总经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法抑制模态混叠，对分解混有间断事件的信号产生的模态混叠具有很好的抑制效果，但是对小频率比混合信号产生的模态混叠效果不理想，同时为了使EEMD实现理想的分解结果，预先需要知道信号的信噪比。Ryan等[6]提出了掩膜信号法，通过对原始混合信号加减掩膜信号后分别利用EMD进行分解，并将对应IMF分量叠加的方法实现对模态混叠的抑制，对于小频率比混合信号进行EMD分解产生的模态混叠具有很好的抑制效果，但是对于不同的混合信号，掩膜信号的幅度和频率确定具有一定难度。陈建国等[7]提出了采用独立分量分析(Independent Component Analysis，ICA)方法进行模态混叠抑制，汤宝平等[8]进一步结合形态滤波降噪后进行峭度最大化的ICA方法进行模态混叠抑制，独立分量分析可有效提高EMD分解得到的IMF分量之间的正交性，但是ICA具有幅度不确定性和顺序不确定性，顺序不确定性对于信号特征提取和时频分析没有影响，但是幅度不确定性往往限制对信号能量信息的分析判断。高云超等[9]提出了差分运算、累积求和结合的方法进行模态混叠的抑制，通过差分运算放大高频分量引起的极值点，从而使得原本不满足EMD将多分量信号分解为单分量信号的充分条件得到满足，但是差分运算和累积求和运算本质上等效于低通滤波和高通滤波，因此在差分运算和积分运算中存在丢失某些信息的可能性。EMD分解过程具有带通滤波特性[10]，模态混叠产生的现象是分解得到的IMF分量之间的信息相互耦合，本质上可归结为IMF分量之间不完全正交。根据零均值随机信号之间不相关和正交性等价原理，提出了一种在EMD过程中嵌入解相关运算的改进方法，对于实际中均值不为零的信号，通过去趋势项和零均值化处理可以很容易满足均值为零条件，而事实上振动信号一般具有零均值特性。仿真结果证明解相关EMD(Decorrelation Empirical Mode Decomposition，DEMD)方法可以很好的保证IMF之间的正交性，达到抑制模态混叠的目的。

1HHT基本原理

HHT方法是Huang等在对瞬时频率的概念进行深入研究后提出的。HHT方法包括两个主要组成部分：EMD和希尔伯特变换(Hilbert Transform，HT)，主要思想就是将复杂的多分量混合信号分解为多个简单信号的合成形式。这些简单的信号称为IMF[11]，并且满足条件：① 在整个数据区间内，极值点的数目与过零点的数目相等或至多相差一个；② 在任意一点处，局部极大值点定义的包络以及由局部极小值点定义的包络的均值为0。在IMF定义基础上，HHT给出了瞬时频率合理的定义、物理意义和求法，建立了以瞬时频率表征信号交变的基本量，以IMF为基本时域信号的时频分析方法。对信号x(t)进行EMD可以表示为

(1)

式中：ci(t)为EMD得到的第i个IMF；rn(t)为分解余量，它表征了信号的平均趋势，通常是一个单调函数或者是只有一个极值点的函数。

HHT分别对每一个IMF分量用HT进行谱分析，对分解得到的IMF分量做HT可以得到

(2)

由此得到对应的解析信号

(3)

这样，幅值函数为

(4)

对应的相位函数为

(5)

进一步根据瞬时频率的定义可得

(6)

这样，对信号x(t)做整体的HT变换，x(t)在时频平面上就可以表示为

(7)

HHT借助于信号的IMF组合，幅值调制和频率调制被清晰地分离开来，跨越了Fourier变换仅对线性系统和平稳信号有效的不足之处，使得HHT能够成功地应用于非线性系统和非平稳信号的处理。式(7)的表示以时间t和瞬时频率ωi(t)为自变量，信号的幅值为时间t和瞬时频率ωi(t)的函数，这种幅值的时间-频率分布被称为Hilbert谱(也称为HHT谱)[12]，记作H(ω,t)。

从HHT进行时频分析过程可知，信号x(t)正确分解为IMF是保证HHT有效的前提。而EMD的分解过程是一种基于数据极值包络求均值曲线的一种局部自适应分解方法，因此对于EMD的正交性问题，Huang等认为在实际意义上是存在的，因为每个IMF分量都是上次分解到剩余信号与其均值的差，这个IMF分量与均值曲线是局部正交的，因此

(8)

但是，Huang的论证也只能说明IMF分量之间的正交性在实际物理意义上是满足的，并没有给出理论上的严格证明。并且这种正交关系并不一定严格成立，原因在于均值是通过包络求得的，所以它并不是真实的均值，而且每一个IMF分量只是信号包络均值的一部分。在这种情况下，EMD的能量泄露是不可避免的。对于EMD的全局正交性，HHT没有给出严格的理论证明，但是局部能量泄露已经可以说明EMD全局正交性也是难以保证的。

2EMD的模态混叠现象

EMD作为一种数据驱动的自适应分解方法，目的是将复杂的非平稳多分量信号分解为易于处理的具有内蕴物理意义的IMF。但是，在某些情况下，EMD往往得不到理想的分解结果，会产生模态混叠。模态混叠现象是指同一IMF分量包含了不同的尺度分量，这直接导致混叠的IMF缺乏足够的物理意义，致使后续的时频分布混淆[13]。

产生模态混叠的原因主要有：① 信号中存在噪声干扰，改变了信号原本的极值点分布；② 信号中含有间断高频弱信号的干扰；③ 混合信号中组合分量的频率过于接近。对于混合信号中组合分量频率接近产生的模态混叠问题，文献[14]给出了多分量信号到单分量信号可用EMD分解的条件，称为AFDE(Almost Fully Decomposed by EMD)条件，即对于由两个单分量构成的多分量信号而言，EMD能给保证正确分解的条件是：(a)其中一个单分量信号的瞬时频率不小于另一个单分量信号瞬时频率的2倍，即f1≥2f2；(b)两个单分量信号瞬时频率与幅度之积满足a1f1≥a2f2，其中a1和a2分别表示两个单分量信号的幅度。其中条件(a)是必要条件，联合条件(a)和条件(b)就构成了充分条件。当上述条件不满足的时候，即会产生模态混叠。无论是由于什么原因产生的模态混叠，其现象表征就是同一IMF分量中包含了不同尺度信息，即某一IMF分量中包含了其他IMF分量中的内容。产生这一现象的本质原因可以归结为EMD分解不满足全局正交性。

对于噪声影响产生的模态混叠，可以在进行EMD之前进行降噪预处理，文中不作讨论。这里只讨论混合信号中组合分量信号不满足AFDE条件和信号中存在间断性高频弱信号产生的模态混叠问题。

仿真信号1：以仿真信号说明EMD在不满足AFDE条件时产生模态混叠现象，仿真信号1采用两正弦信号叠加生成，采样频率fs=1 000 Hz，两正弦信号的中心频率分别为f1=50 Hz，f2=80 Hz。

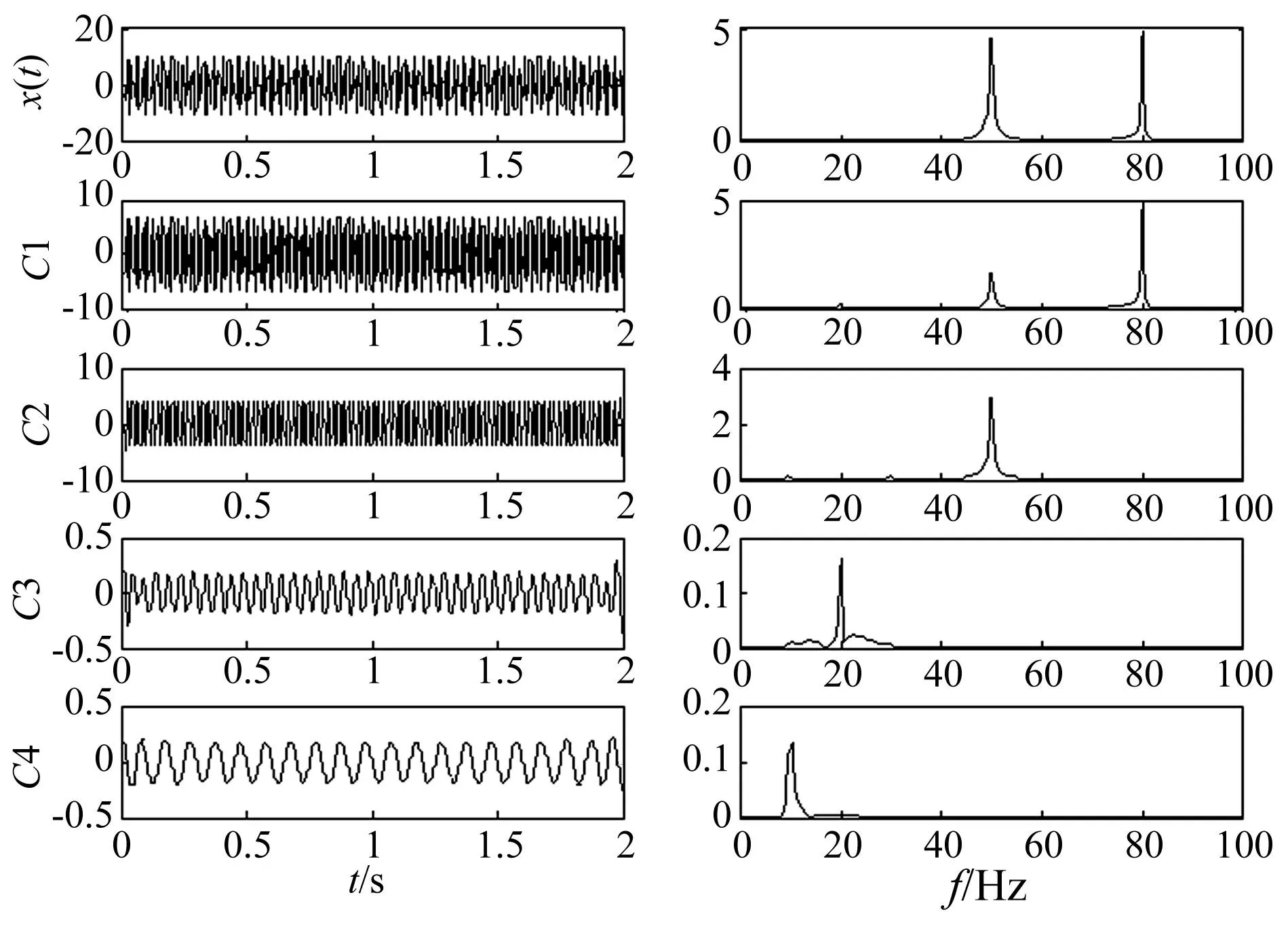
图1　仿真信号1的EMD结果 Fig.1 EMD results of simulation signal 1

(9)

显然x(t)不满足AFDE条件。图1给出了仿真信号x(t)的EMD结果及其频谱，两个正弦信号叠加的合成信号经EMD得到了C1～C4个IMF和一个残余分量r，其中C3～C4并没有实际物理意义，为虚假分量。而在分量C1中，尺度跨越了两个正弦信号分量的频率，在包含了f2=80 Hz的分量同时包含了部分f1=50 Hz的成分，产生了模态混叠。

仿真信号2：利用仿真信号说明信号中含有间断高频弱信号的干扰时，EMD产生模态混叠现象。仿真信号2利用正弦信号叠加生成，采样频率fs=1 000 Hz，两正弦信号的中心频率分别为：f1=10 Hz，f2=100 Hz，仿真信号如式(10)所示。图2给出了仿真信号的EMD结果和对应频谱，EMD在混合信号中含有间断高频弱信号的情况下，无法正确分解，C1中包含了间歇性高频弱信号和低频正弦信号，C2的波形严重失真，产生了模态混叠。

x(t)=x1(t)+x2(t)+x3(t)

(10)

式中:

(11)

图2　仿真信号2的EMD结果 Fig.2 EMD results of simulation signal 2

3解相关EMD

EMD产生模态混叠的根本原因可以归结为EMD过程不是严格正交分解，因此导致IMF之间信息相互耦合。尤其是在上述特殊情况下，这种非正交分解体现的尤为明显。为此可认为，保证IMF之间的正交性，是抑制模态混叠的一个有效方法。定义两随机变量x和y，其相关函数为

Cxy=E{(x-ηx)(y-ηy)}=

E{xy}-E{x}E{y}

(12)

式中：ηx=E{x}，ηy=E{y}，如果Cxy=0，则称x和y是不相关的。如果E{xy}=0，则称x和y是正交的。显然，如果x和y是不相关的，并且有ηx=0，ηy=0，那么x和y是正交的，因此对于零均值随机变量而言，不相关和正交具有等价性。对于EMD而言，待分析信号大部分满足零均值特性，典型的如振动信号、冲击信号等，即使待分析信号的均值不为零，仍然可以通过中心化处理使之满足零均值特性。因此保证IMF之间的正交性，可以通过解相关算法进行处理。根据解相关算法定义相关系数为

(13)

显然，ry(n)代表了x(n)中与y(n)相关的部分，如果从x(n)中减去这一部分，就得到了与y(n)不相关的部分，表示为：

v(n)=x(n)-ry(n)

(14)

(15)

对比式(13)和式(15)可知

(16)

因此，r只是归一化相关系数rN的比例缩放，并不影响解相关方法的处理结果。

基于上述分析，我们设计一种解相关EMD方法，步骤如下：

步骤1：对待分析信号x(t)利用EMD得到M个IMFci(t)；

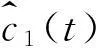
步骤4：重复步骤2和步骤3直到所有IMF分量间相关系数小于设定的阈值δ。

经过在EMD过程中嵌入解相关算子，可以有效的保证分解得到的IMF分量之间的正交性，从而达到抑制模态混叠的目的。同理，该方法可以推广应用到EEMD过程中。

4仿真分析

对由式(9)和式(10)给出的仿真信号进行处理，处理过程中设定相关系数阈值δ=0.001。处理结果分别如图3和图4所示。从图3可知，通过在EMD过程中嵌入解相关算子，使得小频率比混合信号EMD的模态混叠现象得到了有效抑制，并且分解未产生冗余分量。从图4可知，在EEMD过程中嵌入解相关操作，进一步提高了EEMD的分解性能，抑制模态混叠的同时没有冗余分量的产生。为了进一步说明解相关EMD的性能，根据文献[14]定义的标准均方误差NMSE对算法性能进行分析。

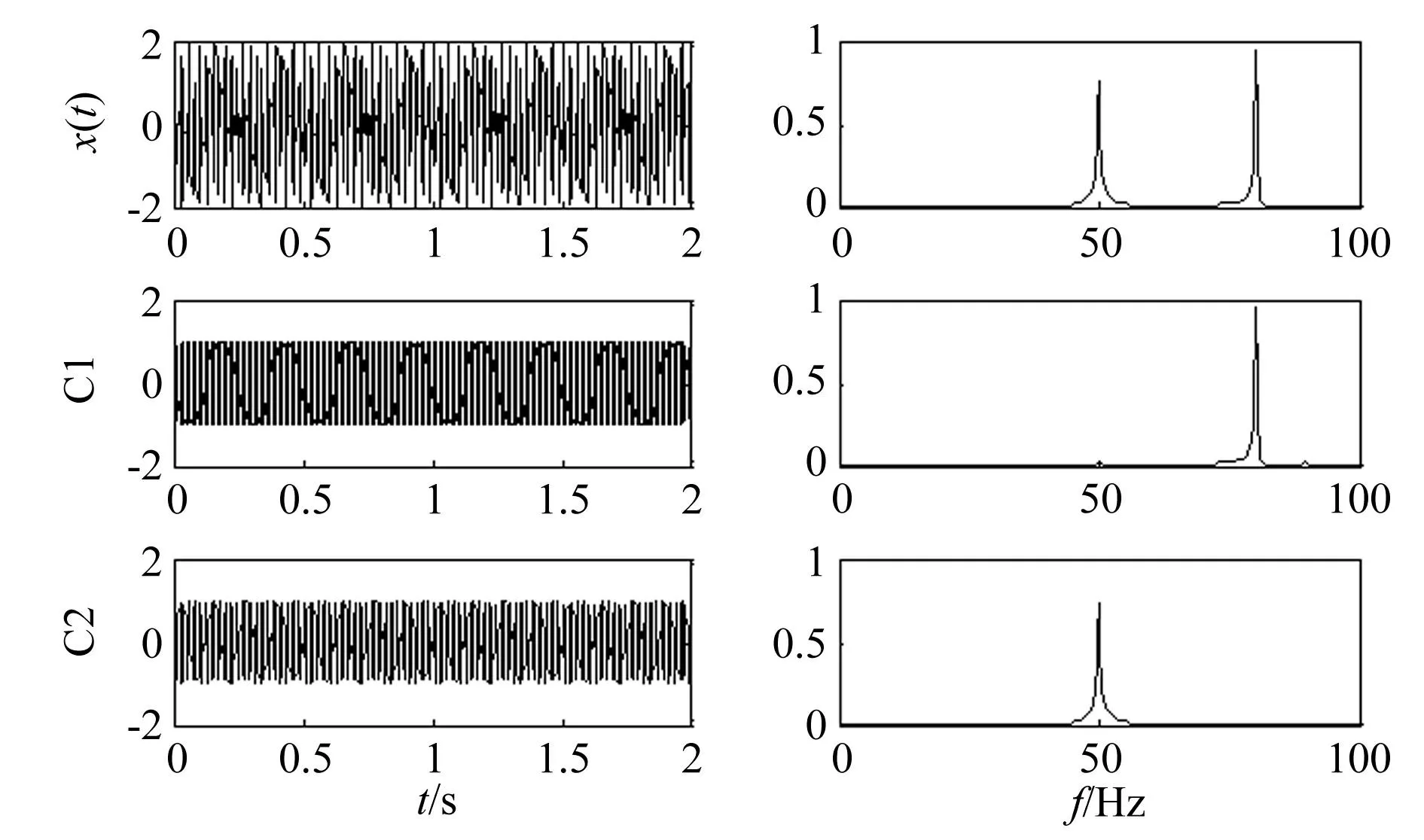
图3　仿真信号1的DEMD结果 Fig.3 DEMD results of simulation signal 1

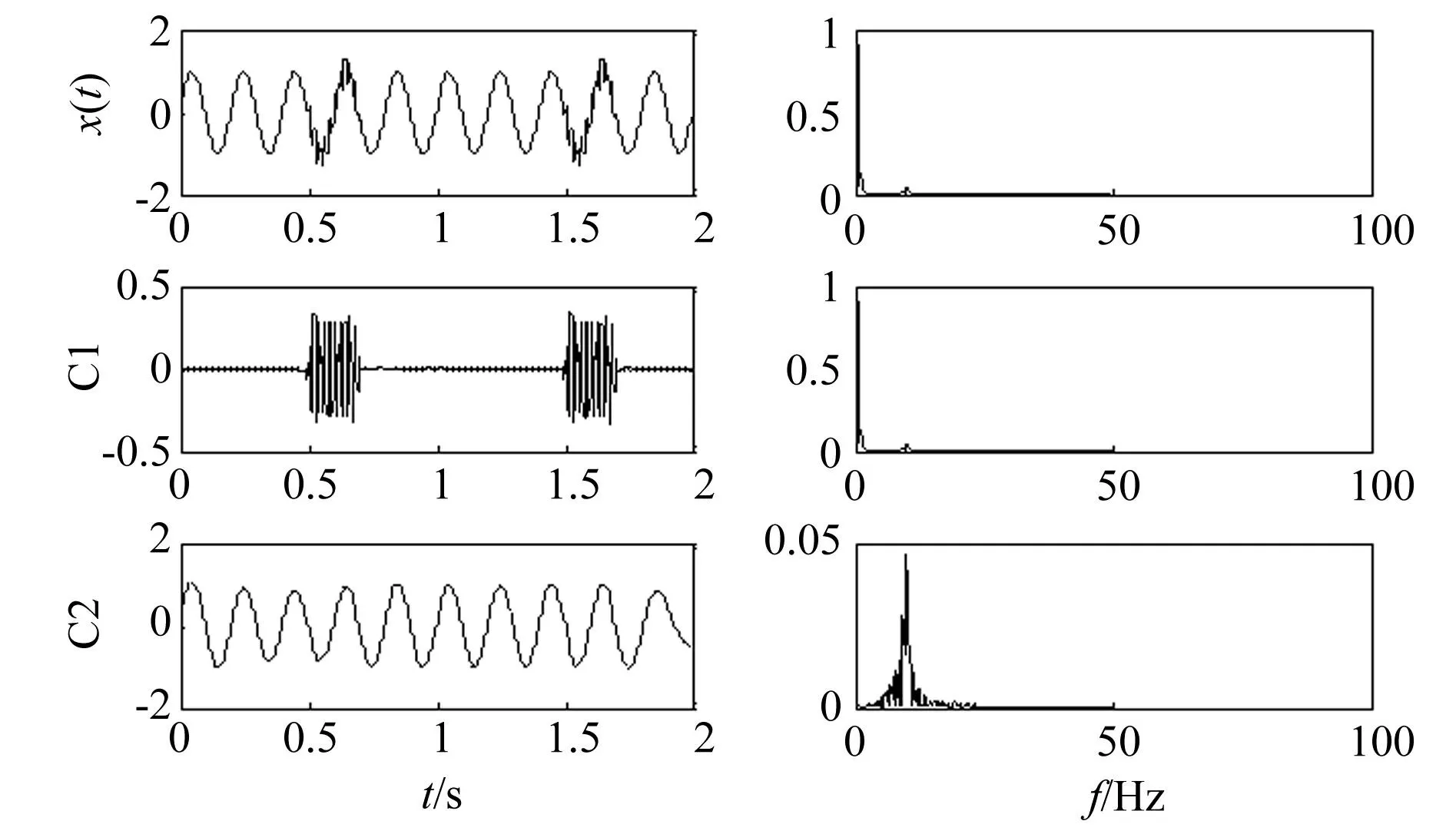
图4　仿真信号2的DEEMD结果 Fig.4 DEEMD results of simulation signal 2

(17)

(18)

式中：fi(t)为与ci(t)对应的混合信号中的单分量信号，仿真信号1和仿真信号2对应的NMSE如表1所示。从表1中可以看出，解相关EMD(DEMD)具有更好的分解性能。

表1　NMSE比较结果

5结论

在分析EMD模态混叠现象的基础上，通过在EMD过程中嵌入解相关操作，保证了IMF分量之间的正交性，给出了一种抑制模态混叠的新方法。对小频率比混合信号和间断性高频弱信号干扰的混合信号进行了仿真处理，并对直接EMD，EEMD和DEMD的性能进行了比较，验证了解相关EMD方法的有效性。

参 考 文 献

[1] Huang N E, Shen Z, LONG S R, et al. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis [J]. Proceedings of the Royal Society A, 1998(454): 903-995.

[2] 贾春花. 希尔伯特-黄变换及其在信号处理中的应用研究[J]. 电力学报, 2013, 28(2): 148-151.

JIA Chun-hua. Study of hilbert-huang transform and its applications in signal processing [J]. Journal of Electric Power, 2013, 28(2): 148-151.

[3] 钟佑明, 秦树人. 希尔伯特-黄变换的统一理论依据研究[J].振动与冲击, 2006, 25(3): 40-43.

ZHONG You-ming, QIN Shu-ren. Research on the uniform theoretical basis for hilbert-huang transform (HHT) [J]. Journal of Vibration and Shock, 2006, 25(3): 40-43.

[4] 杜陈艳, 张榆锋, 杨平，等. 经验模态分解边缘效应抑制方法综述[J]. 仪器仪表学报, 2009, 30(1): 55-60.

DU Chen-yan, ZHANG Yu-feng, YANG Ping, et al. Approaches for the end effect restraint of empirical mode decomposition algorithm [J]. Chinese Journal of Scientific Instrument, 2009, 30(1): 55-60.

[5] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[6] Ryan D, James F K. The use of a masking signal to improve empirical mode decomposition [C]. International Conference on Acoustics, Speech, and Signal Processing (ICASSP), IEEE, 2005:485-488.

[7] 陈建国, 张志新, 郭正刚等. 独立分量分析方法在经验模态分解中的应用[J]. 振动与冲击, 2009, 28(1): 109-111.

CHEN Jian-guo, ZHANG Zhi-xin, GUO Zheng-gang, et al. Application of independent component analysis in empirical mode decomposition [J]. Journal of Vibration and Shock, 2009, 28(1): 109-111.

[8] 汤宝平, 董绍江, 马靖华. 基于独立分量分析的EMD模态混叠消除方法研究[J]. 仪器仪表学报, 2012, 33(7): 1477-1482.

TANG Bao-ping, DONG Shao-jiang, MA Jing-hua. Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis [J]. Chinese Journal of Scientific Instrument, 2012, 33(7): 1477-1482.

[9] 高云超, 桑恩方, 许继友. 分离EMD中混叠模态的新方法[J]. 哈尔滨工程大学学报, 2008, 29(9): 963-966.

GAO Yun-chao, SANG En-fang, XU Ji-you. A new method for separating mixed modes in empirical mode decomposition [J].Journal of Harbin Engineering University, 2008, 29(9): 963-966.

[10] 孙世钧, 李秀坤. 经验模态分解WVD方法的水下目标特征提取[J]. 哈尔滨工程大学学报, 2013, 34(8):1-4.

SUN Shi-jun, LI Xiu-kun. Underwater target feature extraction using empirical mode decomposition and WVD method [J]. Journal of Harbin Engineering University, 2013, 34(8):1-4.

[11] 刘强, 周瑞忠, 刘宇航. 基于HHT变换的结构地震响应与能量计算分析[J]. 武汉大学学报：工学版, 2009, 42(6): 780-784.

LIU Qiang, ZHOU Rui-zhong, LIU Yu-hang. Computation and analysis of seismic response and energy based on hilbert-huang transform [J]. Journal of Wuhan University:Engineering, 2009, 42(6): 780-784.

[12] 公茂盛, 谢礼立. HHT方法在地震工程中的应用之初步探索[J]. 世界地震工程, 2003, 19(3): 295-299.

GONG Mao-sheng, XIE Li-li. Discussion on the application of HHT method to earthquake engineering [J]. World Earthquake Engineering, 2003, 19(3): 295-299.

[13] 赵玲, 刘小峰, 秦树人,等. 消除经验模态分解中混叠现象的改进掩膜信号法[J].振动与冲击, 2010, 29(9): 13-17.

ZHAO Ling, LIU Xiao-feng, QIN Shu-ren et al. Use of masking signal to improve empirical mode decomposition [J]. Journal of Vibration and Shock, 2010, 29(9): 13-17.

[14] 徐冠雷, 王孝通, 徐晓刚,等. 多分量到单分量可用EMD分解的条件及判据[J]. 自然科学进展, 2006, 16(10): 1356-1360.

XU Guan-lei, WANG Xiao-tong, XU Xiao-gang et al. The conditions and criteria of multi-component decompose into single component by EMD[J]. Progress in Natural Science, 2006, 16(10): 1356-1360