一种改进的FCM算法及仿真实验研究

一种改进的FCM算法及仿真实验研究

刘杰

(陕西理工学院 数学与计算机科学学院， 陕西 汉中 723000)

[摘要]针对模糊C均值(FCM)算法的缺陷，提出了一种改进的FCM算法。将物理学中的信息熵概念引入聚类分析中，用熵值法度量样本的各种属性对分类不同程度的影响，并用模糊划分系数FC(μ)和平均模糊熵HC(μ)对改进后的算法性能进行了评价。仿真实验结果表明，改进后算法的FC(μ)和HC(μ)分别为0.919和-0.096，改进后的FCM算法在实际的聚类分析中能取得更好的分类效果。

[关键词]模糊C均值算法；改进；信息熵；模糊划分系数；平均模糊熵

[文章编号]1673-2944(2015)04-0040-05

[中图分类号]TP301.6

收稿日期：2014-11-07

基金项目：陕西省科技厅重大科技创新专项(2011ZKC05-16)；陕西省教育厅科学研究计划项目(12JK0982)

作者简介：刘杰(1982—)，女，陕西省汉中市人，陕西理工学院讲师，硕士，主要研究方向为智能算法及应用。

聚类就是按照一定的要求和规律对事物进行区分和分类的过程。聚类分析是多元统计分析的一种，它将没有类别标记的样本按照某种准则划分成若干子集，使相似的样本尽可能归为一类，而不相似的样本尽量划分到不同类。由于在该过程中没有任何关于分类的先验知识而仅靠事物间的相似性作为类属划分的准则，因此属于无监督分类方法。该方法已经被广泛应用于模式识别、数据挖掘及图像处理等各个领域。

传统的聚类分析是一种硬划分，将每一个样本严格地归属于某一类中，具有非此即彼的绝对性，分类界限明确。而在实际的分类中，很多对象在性态和类属方面具有中介性，那么采用硬划分的方法就因为出现争议而缺乏合理性，因此通常采用软划分。Zadeh提出的模糊集理论为这种软划分提供了重要的理论依据，通过度量样本属于各类别的不确定性程度来描述样本类属的中介性，更客观地反映现实世界，最终实现样本的模糊聚类分析。在各种模糊聚类算法中，Bezdek于1973年提出的FCM(模糊C均值，Fuzzy C-Means)聚类算法是非监督模式识别中最经典且应用最广泛的算法[1]。该算法通过隶属度来描述每个样本属于某个聚类的程度，并利用极小化目标函数求得最优解较好地实现了空间聚类[2-3]。但是FCM算法也存在自身的缺陷：算法事先假设待分类样本的各项属性对分类的贡献相同，忽略了各种属性对分类的不同程度的影响[4]。基于这一点，本文提出了一种FCM算法的改进方法，通过信息熵权重来度量样本各项属性对分类的影响，将该权重引入到FCM算法中。为了验证改进后算法的有效性，通过具体实例进行仿真实验。

1经典的FCM算法

设待划分的样本集X={X1,X2,…,Xn}，n为样本个数，聚类的类别数为C，则有C个聚类中心V=(v1,v2,,…,vC)，其中2≤C≤n，则n个样本对应于C个类簇的隶属矩阵表示为：

(1)

其中μij代表第j个样本属于第i类的隶属度。并且它满足以下几个条件：

(2)

(3)

(4)

经典FCM算法的基本思想是同一类簇中的样本之间的距离尽可能最小，而不同类簇中样本的距离尽可能的大。算法采用的具体步骤如下：

Step 1：由用户给定聚类的数目C；

Step 2：随机选择C个样本，选出的每一个样本被称为一个种子，代表一个类的均值或中心；

Step 3：将剩余的每个样本赋给离它最近的类；

Step 4：重新计算每个类中样本的平均值，形成新的聚类中心；

Step 5：判断新的聚类中心是否和上次的完全相同，若相同则算法停止，否则返回到Step3。

将该算法表示为极小化的目标函数为：

(5)

其中vi为每一类的类簇中心；(xj-vi)2表示第j个样本Xj到第i类类簇中心vi的欧氏距离；m为加权指数，它的最佳取值范围为[1.5，2.5]，Bezdek在研究中发现m=2时具有明确的物理意义[5]。

由拉格朗日算法联合式(4)，可得类簇中心vi和隶属度μij的迭代公式为：

(6)

(7)

2改进的FCM算法

由于FCM算法事先假设待分类样本的各项属性对分类的贡献相同，忽略了各种属性对分类的不同程度的影响。基于这一点，本文提出基于属性信息熵权重的FCM改进算法。

2.1信息熵

“熵”是德国物理学家克劳修斯于1850年提出的概念，是热力学和统计物理学中特有的宏观量，它用来表示任何一种能量在空间中分布的均匀程度。信息论之父C.E.Shannon在1948年发表的论文《通信的数学理论》中将熵的概念引入信息论，称为“信息熵”。系统的熵值直接反映了它所处状态的均匀程度。个体之间越是接近，表示他们的差异越不显著，熵值就越大，反之，个体差异越明显其熵值就越小[6]。

(8)

2.2熵值法确定权重

根据信息熵理论，信息熵是信息不确定性的度量，若某个属性的熵值越小，则说明该属性在决策时所起的作用越大，应赋予该属性较大的权重。即可以用熵值法来确定样本各属性的权重[8]。对于给定样本集的第s项属性，若该属性的信息熵值越大，则表示样本间该属性的差异性越小，那么其表示该属性在决定样本分类时所起的作用就越小。相反的，若该属性的信息熵值越小，那么其表示该属性在决定样本分类时所起的作用就越大。根据属性的熵值大小ej与该属性下的分类归属相反的原则，定义属性s的差异因数即偏差程度系数为：

(9)

当gs越大时，第s项属性就越重要，那么假设样本集有z项属性，用差异性因数gs来确定第s项属性的权重：

(10)

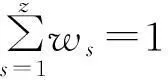
2.3基于信息熵权重的FCM改进算法

设第j个样本Xj有z个属性，记为Xj=(xj1，xj2，…，xjz)，1≤j≤n。根据信息熵值法得到的属性权重为W=(w1，w2，…，wz)，将经典的FCM算法进行改进如下：

(11)

基于该改进算法的类簇中心vi和隶属度μij的迭代公式为：

(12)

(13)

3实例仿真

3.1实验数据

以汉江水源地汉中市的水污染物COD分配为例，采用改进后的FCM算法对汉中市的11个行政区域水污染物削减程度进行分类，依据各区域的经济环境发展情况和COD的排放量将各个行政区域归属为重点削减区域、加强削减区域和普通削减区域3大类。

选取2010年汉中市11个行政区作为样本集，区域水资源量、区域水环境容量、区域人口、区域生产总值(GDP)为样本集的4项属性，样本集及其属性数据如表1所示(数据均来自于《2010年汉中市统计年鉴》和《2010年汉中市环保局环境统计公报》)。

表1　2010年汉中市各县区社会经济环境指标

续表

3.2数据归一化处理

为了消除不同量纲对结果的影响，先对表1中的基础数据按照式(14)进行归一化处理：

(14)

式中xjs表示第j样本的第s项属性值，minxs和maxxs分别表示所有样本第s项属性的最小值和最大值。

3.3计算各属性的权重

按照本文2.2中的熵值法计算出样本数据的4项属性的权重如表2所示。

表2　样本各项属性的权重

3.4两种算法的聚类结果

采用以上实验数据分别利用两种算法对该问题进行聚类。在两种算法中，分类数C=3，分别表示重点削减A类、加强削减B类和普通削减C类。样本数n=11，加权指数m=2，FCM算法采用式(5)，迭代方式采用式(6)和(7)，改进的FCM算法采用式(11)，迭代方式采用式(12)和(13)。利用Matlab进行算法实现，得到如表3的分类结果。

表3　两种算法的分类结果

3.5改进的FCM算法的性能评价

为了判定改进后的FCM算法的性能，引入聚类分析算法中的两个主要性能指标，即模糊划分系数FC(μ)和平均模糊熵HC(μ)：

(15)

(16)

分别计算两种算法的两个性能指标，计算结果如表4所示。

表4　两种算法的性能指标

从表4中可以看出，在该应用中，改进后的FCM算法的模糊划分系数和平均模糊熵两项主要的性能指标都比FCM原型算法有所增大。从表1的基础数据不难看出，汉台和城固两个区域的水资源量和环境容量仅占全市的6.7%和5.6%，水污染物COD的排放量却占到全市总量的23%，尤其是汉台区的水资源量仅仅占0.7%，COD排放量却占到全市的6%，因此这两个区域属于重点削减区域。其次，勉县和洋县两个区域占全市16%的环境容量，却占全市30%的COD排放量，属于加强削减区域。其余的7个区域均属于普通削减区域。该分类结果与实际情况和实际需要更加相符。从该实验的分类结果来看，改进后的FCM算法考虑了各属性在聚类分析中的影响程度，在实际应用中能更切实际地进行类属的划分。

4结论

改进后的FCM算法克服了在分类时属性对分类结果的影响，在原型算法中增加了属性权重的因素，利用属性的信息熵反映并度量属性在分类时的重要性，采用熵权法确定各属性权重，同时对迭代过程中类簇中心和隶属矩阵的更新做出了相应的修正。数据的仿真实验证明改进后的算法分类能更好地反映客观现实。

[参考文献]

[1]KONG Yue-ping,ZENG Ping.A robust method for inverse halftoningvia 2-D nonlinear pyramid[J].Chinese Optics Letters,2007,5(11):573-576.

[2]肖春景,张敏.基于减法聚类与模糊C-均值的模糊聚类的研究[J].计算机工程,2005(31):135-137.

[3]孙惠琴,熊璋.改进的FCM算法及其在脑电信号处理中的应用[J].重庆大学学报:自然科学版,2014,37(6):83-88.

[4]张翡,范虹,郝艳荣.结合非局部均值的快速FCM算法分割MR图像研究[J].计算机科学,2014,41(5):304-307.

[5]BEZDEK J C.A Physical Interpretation of Fuzzy ISODATA[J].IEEET rans SMC,1976,6(3):387-390.

[6]黄定轩.基于客观信息熵的多因素权重分配方法[J].系统工程理论方法应用,2003,12(4):321-324.

[7]许友权,吴陈,杨习贝.初始聚类中心优化的加权最大熵核FCM算法[J].计算机系统应用,2014,23(8):139-143.

[8]朱方霞,陈华友.确定区间数决策矩阵属性权重的方法——熵值法[J].安徽大学学报:自然科学版,2005,30(5):4-6.

[责任编辑：谢 平]

An improved FCM algorithm and its simulation experiments

LIU Jie

(School of Mathematics and Computer Science, Shaanxi University of Technology,

Hanzhong 723000, China)

Abstract:Considering the defects of the traditional Fuzzy C-Means (FCM) algorithm, an improved FCM algorithm has been proposed in this paper. The information entropy which is the concept of the physics is introduced into the fuzzy cluster analysis and the entropy evaluation method is used to measure the varying degree of influence of the various attributes in cluster analysis. At the same time, the fuzzy division coefficient FC(μ) and the average fuzzy entropy HC(μ) are used to evaluate the performance of the improved FCM algorithm. The simulation results show that the FC(μ) and the HC(μ) are 0.919 and -0.096 respectively which show that the improved FCM algorithm can obtain better classification effect than the traditional FCM algorithm in practical application.

Key words:Fuzzy C-Means algorithm;improve;information entropy;fuzzy partition coefficient;average fuzzy entropy