圆管分层两相流问题的解析方法
2016-01-16卢天祥,张劲柏
圆管分层两相流问题的解析方法
卢天祥1,张劲柏2
(1.北京航空航天大学 中法工程师学院,北京100083;2.北京航空航天大学 航空科学与工程学院,北京100083)
摘要:管道输运工程中经常遇到两相流问题,因此需要预测对流体施加的压力大小以指导运输。拟对圆直管道分层两相流-层流模型做研究,用解析方法计算出圆管任一截面处流体的速度分布,并验证两层流体交界面处的摩擦力与其平均速度差值呈近似线性关系的结论。以此为基础,可以通过计算截面速度分布得到流体与管壁的摩擦力,通过输运流体所需达到的速度得到分界面处摩擦力,最终反推出运输流体所需要施加的压力差大小。
关键词:两相流;解析方法;平均速度差值;层间摩擦力
文章编号:1672-6758(2015)01-0061-3
中图分类号:O359`+.1
文献标识码:A
Abstract:Two-phase flow is usually encountered in pipe transport industry, hence the transport pressure needs to be forecasted for guiding the transport. This article studied a stratified two-phase flow in straight pipe model, calculated the velocity distribution in pipe section, and then verified that approximately, a linear relation exist between the interlayer friction of the two fluids and their average velocity difference. Based on that, friction between the fluids and the pipe can be obtained by the velocity distribution in pipe section, and the interlayer friction can be obtained by the expected transport velocity, and the transport pressure can be inferred at last.
流体输运工程中,经常出现两种或多种流体一同被输运的情况(如水/原油,原油/天然气,水/空气等),在层流状态,这些流体由于密度不同而分层分布;或由于受到干扰,产生脉动而呈混合状态分布。
国内外对于层流或湍流两相流问题的研究不在少数,[1][2][3][4]主要研究方法为实验方法,原因是两相流状态太多(可以大体归结为14种[5]),计算方法无法为其建立合适的方程,求解过程也过于复杂。但是实验方法有其很明显的弱点:易受外界条件干扰,不能根据需要灵活改变实验控制参数,成本太高等。针对这些弊端,研究人员开始对简单问题用计算方法处理,并开发出许多数值计算工具,其中石油业最为突出,计算软件有OLGA,[6]PLAC,TICITE,TUFFP等。
本文将研究一种简单层流模型—圆直管双层流动模型,两层流体无掺混,各自保持在层内稳定流动并达到稳态。由于两种流体的动力粘度不同,在交界面处会出现粘度奇点,因此,本文适用于研究两层流体粘度差值不大的情况,以忽略粘度差异对层间摩擦造成的影响,粘度差异大的情况会在后续另一篇论文中加以研究。
本文将给出模型的控制方程与边界条件,给出一种数学解析求解方法,求出圆管任一横截面处的流场,接下来计算两层流体的平均速度值与层间摩擦力,进而得出其近似关系。得知此关系后,便可以对输运所需要的压力进行有效地预测。
一控制方程及解析方法
图1为两相流模型示意图,其中,r为圆管半径(忽略管壁厚度),在此默认为1,φ为圆管倾角。图2为圆管截面示意图,分界面距离圆心Rcosθ0,r为积分半径,范围0-R,θr为积分角,上下层流体的动力粘度分别为μ1和μ2。

图1 两相流模型示意图

图2 圆管截面示意图
由流体连续性方程与动量定理,上下两层流体的控制方程均可表述如下:
(1)
式中,u为流体速度,ρ为流体密度,g为重力加速度,dP/dx代表沿x方向的压降。
本文采用无滑移边界条件:∀θ,u(r=1)=0;
由于流体处于稳态,对于给定的x=X,dP/dx为常值(最终目的即预测此项),因此,对于给定的两种流体,(dP/dx+ρ1gsinφ)/μ1与(dP/dx+ρ2gsinφ)/μ2均为常值,把它们分别记为C1和C2,为简化计算,把控制方程的解分解为:
u=(C1-C2)u1+C2u2
(2)
式中的u1和u2满足以下方程:
(3)
(4)
(4)式为一般二次偏微分方程,根据边界条件,可以得到其解为:
(5)
(5)式与θ无关,其实(4)表示的是泊肃叶流动,下面主要把精力放在解(3)式上。
对(3)式作傅立叶分解:
(6)
(6)式的解可表示为:
(7)
把(7)代入(6)并化简得到(cosnθ可以被单独拿出):
(8)
(9)
对于(8),令u'10(r)=f(r),代入(8)并在等号两侧同时乘以r,得到:
(10)
由(10)可得f(r),并进一步得到:
(11)
对于(9)式,令u1n(r)=f(r)·rn(n=1,2…),代入(9)并在等号两侧同时乘以rn+1,得到:
(12)
再令g(r)=f '(r),代入(12)并化简,得到:
(13)
由此积分可得到g(r),然后积分得到f(r),并进一步得到:
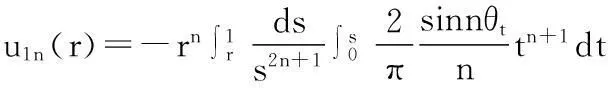
(14)
因此,(3)式的解析解为:
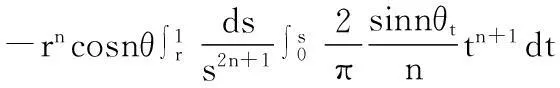
(15)
合并(2)(5)(15)式,控制方程最终解为:
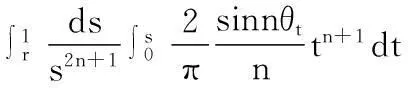
(16)
(16)式直接积分较为复杂,因此使用数值积分方法直接计算积分,选用结构化网格,每个R上分配10个点,每个θ分配30个点,并用Fortran语言编写程序。对于密度ρ1=1.24,ρ2=1000,粘度μ1≈μ2=1.3×10-3的两种流体,在C1=0.3,C2=0.7的情况下,截面处流场计算结果如下:
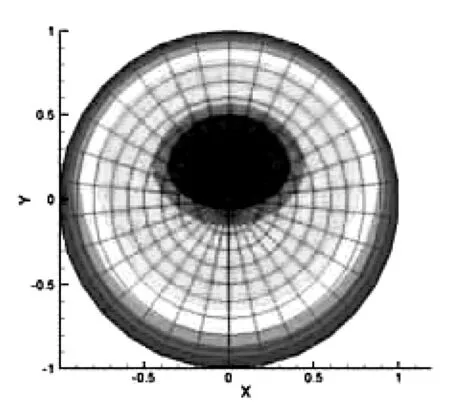
图3 截面流场分布图
二层间摩擦力
本节用于研究层间摩擦力与平均速度差值之间的关系。
先计算层间摩擦力,在圆管中选取一小段流体受力分析,根据动量守恒:

图4 微元受力示意图
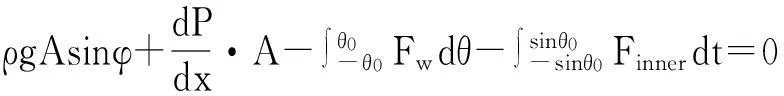
(17)


(18)
由(18)可得到层间摩擦力积分:
(19)
下面计算两层间的平均速度差值:
记上下层流体的流量分别为Fup和Fdown,因此:
(20)
(21)
记上下层截面积分别为Aup和Adown,于是上下层流体的平均速度可表示为:
(22)
(23)
平均速度差值:
(24)
由(20)(21)(24)式,即可得到上下层流体的平均速度差值。
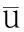

图5 λ=0.1时f- diff图
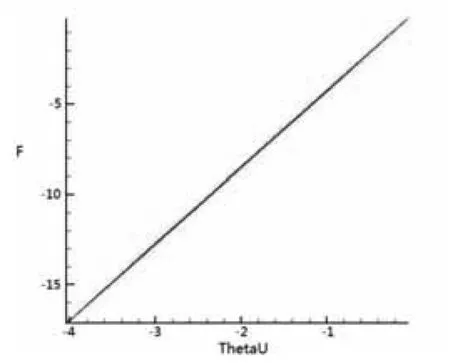
图6 λ=0.5时f- diff图

图7 λ=0.9时f- diff图
三结论
圆直管道分层两相流模型中,上下两层流体的层间摩擦力随着两层间平均速度差值呈近似线性的变化,并且对于两流体不同分界面位置,这个线性关系的斜率不同。
因此,在工程应用中,可以通过计算多种分界面情况下线性关系的斜率,做出工程手册。实际应用时,首先用查手册的方式得到斜率,根据工程需要的上下层流体的输运平均流速,计算出两层间的摩擦力;然后根据本文中截面处任意点的速度公式(16),得到流体与圆管壁面的摩擦力(关于输运压强P的函数),最终反推出流体的输运压强P,实现对流体输运工程的预测。
参考文献
[1]Kawahara A, Chung P M Y, Kawaji M. Investigation of Two-phase Flow Pattern, Void Fraction and Pressure Drop in a Microchannel[J]. International Journal of Multiphase Flow, 2002, 28(9): 1411-1435.
[2]Kenji YOSHIDA,Koichi KOND and Isao KATOAKA. Two-phase Flow Structure of Bubbly Flow in Round Tube with Sudden Expansion[R]. ISSNP2008 CSEPC ISOFIC2008, 2008: 179-185.
[3]刘文红, 郭烈锦, 张西民, 等. 水平直圆管内油气两相流的压降[J]. 化工学报, 2004, 55(6): 907-912.
[4]Mishima K, Hibiki T. Some Characteristics of Air-Water Two-Phase Flow in Small Diameter Vertical Tubes[J]. International Journal of Multiphase Flow, 1996, 22(4): 703-712.
[5]吴铁军, 郭烈锦, 刘文红, 等. 水平管内油水两相流流型及其转换规律研究[J]. 工程热物理学报, 2002.
[6]Bendiksen K H, Maines D, Moe R, et al. The Dynamic Two-fluid Model OLGA: Theory and Application[J]. SPE Production Engineering, 1991, 6(02): 171-180.
Analytical Method for Pipe Stratified Two-phase Flow Problem
Lu Tianxiang1, Zhang Jinbai2
(1.Sino-French Engineer School, Beihang University, Beijjing 100083, China)
2.School of Aeronautic Science and Engineering, Beihang University, Beijjing 100083, China)
Key words:two-phase flow; analytical method; average velocity difference; interlayer friction
Class No.:O359+.1Document Mark:A
(责任编辑:郑英玲)
