基于样本变异系数的Gamma分布参数估计

陈　超,孟昭为

(山东理工大学 理学院, 山东 淄博 255049)

基于样本变异系数的Gamma分布参数估计

陈超,孟昭为

(山东理工大学 理学院, 山东 淄博 255049)

摘要：Gamma分布的参数估计问题在数学中占有非常重要的地位.借助矩估计通过样本变异系数独立性构造了Gamma分布的形状参数和尺度参数新的估计量,并通过比较偏差作为评价样本对估计参数下的分布效果.

关键词：伽马分布; 样本变异系数; 矩估计量

收稿日期：2015-01-12

基金项目：山东省自然科学基金项目(ZR2013FM012)

作者简介:陈超,男,chenchao881014@126.com

文章编号：1672-6197(2016)01-0033-04

中图分类号：O213

文献标志码：A

Abstract:The problem of parameter estimation with Gamma distribution occupied a very important position in the mathematic. In this paper, by means of moment estimation through the independence of sample coefficient of variation, we constructed the new estimators of shape parameter and scale parameter of Gamma distribution and estimated distribution parameters by comparing the deviation.

EstimatingparametersofGammadistribution

basedonsamplecoefficientofvariation

CHENChao,MENGZhao-wei

(SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China)

Keywords:Gammadistribution;samplecoefficientofvariation;momentestimator

参数估计作为Gamma分布研究的核心问题,是长期以来制约它们实际应用的主要技术瓶颈,倍受各国学者关注.Frery等人在提出Gamma分布的同时也指出该分布的参数估计存在困难[1].为了寻找一种较好的参数估计方法,多年来国内外学者进行了大量的探索和研究.早在1924年美国学者福斯特采用传统的矩法估计参数，但此后他认识到矩法估计误差太大.1946年,前苏联数学家克里茨基、闵凯里采用最小模比公式进行了参数估计.由于总体最小模比系数无法确定,导致结果出现了严重偏差. 1960年,前苏联学者阿列克谢夫推荐用三点法估计Gamma分布参数,三点法同样受到个别观测误差的巨大影响,缺乏平差功能.Hwang和Hu通过Gamma分布的随机样本证明了样本变异系数的独立性[2].本文将利用这一特性推导出样本变异系数平方的期望和方差,进而提出Gamma分布形状参数和尺度参数的新的矩估计量.

1参数估计的基本原理

Gamma分布参数的新的矩估计量,需要Hu和Hwang的如下定理[3].

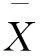
下面的结论以及定理1有助于求出Vn2的期望和方差.

定理2设X1,…,Xn为Gamma分布密度函数的随机变量,其Gamma密度为

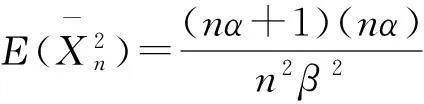
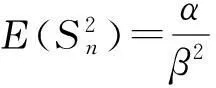
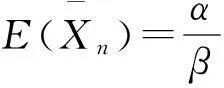
则

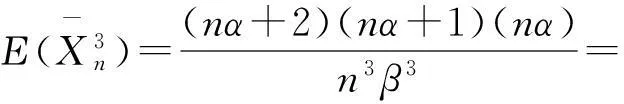
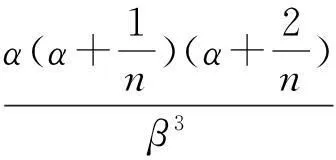
证明 很容易得到

(1)

由样本变异系数的定义[4]可知

且其k阶距为

(2)

由(1)和(2)得

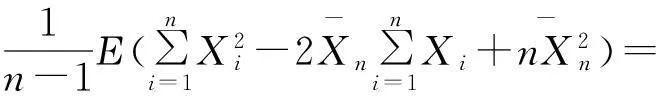
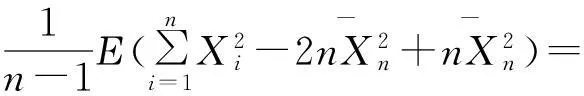
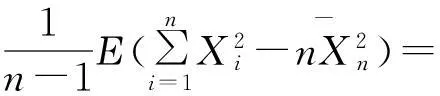
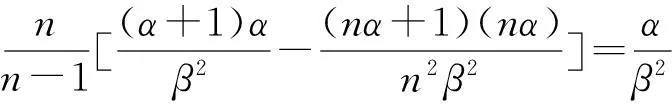
定理2证毕.

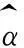
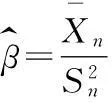
2Gamma分布参数的新的矩估计量

定理3 设X1,…,Xn为Gamma分布密度函数的独立同分布随机变量,其密度函数为

(x>0,α>0,β>0)

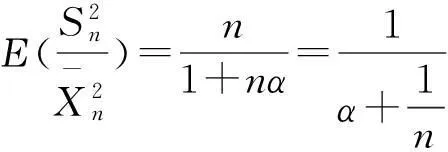
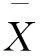
证明 由定理1,可以得到

由定理2,根据上述等式得

定理3证毕.

注意到:当n→时,.由于是样本变异系数的平方,因此是样本变异系数平方的渐近无偏估计量.

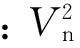
(3)

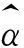
(4)

由Gamma分布的性质得:

则:

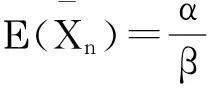
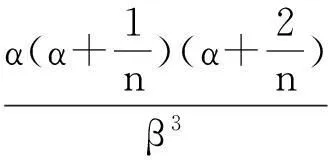
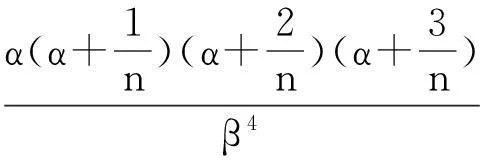
由上述等式得:

(5)

由定理2和等式(5)得:

即

由此可得

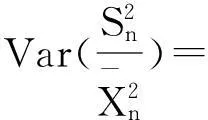
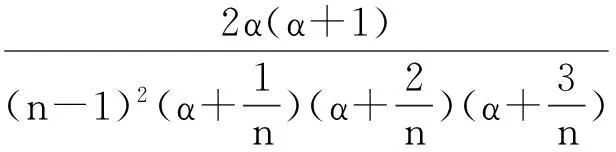
(6)

这样可以认为当样本足够大时,样本变异系数可以看做常数.它可以用作检验结果以及估计标准差.

3偏差

由偏差的定义[8]可知:

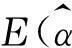
1)给定α和n得到Γ(α,n).

2)取100 000个独立的蒙特卡罗样本,每组样本容量为n.

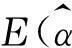
nα=0.1α=1.0α=4.0α=1550.1271.1216.6430.4100.1211.0855.9827.5200.1151.0785.0123.11000.1131.0314.2315.72000.1091.0134.1115.2

4估计量的比较

再次用蒙特卡罗法来比较在有限样本下Gamma分布的各种形状参数估计量的偏差,从而更好地认识各种参数估计量的优劣.不失一般性,把Gamma分布尺度参数β设为1.0.

表2Gamma分布不同参数估计量的偏差

nα^MOMα^MLEα^M50.0630.0310.027100.0510.0220.021200.0350.0090.0151000.0130.0020.0135000.0040.0010.009α=0.1β=1.0

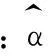
5结束语

本文利用样本变异系数的独立性提出了求解Gamma分布参数估计的新方法.首先通过样本矩估计总体矩得到了形状参数α和尺度参数β的估计量,然后利用样本变异系数的特性构造了该分布参数的新的估计量.并进行了一定的数据分析,利用这种方法可以将此类问题简单化.

参考文献

[1]HuCY.Onsignaltonoiseratiostatistics,Ph.D.ThesisInstituteofStatistics[J].NationalStatisticsUniversity,1990, 42: 248-354.

[2]HwangTY，LinYK.Onthedistributionofthesampleheterogeneityogmolecularpolymer,TamsuiOxfordJournalofMathematicalSciences[J].MathematicalStatisticsandAppliedProbability,2000,16(2), 133-149.

[3]JohnsonNJ，KotzS.ContinuousUnivariateDistributions[M].Wiley,NewYork,2007, 29:183-191.

[4]YoungDH,BakirST.Biascorrectionforageneralizedlog-gammaregressionmodel[J].Technometrics, 2011,29:183-191.

[5]BanardGA.Pivotalmodelsandthebayesiancontrovery[J].BulletinoftheInternationalStatisticalInstitute,1997, 47, 543-551.

[6]WeerahandiS.Exactstatisticalmethodsfordataanalysis[J].BiometricalJournal, 2006,48, 149-156.

[7]HoeffdingWA.Classofstatisticswithasymptoticallynormaldistributions[J].AnnMathStat.,1998,19:293-325.

[8]CaoShimin,N-foldconvolutionofgammadistributiondensityfunctionwhentheshapeparameterisapositiveinteger[J].MathematicalStatisticsandAppliedProbability, 1992, 7:22-27.

(编辑：刘宝江)