一个整系数多项式的整数解
2016-01-15曹永林1
肖 凌,曹永林1
(1. 山东理工大学 理学院, 山东 淄博 255049; 2.淄博理工学校 汽修系, 山东 淄博 255100)
一个整系数多项式的整数解
肖凌1,2,曹永林1
(1. 山东理工大学 理学院, 山东 淄博 255049; 2.淄博理工学校 汽修系, 山东 淄博 255100)
摘要:作为数论中一个熟知结论的推广,利用Gauss-Wilson定理和中国剩余定理,对任意正整数n,确定出了多项式+1模n的全部整数根,进而对任意整数x刻画出了其取值情况.
关键词:原根;中国剩余定理;整数的剩余表示
收稿日期:2015-01-09
通信作者:
作者简介:肖凌,女,autumndaisy@163.com;曹永林,男,ylcao@sdut.edu.cn
文章编号:1672-6197(2016)01-0026-03
中图分类号:O156.1
文献标志码:A
Abstract:As a generalization of a wellknown result in elementary number theory, we investigate the zeros of the polynomial
Thevalueandzerosofsomepolynomialwithintegercoefficients
XIAOLing1,2,CAOYong-lin1
(1.SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China;
2.AutoRepairDepartment,ZiboSchoolofTechnology,Zibo255100,China)

inthisnote.Furthermore,wegiveacompleteaccountofthevalueofitbyChineseRemainderTheoremandGauss-WilsonTheorem.
Keywords:primitiveroot;chineseremaindertheorem;modularrepresentationofintegers

定理1[1]设p为给定的素数,则对任意整数x恒有同余式

1预备知识

或
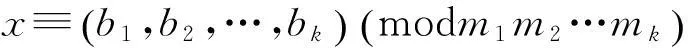
引理1设m,n是互素的两个正整数,则有

推论1 设m,n是互素的正整数,则有


2主要结果及其证明


1)如果x与pα互素,则必存在ri,1i使得且根据欧拉定理知,此时从而

2)如果x与pα不互素,则对于模pα缩系中任意ri有

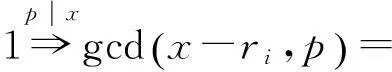



(1)


(2)
由式(1), (2)知




(2)n=2α0,α0>2;

其中pi为奇素数,αi>0,i=1,…,k,为了叙述方便,令p0=2.我们有
定理3设正整数n不具有原根,沿用上面的记号,对任意整数x,令

则有如下剩余表示





由推论1知


(3)







综合上述结论,容易得到:



例当n=100=22×52时,令m1=22,m2=52,有
M1=25,M1′=1;M2=4,M2′=19.



参考文献
[1]柯召,孙琦. 数论讲义:上册[M]. 2版,北京: 高等教育出版社,2010.
[2]AyahA,MelanieMW,Countingpolynomialsoverfinitefieldswithgivenrootmultiplicities[J].JournalofNumberTheory, 2014, 136: 392-402.
[3]DineshST.FermatversusWilsoncongruences,arithmeticderivativesandzetavalues[J].JournalofNumberTheory, 2015, 32: 192-206.
[4]HardyGH,WrightEM.Anintroductiontothetheoryofnumbers[M]. 6thed. 北京: 人民邮电出版社,2009.
[5]DicksonLE.Historyofthetheoryofnumbers:Volume1[M].NewYork:ChelseaPublishingCompany, 1952.
(编辑:姚佳良)
