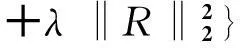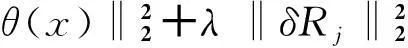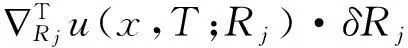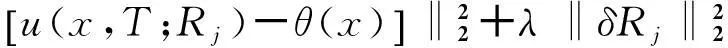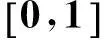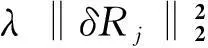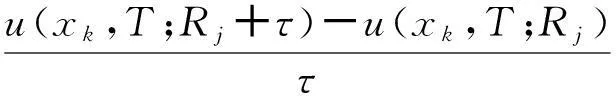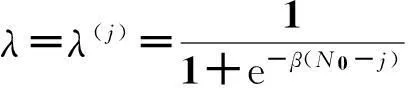时间-空间双边分数阶扩散方程微分阶数的反演

杜殿虎， 李功胜， 贾现正， 孙春龙

(山东理工大学 理学院， 山东 淄博 255049)

时间-空间双边分数阶扩散方程微分阶数的反演

杜殿虎， 李功胜， 贾现正， 孙春龙

(山东理工大学 理学院， 山东 淄博 255049)

摘要：研究了一维时间-空间双边分数阶扩散方程的求解与微分阶数的数值反演问题.基于Caputo意义下时间分数阶导数和Grünward-Letnikov意义下空间双边分数阶导数的离散,给出了一个有限差分求解格式,证明了其稳定性和收敛性.分别基于终值数据及区域中点处的观测值作为附加数据,应用同伦正则化算法对微分阶数进行数值反演.反演结果表明同伦正则化算法对于分数阶扩散方程的微分阶数反演是有效的.

关键词：分数阶扩散方程； 反问题； 差分格式； 稳定性与收敛性； 同伦正则化； 数值反演

收稿日期：2015-01-29

基金项目：国家自然科学基金项目(11371231, 11071148)； 山东省自然科学基金项目(ZR2011AQ014)

通信作者：

作者简介：杜殿虎,男,dudianhu@126.com；李功胜，男，lgs9901@163.com

文章编号：1672-6197(2016)01-0021-05

中图分类号：O175

文献标志码：A

Abstract:This paper deals with numerical solution to the time-space Caputo-Riesz fractional diffusion equation and inversion for the fractional orders. A finite difference scheme is introduced to solve the forward problem based on Caputo’s discretization to the time fractional derivative and Grünward-Letnikov’s discretization to the space fractional derivatives, and unconditional stability and convergence for the difference scheme are proved by fine estimation to the spectral radius of the coefficient matrix of the scheme. Furthermore, numerical inversions for determining the fractional orders are carried out with random noisy data at the final time and the inner point using the homotopy regularization algorithm. The numerical solutions give good approximations to the exact solution demonstrating the effectiveness of the proposed algorithm

Numerical determination of the fractional orders for

time-space two-sided fractional diffusion equation

DU Dian-hu, LI Gong-sheng, JIA Xian-zheng, SUN Chun-long

(School of Science, Shandong University of Technology, Zibo 255049, China)

Key words: fractional diffusion equation; inverse problem; finite difference scheme; stability and convergence; homotopy regularization algorithm; numerical inversion

随着近年来应用学科的发展,对于分数阶反常扩散模型的研究逐渐成为现代各门科学与数学相互驱动发展的一个主要方面.已有研究表明,与传统的整数阶微分方程比较,分数阶微分方程能够更好地拟合某些自然物理过程和动态系统过程,因此其在工程、物理、地下水、金融和环境问题中得到了广泛的应用[1-4].不过从数学理论及其方法研究的角度,分数阶微分方程还有许多问题值得深入研究.

对于分数阶扩散的相关反问题研究,程晋等[5]人首先研究了时间分数阶反常扩散方程在齐次Neumann边界及δ函数为初始条件下,基于边界测量数据确定分数阶数和扩散系数的联合反演问题,并证明了反问题解的唯一性；随后李功胜等[6]继续研究了一般连续初值条件下对于时间微分阶数与扩散系数联合反演的唯一性,并给出了数值反演模拟.最近,东京大学的山本昌弘教授等[7]考察了含多个时间阶导数的扩散方程中多个微分阶数的反问题，也给出了反问题解的唯一性证明；李新洁等[8]研究了非对称双边空间分数阶扩散方程的全离散差分格式求解,并应用最佳摄动量算法对微分阶数与扩散系数进行了联合反演模拟；贾现正等[9]探讨了时间-空间左侧分数阶变系数对流扩散方程差分求解与微分阶数的数值反演问题,通过对系数矩阵谱半径的精细估计,证明了差分格式的无条件稳定性和收敛性,同时应用同伦正则化算法对时间-空间微分阶数进行了有效的数值反演.

本文将探讨时间-空间双边分数阶扩散方程微分阶数的反演问题.对于这类同时含有时间分数阶和空间双侧分数阶导数的扩散方程正问题的数值求解,已有不少研究[10-14].主要是差分方法,且其差分格式收敛性与稳定性的证明是基于逐行估计的方法.本文继续研究该正问题的差分求解,不过文中将采用一种新的证明方法,即通过对系数矩阵主对角元素的精细估计,获得系数矩阵的谱半径估计,进而直接证明差分格式的无条件稳定性和收敛性.这种方法相比已有方法显得简洁清晰.进一步,本文还将探讨利用终值数据和内点观测数据确定时间、空间微分阶数的反问题.应用同伦正则化算法,分别进行精确数据和扰动数据条件下的数值反演模拟,反演解与真解吻合较好.结果表明对于所研究的时间-空间双边分数阶扩散模型,同伦正则化算法可以有效实现对微分阶数的数值确定.

1正问题及其数值求解

对于l>0,T>0,考虑时间-空间双边分数阶扩散方程的初边值问题：

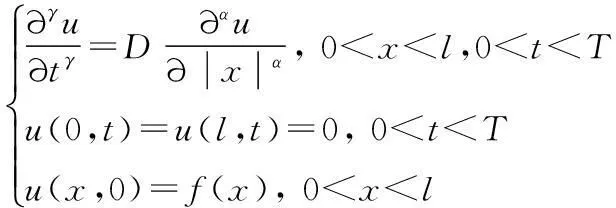
(1)

其中0<γ<1为时间分数阶导数,1<α<2为空间分数阶导数,D>0为扩散系数,f(x)∈C([0,l])为初值函数.这里的时间分数阶导数取Caputo的定义：

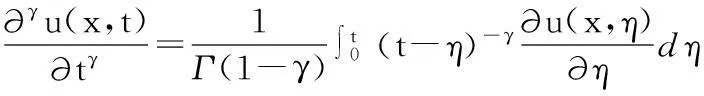
(2)

空间双边分数阶导数定义为：

(3)

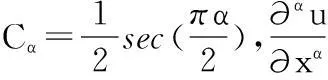
(4)

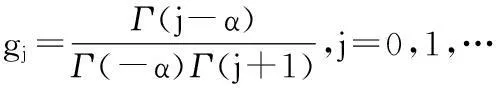
下面先给出求解正问题(1)的一个隐式差分格式.

1.1　正问题求解的差分格式

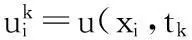
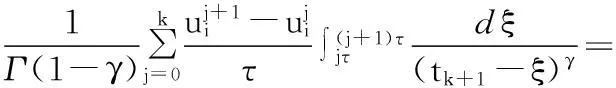
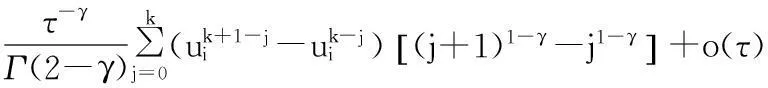
(5)

其次,根据式(4)并利用移位的Grünward近似公式,空间双边分数阶导数离散为:

(6)

于是,略去高阶项,原方程被离散为：

(7)

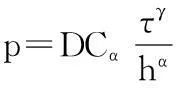
当k=0时,

(8)

当k>0时,

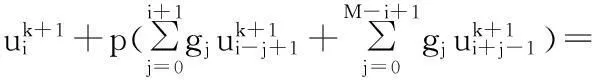
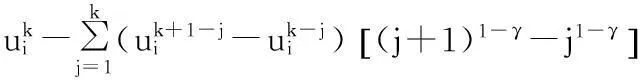
(i=1,2…,M-1)

(9)

用矩阵形式表示,即有：

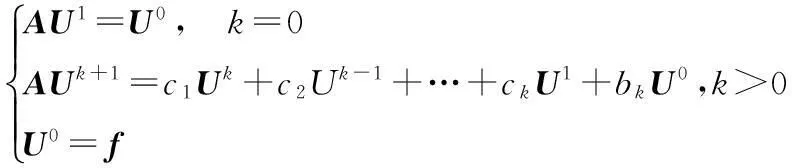
(10)

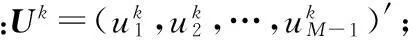
f=(f(x1),f(x2),…,f(xM-1))′;

cj=2j1-γ-(j+1)1-γ-(j-1)1-γ,

j=1,2,…,k;bk=(k+1)1-γ-k1-γ,

k=1,2,…,N-1;

A=(ai,j),i,j=1,2…

M-1,aij定义为:

(11)

1.2　稳定性和收敛性

本小节给出差分格式(10)的稳定性和收敛性.

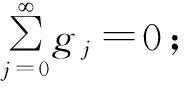
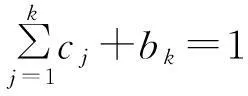
引理3对于矩阵A∈R(M-1)×(M-1)以及任意的ε>0,至少存在一种矩阵范数‖·‖*使得:

‖A‖*≤ρ(A)+ε.

注意到由式(10)给出的矩阵A的结构,利用引理1,可得如下命题:

由命题1可知,以A为系数矩阵的差分格式有唯一解.进一步可得系数矩阵的谱半径估计.

定理1对于式(10)定义的系数矩阵A,记‖a‖,

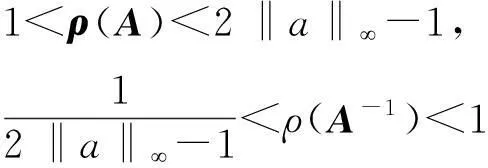
(12)

利用差分格式线性性,容易得到：

(13)

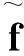
定理2隐式差分格式(10)无条件稳定.

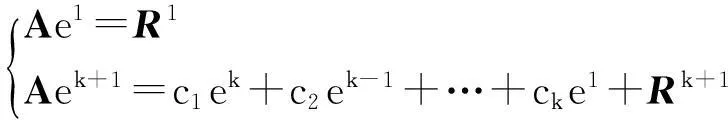
(14)

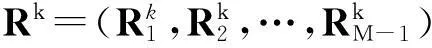
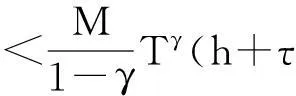
1.3　数值试验

运用分离变量法及Laplace变换,可得正问题(1)的解析解表达式:

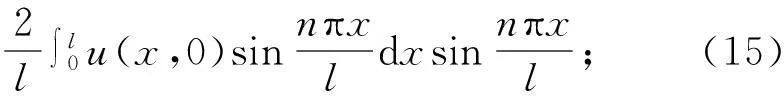
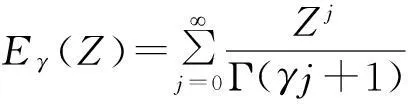
u(x,t)=

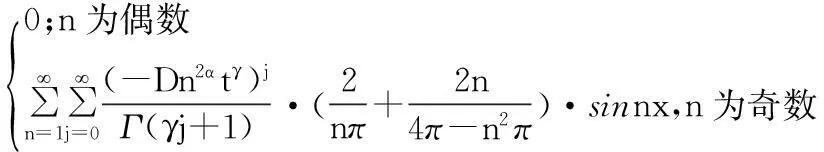
分别利用上述解析解表达式与差分格式(10)进行正问题的计算,数值结果绘于图1.

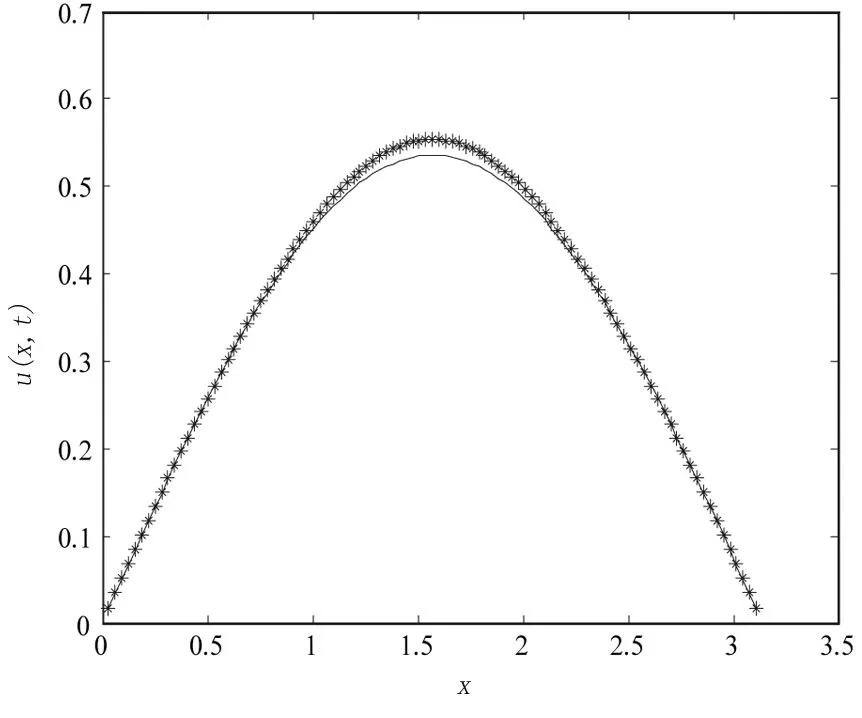
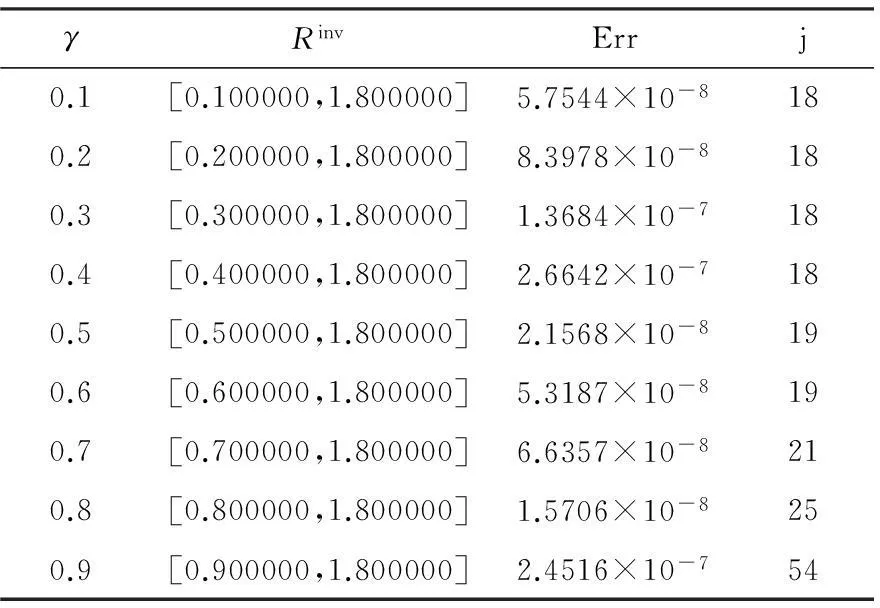
图1 　α=1.9,γ=0.9,t=0.5时解析解与数值解的比较,-:解析解,*:数值解

从图1看出，除了在区域中点处解误差稍大以外,数值解与解析解都吻合得较好,说明了差分格式的有效性.

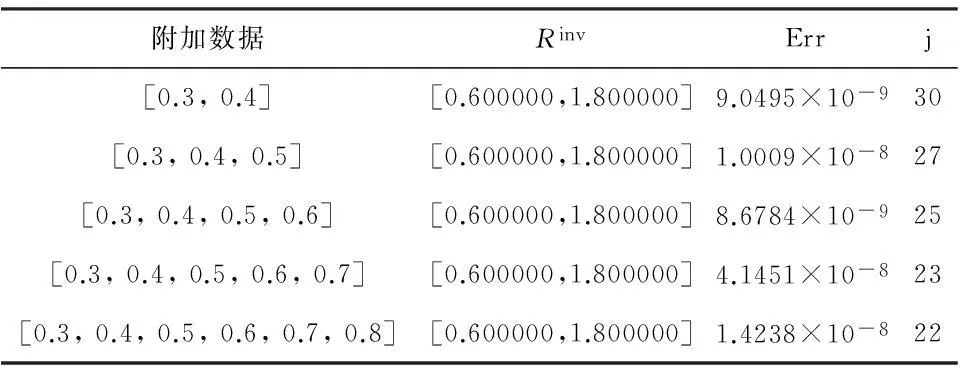
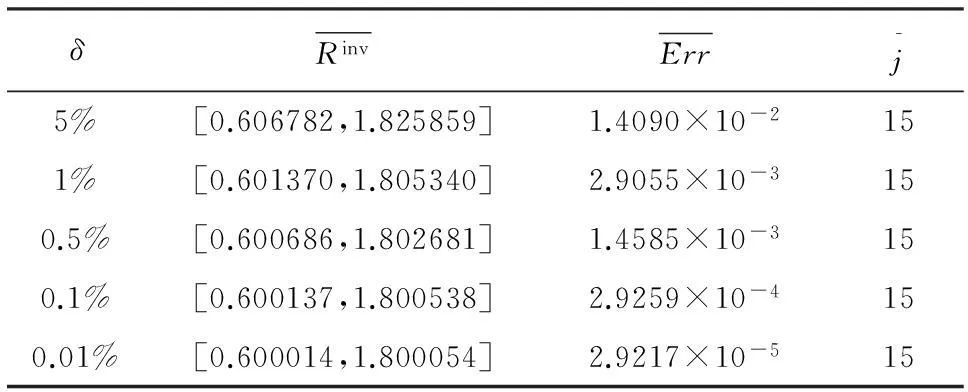
2反问题与反演算法

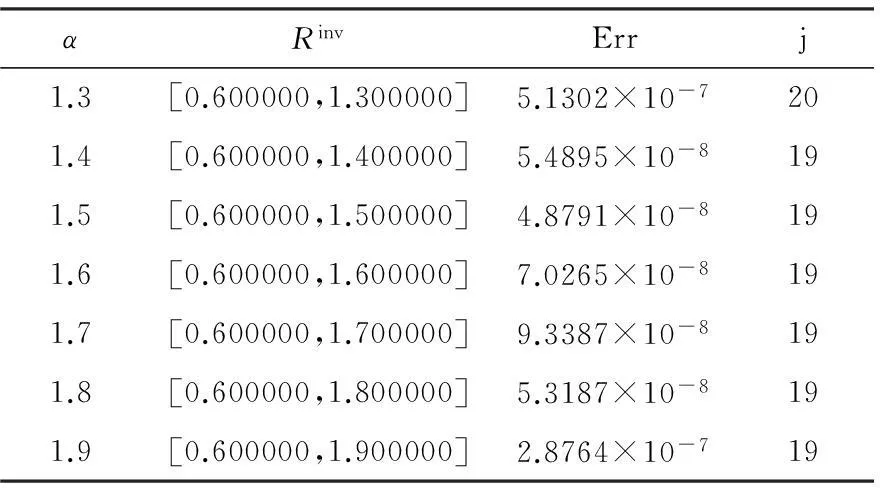
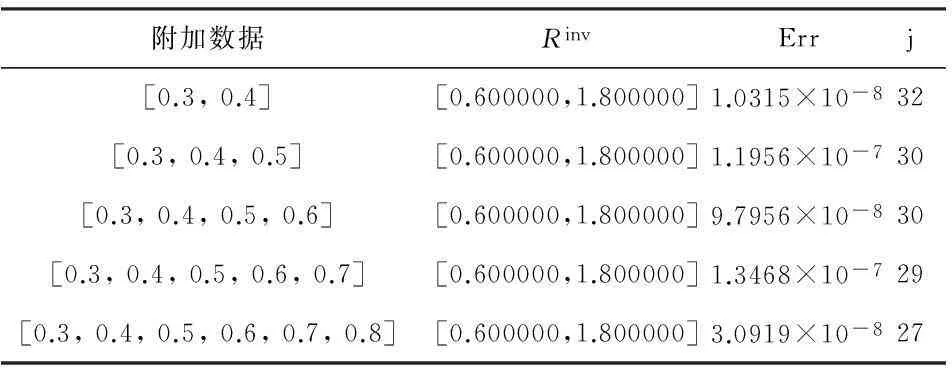
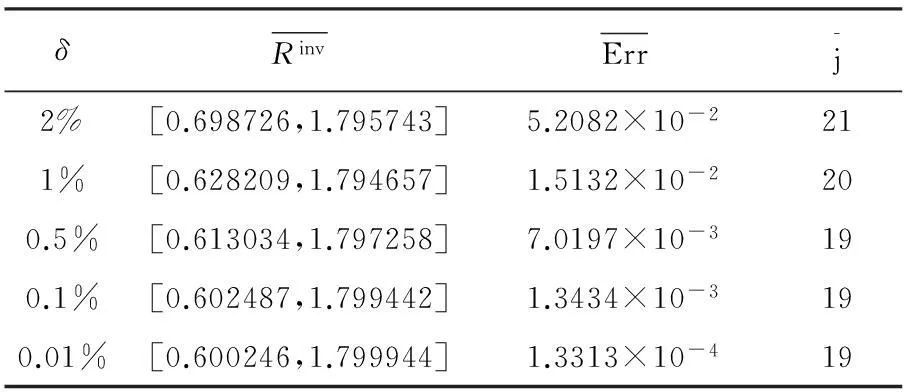
当微分阶数α与γ未知时,给定时刻t=T的观测值

u(x,T)=θ(x),0

(16)

则由式(1)联合式(16)构成了确定微分阶数α与γ的一个反问题.另外,如果给定区域内某一点x=x0处的时间观测值作为附加数据,即有附加条件:

u(x0,t)=θ(t),0≤t≤T

(17)

则由(1)联合(17)也形成一个确定微分阶数的反问题.

本文对γ,α的数值反演采用同伦正则化算法[15-17].记I=(0,1)×(1,2),设R=(γ,α)∈I,则上述问题可以转化为如下极小泛函的求解:

(18)

其中λ>0是同伦(正则)参数.根据最佳摄动量算法思想,上述极小泛函问题可以转换成对于给定的初始迭代值R0求解最佳摄动量δRj,即设

Rj+1=Rj+δRj,j=0,1,2,…

(19)

δRj是下述泛函的极小解:

F(δRj)=(1-λ)‖u(x,T;Rj+δRj)-

(20)

将u(x,T;Rj+δRj)在Rj处作Taylor展开,略去高阶项得到:

u(x,T;Rj+δRj)≈u(x,T;Rj)+

则上述误差函数可表示为:

F(δRj)=(1-λ)‖Tu(x,T;Rj)·δRj+

(21)

(22)

其中:

B=(bks)K×S,bks=

ξ=(u(x1,T;Rj),u(x2,T;Rj)，…，u(xk,T;Rj)),η=(θ(x1),θ(x2),…,θ(xK))

τ是数值微分步长.上述泛函极小值问题相当于求解规范方程:

((1-λ)BTB+λI)δRj=(1-λ)BT(η-ξ)

(23)

实际反演计算中，同伦参数取为拟神经网络函数,即有：

(24)

其中N0,β为可调参数,j为迭代步数,λ(j)为第j个迭代步时同伦参数的取值.上述算法实施步骤为：

步骤1给定初始迭代值R0和数值微分步长τ,求向量η,ξ及矩阵B;

步骤2按照同伦算法进行计算,由式(23)求出δRj;

步骤3对于给定的精度eps,判断是否满足‖δRj‖≤eps;若是则Rj即为所求,算法终止;否则由式(20)得到Rj+1,转到步骤1继续进行.

3数值反演

以下算法实现中,若没有特别说明,正问题计算中取l=π,T=1,D=0.5,M=N=100,反演参数分别取为τ=0.01,eps=le-5,N0=5，β=0.5.

算例1 (基于终值数据的反演)设f(x)=sinx,取微分阶数真解Rtrue=[0.6,1.8],初始迭代K0=[0.2,1.4].首先考察微分阶数对反演的影响,反演结果列于表1与2,其中γ,α分别表示时间与空间微分阶数,Rinv表示反演解,j为迭代次数,Err表示反演解与真解的相对误差.

表1时间微分阶数对反演的影响

γRinvErrj0.1[0.100000,1.800000]5.7544×10-8180.2[0.200000,1.800000]8.3978×10-8180.3[0.300000,1.800000]1.3684×10-7180.4[0.400000,1.800000]2.6642×10-7180.5[0.500000,1.800000]2.1568×10-8190.6[0.600000,1.800000]5.3187×10-8190.7[0.700000,1.800000]6.6357×10-8210.8[0.800000,1.800000]1.5706×10-8250.9[0.900000,1.800000]2.4516×10-754

表2空间微分阶数对反演的影响

αRinvErrj1.3[0.600000,1.300000]5.1302×10-7201.4[0.600000,1.400000]5.4895×10-8191.5[0.600000,1.500000]4.8791×10-8191.6[0.600000,1.600000]7.0265×10-8191.7[0.600000,1.700000]9.3387×10-8191.8[0.600000,1.800000]5.3187×10-8191.9[0.600000,1.900000]2.8764×10-719

由表1,2得出,时间分数阶对反演算法的实施具有一定的影响,随着时间微分阶数的变大,迭代步数慢慢增加,而空间分数阶对反演的影响不大.

进一步考察附加数据选取的多少对反演算法的影响,计算结果列于表3.

表3附加数据选取对反演的影响

附加数据RinvErrj[0.3,0.4][0.600000,1.800000]1.0315×10-832[0.3,0.4,0.5][0.600000,1.800000]1.1956×10-730[0.3,0.4,0.5,0.6][0.600000,1.800000]9.7956×10-830[0.3,0.4,0.5,0.6,0.7][0.600000,1.800000]1.3468×10-729[0.3,0.4,0.5,0.6,0.7,0.8][0.600000,1.800000]3.0919×10-827

由表3看出,附加数据选取的多少对反演精度影响不大,只是附加数据选取较多时迭代步数稍微减少.最后,考察附加数据的扰动对反演结果的影响.由于随机扰动的影响,每次的反演计算解并不一样.表4列出了连续10次反演计算的平均值.

由表4得出,数据扰动对反演结果影响较大.不过，随着数据扰动水平的减小,反演精度逐步提高,这反映了反演算法的数值稳定性.

表4附加数据的随机扰动对反演的影响

δRinvErrj　2%[0.698726,1.795743]5.2082×10-2211%[0.628209,1.794657]1.5132×10-2200.5%[0.613034,1.797258]7.0197×10-3190.1%[0.602487,1.799442]1.3434×10-3190.01%[0.600246,1.799944]1.3313×10-419

算例2(基于区域中点处观测数据的反演)设f(x)=sin2x,微分阶数真解与初始迭代与算例1一样.本例仅考察附加数据的多少以及数据扰动对反演的影响,计算结果列于表5与6.

表5附加数据选取对反演的影响

附加数据RinvErrj[0.3,0.4][0.600000,1.800000]9.0495×10-930[0.3,0.4,0.5][0.600000,1.800000]1.0009×10-827[0.3,0.4,0.5,0.6][0.600000,1.800000]8.6784×10-925[0.3,0.4,0.5,0.6,0.7][0.600000,1.800000]4.1451×10-823[0.3,0.4,0.5,0.6,0.7,0.8][0.600000,1.800000]1.4238×10-822

表6附加数据的扰动对反演的影响

δRinvErrj　5%[0.606782,1.825859]1.4090×10-2151%[0.601370,1.805340]2.9055×10-3150.5%[0.600686,1.802681]1.4585×10-3150.1%[0.600137,1.800538]2.9259×10-4150.01%[0.600014,1.800054]2.9217×10-515

由表5、6可以看出,与算例1一样,附加数据选取的多少对反演精度影响也不大,较多的附加数据所需的迭代步数较少;不过,本例中数据的随机扰动对反演算法的影响比算例1要小,反映出算例1的病态性较大.

4结束语

本文探讨了时间-空间双边分数阶扩散方程微分阶数的反演问题.文中建立了正问题求解的一种隐式差分格式,并给出了差分格式的稳定性和收敛性;进一步对于时间、空间两个微分阶数的反演问题,应用一种同伦正则化算法给出了精确数据与随机扰动数据情形下的数值反演.计算结果表明应用适当的反演算法可以有效实现对于复杂的分数阶扩散方程相关系数反问题的数值反演.

参考文献

[1]PodlubnyI.Fractionaldifferentialequations[M].SanDiego:Academic, 1999.

[2]KilbasAA,SrivastavaHM,TrujilloJJ.Theoryandapplicationsoffractionaldifferentialequations[M].Amsterdam:Elsevier, 2006.

[3]陈文，孙洪广，李西成,等.力学与工程问题的分数阶导数建模[M].科学出版社, 2010.

[4]郭柏灵，蒲学科，黄凤辉.分数阶偏微分方程及其数值解[M].北京：科学出版社, 2011.

[5]ChengJ,NakagawaJ,YamamotoM，et al，Uniquenessinaninverseproblemforaone-dimensionalfractionaldiffusionequation[J].InverseProblems, 2009, 25: 115002.

[6]LiGS,ZhangDL,JiaXZ, et al.Simultaneousinversionforthespace-dependentdiffusioncoefficientandthefractionalorderinthetime-fractionaldiffusionequation[J].InverseProblems, 2013, 29: 065014.

[7]LiZY,YamamotoM.Uniquenessforinverseproblemsofdeterminingordersofmulti-termtime-fractionalderivativesofdiffusionequation[J].ApplicableAnalysis,2015,94(3):570-579.

[8]李新洁，李功胜，贾现正.非对称分数阶对流弥散的数值模拟及参数反演[J]. 高等学校计算数学学报, 2013, 35(4): 309-326.

[9]贾现正，张大利，李功胜,等.空间-时间分数阶变系数对流扩散方程微分阶数的数值反演[J].计算数学, 2014, 36(2): 113-132.

[10]LiuF,ZhuangP,AnhV,et al.Stabilityandconvergenceofthedifferencemethodsforthespace-timefractionaladvection-diffusionequation[J].AppliedMathematicsandComputation, 2007, 191: 12-20.

[11]覃平阳,张晓丹,空间-时间分数阶对流扩散方程的数值解法[J].计算数学, 2008, 30: 305-310.

[12]苏丽娟,王文洽,双边空间分数阶对流扩散方程的一种有限差分解法[J]. 山东大学学报：理学版，2009, 44(10): 26-29.

[13]ShenSJ,LiuFW,AnhV.Numericalapproximationsandsolutiontechniquesforthespace-timeRiesz-Caputofractionaladvection-diffusionequation[J].NumericalAlgorithms, 2011, 56: 383-403.

[14]ChenZQ,MeerschaertMM,NaneE.Space-timefractionaldiffusiononboundeddomains[J].JournalofMathematicalAnalysisandApplications, 2012, 393: 479-488.

[15]苏超伟.偏微分方程逆问题的数值解法及应用[M]. 西安:西北工业出版社, 1995.

[16]LiGS,ChengJ,YaoD, et al.One-dimensionalequilibriummodelandsourceparameterdeterminationforsoil-columnexperiment[J].AppliedMathematicsandComputation, 2007, 190: 1365-1374.

[17]李功胜，姚德.扩散模型的源项反演及其应用[M].北京:科学出版社, 2014.

(编辑：姚佳良)