内孤立波波致流场数值模拟研究*

王 伟 郭海燕① 王 飞 苗得胜 马 东

(1. 中国海洋大学工程学院 青岛 266100; 2. 山东科技大学土木工程与建筑学院 青岛 266590)

随着南海资源开发的不断深入, 其复杂的海洋环境因素越来越受到专家学者的重视。南海内孤立波发生频繁, 对水下结构的正常工作产生严重影响, 给南海油气资源开发带来了极大挑战, 是南海海洋工程结构建设中不可忽略的环境荷载之一。

内孤立波发生在密度稳定分层的海洋内部, 其振幅远大于表面波(杜涛等, 2001), 主要通过非线性效应与色散效应达到一定程度的平衡实现稳定传播(Osborne et al, 1980), 目前应用比较广泛的内孤立波理论模型主要有 KdV、mKdV理论等(Choi et al,1999;Helfrich et al, 2006)。近几年, 内孤立波的研究方法有现场观测、理论研究、物理实验、数值模拟等。Liu等(2014)利用在中国南海获得的内孤立波SAR影像, 探索了海底地形以及水深变化对内孤立波传播速度的影响。2005年5月Xu等(2010)在南海西北陆架监测到高非线性的内孤立波, 通过将内孤立波数据与KdV、mKdV理论进行对比, 发现对于高非线性内孤立波, eKdV理论吻合效果更好。柯自明等(2009)在南海文昌内波实验中, 通过单点锚系测量观测到典型内孤立波, 并分析内孤立波波形、温度结构及波致斜压流。Michallet等(1998)通过将波形、相速度、振幅的理论模型计算结果与实验结果对比, 提出在振幅较小时 KdV理论与实验结果吻合较好, 而振幅较大时KdV-mKdV理论与实验结果较接近; Buick等(2003)通过实验室造波, 采用PIV技术监测内波流场,验证了理论计算结果与实验结果。近几年, 利用数值水槽进行模拟的计算流体力学(CFD)方法迅速发展起来。Zhang等(2012)使用CFD方法建立三维数值波浪水槽, 所得结果与 KdV理论计算结果较吻合, 证明该方法可有效模拟非线性内孤立波。陈钰等(2009)利用Fluent软件, 通过设置造波边界法, 成功建立了可有效模拟弱非线性内孤立波的分层流数值水槽; 高原雪等(2012)基于 MCC理论, 利用速度入口数值造波方法, 建立内孤立波数值水槽, 并实现了振幅可控的内孤立波数值模拟。目前国内外主要将 CFD数值模拟结果与理论结果进行对比分析, 而结合物理实验结果对比分析的研究较少。

本文采用CFD数值模拟方法, 基于Fluent软件,通过“平板拍击”方法, 建立具有多种设计振幅的内孤立波二维数值水槽。通过VOF方法(董志等, 2009)追踪两层流体界面变化, 利用软件自带的监视器功能观测不同高度处的波致水平流速, 并与物理实验结果进行对比, 验证数值模拟的有效性。利用数值造波结果, 研究内孤立波波致流场特性, 分析不同水深处的水平流速, 以及波谷经过断面时波致水平流速垂向分布。

1 建立数值水槽

采用两层流体模型, 使用Navier-Stokes方程作为流场的控制方程。建立内孤立波二维数值水槽。数值水槽尺寸如下: 长 1500cm, 高 58cm, 其中上层流体高度9.5cm, 下层流体高度48.5cm。利用直角坐标系对水槽进行定位, x轴与两层流体的交界面重合, 正方向沿水槽长度方向向右; y轴与水槽左边界重合, 且正方向沿水槽高度垂直向上。数值水槽模型如图1所示, 其中造波板长度为80cm, 挡板长度为15cm。

图1 数值水槽示意图Fig.1 The sketch of numerical wave tank

其边界条件设置为: 造波板设置为移动边界, 挡板、水槽的下边界及左、右边界设为壁面边界(wall)。根据刚盖近似原理(方欣华等, 2005), 内孤立波在两层流体的自由表面上引起的波动较小, 故将水槽的上表面设为壁面边界(wall)。

“平板拍击”造波方法原理为: 选取合适的内波理论, 通过 UDF用户自定义函数来控制造波板的运动速度, 使造波板作上下运动, 并利用动网格技术,在两层流体界面产生内孤立波。使用 Navier-Stokes方程作为流场的控制方程, 在两层流体模式下, 描述内孤立波运动的方程主要有KdV、mKdV等。设上下层流体水深、密度分别为:1h、1ρ和2h、2ρ, (,)x tη为波面方程。KdV理论下方程解的形式(Michallet et al, 1998)如下:

式中:

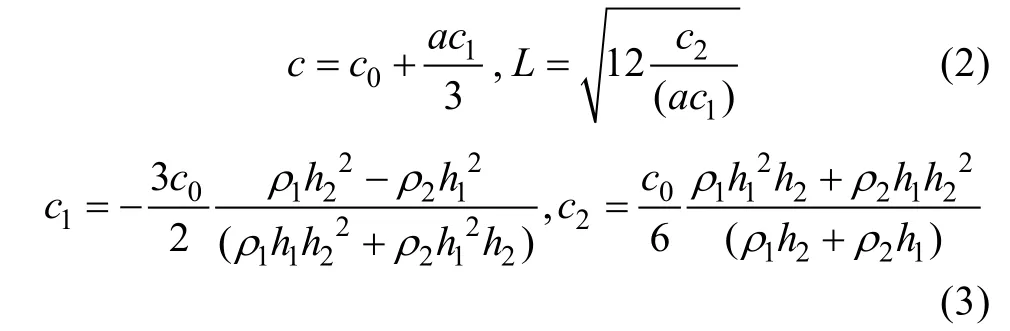
mKdV理论下方程解的形式(Michallet et al,1998)为:

式中:

a为内孤立波振幅, 负号表示内孤立波波面是向下凹的。L表示内孤立波的特征波长。根据KdV、mKdV理论对不同振幅水深比(a/H)的使用条件, 可分别选用 KdV或 mKdV理论编写控制造波板运动速度的UDF程序。其中造波板的运动速度 v(t)可定义为(徐鑫哲, 2012):D为造波板的长度, c为内孤立波的相速度。其数学原理为: 造波板上下运动过程中, 根据体积守恒, 单位时间内造波板排开的流体体积与造波板右端两层流体交界面沿 x轴前进的体积相等, 即:

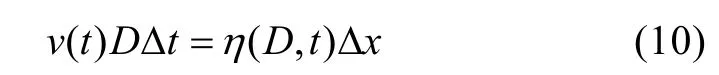
其中, Δx = cΔ t 。因此:

数值水槽的网格划分: 采用结构化网格对水槽进行网格离散。为了方便、准确的捕捉内孤立波波面, 在内孤立波形成的高度范围内, 即两层流体的交界面附近, 对网格划分进行加密处理。其中在垂直方向y= –8.5cm至y=0.5cm范围内, 划分的网格大小为 0.5cm, 而为了提高计算效率, 在加密区两侧的高度范围内, 分别从加密区开始, 向两侧方向采用渐变网格划分方法, 网格尺寸的渐变比例为1.02。由于水平方向即x向的网格划分对内孤立波波面的形成影响较小, 故沿x向的网格划分可以取为2cm一个网格。数值水槽的网格划分情况如下图所示:

图2 数值水槽网格划分示意图Fig.2 The gridding of the numerical flume

求解设置: 将建立好的数值水槽模型导入Fluent中进行求解设置, 设置上层流体密度1ρ=1035kg/m3,下层流体密度2ρ=1054kg/m3。选取Fluent自带的kε-湍流模型, 采用VOF方法追踪两层流体的交界面, 对控制方程的离散使用有限体积法, 压力速度耦合方法选用 PISO算法, 对流相及输运方程的离散采用一阶迎风格式。

由于数值水槽的右边界为固壁边界, 内孤立波传播到该位置处时易产生反射波, 为避免反射波对流场产生干扰, 采用阻尼消波(孙大鹏等, 2000; 韩朋等, 2009)的方法在水槽末端进行消波处理: 取水槽末端 1—2倍波长处作为消波段, 通过在消波段动量方程中添加阻尼源项使波浪传播到该消波段时能量逐渐被吸收。

按照振幅大小分为四个工况, 将四个工况下的内孤立波振幅分别作为数值水槽的设置波高, 进行数值造波模拟计算:

表1 数值模拟工况设置Tab.1 Setting of amplitude for the numerical simulation

根据 KdV、mKdV理论对不同振幅水深比(a/H)的使用条件, 由于工况1、2中a/H＜0.1, 故选用KdV理论定义造波板的速度; 而工况三、四中a/H＞0.1, 故选用mKdV理论定义造波板的速度(黄文昊等, 2013)。

迭代计算: 各项参数设置完成后进行流场的迭代计算, 设置迭代时间步长为 0.01s, 每个时间步的最大迭代计算次数为20次。

2 数值模拟结果分析

2.1 内波物理实验方法

开展内波物理实验检验数值模拟结果, 该实验在中国海洋大学物理海洋实验室分层流水槽中进行,造波方法采用重力塌陷法。水槽尺寸为: 15m×0.35m×0.7m(长、宽和高), 额定水深为0.6m。密度分层采用Oster双缸法制取, 上层流体高h1=9.5cm, 密度ρ1=1035kg/m3; 下层流体高度h2=48.5cm, 密度ρ2=1054kg/m3。图3为物理造波示意图。

使用PIV(Wangetal, 2015)技术, 将体积很小、密度与流体相当、反光性能良好的镀银空心微珠粒子按一定浓度布置于液体中, 粒子能随流体运动, 代表流体质点的运动。待内波稳定传播后, 在水槽中部采用CCD系统对粒子的位置进行拍摄, 采样频率为50Hz,每张图像分辨率为1920×1080像素。运用图像处理软件进行分析, 可以得到断面处粒子的运动状态, 即该处的流场状态。

图3 造波示意图Fig.3 Experimental wave generation

2.2 数值造波结果验证

首先分析内孤立波数值模拟得到的波形, 并与实验结果进行对比, 以验证本次数值造波的合理性:

图5为数值造波得到的波形数据, 并分别与内孤立波物理实验结果进行对比。由图中可以看出, 工况一、二的数值造波结果与实验结果吻合较好, 只是在波形尾端数值造波结果存在较小的波动, 这是内孤立波在生成过程中会产生尾波所致, 但在内波传播过程中会逐渐衰减, 并不会对内波产生影响。工况三的数值造波结果在波形方面与实验一致, 且尾波较小。工况四的数值造波结果在波形的后半段与实验一致, 在波形前半段数值造波结果优于实验结果, 因此工况四的造波结果也是合理的。

综上, 本文建立的数值水槽能够实现设计振幅的内孤立波数值造波, 且数值结果与实验结果较吻合, 能有效实现对内孤立波的数值模拟。

图4 数值造波波形与实验对比Fig.4 Comparison in shape of the waves generated between numerical simulation (red lines) and experiment (black lines) in different amplitudes

3 讨论

3.1 上下层流体中波致水平流速分布

在数值造波过程中, 针对四个工况, 分别设置监视器观测上下层流体中间位置处波致水平流速的变化。观测位置高度: (1)y=5cm, 即上层流体中间位置处; (2)y= –24cm, 即下层流体中间位置处。观测结果如下图所示, 并与实验结果进行对比:

图5 内孤立波波致水平流速变化Fig.5 Comparison in horizontal velocity magnitude induced by generated internal solitary waves between numerical simulation(red lines) and experiment (black lines) at different depth

图6为内孤立波波致水平流速变化图, 并与实验结果进行对比, 经过对比发现, 工况一、二中, 波致水平流速的数值模拟结果的变化与实验一致; 工况三、四中, 在下层流体中, 数值模拟结果的变化与实验一致, 而在上层流体中差异较大。原因为: 在工况三和工况四的实验中, 上层流体的流速值较大, 超出流场测量系统的测量范围, 造成监测数据失真。但是从工况一、二的对比以及工况三、四下层流体中流速的对比可得出结论: 数值模拟结果与实验结果吻合较好。

由图6可看出, 随时间的推移, 内孤立波波致水平流速在上下层流体中的方向相反, 上层流体中的速度与波形传播的方向一致, 下层流体中的速度与波形传播方向相反; 上下层流体中的水平速度均呈现先增大后减小的趋势; 在波谷经过的时刻, 上下层流体中的水平速度均达到最大, 且上层流体的速度最大值大于下层流体。

表2为四个工况下, 由数值造波得到的上下层流体中间位置处内孤立波波致水平流速的最大值。由表2而得出结论: 随振幅的增加, 波致水平流速逐渐增大。

表2 内孤立波波致水平流速的最大值Tab.2 The maximum horizontal velocity induced by internal solitary waves

3.2 波致水平流速沿垂向分布

图 7为各工况下波谷经过断面处波致水平流速沿垂向的分布, 并与实验结果进行对比。其中工况一、二、三中, 数值模拟结果与实验结果一致; 在工况四中, 由于上层流体中波致水平流速较大, 致使实验监测失效, 因此实验结果失真。

从图中可以看出: (1)内孤立波波致水平流速在上下层流体中的方向相反; (2)内孤立波波致水平流速在上层流体中沿垂向分布较均匀, 在波面以下的下层流体中沿垂向分布有衰减的趋势, 但衰减很小,而在两层流体交界面与波谷之间的高度范围内, 水平流速由正变负, 衰减明显; (3)上层流体中的波致水平流速大于下层流体; (4)定义两层流体界面与波谷的水深范围为过渡水深范围, 水平流速在该水深范围内沿垂向衰减明显, 首先由正向衰减至零, 继而反向增大。(5)对比不同振幅下内孤立波波致水平流速, 发现随内孤立波振幅的增大, 过渡水深范围有所增大。

图6 内孤立波波致水平流速沿垂向分布Fig.6 Profiles of magnitude of the horizontal velocity induced by internal solitary waves

4 结论

利用 Fluent软件, 采用“平板拍击”方法, 利用动网格技术, 基于UDF编译功能, 使用KdV、mKdV理论控制造波板的运动速度, 对内孤立波进行数值模拟, 并研究了内孤立波波致流场特性。研究结果表明:

(1) 该方法可以成功模拟内孤立波的生成和传播, 其生成的内孤立波波形与实验结果一致。

(2) 在内孤立波传播过程中, 上层流体的流速始终与内孤立波传播方向一致, 下层流体的流速始终与内孤立波传播方向相反, 说明内孤立波在上、下层产生的流速是单方向的冲击流, 而非振荡流, 且流速的方向在上、下层始终相反形成剪切流。

(3) 对于一个空间固定位置, 内孤立波经过时,上下层流体的波致水平流速先增大后减小, 在波谷经过时, 波致水平流速最大且上层流体中的水平流速大于下层流体。

(4) 波谷经过断面处的内孤立波波致水平流速,在上层流体中沿垂向接近均匀分布, 在波面以下的下层流体中沿水深有较小的衰减趋势。而两层流体界面与波谷的水深范围为过渡水深范围, 水平流速在该水深范围内沿垂向衰减明显, 首先由正向衰减至零, 继而反向增大。

(5) 比较不同振幅下的内孤立波波致水平流速, 发现随内孤立波振幅的增大, 过渡水深范围有所增大。

方欣华, 杜 涛, 2005. 海洋内波基础和中国海内波. 青岛:中国海洋大学出版社, 258—281

孙大鹏, 李玉成, 2000. 数值水槽内的阻尼消波和波浪变形计算. 海洋工程, 18(2): 46—50

杜 涛, 吴 巍, 方欣华, 2001. 海洋内波的产生与分布. 海洋科学, 25(4): 25—28

陈 钰, 朱良生, 2009. 基于Fluent的海洋内孤立波数值水槽模拟. 海洋技术, 28(4): 72—75, 100

柯自明, 尹宝树, 徐振华等, 2009. 南海文昌海域内孤立波特征观测研究. 海洋与湖沼, 40(3): 269—274

徐鑫哲, 2012. 内波生成机理及二维内波数值水槽模型研究.哈尔滨: 哈尔滨工程大学硕士学位论文, 32—34

高原雪, 尤云祥, 王 旭等, 2012. 基于MCC理论的内孤立波数值模拟. 海洋工程, 30(4): 29—36

黄文昊, 尤云祥, 王 旭等, 2013. 有限深两层流体中内孤立波造波实验及其理论模型. 物理学报, 62(8): 084705

董 志, 詹杰民, 2009. 基于VOF方法的数值波浪水槽以及造波、消波方法研究. 水动力学研究进展, 24(1): 15—21

韩 朋, 任 冰, 李雪临等, 2009. 基于VOF方法的不规则波数值波浪水槽的阻尼消波研究. 水道港口, 30(1): 9—13

Buick J M, Martin A J, Cosgrove J A et al, 2003. Comparison of a lattice Boltzmann simulation of steep internal waves and laboratory measurements using particle image velocimetry.European Journal of Mechanics-B/Fluids, 22(1): 27—38

Choi W, Camassa R, 1999. Fully nonlinear internal waves in a two-fluid system. Journal of Fluid Mechanics, 396: 1—36

Helfrich K R, Melville W K, 2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics, 38(1): 395—425

Liu B Q, Yang H, Zhao Z X et al, 2014. Internal solitary wave propagation observed by tandem satellites. Geophysical Research Letters, 41(6): 2077—2085

Michallet H, Barthélemy E, 1998. Experimental study of interfacial solitary waves. Journal of Fluid Mechanics, 366:159—177

Osborne A R, Burch T L, 1980. Internal solitons in the Andaman Sea. Science, 208(4443): 451—460

Wang F, Wu K F, Guo H Y et al, 2015. Experimental study on internal solitary wave induced flow field. In: Xie L Q ed.Advanced Engineering and Technology II. Hong Kong,China: CRC Press, 111

Xu Z H, Yin B S, Hou Y J, 2010. Highly nonlinear internal solitary waves over the continental shelf of the northwestern South China Sea. Chinese Journal of Oceanology and Limnology, 28(5): 1049—1054

Zhang L, Wang L L, Yu Z Z et al, 2012. Characteristics of nonlinear internal waves in a three-dimensional numerical wave tank. Applied Mechanics and Materials, 212—213: 1123—1130