双喷嘴挡板伺服阀工作过程的数值模拟

2016-01-15胡均平,李科军

振动与冲击 2015年15期

双喷嘴挡板伺服阀工作过程的数值模拟

胡均平，李科军

(中南大学机电工程学院，长沙410083)

摘要：为从理论上研究双喷嘴挡板伺服阀的工作性能，需对其建立较为精确的数学模型。针对电液伺服阀工作过程固有的机电液耦合特性，选择可统一处理多能域复杂系统的键合图法作为建模工具。根据衔铁、挡板组件和阀芯的运动规律，考虑喷嘴射流液动力等非线性因素，采用集中参数构建了系统的键合图模型，并推导出描述伺服阀工作过程内部能量供给、传递、转化和消耗的状态方程。结合某型伺服阀的相关参数，采用四阶Runge-Kutta法进行数值求解。数值模拟结果表明：伺服阀输入阶跃电流后，预测的负载流量阶跃响应的变化趋势能与试验结果较好吻合，并且模型能预测伺服阀系统内部状态变量的动态特性，为伺服阀结构参数优化研究和动态性能分析提供了理论依据。

关键词：双喷嘴挡板伺服阀；键合图；耦合；数值模拟；动态特性

中图分类号:TH137.5文献标志码：A

基金项目：国家高技术研究发展计划(863计划，2014AA041501)资助项目

收稿日期：2014-06-24修改稿收到日期：2014-07-30

Numerical simulation for a twin-flapper-nozzle servo valve’s working process

HUJun-ping,LIKe-jun(College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract:To investigate the working performance of a twin-flapper-nozzle servo valve in theory, its accurate mathematical model needs to be established. According to electromechanical coupled characteristics of a servo valve, the bond graph method was taken as the modeling tool with advantages for dealing with multi-energy domain complex systems. According to the geometric relationship among the armature, baffle components and the main valve, the bond graph model of the servo valve was constructed based on its working mechanism, the nozzle jet fluid power and other nonlinear factors, and the system state-equations describing the energy input, transfer, translation and dissipation of the servo valve were deduced. Numerical simulation based on the four order Runge-Kutta method was performed with relavant parameters of a certain type of servo valve. The results showed that the trend of the load flow rate step response agrees well with that of the experimental results, the dynamic characteristics of the system internal state variables can be predicted with the model, so this modeling method provides a theoretical basis for the optimal design and dynamic analysis of servo valves.

Key words:twin-flapper-nozzle servo valve; bond graph; coupling; numerical simulation; dynamic characteristics

双喷嘴挡板伺服阀由于具有动态响应速度快、控制精度高、结构紧凑等优点，广泛应用于工业上，如测试装置，自动生产流水线、工程机械等设备中[1]。伺服阀作为伺服系统的核心元件，与其它液压部件的匹配和控制直接影响整个系统的工作性能，因而得到了广泛的研究，但多侧重于单方面的特性，如针对伺服系统控制策略、控制理论的研究[2-5]；或力矩马达的电磁回路动态特性[6]、反馈弹簧组件强度[7]及力矩马达谐响应分析[8]等结构方面的特性；或新材料、新结构在伺服阀上的应用[9-10]。随着近代工业的发展，要求伺服阀输出平稳流量以满足系统高速高精高效的性能要求，因此建立准确的数学模型，对伺服阀进行参数、性能优化和搭建伺服系统的全局模型显得非常重要。双喷嘴挡板伺服阀是一个机电液耦合的系统，传统的单独针对电磁系统或液压系统的建模与分析很难实现系统整体性能最优，特别是对于机电液系统较为复杂，考虑因素较多，且存在非线性的情况，传统的传递函数法相当繁琐，且往往难以实现，甚至无效[11-15]。键合图法为该问题的解决提供了颇具特色的途径[16-18]，它可以直接基于物理描述对多域系统使用相同的符号进行可视化建模，基于此模型可方便地获得系统的状态方程，并借助计算机实现系统的动态特性分析。文中采用功率键合图法，从双喷嘴挡板伺服阀具体工作机理出发，考虑喷嘴射流液动力等非线性因素，精确分析了伺服阀功率流分布形式，快速、准确地构建了伺服阀的计算模型。

1双喷嘴挡板伺服阀结构原理

图1为双喷嘴挡板伺服阀的结构原理图，该阀主要由上部的永磁式力矩马达和下部的液压放大部分组成，两者通过挡板反馈杆的力反馈建立协调关系。无控制电流时，衔铁5处于上、下永久磁体3的中间位置，挡板8也处于两喷嘴的中间位置，主阀阀芯11在反馈杆9端部小球的约束下处于中位，阀无液流输出。当有电流i输入时，衔铁5产生顺时针方向的电磁力矩，使弹簧管7和反馈杆9产生变形，挡板偏离中位，改变了喷嘴挡板左、右间隙，引起主阀阀芯11左、右腔产生控制压差，推动主阀阀芯右移，同时带动反馈杆端部小球右移，使反馈杆进一步变形。最后，反馈杆9和弹簧管7变形产生的反力矩、电磁力矩、喷嘴液流作用于挡板的力矩等诸力矩达到平衡时，主阀阀芯停止运动，衔铁、挡板组件回复中位。

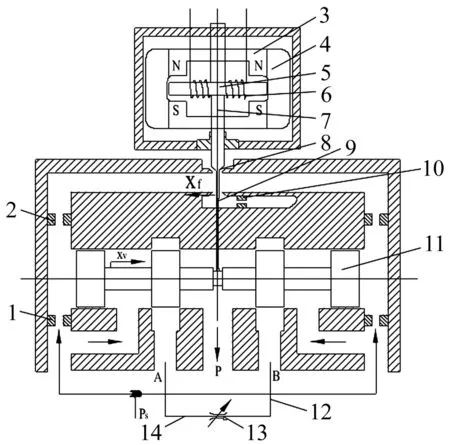
1.阻尼孔3；2.阻尼孔2；3.永久磁铁；4.导磁体；5.衔铁；6.电磁线圈；7.弹簧管；8.挡板和喷嘴；9.反馈杆；10.阻尼孔1；11.主阀阀芯；12.管路2；13.可调节流阀；14.管路1 图1　双喷嘴挡板伺服阀结构原理图 Fig.1 The structure principle of twin flapper-nozzle servo-valve

2双喷嘴挡板伺服阀建模

根据图1的电液伺服阀结构特点，将其分为两个子系统：第一级子系统(电气部分)，包括力矩马达、喷嘴挡板、弹簧管等；第二级子系统(液压部分)，包括反馈杆、主阀芯、阻尼孔等。采用功率键合图分别建立各子系统的键合图模型，进而建立整个伺服阀的键合图模型，在建模前需做以下简化：

(1)伺服阀入口压力恒定，出口压力为零；

(2)采用集中参数法处理液阻、液容、质量；

(3)在主阀阀芯开启的运动过程中只考虑稳态液动力，忽略瞬态液动力。

2.1第一级子系统建模

(1)

图2　衔铁、挡板组件运动规律 Fig.2 The motion relation of armature, baffle component

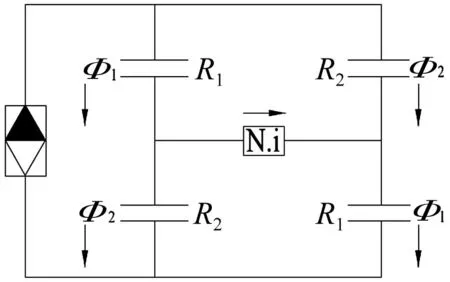
图3　力矩马达的磁路原理图 Fig.3 The principle diagram of magnetic circuit of torque motor

图3为力矩马达磁路的工作原理，经分析可知，该磁路是对称桥路，通过对角臂的磁通(即通过对角线上相对气隙的磁通)是相等的，由于环绕每个回路的磁动势之和必须等于0，本文选择包含对角桥臂的两个磁动势的回路作为研究对象，其等效键合图模型见图4，根据衔铁、挡板组件的运动规律可知：

当衔铁位置变化时，磁阻R1、R2为

(2)

(3)

式中：R0为衔铁在中间位置时的磁阻；e为衔铁在中间位置时，气隙的长度；S为气隙处的导磁体工作面积；μ0为导磁率；其中z2=-z1；

两磁通分别为

(4)

(5)

式中：N为线圈的匝数、E0为电磁铁的磁动势。

力矩马达产生的力矩为

(6)

将式(4)、式(5)代入式(6)得

(7)

式(7)经线性化处理可以得到

CTM=K1i+Kma

(8)

文献[2]给出了弹性体弯曲变形与力矩、力的关系

(9)

联合式(1)和式(9)有

(10)

由上式可知，可以用二通口C场键元表示弹簧管施加的力矩和力。

根据式(1)、式(8)和式(10)，应用键合图建模规则，可以很容易得到图4所示的第一级子系统的键合图模型。键合图模型中的功率流向(键的箭头指向)根据实际模型逐一画出，各键合图元的因果关系按照键合图规则标注。

图4　第一级子系统键合图模型 Fig.4 The bond graph model of the first level subsystem

Kwd3((xg-d3a)-xmv)+f2d2、

(11)

K11d1)a)-Kw((xg-d3a)+xmv)

(12)

2.2第二级子系统建模

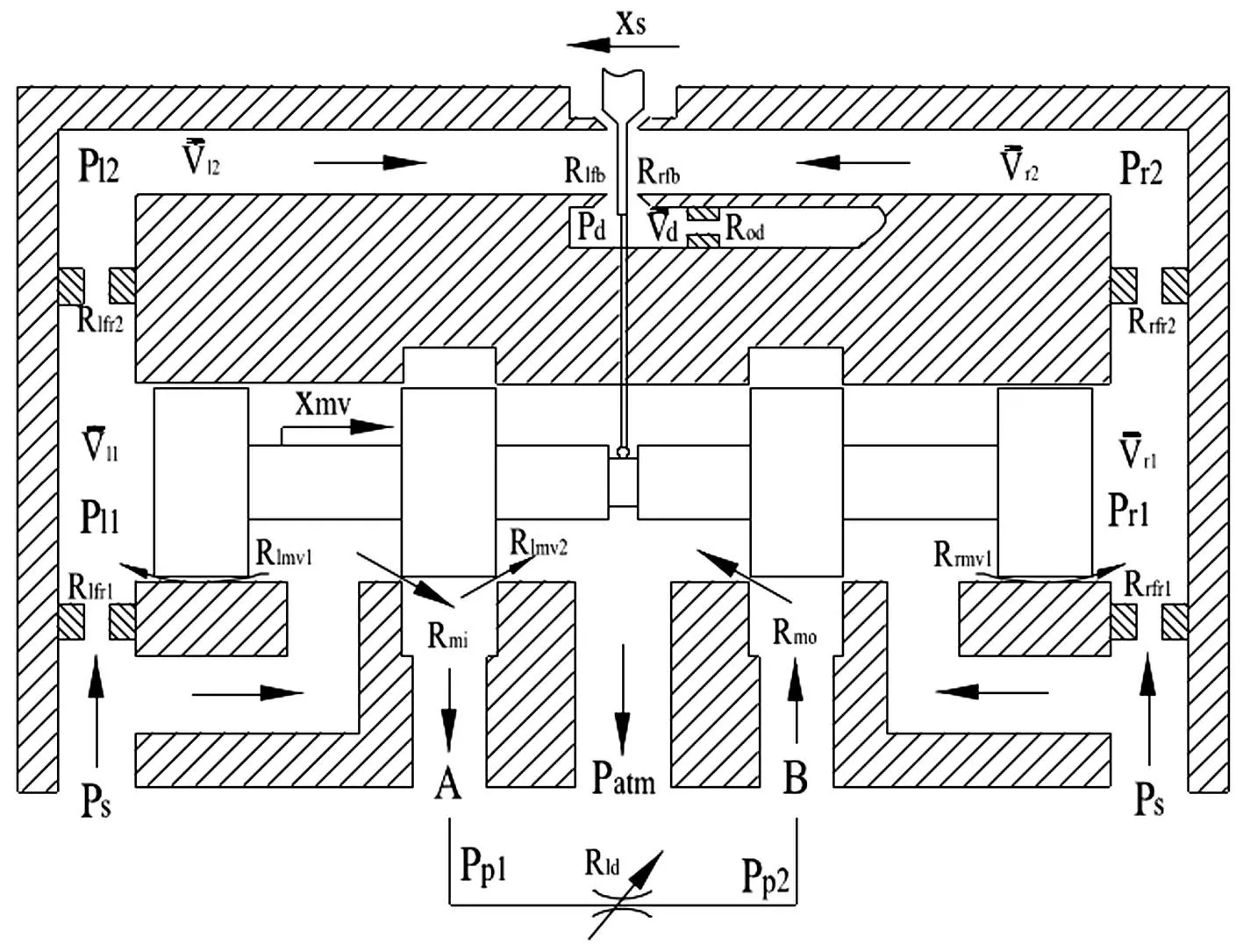
图5　第二级子系统结构简图 Fig.5 The structure diagram of the second subsystem

图6　第二级子系统键合图模型 Fig.6 The bond graph model of the second subsystem

各个容腔的流量变化为

(14)

(15)

(16)

(17)

(18)

(19)

(20)

主阀阀芯上的惯性力为

(21)

作用在喷嘴处挡板的力为

f2=fi-(Pl2-Pr2)Afl-Ff

(22)

式中：Ff为作用在挡板上的液动力；fi为挡板运动到极限位置和喷嘴接触时引起的弹性接触力；其计算公式分别如下[1]

(23)

(24)

式中：Kis为冲击刚度系数；xf为喷嘴处挡板移动的距离；x0为挡板处于中心位置时；挡板喷嘴之间的距离。

各个容腔的压力可分别表示为：

Pl1=Kl1Vl1；Pl2=Kl2Vl2；Pd=KdVd；

Pr2=Kr2Vr2；Pr1=Kr1Vr1；Pp1=Kp1Vp1；Pp2=Kp2Vp2

2.3伺服阀键合图模型

根据反馈杆和主阀阀芯的位移协调关系及功率流的传递方向，将图4、图6两个子系统模块联合起来建立图7所示的伺服阀系统的键合图模型。该模型可直观地揭示伺服阀的运动规律，也明确了系统所包含的所有变量，真实反映出伺服阀内部能量分配、传递、消耗和储存的情况。其中，喷嘴挡板、节流孔、阀口等处的液阻都是导纳型因果关系，而且喷嘴挡板、阀口处的液阻和开口面积有关，流过各液阻流量的具体计算公式可参考文献[1]。

图7　双喷嘴挡板伺服阀键合图模型 Fig.7 The bond graph model of twin flapper-nozzle servo valve

3仿真分析

将以上导出的状态方程转化为计算机Matlab仿真模型时，对于时变非线性液阻和阀芯位移等约束条件的表达，可分别编写条件转移结构语句来处理，采用四阶龙格—库塔法运算程序进行计算。以某型伺服阀为研究对象，仿真中用到的主要参数见表1。

为验证模型的合理性和准确性，参考电液流量伺服阀测试标准HB5610-88进行了负载流量阶跃响应试验。试验结果如图11所示，其中实线部分为仿真结果，虚线部分为试验结果。由此可以看出，和仿真曲线相比，试验曲线的峰值时间为14 ms，增加2 ms左右，经过一定时间振荡后，两者达到稳定状态的调节时间基本一致，都是32 ms左右，但试验稳态流量值减小了1.5 L/min。导致此差异的原因是多方面的，如计算过程中假设的输入压力为定值、传感器测量误差、参数取值误差和计算式的误差等，这些都对计算结果造成了实际影响。如果选用更高性能的传感器或利用试验曲线进行参数辨识，将得到与实验结果更接近的仿真曲线。从整个比较结果看，仿真计算具有相当的精度，说明了该模型的有效性。

表1　仿真的基本参数

除了模拟伺服阀负载流量阶跃变化外,该模型还可以仿真各工作腔的压力变化、阀芯的运动变化、衔铁转矩变化、反馈弹簧作用力情况等, 对伺服阀内部状态变量的动态特性进行全面预测，也可分析主要参数对系统工作性能的影响。

图12～图15给出了输入阶跃电流时，伺服阀衔铁转矩、反馈杆作用力及主阀阀芯位移的变化规律，可以发现这些参数很难实时测量，但可通过数值模拟分析其变化规律。从图中曲线可以看出，当输入阶跃电流时，在1 ms时，衔铁转矩达到最大值0.077 N·m，同时衔铁、喷嘴挡板达到极限位置，在0～1 ms内，主阀芯位移变化不大,说明衔铁转矩的主要起调整挡板与喷嘴之间间隙的作用，而不是直接控制主阀芯运动的决定因素；在1～8 ms内，衔铁转角、衔铁转矩无明显变化，但因喷嘴挡板两边间隙改变，主阀芯左右腔油液压差发生变化，主阀阀芯做加速运动，反馈杆端部小球随之一起运动，反馈杆变形量进一步增大，在8 ms时，反馈杆变形引起的力矩能克服衔铁转矩使衔铁、挡板组件向中心位置移动，在55 ms时，衔铁转矩稳定在0.032 N.m左右，反馈杆作用力稳定在1.24 N左右，主阀芯位移稳定在3.2 mm左右，系统达到平衡状态。从以上分析可知，伺服阀的工作性能还有提升的空间，可以通过修改模型参数进行优化，限于篇幅，将另文论述。

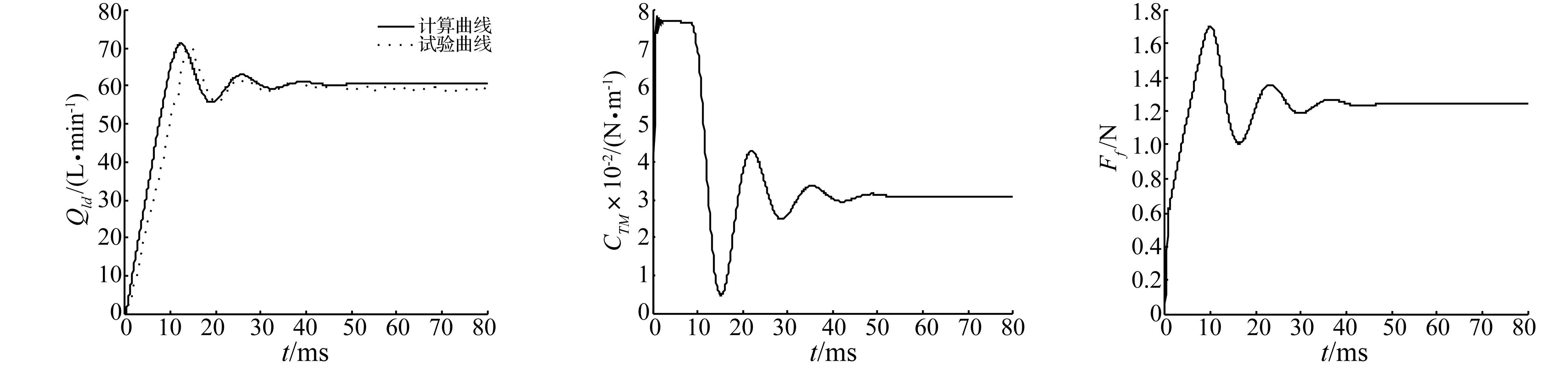
图11 流量阶跃响应Fig.11Theflowstepresponse图12 衔铁转矩阶跃响应Fig.12Thearmaturetorquestepresponse图13 反馈杆作用力阶跃响应Fig.13Theforceoffeedbackstemstepresponse

图14　主阀芯位移阶跃响应 Fig.14 The displacement of main valve core step response

图15　衔铁转角阶跃响应 Fig.15 The armature angle step response

4结论

(1)本文从双喷嘴挡板伺服阀具体工作机理出发，根据伺服阀工作时各能域作用的耦合关系，将其划分为两个子系统，利用键合图对多种能量范畴的系统一体化建模的优势，建立了伺服阀的键合图模型，按照键合图规则直接列写了状态方程，并通过试验证明该模型的正确性。利用该模型可以深入研究伺服阀的工作性能及动态特性，同时通过修改参数可以得知特定结构对整个伺服阀性能的影响，为伺服阀参数、性能优化提供了理论依据。

(2)利用键合图模型良好的扩展性和通用性，可考虑将该伺服阀键合图模型作为独立的子模型，添加到其它包含伺服阀的液压控制系统中，实现复杂系统的性能预测与动态分析，这方面的研究将另文论述。

参考文献

[1]Merritt H. Hydraulic Control System[M]. New York:John Wiley & Sons,1967.

[2]王勇勤，张云飞，严兴春,等．伺服阀非线性特性建模的液压弯辊系统动态特性[J]．重庆大学学报，2005，28 (11)：5-7．

WANG Yong-qin, ZHANG Yun-fei, YAN Xing-chun, et al. Nonlinear characteristic modeling of servo valve on hydraulic bending roll system’s dynamic characteristic[J].Journal of Chongqing University, 2005, 28 (11): 5-7．

[3]李素玲, 刘军营. 变截面板簧轧机电液伺服系统性能分析[J]. 农业机械学报, 2007, 38(9): 171-174.

LI Su-ling, LIU Jun-ying. Performance analysis of electro-hydraulics servo system of automobile leaf spring rolling mill[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(9): 171-174.

[4]江桂云，王勇勤，严兴春. 液压伺服阀控缸动态特性数学建模及仿真分析[J]. 四川大学学报, 2008, 40(5): 690-693.

JIANG Gui-yun, WANG Yong-qing, YAN Xin-chun. Mathematics modeling and simulation analysis of dynamic characteristics for hydraulic cylinder controlled by servo valve[J]. Journal of Si Chuan University, 2008, 40(5):690-693.

[5]郎需林，王永强，张承瑞，等. Delta机构伺服系统模型参考自适应建模[J]. 振动与冲击, 2013, 32(19):57-62.

LANG Xu-lin, WANG Yong-qiang, ZHANG Cheng-rui, et al. A model reference adaptive system modeling method for a Delta mechanism servo motor system[J]. Journal of Vibration and Shock, 2013, 32(19):57-62.

[6]Urata E. Study of magnetic circuits for servo-valve torque motors[C]//Bath Workshop on Power Transmission and Control (PTMC). Bath: U.K, 2000:269-282.

[7]赵开宇，袁朝辉，张颖. 射流管式伺服阀反馈弹簧组件分析[J],中国机械工程，2013,24(19)：2606-2610.

ZHAO Kai-yu, YUAN Zhao-hui, ZHANG Ying. Analysis of jet pipe servo valve feedback spring components[J],China Mechanical Engineering, 2013,24(19)：2606-2610.

[8]彭敬辉, 李松晶, JACOB M M. 电磁力与射流流场中压力脉动作用下伺服阀力矩马达谐响应分析[J]. 工程力学, 2012, 30(2)：348-353.

PENG Jing-hui, LI Song-jing, JACOB M M. Harmonic response analysis of a hydraulic servo-valve torque motor under the action of electromagnetic force and pressure fluctuation in jet flow field[J]. Engineering Mechanics, 2012, 30(2): 348-353.

[9]曲兴田, 鄂世举, 吴博达, 等. 双压电晶片驱动喷嘴挡板式伺服阀[J]. 吉林大学学报：工学版, 2005, 35(2)：153-156.

QU Xing-tian, E Shi-ju, WU Bo-da, etal. Nozzle2Flapper Servo2Valve driven by piezoelectric bimorph[J]. Journal of Jilin University, 2005, 35(2): 153-156.

[10]李松晶，鲍文. 磁流体对伺服阀力矩马达动态特性的影响[J]. 机械工程学报，2008, 44(12)：137-142.

LI Song-jing, BAO Wen．Influence on dynamic characteristics of a hydraulic servo-valve torque motor due to magnetic fluids[J]. Chinese Journal of Mechanical Engineering, 2008, 44(12)：137-142.

[11]孙萌，李长春，延皓,等. 阀控非对称缸位置系统的非线性建模[J]. 北京交通大学学报，2012, 36(4)：164-168.

SUN Meng, LI Chang-chun, YAN Hao, et al. Nonlinear modeling for valve controlled asymmetric cylinder position system[J]. Journal of Beijing Jiaotong University, 2012, 36(4): 164-168.

[12]母东杰，李长春，延皓等. 双喷嘴挡板伺服阀非线性建模及其线性化[J]. 机械工程学报，2012，48(2)：193-198.

MU Dong-jie, LI Chang-chun, YAN Hao, et al. Nonlinear simulation and linearization of twin flapper-nozzle servo vave[J]. Chinese Journal of Mechanical Engineering, 2012, 48(2): 193-198.

[13]Ghasemi E, Jazayeri S A, Moosavian S A A. Model improvement for a servo valve with force feedback and back pressure[C]//Robotics, Automation and Mechatronics, 2008 IEEE Conference on. IEEE, 2008: 895-900.

[14]Anyi H, Yiming R, Zhongfu Z, et al. Identification and adaptive control for electro-hydraulic servo system using neural networks[C]//Intelligent Processing Systems, 1997. ICIPS’97. 1997 IEEE InternationalConference on. IEEE, 1997, 1: 688-692.

[15]Kovari A. Influence of cylinder leakage on dynamic behavior of electrohydraulic servo system[C]//Intelligent Systems and Informatics, 2009. SISY’09. 7th International Symposium on. IEEE, 2009: 375-379.

[16]Karnopp D C，Margolis D L，Rosenberg R C．System Dynamics：modeling and simulation of mechatronic systems[M].Hoboken, NJ: Wiley, 2006.

[17]Dasgupta K, Murrenhoff H. Modelling and dynamics of a servo-valve controlled hydraulic motor by bond graph[J]. Mechanism and Machine Theory, 2011, 46(7): 1016-1035.

[18]Dasgupta K, Watton J, Pan S. Open-loop dynamic performance of a servo-valve controlled motor transmission system with pump loading using steady-state characteristics[J]. Mechanism and Machine Theory, 2006, 41(3): 262-282.