圆形刚性承载板载荷作用下双参数地基上多层矩形板的动力响应

第一作者张震东男，博士生，1988年生

通信作者马大为男，教授，博士生导师，1953年生

圆形刚性承载板载荷作用下双参数地基上多层矩形板的动力响应

张震东，马大为，何强，朱忠领

(南京理工大学机械工程学院，南京210094)

摘要：提出一种考虑水平阻尼的双参数地基模型，推导了此地基模型上多层矩形板的中性面位置表达式，建立水平动载荷与垂向动载荷联合作用下多层地基板内力平衡方程，并在此基础上给出了板的运动微分方程。采用级数分解和Laplace积分变换相结合的方法，求解了圆形刚性承载板载荷作用下多层地基板的挠度解析表达式。在MATLAB软件中编写计算程序，以三层地基板为例深入分析了水平阻尼系数、摩擦系数、运动方向对板动力响应的影响。研究表明，随着水平阻尼系数的增大，板的挠度逐步减小，摩擦系数和运动方向对载荷作用面圆心处的动力响应几乎没有影响，而对远离圆心处点的挠度影响较大。

关键词：圆形刚性承载板；水平阻尼系数；双参数地基模型；多层板；水平动载荷；垂向动载荷

基金项目：国防基础科研(B2620110005)

收稿日期：2014-06-19修改稿收到日期：2014-08-14

中图分类号:TJ768.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.033

Abstract:A two-parameter foundation model was proposed considering horizontal damping. Then the displacement expressions of neutral layer plane of a multi-layer rectangular plate on the foundation model were deduced. In order to get the motion differential equation of the plate, its internal force equilibrium equations were built under the combined action of horizontal dynamic load and vertical dynamic one. Then the analytical expression of the plate deflection under a circular rigid bearing plate’s load was solved with the combination of Laplace integral transformation and the triangular series methods. The influences of horizontal damping coefficient, friction coefficient and motion direction on the dynamic response of the plate were analyzed by using MATLAB software and taking a three-layer plate as an example. Results indicated that the deflection of the plate decreases gradually with increase in horizontal damping coefficient; the friction coefficient and motion direction have a greater influence on the deflection of the point far from the circuar plate center, but their effects on the dynamic response of the circular plate center can be ignored.

Dynamic response of a multi-layer rectangular plate on a two-parameter foundation under a circular rigid bearing plate’s load

ZHANGZhen-dong,MADa-wei,HEQiang,ZHUZhong-ling(College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China )

Key words:circular rigid bearing plate; horizontal damping coefficient; two-parameter foundation model; multi-layer plate; horizontal dynamic load; vertical dynamic load

导弹发射过程中，发射装备对地载荷通过圆形支撑盘传递至路面，路面在动载荷下的响应又会影响到发射装备的稳定性，最终干扰导弹出筒姿态，甚至导致导弹发射失败，可见路面在圆形支撑盘对地载荷下的动力响应具有很高的研究价值和实用价值。经验表明，导弹发射过程中发射装备不停振动，圆形支撑盘不可避免地存在水平移动，产生水平动载荷，故圆形支撑盘对地载荷由垂向动载荷、水平动载荷构成。由于圆形支撑盘刚度远大于路面，因此可将支撑盘视为圆形刚性承载板。对于路面则可采用双参数地基上的板模型表示。

针对地基上板的动力响应问题，国内外学者开展了许多研究，Fryba[1]研究了移动荷载作用下Kelvin地基上无限大板挠度的解析表达式；孙璐等[2]、蒋建群等[3]、姚海林等[4]均采用积分变换的方法给出了弹性地基上无限大板在匀速移动载荷作用下的积分形式解，卢正等[5]分析了黏弹性地基板在矩形变速荷载作用下路面的动态挠度，但以上研究仅分析了单层板的动力响应；李皓玉等[6]将路面视为黏弹性地基上无限大双层板，获得了车辆载荷作用下路面动力响应解析解；文献[2-6]均将道路视为无限大板与路面实际结构不符，为了弥补上述不足，颜可珍等[7-8]将路面视为无限长地基板，分析了运动常值均布载荷和简谐载荷作用下板的动力响应。在矩形板动力响应方面，郑小平等[9]、颜可珍等[10]采用级数分解的方法研究了黏弹性地基上矩形板在运动载荷下的动态响应问题，寇磊等[11]利用分数微分得到了黏弹性地基双参数模型，分析了冲击载荷下分数阶微分地基模型上矩形板的动力响应。

以上研究只关注垂向动载荷作用下板动力响应，而对于水平动载荷与垂向动载荷联合作用下多层地基板的动力响应问题，鲜有报道。本文提出一种考虑水平阻尼的双参数地基模型，推导了此地基模型上多层Kirchhoff薄板在水平动载荷、垂向动载荷联合作用下的运动微分方程，分析了水平阻尼系数、摩擦系数、运动方向对板动力响应的影响。

1双参数地基上的多层矩形板模型

圆形刚性承载板载荷作用下多层矩形地基板模型见图1(a)、图1(b)，模型中刚性板在多层地基板上表面缓慢移动，移动方向与x轴夹角为θ，故多层板不仅承受刚性板垂向载荷Fv(x,y,t)，而且受到刚性板水平移动引起的水平动载荷作用，水平动载荷x轴分量为Fhx(x,y,t)，y轴分量为Fhy(x,y,t)，见图1(b)。由于板的厚宽比很小，故认为多层板在刚性板载荷作用下的变形，仍然服从Kirchhoff薄板假设。

图1　多层矩形板模型及地基模型 Fig.1 Multi-layer rectangle plate model and foundation model

文献[12]提出了一种计及地基水平反力的双参数地基模型，并研究了此地基模型上无限大板的动力响应。为进一步丰富前人的研究工作，本文给出了考虑水平阻尼的双参数地基模型，见图1(a)。该模型采用四个独立的参数表征地基土的特性，分别为水平剪切系数kh，水平阻尼系数Ch，压缩系数kv，垂向阻尼系数Cv。

此地基模型的水平方向地基反力，可由下式求出：

(1)

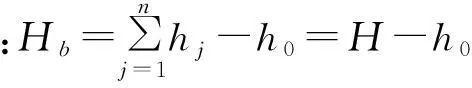
2地基上多层板的运动微分方程

2.1中性面位置求解

文献[13]假设板间的结合状态为完全连续，给出了双层板中性面位置的表达式，本文在此基础上求解多层板的中性面位置。

由下式可得到每层板中应力：

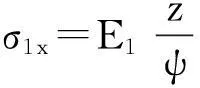
(2)

式中:Ei为每层板的弹性模量；ψ为中性面曲率。

由中性面上应力为零条件，得到：

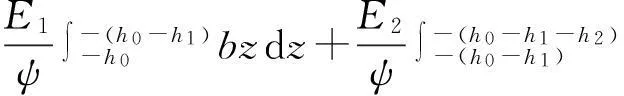
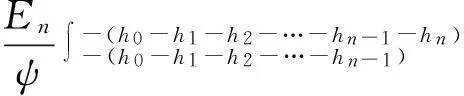
(3)

式中:hj(j=1～n)为每层板的厚度；h0为中性面至多层板上表面距离；b为板宽。

将上式积分展开，得到中性面距多层板上表面距离，如下：

(4)

2.2多层板中横截面上的内力

从多层板中截出底边为dx，dy，高为H的微小六面体为研究对象，其中x截面上弯矩Mx，y截面上弯矩My，x截面上扭矩Mxy及y截面上扭矩Myx，表达式如下：

(5)

式中:

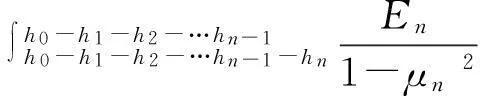
(6)

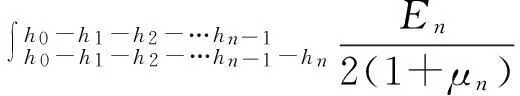
其中:μj(j=1～n)为每层板的泊松比。

2.3运动微分方程

考虑到薄板小挠度变形，多层板z方向力的平衡方程为：

(7)

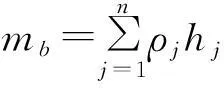
分别取x轴，y轴力矩平衡，推导出下列平衡方程：

Fhy(x,y,t)·h0=Qy

Fhx(x,y,t)·h0=Qx

(8)

式中:Fhx(x,y,t)，Fhy(x,y,t)分别为多层板上表面水平方向作用力在x方向，y方向分量。

将式(1)代入式(8)后，上式两边取y的一次微分，下式两边取x的一次微分：

(9)

将式(9)中上、下两式相加并代入式(7)，得：

(10)

将式(5)代入式(10)，并简化得到式(11)，即水平动载荷与垂向动载荷联合作用下，本文地基模型上多层板的运动微分方程。

(11)

3微分方程求解

3.1垂向动载荷模型

忽略刚性板的缓慢移动对载荷作用面位置的影响，则圆形刚性承载板下垂向载荷表达式，如下[14]

H{r2-[(x-x0)2+(y-y0)2]}

(12)

式中:f(t)为承载板上载荷平均集度；r为载荷圆形分布区域半径；(x0，y0)为圆心坐标；H(x,y)为Heaviside阶跃函数。由上式可以看出当接近承载板载荷边界时，载荷趋于无穷大，与实际情况不相符，计算无法进行。为此，取(x-x0)2+(y-y0)2=(0.99r)2=r02围成的形区域为研究对象，则垂向载荷模型化为：

H{r02-[(x-x0)2+(y-y0)2]}

(13)

3.2水平方向动载荷模型

水平方向动载荷为刚性板对多层板上表面的动摩擦力，则x方向上分量的表达式为：

Fhx(x,y,t)=Fv(x,y,t)λcosθ=

H{r02-[(x-x0)2+(y-y0)2]}

(14)

式中:λ为动摩擦系数，θ为刚性板移动方向与x轴夹角。

同理，y方向上分量的表达式，如下：

Fhy(x,y,t)=Fv(x,y,t)λsinθ=

H{r02-[(x-x0)2+(y-y0)2]}

(15)

将式(13)，式(14)，式(15)代入式(11)等号右端并简化，得：

H{r02-[(x-x0)2+(y-y0)2]}+

(16)

式中:δ(x,y)为Dirac函数。

将上式代入运动微分方程式(11)，得到：

(17)

3.3多层板边界条件

假设多层板四边简支，则边界条件可表示为：

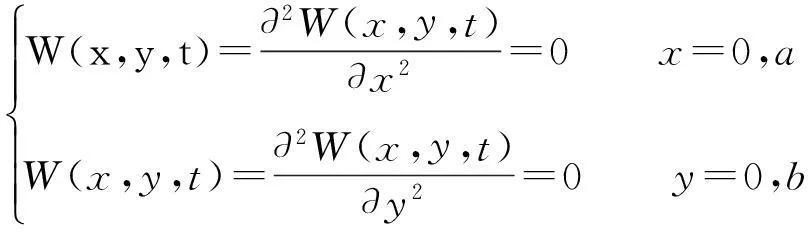
(18)

3.4运动微分方程求解

为满足边界条件，将板的挠度表示为三角级数形式[15]：

(19)

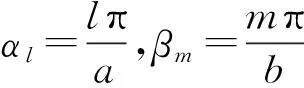
将载荷函数同样展开成三角级数[15]：

(20)

利用三角函数的正交性，求得：

将式(16)代入上式并利用Heaviside阶跃函数性质及Dirac函数性质进行简化得到：

(21)

式中:

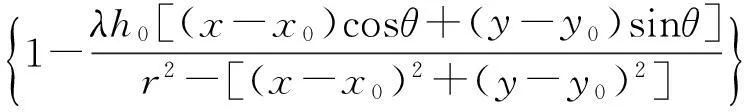
(22)

式中:A为力作用面围成的封闭区域。

将式(19)、式(20)代入式(17)，得到下列二阶微分方程：

qlm(t)=flm(x,y,t)

(23)

令

(24)

将式(24)代入式(23)，得：

qlm(t)″+2ζlmωlmqlm(t)′+

(25)

对式(25)进行Laplace变换，得到：

(26)

进一步简化，可得：

(27)

式中:

(28)

将式(28)代入式(27)并进行Laplace逆变换，得：

(29)

式中:i为虚数单位。

把式(29)代入式(19)可得圆形刚性承载板载荷作用下的板的挠度：

(30)

4算例及参数影响分析

由于文献[15]已经对水平剪切系数，压缩系数、垂向阻尼系数以及板的相关参数对板动力响应的影响做了详细讨论并阐明了影响规律，作者若再进行分析，与前人工作有所重复；另外水平阻尼系数、摩擦系数、运动方向角三个参数与本文的创新之处密切相关，故根据前面推导的结果，以地基上三层板为例，本文仅分析水平阻尼系数Ch、摩擦系数λ、运动方向角θ三个参数对场坪垂向位移的影响，除上述3个参数外，其余参数取值如表1。

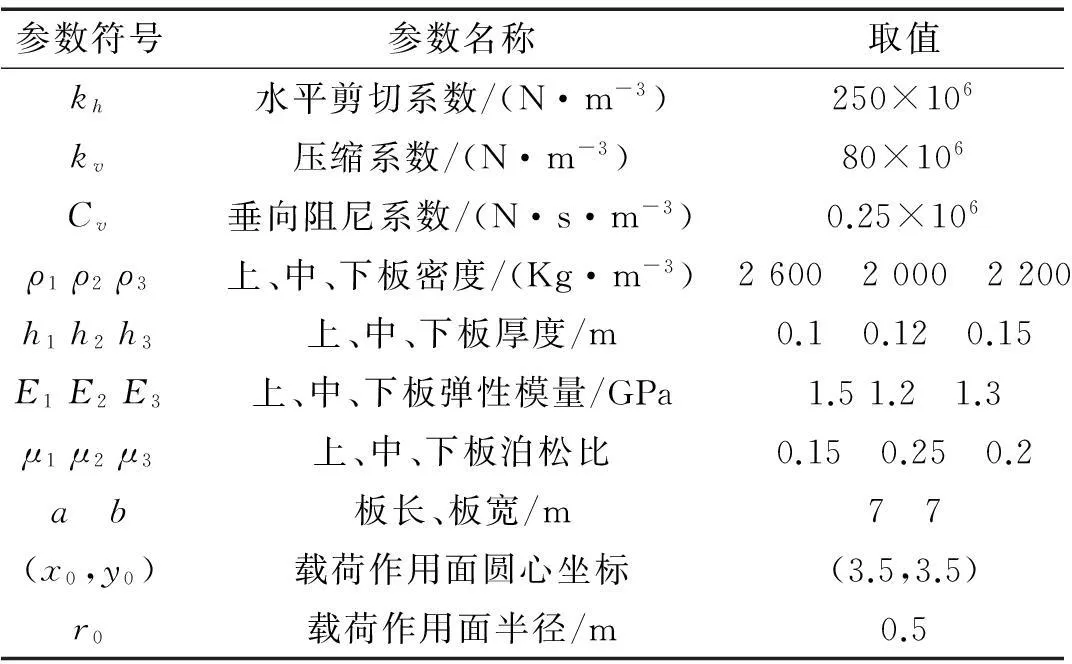
表1　参数取值

为方便说明地基板挠度变化规律，取7个典型点处的下沉量进行分析，典型点在板中位置如图2所示。

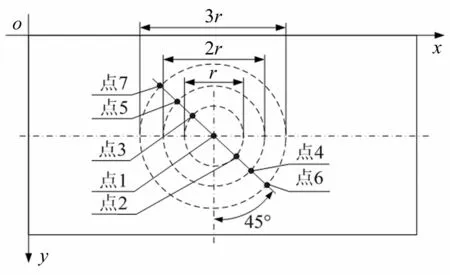
图2　典型点位置 Fig.2 Location of typical points

由于式(30)很难通过Laplace逆变换得到时域解析解，故采用数值Laplace逆变换的方法进行求解，具体是使用Fourier级数展开法快速地求解数值逆Laplace变换，在MATLAB软件中编写相关程序进行数值计算。

承载板上载荷平均集度f(t)变化规律如图3所示。

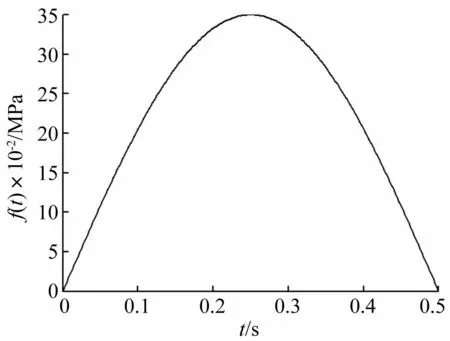
图3　载荷平均集度变化规律 Fig.3 Variation law of load average collection

4.1水平阻尼系数Ch对挠度的影响

计算时取摩擦系数λ=0.5，运动方向θ为45°，水平阻尼系数Ch单位为：N·s/m3。

由于篇幅限制，图4～图6只给出了不同水平阻尼系数Ch时，点1、点2、点3处垂向位移的变化规律，其余点的变化规律与此3个点相似。

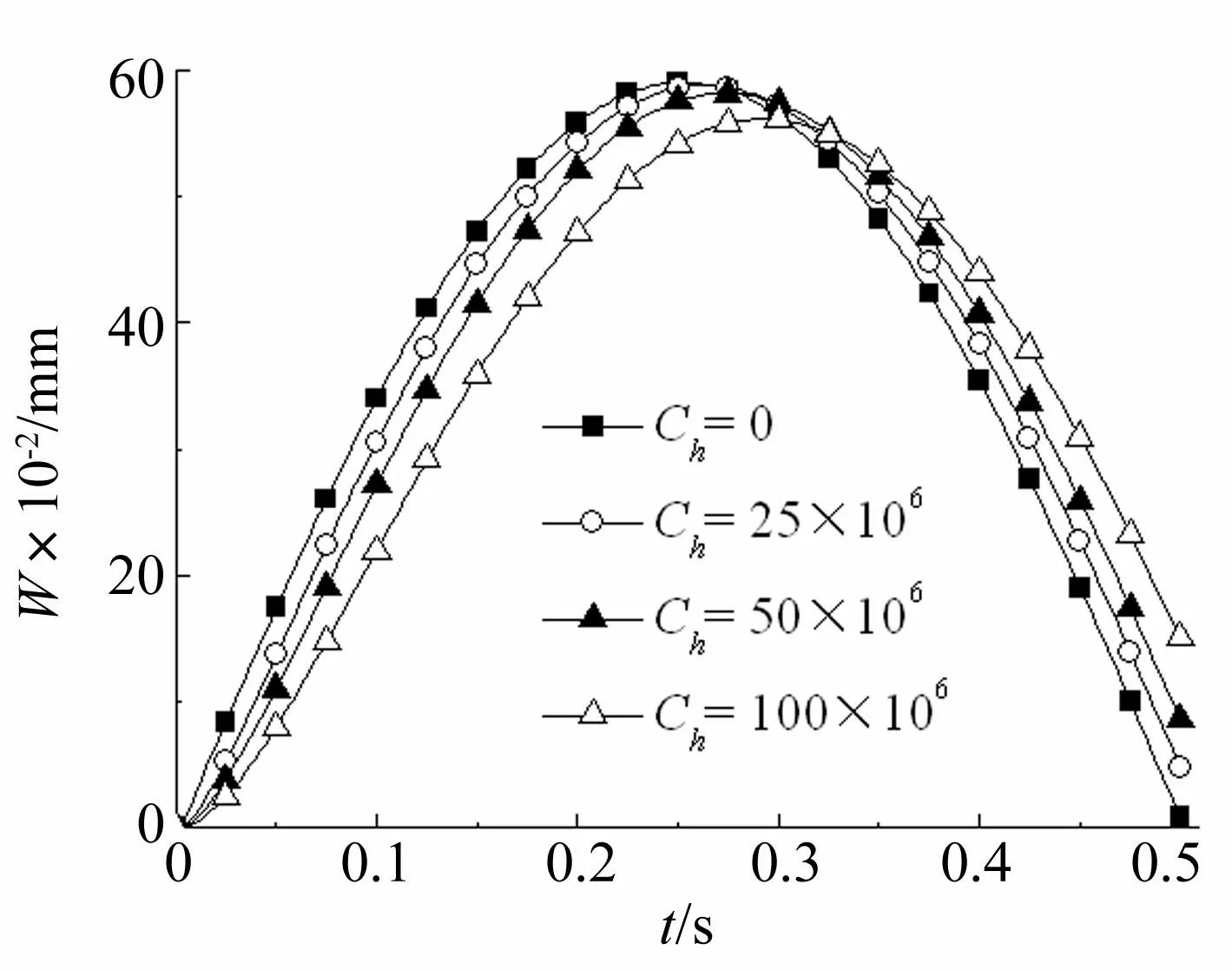
图4　不同水平阻尼系数时点1处挠度变化曲线 Fig.4 The deflection curves of point 1 under different horizontal damping coefficient values

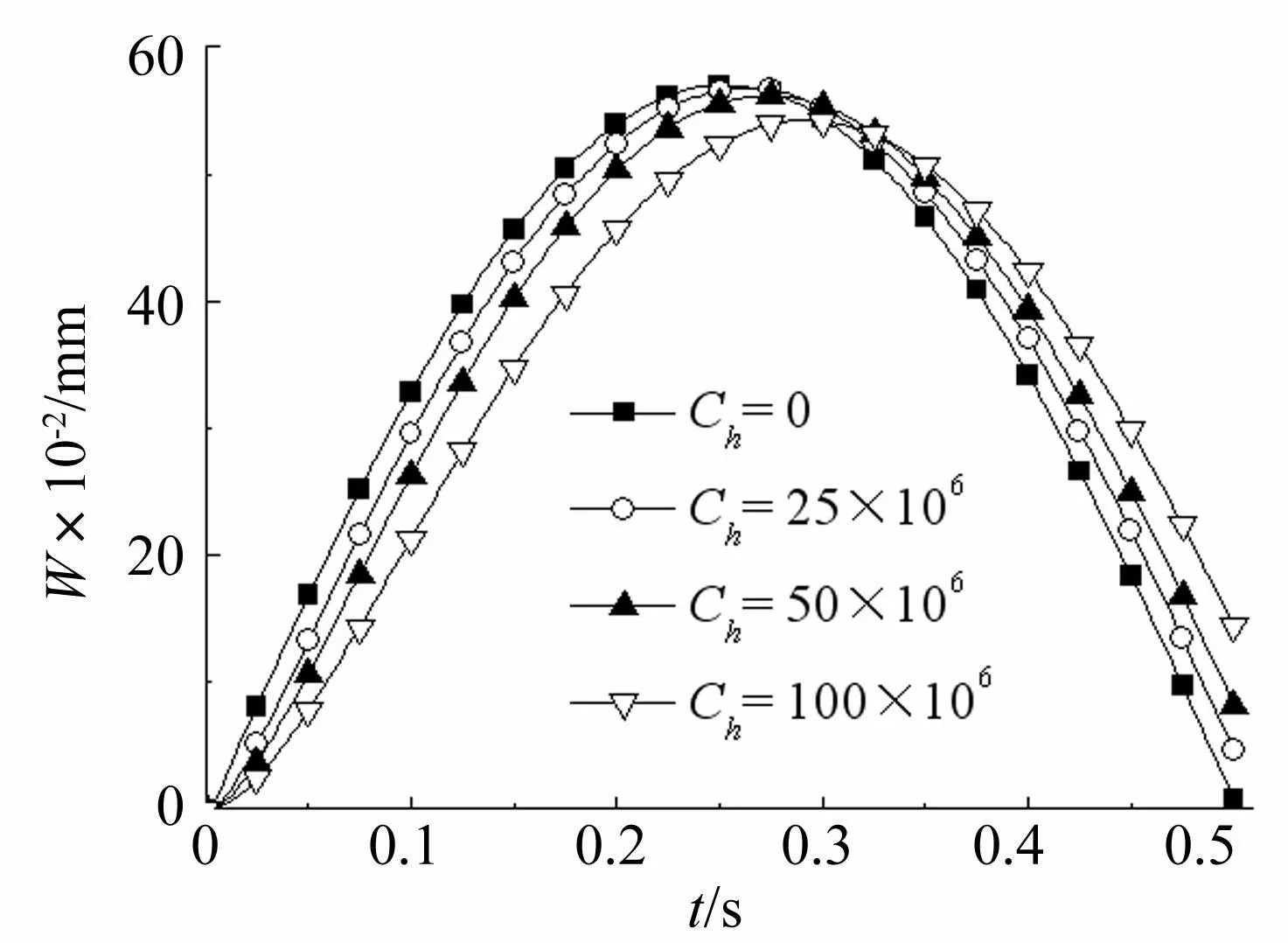
图5　不同水平阻尼系数时点2处挠度变化曲线 Fig.5 The deflection curves of point 2 under different horizontal damping coefficient values

从图4～图6中可以看出：

(1)由于阻尼力作用，考虑水平阻尼时典型点处的最大挠度要小于未考虑阻尼时的挠度。

(2)无水平阻尼时挠度最大值与载荷最大值在t=0.25 s处同时出现，而存在阻尼时板垂向位移峰值出现时刻相对于载荷峰值有一定滞后，且阻尼越大滞后时间越长。

(3)载荷加载阶段，水平阻尼越大，板挠度增长速率越小；载荷卸载时，随着阻尼的增大，垂向位移减小速率降低。

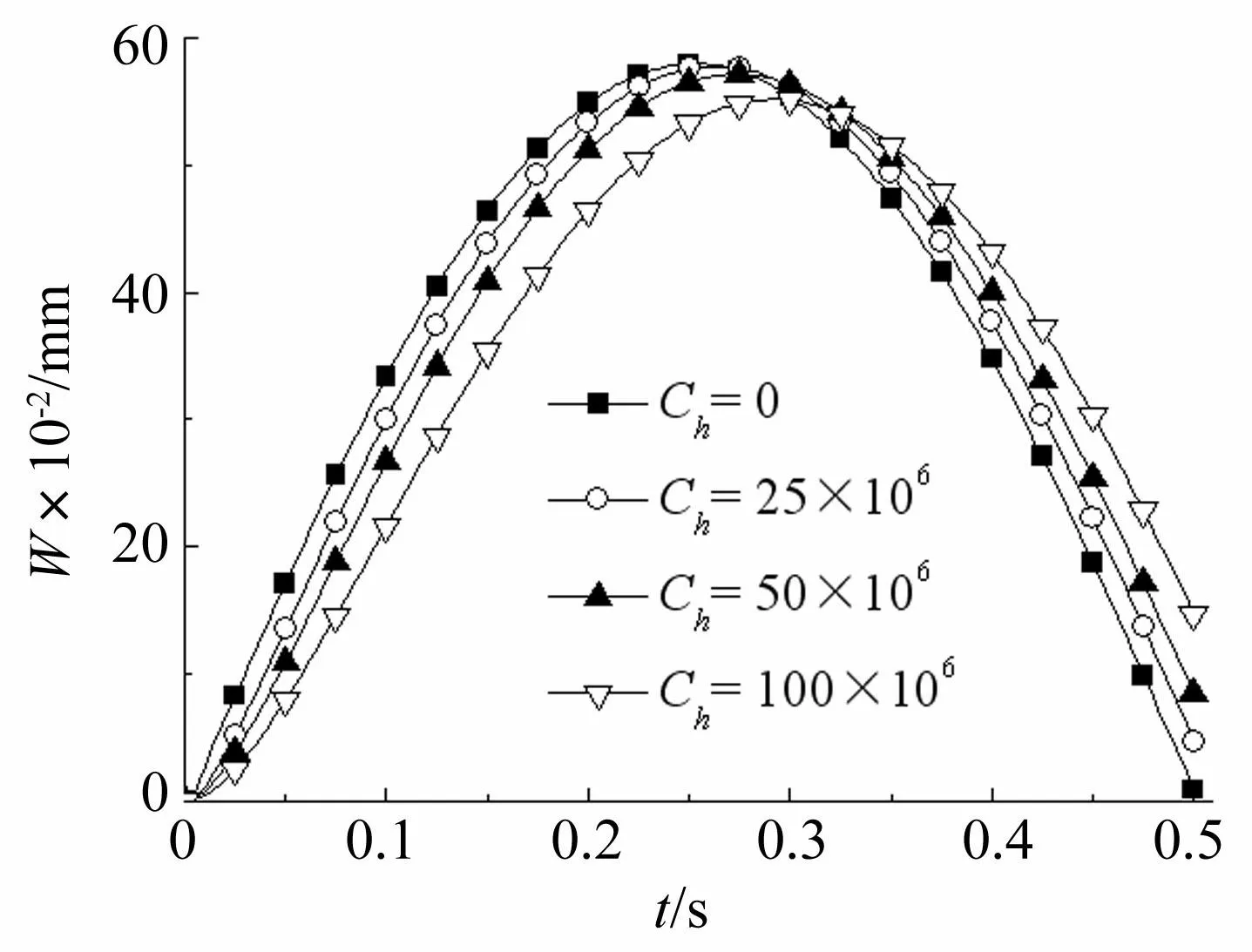
图6　不同水平阻尼系数时下点3处挠度变化曲线 Fig.6 The deflection curves of point 3 under different horizontal damping coefficient values

4.2摩擦系数λ对挠度的影响

计算时取运动方向角θ为45°，水平阻尼系数Ch为0.25×106N·s/m3。

图7为不同时刻时，摩擦系数λ与点1处板挠度的关系曲线，由图7可知，摩擦系数对点1处的垂向位移没有影响。

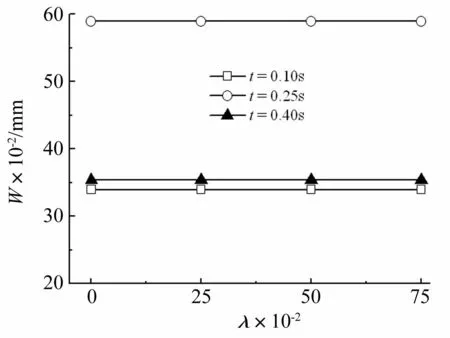
图7　摩擦系数与点1处挠度的关系 Fig.7 Relation between friction coefficient and deflection of point 1

图8、图9描述了不同摩擦系数下点2、点3处板位移变化规律，由图8～图9可知：摩擦系数愈大，点2处的位移愈小，然而点3处的扰度随着摩擦系数的增大而增大。

图10为t=0.25 s时，各摩擦系数下，不同点处的垂向位移，从图中可以看出：

(1)摩擦系数对各点处板位移的影响呈线性，对于序号为偶数的典型点处，下沉量随摩擦系数增大而增大，λ=0.75时点3的位移达到0.6 mm，而对于序号为奇数的典型点(点1除外)，摩擦系数愈大板的挠度愈小，λ=0.75时点6处板的挠度为0.4 mm。另外，与点1距离相等的两点对应的两条直线，斜率符号相反，而绝对值相等，说明摩擦系数对两点位移的影响幅度相同。

(2)从图10中可以看出，距离点1越远的点，其对应的直线越陡峭，即摩擦系数对此点位移的影响越大，点6、点7在λ=0.75时位移差值最大，达到0.13 mm。点2、点3在λ=0.75时垂向位移差值为0.05mm。

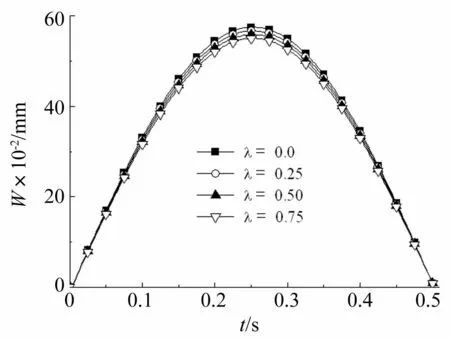
图8　不同摩擦系数时点2处挠度变化 Fig.8 The deflection curves of point 2 under different friction coefficient values

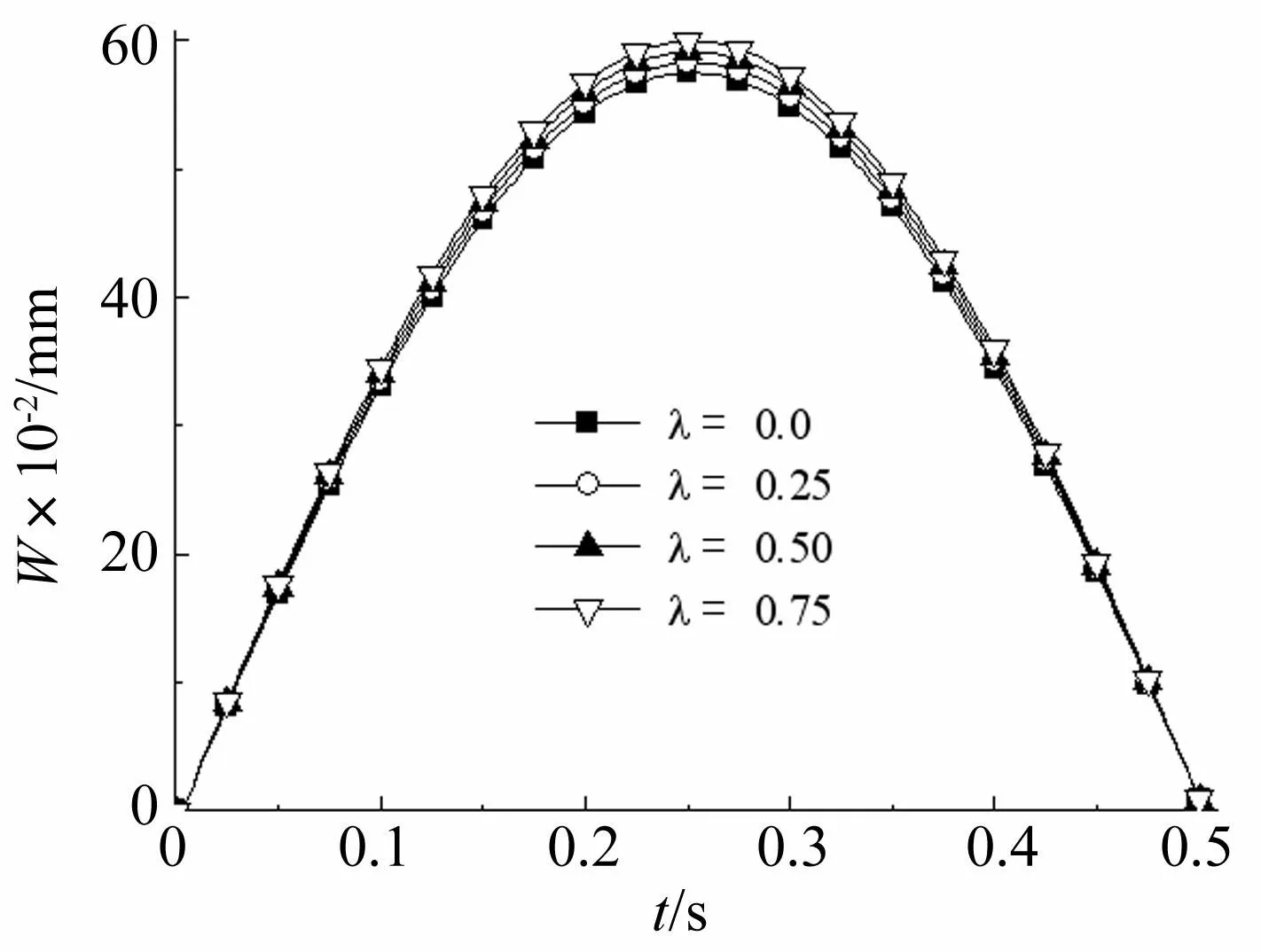
图9　不同摩擦系数时点3处挠度变化 Fig.9 The deflection curves of point 3 under different friction coefficient values

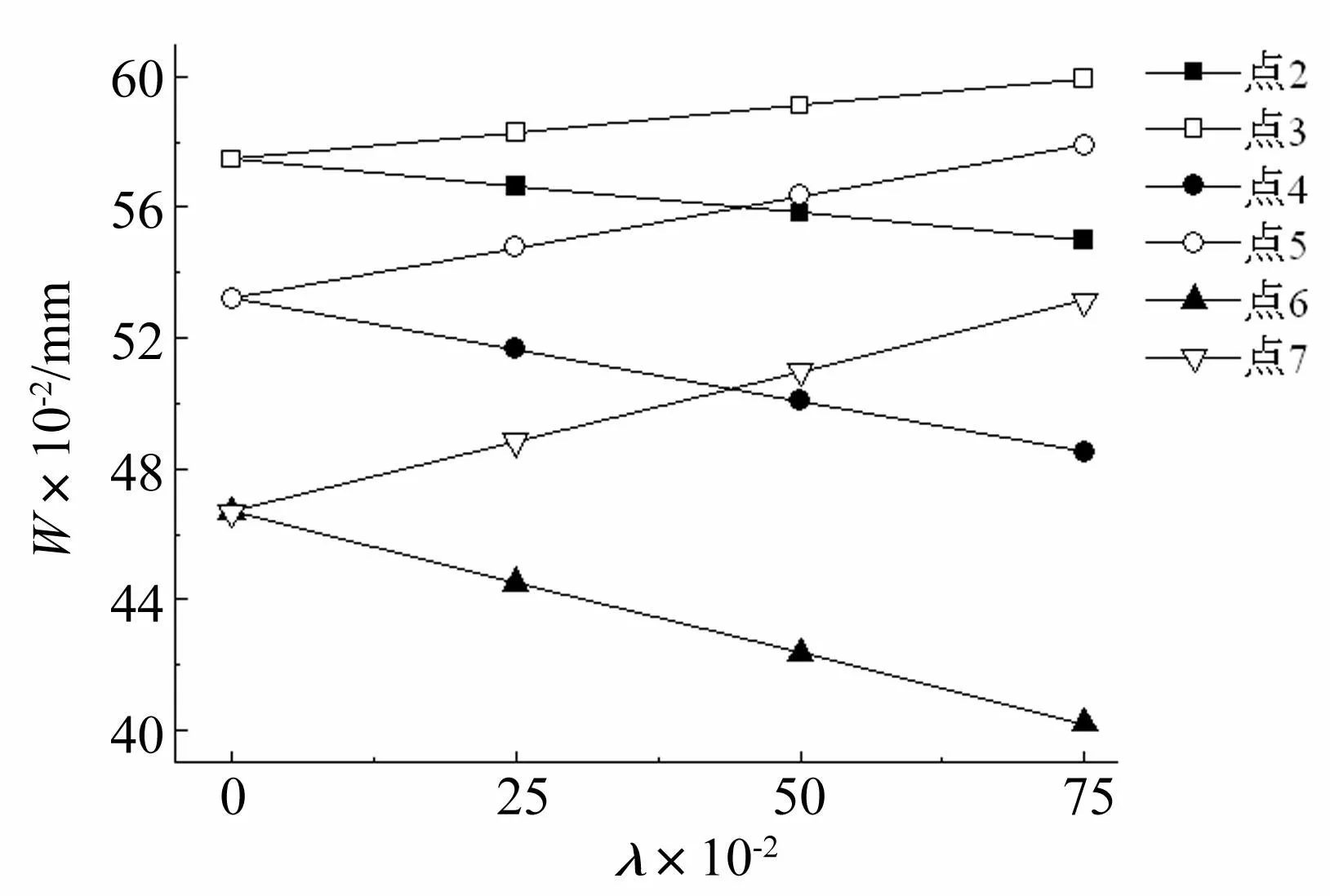
图10　t =0.25 s时摩擦系数与点2～点7处挠度的关系 Fig.10 Relation between friction coefficient and deflection of point 2～7, at t=0.25 s

4.3运动方向角θ对挠度的影响

编程计算时取摩擦系数λ=0.5，水平阻尼系数Ch=0.25×106N·s/m3。

图11为不同时刻时，方向角θ对点1处板挠度的影响，由图11可知，各方向角下点1处在同一时刻的位移相同，说明运动方向变化对点1处的挠度的影响可忽略。

图12、图13分别为不同运动方向时点2、点3处板位移变化规律。从图12～图13可得：运动方向对板挠度有较大影响，对于点2处，同一时刻垂向位移由大到小排列，对应的方向角依次为30°、15°、0°、45°，而对于点3处相应的方向角分别是45°、0°、15°、30°，由此可知运动方向对点2、点3处位移的影响并不相同。点2、点3在对称位置，若只存在垂向作用力则挠度变化规律相同，而水平力在点2处产生挤压作用，在点3处主要呈现拉伸作用，由于挤压和拉伸时板形变差别较大，因此水平力对点2、点3挠度的影响不相同，导致垂向载荷与水平载荷联合作用下对称点处挠度的变化规律出现偏差。

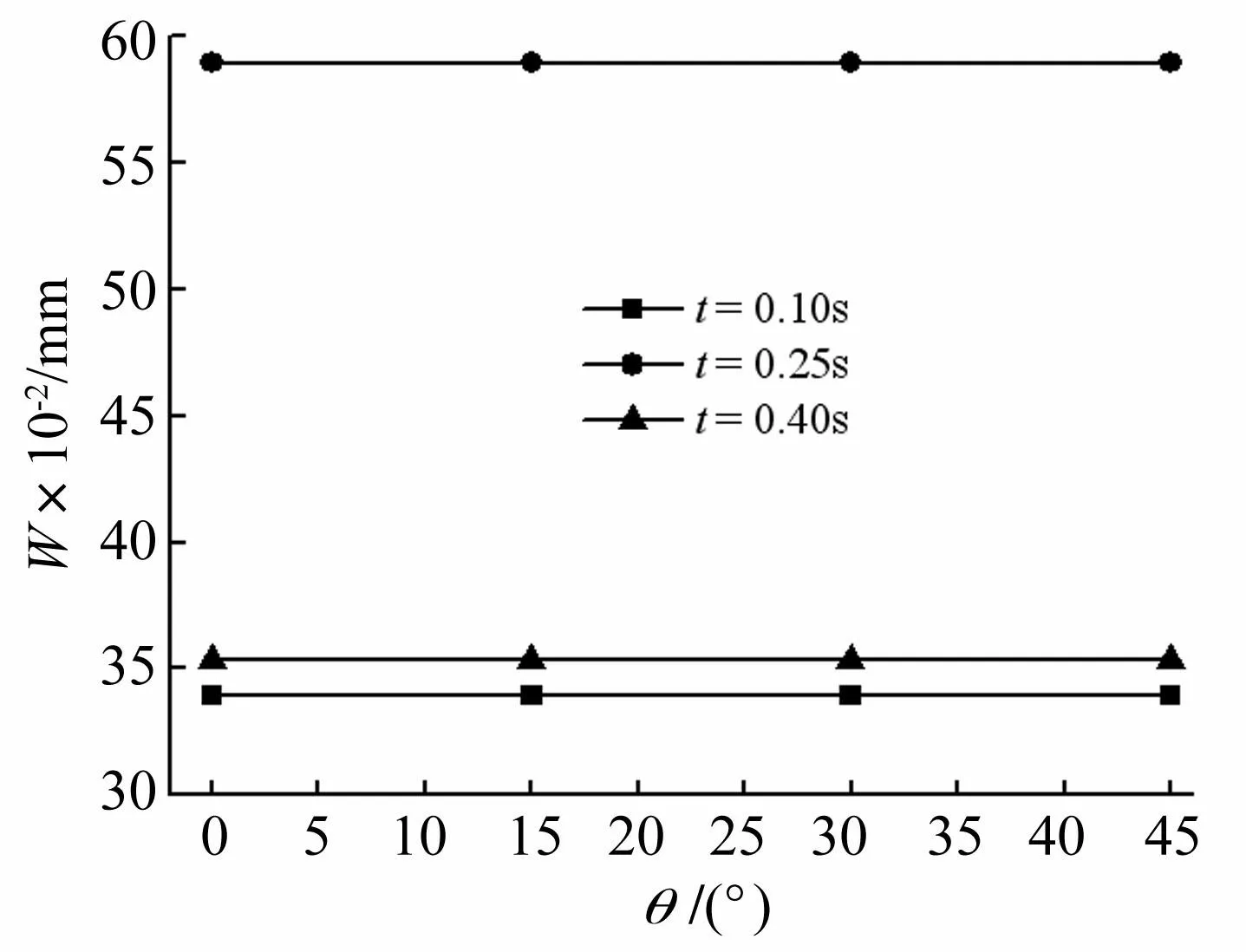
图11　运动方向与1处挠度的关系 Fig.11 Relation between motion direction and deflection of point 1

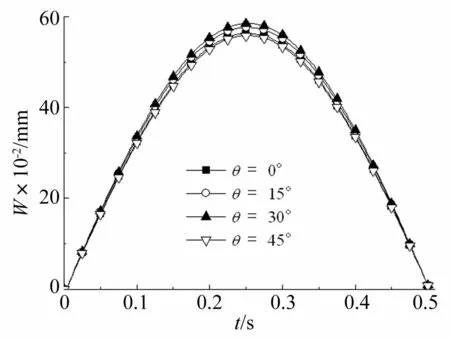
图12　不同运动方向时点2处挠度变化 Fig.12 The deflection curves of point 2 under different motion direction

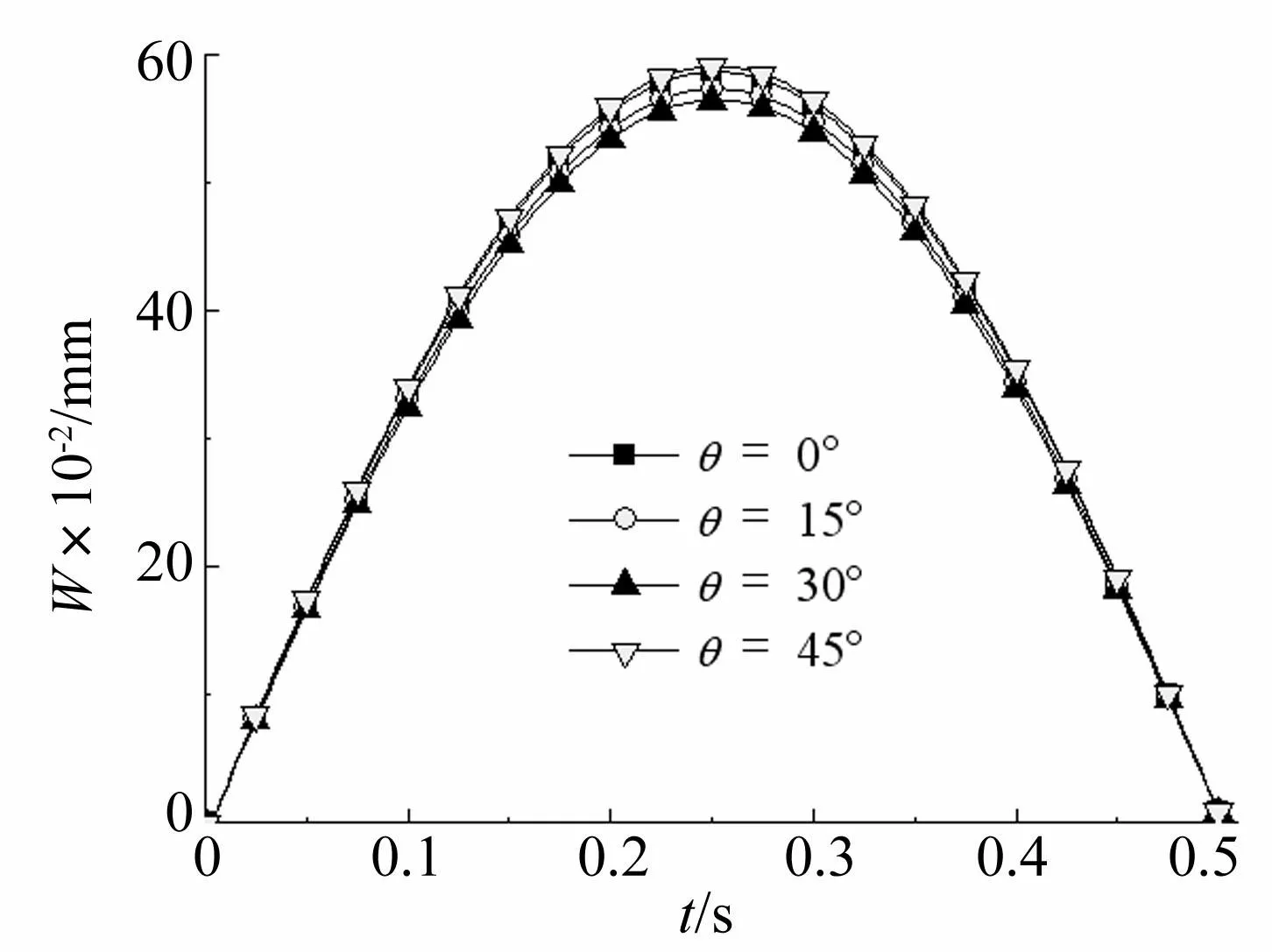
图13　不同运动方向时点3处挠度变化 Fig.13 The deflection curves of point 3 under different motion direction

图14为t=0.25 s时，各方向角下，不同点处的垂向位移，由图14可知：

(1)方向角对6个点处板挠度的影响规律近似为余弦曲线，6条曲线具有相同的周期，约为22°。序号为偶数的典型点的曲线与序号为奇数的点(点1除外)对应的曲线，两者相位差约为半个周期。

(2)与点1距离相同的两点对应的余弦曲线变化幅值相等，如点4、点5处曲线变化幅值为0.06 mm。距离点1越远的点，曲线变化幅值越大，点6、点7处曲线变化幅值为0.09 mm，点2、点3处曲线变化幅值为0.002 mm。

(3)另外，与点1距离相同的两点对应的曲线偏移量相同，点2、点3处曲线偏移量为0.575 mm，点4、点5处偏移量为0.53 mm，点6、点7处的偏移量为0.46 mm。

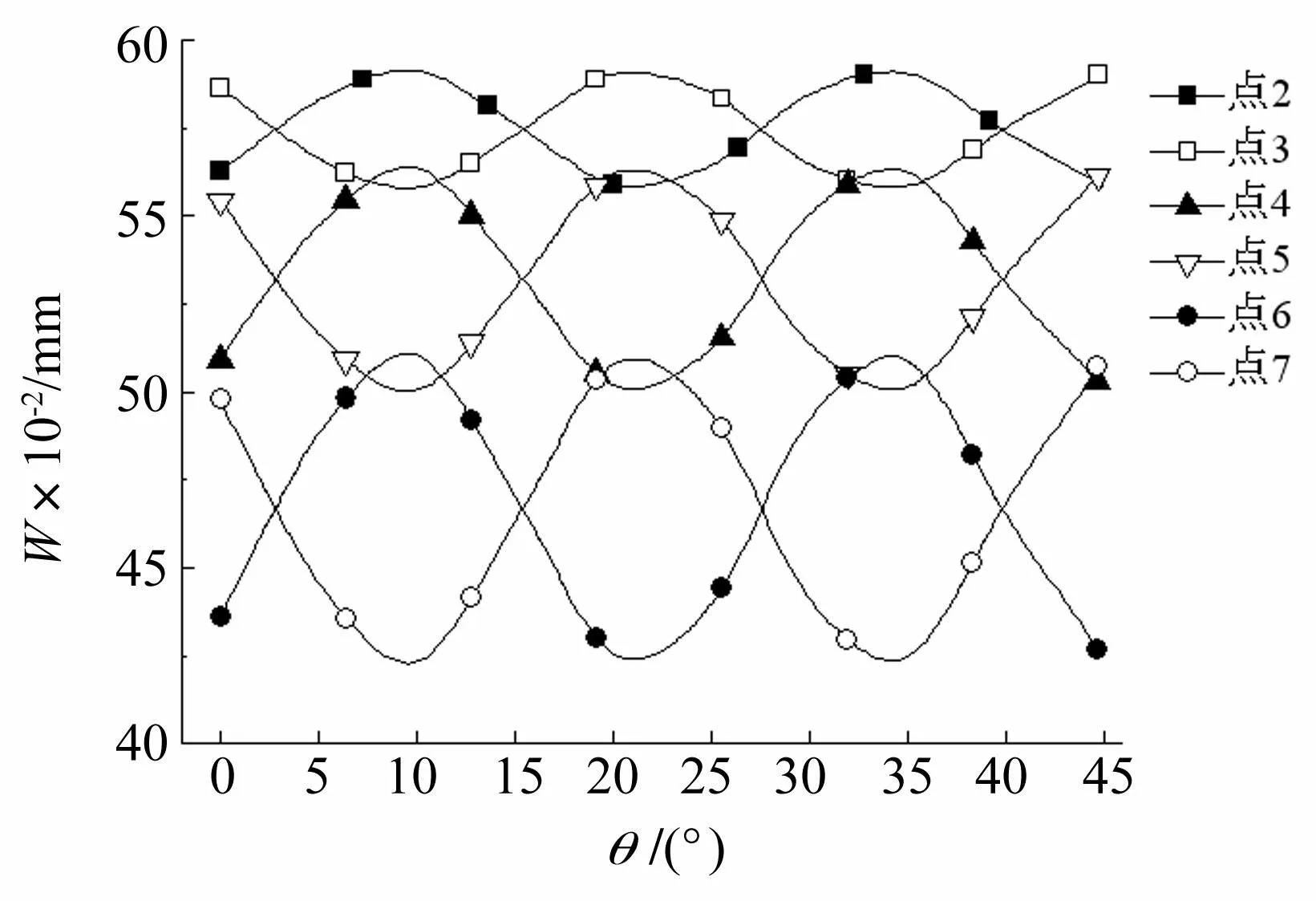
图14　t =0.25 s时运动方向与点2～点7处挠度的关系 Fig.14 Relation between motion direction and deflection of point 2～7, at t=0.25 s

5结论

提出了考虑水平阻尼的双参数地基模型，在此基础上推导了多层地基板的中性面位置表达式，给出了水平动载荷与垂向动载荷联合作用下板的运动微分方程。采用级数分解和拉氏积分变换相结合的方法，获得了圆形刚性承载板对地载荷作用下的多层地基板的挠度解析表达式，以地基上三层板为例分析了水平阻尼系数，摩擦系数及运动方向对典型点处板挠度的影响，通过分析可得出以下结论：

(1)考虑水平阻尼时板的最大挠度要小于未考虑阻尼时挠度的最大值，存在阻尼时板下沉量峰值与载荷峰值不同时出现，而是有一定滞后且阻尼越大滞后时间越长。

(2)摩擦系数对多层板位移的影响呈线性，对远离载荷作用区域圆心处点的响应影响较大。

(3)运动方向角对板挠度的影响规律近似为余弦曲线，与载荷作用面中心距离相等的两点间余弦曲线的相位差约为半个周期，并且曲线偏移量相同。方向角的变化对远离圆心处点的位移产生较大影响。

(4)摩擦系数、运动方向对载荷作用面中心处板挠度的影响可忽略。

参考文献

[1]Fryba L. Vibration of solids and structures undermoving loads[M]. London: Thomas Telford, 1999.

[2]孙璐，邓学钧. 弹性基础无限大板对移动荷载的响应[J]. 力学学报，1996，28(6)：756-760.

SUN Lu，DENG Xue-jun. General theory for steady dynamic problem of infinite plate on an elastic foundation[J]. Acta Mechanica Sinica，1996，28(6)：756-760.

[3]蒋建群，周华飞，张土乔. 移动荷载下Kelvin地基上无限大板的稳态响应[J]. 浙江大学学报(工学版)，2005，39(1)：27-32.

JIANG Jian-qun，ZHOU Hua-fei，ZHANG Tu-qiao. Steady-state response of infinite plate on Kelvin foundation subjected to moving loads[J]. Journal of Zhejiang University (Engineering Science)，2005，39(1)：27-32.

[4]姚海林，卢正，罗海宁，等. 交通载荷作用下Kelvin地基上不平整路面的动力响应分析[J]. 岩土力学, 2009, 30(4): 890-896.

YAO Hai-lin，LU Zheng，LUO Hai-ning，et al. Dynamic response of rough pavement on Kelvin foundation Subjected to traffic loads[J]. Rock and Soil Mechanics, 2009, 30(4): 890-896.

[5]卢正，姚海林，吴莎，等. 黏弹性地基板在矩形变速载荷作用下的振动分析[J]. 岩土力学, 2010, 31(11): 3613-3618.

LU Zheng, YAO Hai-lin, WU Sha, et al. Vibration analysis of a plate on viscoelastic foundation under moving rectangular loads with variable speeds[J]. Rock and Soil Mechanics, 2010, 31(11): 3613-3618.

[6]李皓玉，齐月芹，刘进. 移动荷载下黏弹性半空间体上双层板的动力响应[J]. 岩土力学，2013，34(1): 28-34.

LI Hao-yu，QI Yue-qin，LIU Jin. Dynamic responses of a two-layer plate on viscoelastic half-space foundation under moving loads[J]. Rock and Soil Mechanics，2013，34(1)：28-34.

[7]颜可珍，夏唐代，周新民. 运动荷载作用下弹性地基无限长板动力响应[J]. 浙江大学学报(工学版)，2005，39(12)：1875-1879.

YAN Ke-zhen，XIA Tang-dai，ZHOU Xin-min. Dynamic response analysis of slab on elastic foundation subjected to moving load[J]. Journal of Zhejiang University (Engineering Science)，2005，39(12)：1875-1879.

[8]颜可珍，夏唐代. 运动荷载下Kelvin地基板的动力响应分析[J]. 振动与冲击, 2008, 27(11): 163-167.

YAN Ke-zhen，XIA Tang-dai. Dynamic response of pavement on Kelvin foundation subjected to moving load[J]. Journal of Vibration and Shock, 2008, 27(11): 163-167.

[9]郑小平，王尚文. 机场道面动态响应分析[J]. 航空学报，1990，11(3)：A146-A155.

ZHENG Xiao-ping，WANG Shang-wen. Dynamic analysis of airport pavement[J] Acta Aeronautica et Astronautica Sinica，1990，11(3)：A146-A155.

[10]颜可珍，夏唐代. 黏弹性文克尔地基矩形板的稳态动力响应分析[J]. 水利学报，2005，36(9)：1077-1082.

YAN Ke-zhen，XIA Tang-Dai. Dynamic response of rectangular plate lying on viscous Winkler foundation to moving harmonic load[J]. Shuili Xuebao，2005，36(9)：1077-1082.

[11]寇磊，白云. 分数阶微分双参数黏弹性地基矩形板动力响应[J].振动与冲击, 2014, 33(8): 141-147.

KOU Lei, BAI Yun.Dynamic response of rectangular plates on two-parameter viscoelastic foundation with fractional derivatives[J].Journal of Vibration and Shock, 2014, 33(8): 141-147.

[12]Yang S P，Li S H，Lu Y J. Investigation on dynamical interaction between a heavy vehicle and road pavement[J]. Vehicle and System Dynamics，2010，48(8)：923-944.

[13]Kim S M. Influence of horizontal resistance at plate bottom on vibration of plates on elastic foundation under moving loads[J]. Engineering Structures，2004，26：519-529.

[14]郭大智，钟阳. 刚性承载板下弹性多层连续体应力和位移分析[J]. 哈尔滨建筑大学学报，1995，28(2)：17-22.

GUO Da-zhi，ZHONG Yang. Analysis of stress and displacement in elastic multi-layer continous system under rigid bearing plate[J]. Journal of Harbin University of Architecture and Engineering，1995，28(2)：17-22.

[15]颜可珍. 弹性地基上薄板的动力响应研究[D]. 杭州：浙江大学，2005.