L型耦合板结构能量传递系数特性的研究

第一作者江民圣男，硕士，1989年12月生

通信作者牛军川男，教授，硕士生导师，1974年生

L型耦合板结构能量传递系数特性的研究

江民圣1，牛军川1,2，郑建华1，隋富生3

(1.山东大学机械工程学院，济南250061; 2.山东大学高效洁净机械制造教育部重点实验室，济南250061;3.中国科学院声学研究所噪声与振动重点实验室，北京100190)

摘要：采用功率流有限元等能量方法研究高铁车厢等大型耦合结构的振动传递特性时，能量传递系数是必须首先要解决的关键问题之一。将L型耦合板结构用两耦合的半无限板代替，同时考虑了结构中传递的弯曲波、面内的纵向波和剪切波，采用行波方法对耦合边界处的波型转换进行了研究，对各传递系数进行了求解。在此基础上，讨论了入射波的入射角、板厚、入射波激励频率(20 rad/s～2e6 rad/s)等对波型变换和能量传递系数的影响规律，结果表明板厚和频率对波型变换有着重要影响，同时板厚和激励频率的增加会使面内纵向波和剪切波的作用越来越大，不可忽略。

关键词：L型耦合板；能量传递系数；激励频率；波型转换

基金项目：国家自然科学基金(51275275)；山东省优秀中青年科学家科研奖励基金(BS2010ZZ006)

收稿日期：2014-07-04修改稿收到日期：2014-08-14

中图分类号:TB123

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.022

Abstract:To study large coupled structures, such as, high speed train bodies, their energy transfer coefficients should be solved firstly when using energy methods, such as, the energy flow finite element method (EFFEM). By using two semi-infinite plates to substitute a L-shaped coupled plate and considering flexural wave, longitudinal wave and share wave in plane simultaneously, the characteristics of wave transforming were investigated and transfer coefficients were solved at the coupled boundary by using the traveling wave method. Furthermore, the effects of incident wave’s incident angle, plate thickness and incident wave excitation frequency (20rad/s～2e6rad/s) on the wave transforming and energy transfer coefficients were analyzed. The results showed that the plate thickness and the incident wave excitation frequency have important influences on the wave transforming and energy transfer coefficients; the actions of longitudinal wave and shear wave in plane become larger with increase in plate thickness and incident wave excitation frequency, they can not be neglected.

Energy transfer coefficients’ features of L-shaped coupled plates

JIANGMin-sheng1,NIUJun-chuan1,2,ZHENGJian-hua1,SUIFu-sheng3(1. School of Mechanical Engineering, Shandong University, Jinan 250061, China;2. MOE Key Laboratory of High-efficiency and Clean Mechanical Manufacture, Shandong University, Jinan 250061, China;3. The Key Laboratory of Noise and Vibration Research, Institute of Acoustics, Chinese Academic of Sciences, Beijing 100190, China)

Key words:L-shaped coupled plate; energy transfer coefficient; excitation frequency; wave transforming

诸如动车组车厢、船舰壳体等大型组合结构中大量使用了板壳等组合结构，对于这类大型耦合结构的振动分析和声学预报，相较于传统的有限元等方法，以统计能量法和功率流有限元分析等为代表的能量法存在诸多优势，获得了重要的应用[1]。

在采用能量法计算组合结构的动力学特性时，耦合界面处的能量传递及其传递系数是必须首先要解决的问题。Cremer 等[2]在著述中指出，结构中传递的弹性波在耦合处可能会产生波型转换，即结构中产生的弹性波行进至耦合处波的类型会发生改变，且存在反射及透射现象，从能量角度考虑，即入射能量一部分反射回入射板中，一部分透射到透射板。耦合处的透射和反射现象定量表现为耦合处的能量传递系数值。因此，耦合处的能量传递系数是一组极为重要的数据，也是功率流分析求解的重点之一。

针对结构中的振动能量的传递，国内外学者做了大量的工作。Cho等[3]研究了梁杆耦合结构的功率流传递问题；文献[4-8]基于功率流方法从不同角度对加筋板等耦合结构的振动进行了研究，但其中涉及的能量传递系数均采用特定算例下的数值，并未就能量传递系数进行深入讨论。对于高铁或者动车组等组合结构中最为常见耦合形式——L型耦合板结构，Park等[9]首先对L型板中面内波的传播情况进行了研究，并给出不同激励频率下的功率流密度分布情况，而忽略了对能量传递系数的讨论；Langley等[10]在考虑梁的剪切、扭转变形及转动惯量的情况下，采用动态刚度矩阵的方法对加筋板结构的功率流密度进行了讨论，但在涉及能量传递系数的分析时，仅基于特定算例下的能量传递系数进行了后续功率流有限元法的应用；李坤朋[11]基于波型转换，对结构中几种波型同时存在的情况下的功率流传递问题进行了研究，同样在获得能量传递系数之后缺少相应的讨论；赵芝梅[12]、Niu[3]等分析了激励力与被激励板的夹角对能量传递系数的影响，进而获得L型板弯曲振动功率流与面内振动功率流随激励角变化规律，但对影响能量传递系数的因素考虑不全面，而且论文中也仅考虑了弯曲波单独存在的情况。可以看出，上述学者对功率流中涉及的能量传递系数问题都做了相当积极有益的工作，但亦存在一定的不足。

本文以经典波动理论为基础，给出了L型耦合板结构的各向振动位移，根据耦合处的连续条件获得了弹性波各向振动幅值，在此基础上计算得到了耦合界面处的能量传递关系，最后讨论了不同外界激励频率和不同板厚对能量传递系数的影响，为后续进一步进行功率流有限元分析提供了理论依据。

1薄板振动方程

1.1薄板弯曲振动方程

根据文献[14]，粘滞阻尼理论的平板衰减弯曲振动方程为

(1)

w(x,y,t)=Aekfxx ekfyy ejωt

(2)

式中:kfx=kfcosθf,kfy=kfsinθf分别表示弯曲波数在x，y方向的分量，θf表示弯曲波入射角，薄板弯曲波数kf=(ρhω2/D)1/4，A为待定的幅值。

式(1)为有阻尼受迫振动的情形，现考虑简单无阻尼自由振动的情形，即η=0。如果薄板受激励而产生弯曲波入射，则将式(2)代入(1)中可求得半无限薄板的波动解为

w(x,y)=(A1e-jkfxcosθf+A3ejkfxcosθf+

(3)

式中:Ai(i=1,2,…,7)为待定的系数，指数位置正负号表示沿负方向与正方向行进的弹性波，含有虚数单位的为远场解，不含虚数单位的为近场解。

1.2薄板面内振动波动方程

根据文献[9,15]，各向同性薄板的面内自由振动方程为

(4)

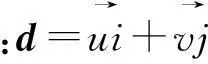
(5)

(6)

2L型耦合板能量传递系数计算

工程实际中存在大量的耦合结构，图1(a)所示的列车车厢结构模型中，在边角位置存在较多的L型板耦合结构型式。若想解决此类结构的振动问题甚至是后期对其声场进行预报，需弄清楚振动能量在耦合边界处的传递情况，这是采用功率流有限元法和统计能量法等解决声振问题必须提前解决的关键问题。图1(b)为典型的L型耦合板结构的示意图，当有某类型波由板1入射时，该型入射波行进至耦合边界处将会产生波形转换现象，如弯曲波会转换为纵向波和剪切波，同时各类型波发生反射和透射现象，即能量透射至板2和能量反射回板1，如图中箭头所示。因此，下面内容研究波型的转换规律，入射波遇耦合边界后有多少变成了其他型式的波，并进行了反射和透射，即计算能量传递系数，为接下来采用功率流有限元法评估结构中的振动能量分布打下基础。

根据文献[16]，在计算能量传递系数时，采用半无限结构近似代替有限结构所得的结果一般情况下满足精度要求，因此，本文基于该处理方法对L型耦合板的能量传递系数进行计算和分析。

图1　耦合结构模型 Fig.1 Model of coupled structure

当板1中弯曲波以入射角θf1入射时，遇耦合边界产生波型变换，根据式(3)、(5)、(7)两块板产生的x、y、z三个方向的振动位移分别为：

(7)

(8)

(9)

u2=(Al2cl2e-jxklx2-As2ss2e-jxksx2)e-jykfy2

(10)

v2=(As2cs2e-jxksx2-Al2sl2e-jxklx2)e-jykfy2

(11)

(12)

式中:Cf1,Df1,Al1,Al2,As1,As2,Af2,Bf2分别为未知的振动幅值，cosθmi=cmi,sinθmi=smi，m=f,l,s，i=1,2，θf2,θl1,θl2,θs1,θs2分别为对应波型的入射角和透射角，可由斯奈尔定律kf1sinθf1=kmisinθmi求得，Af1为已知输入幅值。

上述方程中有8个未知数，需要8个方程求解，则由耦合边界处的连续条件给出

w1(0,y)=u2(0,y)

(13)

w2(0,y)=-u1(0,y)

(14)

v1(0,y)=v2(0,y)

(15)

Qxz2(0,y)=-Nxx1(0,y)

(16)

Nxy1(0,y)=Nxy2(0,y)

(17)

Qxz1(0,y)=Nxx2(0,y)

(18)

Mxx1(0,y)=Mxx2(0,y)

(19)

(20)

式(13)～(15)为位移连续条件，式(16)、(17)和(18)分别为x、y、z轴方向上的力平衡条件，式(19)和(20)分别为弯矩平衡和转角连续条件。上述式中，Qxz,Nxx,Nxy,Mxx分别为板中的有效剪力、垂直于耦合边界的伸展力和沿耦合边界方向的剪切力和耦合边界处的弯矩，表达式形式参见文献[13]。

将式(7)～(12)代入上述8个连续条件方程可求得相应的8个未知幅值，从而求得弯曲波、纵波和剪切波在结构中传递时携带的能量为

(21)

(22)

(23)

式中，〈·〉表示时间平均。从而易得入射波遇耦合边界后各个能量透射及反射系数为

tmnij=〈Pmnij〉/〈Pmi〉

(24)

rmmii=〈Pmmii〉/〈Pmi〉

(25)

式中:Pmi为i板中的入射m波功率，Pmnij表示i板中m波引起的j中n波的功率，tmnij表示板i中m波遇耦合边界发生波形装换后透射到板j中n波所占的能量百分比，即能量透射系数，rmnii表示板i中m波遇耦合边界发生波形装换后反射回板i中n波的能量百分比，即能量反射系数，i,j=1,2为板的标号，m,n=f,l,s表示波的种类。

同样的方法，分别计算纵波、剪切波入射时耦合处的能量传递，最后可以获得三种波在耦合处的能量传递系数表达式。

3能量传递系数的讨论与分析

因为高铁车厢大多为铝型材制造，这里假设L型耦合板为均匀铝型材，各材料参数如下：E=7.1e10 Nm2,ρ=2 700 kg/m3,μ=0.3，板厚h=0.001 m，外界激励频率ω=2e6 rad/s，激励幅值取单位力Af1=1 N。通过计算获得在弯曲波入射时耦合板处的能量传递系数见图2，两曲线之间的面积就是相应能量传递系数的大小。

图2　弯曲波入射时能量传递系数 Fig.2 Transforming of power coefficient when flexural wave input

由图2可以看出，当弯曲波入射时，入射角范围为0°～90°，0°为正入射，90°为平行于耦合边入射，入射角由0°到90°变化的过程中，能量传递系数随弯曲波入射角的变化而变化，变化规律与文献[2]是一致的，验证了本文采取的计算方法的正确性。

另外，由斯奈尔定律知，当sinθf=kl/kf=0.3和sinθf=ks/kf=0.5存在能量传递系数的突变，由低到高分别对应纵向波和剪切波的临界角。当入射角小于纵向波的临界角时，存在弯曲波到纵向波和剪切波的全转换；当入射角在纵向波临界角到剪切波临界角范围内，则只存在弯曲波到剪切波的波型转换；当入射角大于剪切波的临界角时，则不存在波型转换，只有反射和透射的弯曲波。

3.1板厚h对能量传递系数的影响

基于上述对能量传递系数的计算结果，首先讨论板厚对L型耦合板耦合处能量传递系数的影响。板厚的变化范围为0.001 m～0.1 m，仍保证h1=h2。

图3为板1内入射弯曲波遇耦合边界后反射回板1的弯曲波的能量反射系数随入射角和板厚的变化规律。从图中可以看出，当板厚较小时(如h=0.001 mm)，则能量反射系数变化较为复杂，总体上随着弯曲波入射角的增大而增大，并且存在突变峰值，该位置对应两种波型的临界角，超过临界角后，不再存在波型转换现象；当板厚较大时，能量反射系数随入射角变化较为平缓，无峰值，同时可以看出，能量反射系数随着板厚的增大总体也呈现增大趋势。

图4为板1中入射弯曲波遇耦合边界后产生的反射回板1的纵波能量反射系数随入射角及板厚的变化规律。可以看出，在板厚较小时，超过临界角后存在无纵波反射的情况，表现为图中部分曲线能量传递系数值为0；随着板厚h继续增大，无论入射角度如何变化，都存在反射纵波，且越接近正入射能量反射系数越大，但与图3中的弯曲波能量反射系数相比要小的多，正入射时最大值仅为0.08。

图5为板1中入射弯曲波遇耦合边界后产生的反射回板1的剪切波能量反射系数随入射角及板厚的变化规律。同样可以看出在超过临界角后，无剪切波反射，当板厚由h=0.1 mm逐渐减小时，临界角增大，仍存在剪切波的反射，当厚度小于约0.07 mm时，无论入射角度如何已经基本上没有剪切波存在，也就是说薄板情况下，剪切波完全可以忽略。

图6为板1中入射弯曲波遇耦合边界后产生的透射到板2的弯曲波的能量透射系数随入射角及板厚的变化规律。结合图2可以知道，板厚较小时，能量透射系数变化比较复杂；板厚增大时，无论弯曲波以何种角度入射，皆存在弯曲波的透射现象，且越接近正入射，透射的波的能量越大。

图7为板1中入射弯曲波遇耦合边界后产生的透射到板2的纵波的能量透射系数随入射角及板厚的变化规律。结合图2可知，薄板时，若入射角大于临界角，则没有透射的纵波，实际上，这时如图4所示也没有反射的纵波，也就是超过临界角时，不再有弯曲波到纵向波的波型转换；对于厚板，纵波能量透射系数基本不随入射角变化而变化。

图8为板1中入射弯曲波遇耦合边界后产生的透射到板2的剪切波的能量透射系数随入射角及板厚的变化规律。结合图2可以看出，薄板时，超过剪切波的临界角时，不再有透射的剪切波，对于厚板，则不存在这种现象；另外，板厚越小，入射角度越大，透射到板2中的剪切波就越多。

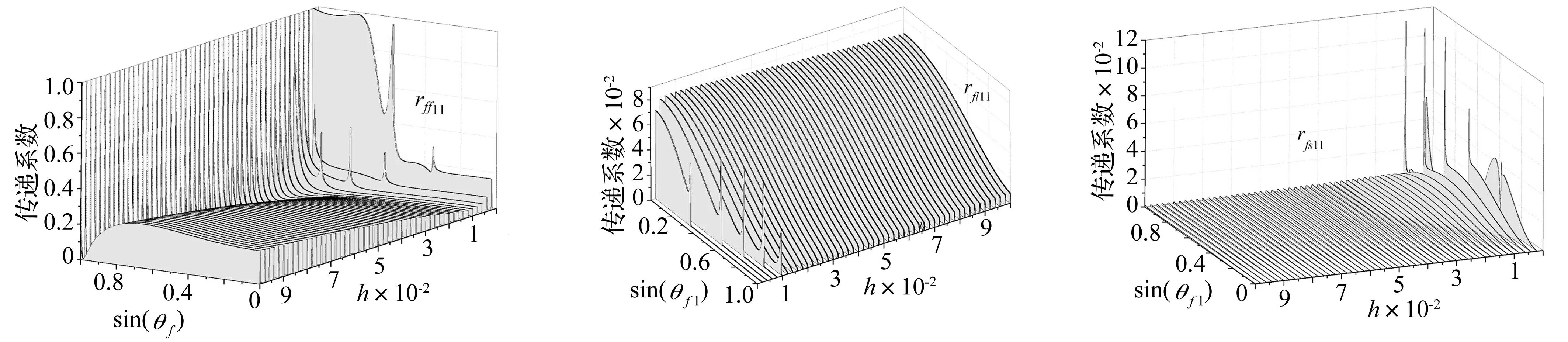
图3 板厚h对rff11的影响Fig.3Thethickness(h)influenceonrff11图4 板厚h对rfl11的影响Fig.4Thethickness(h)influenceonrfl11图5 板厚h对rfs11的影响Fig.5Thethickness(h)influenceonrfs11

图6 板厚h对tff12的影响Figure.6Thethickness(h)influenceontff12图7 板厚h对tfl12的影响Fig.7Thethickness(h)influenceontfl12图8 板厚h对tfs12的影响Fig.8Thethickness(h)influenceontfs12

3.2激励频率ω对能量传递系数的影响

接下来分析在板厚确定(h=0.001 m)的情况下，激励频率变化(ω=20～2e6 rad/s)对能量传递系数的影响，同样以弯曲波入射为例，可以得到如图9～图14的分析结果。

图9～图11分别为板1内入射弯曲波遇耦合边界后反射回板1的弯曲波、纵波和剪切波的能量反射系数随入射角和激励频率的变化规律。

从图9看出，两个峰值对应面内波的两个临界角，频率的增大使两个临界角增大；而当弯曲波入射角大于该临界角时，随着外界激励频率的增大，能量反射系数也随之增大。

由图10可知，当入射角小于纵向波临界角时,纵波能量反射系数将随着激励频率的增大而增大，即弯曲波向纵波的波型转换在增强，但从图中可以看出能量反射系数很小，最大值约为0.075；当入射波超过这一临界角，则不再发生弯曲波向纵波的波型转换。

从图11可知，反射剪切波与纵波有同样的变化规律。当入射波小于剪切波临界角时，存在弯曲波向剪切波的波形转换，且随着激励频率的增大转换的强度在增加，从图中同样可以看出，能量反射系数也很小，最大值不到0.1；弯曲波入射角大于剪切波临界角时，则不再发生弯曲波到剪切波的波形装换，则能量反射系数为0。

综合图10～图11可知，随着激励频率的增大，面内波的反射能量也在随之增加。

图12～图14分别为板1内入射弯曲波遇耦合边界后透射到板2的弯曲波、纵波和剪切波的能量反射系数随入射角和激励频率的变化规律。

图12表明随着外界激励频率的增大，峰值对应的弯曲波入射角逐渐变小，总体上发生透射的弯曲波比重总体在减小。

从图13可以看出，随着激励频率的增大，板内透射的纵波切波能量也在增加；同样，当入射波的入射角大于纵波临界角时，不再有弯曲波到透射纵波的波型转换；另外，面内纵向波的临界角随频率的增加而缓慢增加。

根据图14可知，在剪切波临界角范围内，透射的剪切波随着激励频率的增大而增大，当超出这一临界角，则不再发生弯曲波到透射剪切波的波型转换。

图9 激励频率变化对rff11的影响Fig.9Variationofrff11withexcitationfrequencyandtheincidentangle图10 激励频率变化对rfl11的影响Fig.10Variationofrfl11withexcitationfrequencyandtheincidentangle图11 激励频率变化对rfs11的影响Fig.11Variationofrfs11withexcitationfrequencyandtheincidentangle

图12 激励频率变化对tff12的影响Fig.12Variationoftff12withexcitationfrequencyandtheincidentangle图13 激励频率变化对tfl12的影响Fig.13Variationoftfl12withexcitationfrequencyandtheincidentangle图14 激励频率变化对tfs12的影响Fig.14Variationoftfs12withexcitationfrequencyandtheincidentangle

综合图13～图14可知，随着外界激励频率的增大，面内透射波的能量也随之增加，所以对于高频振动，面内剪切波的影响应给予充分的重视。

4结论

采用能量方法研究大型耦合结构的振动传递特性时，能量传递系数是必须要用到的关键参数。针对耦合结构中最常见的L型耦合板，文章同时考虑了结构中传递的弯曲波、面内的纵向波和剪切波，采用行波方法对最常见的L型耦合结构的能量传递系数进行了求解。

通过仿真计算，讨论了弯曲波入射角、板厚和激励频率对波型转换和能量传递系数的影响，结果表明：

(1)在激励频率一定的情况下，对于薄板，只有入射角小于相应的临界角，才会有波形转换现象，随着板厚的增加，入射弯曲波将发生波型的全转换现象，且透射能量占主导地位；

(2)对于大型结构的薄板耦合，在板厚一定的情况下，随着外界激励频率的增大，则相应的临界角缓慢增大，而透射弯曲波的能量占比将减小，面内波的比重在则逐渐增大，且透射的面内波能量占主要成分;

(3)对于厚板和高频工况，面内纵向波和剪切波的作用越来越大，因此，在采用功率流有限元法等能量方法研究耦合结构高频振动时，必须考虑波型转换波现象，计入面内波的影响，否则将会导致分析结果不准确甚至错误。

参考文献

[1]宋孔杰, 张蔚波, 牛军川. 功率流理论在柔性振动控制技术中的应用于发展[J]. 机械工程学报, 2003, 39(9): 23-28.

SONG Kong-jie, ZHANG Wei-bo, NIU Jun-chuan. Application and development of power flow theories in the field of the vibration control for flexible systems[J]. Chinese Journal of Mechanical Engineering, 2003, 39(9): 23-28.

[2]Cremer L, Heckl M, Ungar E E. Structure-borne sound, second edition [M]. Springer-Verlag, 1988.

[3]Cho P E. Bernhand R J. Coupling of continuous beam models[M]. Proceedings of Inter-noise, Toronto, 1992: 487-492.

[4]Mace B R. Power flow between two coupled beams [J]. Journal of Sound and Vibration, 1992, 159(2): 305-325.

[5]李天匀, 张维衡, 张小铭. L型加筋板结构的导纳功率流研究[J]. 振动工程学报, 1997, 10(1): 112-117.

LI Tian-yun, ZHANG Wei-heng, ZHANG Xiao-ming.Mobility power flow analysis on a L-shaped stiffened plate[J]. Journal of Vibration Engineering, 1997, 10(1): 112-117.

[6]仪垂杰, 连小珉. 梁-阶梯板耦合结构的功率流[J]. 清华大学学报:自然科学版, 1996, 36(3): 96-100.

YI Chui-jie, LIAN Xiao-min. Power flow in assemblies of beam-flat plate with stepped discontinuity[J]. Journal of Tsinghua University:Sci & Tech, 1996, 36(3): 96-100.

[7]王敏庆, 周庆余. 板受力激励下加筋板结构振动功率流[J]. 声学学报, 1997, 22(4): 323-328.

WANG Min-qing, ZHOU Qing-yu.Vibrational power flow in infinite stiffened-plates with force excitation applied on plate[J]. Acta Acustica, 1997, 22(4): 323-328.

[8]王彦琴, 盛美萍, 孙进才. 变截面梁-板耦合结构的功率流[J]. 振动与冲击, 2005, 24(2): 33-36.

WANG Yan-qin, SHENG Mei-ping, SUN Jin-cai, et al.Study on power flow in non-uniform beam-plate assembly[J]. Journal of Vibration and Shock, 2005, 24(2): 33-36.

[9]Park D H, Hong S Y. Power flow models and analysis of in-plane waves in finite coupled thin plates [J]. Journal of Sound and Vibration, 2001, 244(4): 651-668.

[10]Langley R S, HeronK H. Elastic wave transmission through plate/beam junctions [J]. Journal of Sound and Vibration, 1990, 143(2): 241-253.

[11]李坤朋. 基于能量有限元法的板耦合结构振动特性分析[C]. 济南: 山东大学, 2013.

[12]赵芝梅, 盛美萍. 激励特性对L型板振动功率流的影响[J]. 兵工学报, 2013, 34(8): 986-993.

ZHAO Zhi-mei, SHENG Mei-ping.Effect of driving force characteristics on the power flow of L-shaped plate[J]. Acta Armamentatii, 2013, 34(8): 986-993.

[13]Niu J C, Li K P. Energy flow finite element analysis of L-shaped plate Including three types of waves[J]. Applied Mechanics and Materials, 2013, 353-356: 3365-3368 (EI)

[14]Bouthier O M, Bernhard R J. Simple models of energetic of transversely vibrating plates [J]. Journal of Sound and Vibration, 1995, 182(1): 149-164.

[15]Miklowitz J. The theory of Elastic waves and waveguides[M]. Amsterdam: North-Holland, 1978.

[16]Cho P E. Energy flow analysis of coupled structures [D]. PhD Thesis, Purdue University, USA, 1993.