葡萄酒的评价

夏克强

摘 要 本文建立了葡萄酒评价的符号秩检验和灰色聚类分析模型。为了得到每组评酒员对各个酒样品的客观评价分数，对每组评酒员对酒样品的评价分数做平均值，得到该酒样品总体评分，然后将两组评酒员的评价结果作差，得到的差值作成对数据的符号秩检验，最后采用SAS软件计算出符号秩检验中 = 0.0085，小于显著性水平 = 0.05，故不接受原假设，即两组评酒员的评价结果有显著性差异；对于置信度的问题，我们对各个评酒员对酒样品的评分作方差分析，分别计算出第一、二组评分结果的方差和分别为1409.3、821.1，易知第一组的方差和远大于第二组，所以第二组的评价结果更稳定，也更可信。将第二组评酒员对红葡萄酒的评价结果进行等级分类，再采用灰色聚类分析的方法对红葡萄的样品进行分级，结合其酿造出的葡萄酒的品质，即该葡萄样本所酿造的葡萄酒的级别，来确定该葡萄酒的级别。

关键词 葡萄酒评价 符号秩检验 灰色聚类分析

中图分类号：TS262.6 文献标识码：A DOI：10.16400/j.cnki.kjdkz.2015.12.066

Abstract This paper established a signed rank test and gray clustering model wine evaluation. In order to get each group wine-tasting each wine sample an objective evaluation score for each group of wine-tasting wine samples for the evaluation scores do mean to give the wine sample overall score， and then the evaluation results of the two groups for wine-tasting poor， made the difference to get the data signed rank test， and finally the use of SAS software to calculate the signed-rank test = 0.0085， and less than the significance level = 0.05， it does not accept the original hypothesis that the evaluation results of two wine-tasting are significant differences； For the question of confidence， and we each wine-tasting wine samples ratings for variance analysis， were calculated first and second set of score results of variance and were 1409.3，821.1， easy to know and much larger than the first group variance The second group， so the evaluation results of the second group is more stable and more reliable. The second group of wine-tasting red wine for the evaluation of the results will be classification， then using gray cluster analysis of the samples were graded red grapes， combined with its wine is quality， both in the grape samples wines level， to determine the level of the wine.

Key words wine evaluation； signed rank test； grey cluster analysis

1 问题重述

1.1 研究课题背景

针对主观性评价问题和多目标问题，由于其繁琐性和主观性，对我们来说，很难透过现象看本质，虽然层次分析法在PHP中可以通过得分函数构成。但就其缺点而言，我们认为对这类模糊性问题采取多目标分层次的解决方式，而利用统计分析里的方差分析和灰色关联度分析能够合理处理此类问题。对于未来预测性和多目标问题可以得到很好的预见性效果。同时也为多领域多目标问题中提供一个较好的模型。

本文的模型也可适当地对研究人事、招聘及高校评选的处理方法有所帮助和提高。

2 问题分析

因为两组品酒员对酒样的评分是成对比较，且对评分并不要求成对数据之差服从正态分布，只要求对称分布，故我们采用统计学中Wilcoxon符号秩检验来解释两组品酒员对葡萄酒的评价有无显著性差异。

假设两组品酒员对葡萄酒的评价有显著性差异，就需要确定哪组品酒员的评价更可信，为此对品酒员评价数据做置信度分析——方差分析，由于葡萄酒评价数据无法进行复测，就要利用matlab软件的信度分析功能，分别对第一组和第二.组的评分进行可信度分析，最后通过图形直观的反映结果。

3 模型建立

3.1 符号秩检验模型的建立

将两组评酒员分别看作两个整体、，对每个红葡萄酒样品进行评价，对每个红葡萄酒样品的评价结果通过组内每一位品酒员的评分的均值 = 来刻画，同样对每个红葡萄酒样品的评价结果用均值 = 来刻画，从而得到两组评酒员对每种样品酒的评价结果，建立两组评酒员对红葡萄酒的评价。

对同一酒样品得到一对数据。可知两对数据之间差异是由各种因素，如葡萄酒的外观、香气、口感、材料成分等因素引起的。由于各酒样品的特性有广泛的差异，就不能将第一组评酒员对27 种红葡萄酒的评价结果看成是同分布随机变量的观测值。因而表1中第一行不能看成是一个样本的样本值，同样第二组的数据也不能看成是同一个样本的样本值，而同一对中两个数据是同分布随机变量的观测值，他们的差异是由于两组品酒员的水平引起的。为鉴定他们的评价结果有无显著性差异，可使用基于成对数据的逐对比较法。以红葡萄酒样品为例，有27对相互独立的评价结果：（，），（，），…，（，），令 = ， = ，…， = ，则，，…，相互独立，所以我们对，，…，进行单因素的符号秩检验。

再对和中的元素分别求和得到方差和，用方差和对比得到对于同一批红葡萄酒两组的不同评价水平。方差和小的稳定性好，相对来说比另一组的评价结果更可信。

3.3 灰色聚类分析模型的建立

在附件2中我们可以得到，对于红葡萄酒，有对应的30个一级指标，为了使结果更具有客观性，我们将葡萄酒的质量也作为一级指标。对于这31个一级指标，其中多酚氧化酶活力、褐变度、总酚、固酸比、出汁率这5个指标与葡萄酒质量呈负相关，其余26个指标都与葡萄酒质量呈正相关。

4 模型求解

4.1 符号秩检验模型的求解

对于该模型，我们首先作出同一酒样品分别由两组品酒员，得到的评价结果之差，列于表1的第三行。根据建立模型的需要假设

： = 0，：≠0

我们取 = 0.05，并采用SAS软件编程处理，具体程序见附录程序1。

在SAS中运行的结果如图1：

结果显示符号秩检验对应的P为0.0085，小于显著性水平0.05，故不接受原假设，即认为这两组品酒员分别对红葡萄酒的评分有显著性差异。

4.2 方差分析模型的求解

运用MATLAB软件编程求解，得到，。

对于红葡萄酒而言：元素的和为1409.3，元素的和为821.1。由此可以得出，第一组的方差和远远大于第二组。

4.3 灰色聚类分析模型的求

我们先对红葡萄酒质量的评价结果按评分从小到大排列得到表1：

根据等级分级标准：高级葡萄酒：9、23、20；上等葡萄酒：3、17、2、26、14、19、5、21、4、24、27、22；中等葡萄酒：16、10、13、1、12、25、6、15、7、8；下等葡萄酒：18、11。

对于每类葡萄中的元素，结合该葡萄样本所酿造的葡萄酒的级别，来确定该葡萄的级别。然后再根据每类葡萄中葡萄样本级别的比例来确定该类葡萄的级别。对应葡萄酒的等级分类，我们根据葡萄的聚类分析也将葡萄分成高级、上级、中级、下级。

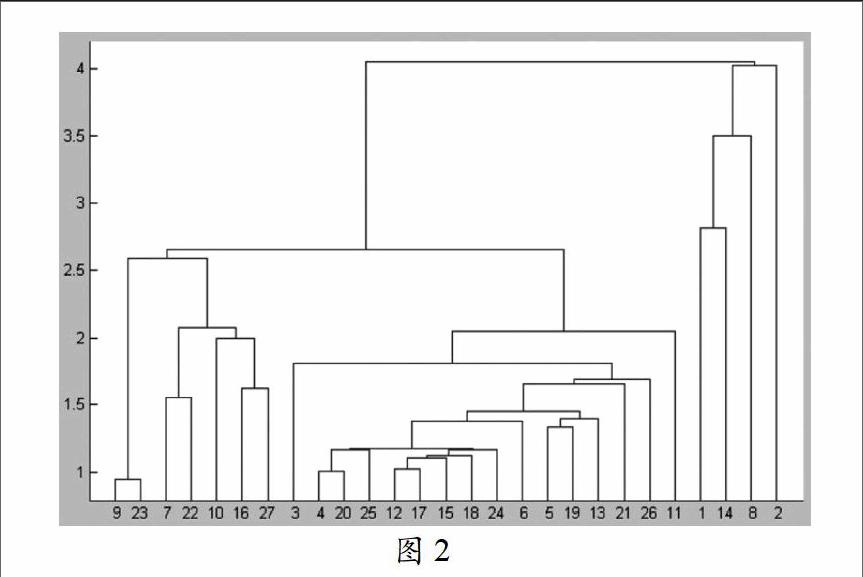
红葡萄的分类结果：高级红葡萄：9、23、4、20；上级红葡萄：3、17、12、15、18、24、5、19、13、21、2、26；中级红葡萄：10、16、27、1、14、25、6、7、22、8；下级红葡萄：11。

参考文献

[1] 韩中庚.数学建模方法及其应用.高等教育出版社，2005.

[2] 姜启源等.数学建模.高等教育出版社，2011.