EXCEL单元格三种地址表示方法与实例

徐保华　尹利勇　郭建

摘 要 本文系统地介绍了EXCEL单元格的三种地址表示方法，这是深入学习EXCEL和拓展EXCEL知识的基础，还结合具体实例阐述了三种地址表示方法的特点和如何应用等内容。

关键词 EXCEL单元格 地址表示方法 实例

中图分类号：TP317.3 文献标识码：A DOI：10.16400/j.cnki.kjdkz.2015.12.012

Abstract This paper systematically introduces three EXCEL cell address representation， which is the in-depth study EXCEL EXCEL and expand knowledge base， but also with specific examples illustrate three address representation features and how to use and so on.

Key words EXCEL； address representation methods； example

单元格地址表示方法是为Excel智能运算服务的，这也是Excel不同于计算器和其他电子表格的地方。使用普通计算器时，需针对不同的数据重复进行计算，即浪费时间又不能发现数据的变化规律。而使用Excel进行计算时，对于相同的运算，不需要重复进行，只要针对不同的应用问题写出对应的自变量的地址，就可以通过“拷贝”公式的功能得出其他单元格中的结果。所以说，在EXCEL中对公式或函数的“拷贝”是进行智能运算的助手。为此，先综述一下各种“拷贝”方法。

在EXCEL中“拷贝”操作可以使用通用的拷贝方法，如快捷键方法：Ctrl+C 再Ctrl+V；或人们习惯用的拷贝与粘贴两个图标方法以及右键快捷菜单方法。上述这些“拷贝”方法都需借助剪贴板来进行。若按Ctrl+左键拖被选内容，则不需要将拷贝信息事先注入剪贴板，这也是常用的一种拷贝方法。这些通用的拷贝方法对于EXCEL的计算不很方便，当待拷贝的公式单元格较多时，既浪费时间还容易出错。为此，EXCEL给出一种特殊的拷贝方法：拖公式单元格右下角的（细十字）“填充柄”进行公式或函数的拷贝操作。需要注意的是：这种拷贝方法仅限于相邻单元间的拷贝，而在EXCEL中我们最需要的恰恰就是相邻单元格间的快速拷贝方法。

为了能正确地计算出数据库类型表格中的公式或函数结果，自变量所在的单元格必须使用“相对地址”表示，即用“列标+行号”来表示。如A2表示第一列第二行中的数据，对于一个自变量区域，不必一个一个地写出来，可以用左上角和右下角单元格地址简捷地表示，两者之间用英文的冒号隔开，如A3：D6就表示一个含有16个单元格的矩形区域，在进行公式运算时特别方便。

用“相对地址”表示自变量单元格时的特点是：自变量单元格地址与（因变量）公式单元格的地址在空间布局上看是不变的，不会因为“拷贝”操作而改变。例如，某个单元格中的公式是计算左面3个单元格数据之和，则不论将该公式“拷贝”到哪个单元格中，结果始终是左面3个单元格数据之和。这就是我们在做成绩统计时，只要计算出第一个学生的总成绩，再向下拖动“填充柄”进行拷贝，就会得到其他同学的总成绩的原理。也就是说，用相对地址表示自变量时，自变量的地址始终是跟随因变量变化而变化的，并计算出其他单元中的结果。单元格的相对地址表示方法普遍适用于成绩表、设备表、工资表等数据库形式的表格统计与计算。

EXCEL单元格地址的第二种表示方法是：绝对地址表示法。所谓“绝对”就是永恒不变的意思，即自变量单元格不会跟随因变量变化而变化，形象地说，单元格地址被锁住了。在数据库计算和其他表格制作时均有应用。

绝对地址表示方法是：在自变量单元格的列标和行号前均加$号。如：一个单元格的绝对表示是$B$4，一个区域的绝对地址表示是$B$4：$D$7。

我们在制作数据表格时，有时需要对自变量进行筛选、比较，例如：在对一个班级学生成绩进行排位时，需逐个比较每名学生成绩在班级所有同学成绩中的位置。其中，单个学生的成绩是变化的，须用相对地址表示，而所有学生成绩的单元格区域必须是不变的，不能因为学生变化而改变，在Excel中这种不变的自变量或区域采用“绝对地址表示”。在对公式或函数单元格“拷贝”时，用“绝对地址表示”的区域始终保持不变，与“拷贝”无关。

在前面提到的学生成绩排位问题中，成绩对比区域必须用“绝对地址”表示，与此类似的应用问题很多。虽然我们可以用“排序”图标来进行，但这种排序方法会破坏原有表格行的位置，这恰恰是我们最不希望看到的。为此，用Excel 的排位函数Rank可以实现在不改变原有数据库记录次序的前提下，又能添加一个“排位”字段的功能。应用时的格式为：Rank（变量，变量区域，0或1）。其中，“变量”用相对地址表示，是跟随因变量变化的，第二个参数“变量区域”是变量大小比较的区域，在排序的过程中必须保持不变，须用“绝对地址”表示。第三个参数是可选参数，可以取0或1，取0时，表示第一个参数（变量）的值越大，排位越靠前，省略该参数时相当于取值为0。若第三个参数取1，则第一个参数（变量）值越小，排位越靠前。

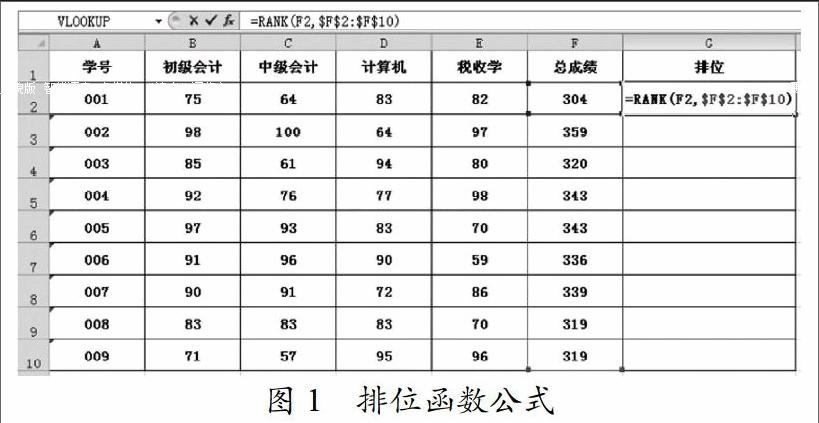
该例是按“总成绩”进行排位的，G2中的公式为RANK（F2，$F$2：$F$10）。F列上的数据就是函数中的“变量”，其中F2必须用相对地址表示，在对G2中的公式向下“拷贝”的过程中，F2自动变更为F3、F4、F5一直到F10。第2个参数$F$2：$F$10是“总成绩”字段区域，既所有自变量所在的区域，须用绝对地址表示，以保证在对排位函数“拷贝”的过程中这个区域始终保持不变。此公式仅用了两个参数，省略第三个参数表明：总成绩高的排位号在前。拖G2单元格的“填充柄”向下“拷贝”时，单个学生的总成绩不断在变化，而所有学生的总成绩区域被“锁住”，拷贝到最后一个学生，即可快速得到整个“排名”字段。

另外，在实际工作时，某些公式中的常数有可能发生变化。如请假扣款金额、计件工资金额等，当把这些常数直接写在公式中时，一旦发生金额变化，就需要重新进行计算。最好的方法是在将该常数先放在表格中的某单元格处，而在公式中用该单元格的绝对地址表示，就可以实现在金额变化后，所有应用该金额的地方会自动更新。

EXCEL单元格地址的第三种表示方法是：混合地址表示法。他是介于相对地址和绝对地址表示之间的一种地址表示方法，这种表示方法中的自变量在跟随因变量变化的过程中受到一定的限制，仅能沿行方向变化或沿列方向变化。这种变量地址表示方法主要用于制作类似于九九乘法表的“交叉数据表”。当一个公式或函数中有多个变量时，提取两个相互独立的变量分别放在行和列上，并设定一个变化序列，相当于建立了一个二维的X-Y坐标系。再利用EXCEL的运算特点：相同运算仅计算一次，其他数据通过拷贝得到，就可以快速地制作一个函数F（X，Y）的平面数据表，我们中学用的《常用数学用表》可以利用这种方法快速地制作。

“混合地址”表示方法是仅在列标或行号前加$号。如$D6、A$8。其中，$D6表示Y方向变化的变量，即数据仅限于在D列上变化。A$8表示X方向变化的变量，该数据仅于在第8行上变化。也就是说，前面有$号的行或列，就是被限定变化的区域。

下面以制作两数和的立方表为例，介绍变量的“相对地址”表示方法在制作“交叉运算表”时的应用。图2为一最简单的X-Y 坐标系，自变量分别沿第一行和第一列放置。

在表中任意一个单元格中输入公式均可，但考虑到“拷贝”公式的方便，最好在坐标系左上角的B2单元格中输入计算公式：=（B$1+$A2）^3，如图2所示。

公式输入完毕后，在水平和垂直方向上分别拖动一次“填充柄”进行“拷贝”，即可完成整表制作。

EXCEL单元格地址的三种表示方法是EXCEL的精髓，是深入学习EXCEL的基础。许多使用EXCEL制表的人仅仅接触到“相对地址”表示方法，也只能制作最简单的数据库类型的表格。只有熟练地掌握三种地址表示方法才能解决更多的应用问题，才能拓展EXCEL的应用领域。