基于MATLAB程序实现测量不确定度评定的可行性分析

基于MATLAB程序实现测量不确定度评定的可行性分析

李慧奇1，王凯红1，张秦2，王永辉2

(1.华北电力大学，河北保定071003；2.国网河北省电力公司电力科学研究院，石家庄050021)

摘要：针对传统GUM法评定过程繁琐、计算复杂的问题，提出基于MATLAB程序实现测量不确定度评定的方法，介绍MATLAB程序，分析MATLAB程序在测量不确定度评定过程中的应用步骤及效果，结果表明基于MATLAB程序得到的测量不确定度评定结果与传统GUM法非常接近，验证了基于MATLAB程序进行测量不确定度评定的可行性。

关键词：GUM；MATLAB；测量不确定度

收稿日期：2014-10-17

作者简介：李慧奇(1970—)，男，副教授，主要研究方向为电工理论与新技术。

中图分类号：TM933

文献标志码：B

文章编号：1001-9898(2015)01-0012-03

Abstract：Because the evaluation process of traditional GUM method is complicated and complex, this paper presents the evaluation of Measurement Uncertainty based on MATLAB, introduces the MATLAB program, analyzes MATLAB program procedure and the effect in the process of evaluation of Measurement Uncertainty, the result shows that the result of MATLAB method and GUM method is very close, finally, verifies the feasibility of evaluation of measurement uncertainty based on MATLAB.

Feasibility Analysis on Measurement Uncertainty Evaluation Based on MATLAB

Li Huiqi1,Wang Kaihong1,Zhang Qin2,Wang Yonghui2

(1.North China Electric Power University, Baoding, 071003，China; 2.State Grid Hebei Electric Power Research Institute，Shijiazhuang 050021，China)

Key words：GUM；MATLAB；Measurement Uncertainty

在测量过程中，由于方法、设备、人员、环境等因素的影响，不可避免存在误差，测量结果具有不确定性。随着生产的发展和科技的进步，对测量数据的准确性和可靠性提出了更高的要求。不确定度作为评定测量结果质量高低的一个重要指标，显得极其重要。

测量不确定度是表征合理地赋予被测量之值的分散性，与测量结果相联系的参数。测量不确定度只说明被测量之值的分散性，而不说明测量结果是否接近真值[1]。测量不确定度的评定前提是：不考虑失误值，已知的系统影响已修正。GUM法是测量不确定度评定最常用和最基本的方法，应按照国家计量技术规范中的原则、方法和步骤进行评定。文献[1-3]按照GUM法进行测量不确定度评定，均未进行数据的预处理，而且评定过程比较复杂，数据计算量大。基于MATLAB编程可以实现测量不确定度的评定过程，避免了繁琐的手工计算，准确性更高，耗费时间更短。

1MATLAB程序介绍

MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言。MATLAB统计工具箱中有各种随机数发生器程序，如正态分布、t分布、均匀分布、对数分布等，只需要调用就可以产生大量的随机数[4]。文献[5]给出的蒙特卡洛法是一种基于随机数的计算方法，通过建立一个概率模型或随机过程，对模型或过程的随机采样来计算所求参数的统计特性[6-7]。

2MATLAB程序的应用

2.1　测量数据预处理

由于某种不正常原因造成的粗大误差是偶尔的，常通过判别而剔除异常数据，格罗布斯准则可靠性高，判别效果较好[1，8-9]。

将测量数据xi按大小顺序排列成顺序统计量x(i)，即取定显著度α=0.05，查表可得临界值g0(n,α)。

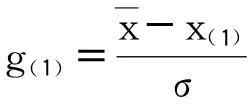
(1)

(2)

当g(i)≥g0(n,α)时，即判别该测得值含有粗大误差，应予剔除。

系统误差是由于测量设备、方法、原理的不完善、不正确或环境发生变化而引起的，是有规律性的。对于系统误差的处理应发现它、消除它，并对测量数据予以修正。可用不同公式计算标准差比较法发现系统误差[1,8]。

(3)

(4)

(5)

(6)

则怀疑测量列中存在系统误差。

2.2　GUM法评定测量不确定度

2.2.1测量条件

a. 测量依据：JJG 1052-2009《回路电阻测试仪、直阻仪》[10]。

b. 测量环境条件：温度为(23±5)℃；相对湿度为40%~75%RH；电压变化不超过电源额定电压的±10%。

c. 测量标准器：MJZ-600型模拟大功率交直流标准电阻器，电流测量范围为1～600 A；交直流电阻测量范围为0.001 ～60×103mΩ[10]。

d. 被测对象：BZC3395型变压器直流电阻测试仪，示值误差为0.2%。

e. 测量过程：采用模拟大功率交直流标准电阻器作为标准设备，用标准电阻法测量变压器直流电阻测试仪的直流电阻示值误差。将标准设备和被检测试仪的电流端、电位端、屏蔽端和接地端分别相连接，根据被检测试仪电流大小设置好标准设备的量程档位后开始测试，当被检测试仪工作电流稳定后，分别记录标准设备和被检测试仪的直流电阻值。

2.2.2测量模型

ΔR=Rx-Rn

式中：Rx为变压器直流电阻测试仪的直流电阻示值；Rn为标准电阻器的直流电阻实际值；ΔR为直流电阻示值的绝对误差。

2.2.3A类标准不确定度的评定

A类标准不确定度主要是由变压器直流电阻测试仪测量不重复引起的。根据测量模型，测量结果不确定度来源于Rx变压器直流电阻测试仪和Rn标准电阻器。

对1台BZC3395型变压器直流电阻测试仪100 mΩ点，连续进行10次独立测量，每次测量均在直流电流为10 A的条件下，得到一组测量数据：99.99，99.99，99.97，99.98，100.0, 99.97，99.97，99.99，100.0，100.0 mΩ。

测量数据的均值为：

(7)

单次实验标准差：

2.2.3.1判别粗大误差

从上述测量数据中可知：最大值x(10)=100.0 mΩ；最小值x(1)=99.97 mΩ。查表可得临界值g0(10, 0.05)=2.18。

若认为x(1)=99.97 mΩ可疑，则有

若认为x(10)=100.0 mΩ可疑，则有

由以上可知：g(1)≤g0(10, 0.05)，g(10)≤g0(10, 0.05)。则可认为该组测量数据不含有粗大误差。

2.2.3.2判别系统误差

上述测量数据，按贝塞尔公式可得σ1=σ=0.012 65 mΩ；按别捷尔斯公式可得：

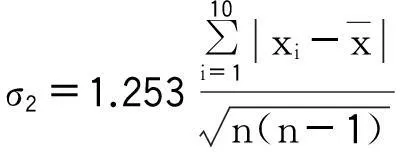
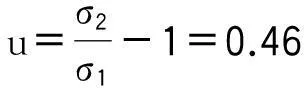
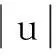
则测量数据中不含有系统误差。

2.2.3.3计算标准不确定度

测量结果的标准不确定度为:

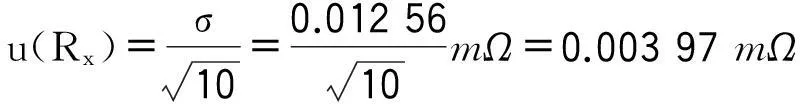
自由度为：v1=n-1=10-1=9

2.2.4B类标准不确定度的评定

标准电阻器Rn的标准不确定度u(Rn)主要由标准电阻器误差引起的，采用B类评定方法。

由于说明书中给出标准电阻器的分辨率为0.002μΩ，由分辨率引起的不确定度与标准电阻器误差引起的不确定度相比可忽略；另外受温度、湿度变化等其他因素影响的不确定度是极其微小的，也在此忽略[11]。

2.2.5合成标准不确定度的评定

在标准不确定度合成前，将所有通过A类评定和B类评定得到的标准不确定度汇总于表1，以便查看各输入量标准不确定度的情况[12-14]。

表1标准不确定度汇总表

标准不确定度分量u(Rx)u(Rn)不确定度来源测量不重复标准电阻器误差标准不确定度0.00397mΩ0.0289mΩ灵敏系数Cj1-1自由度vj950

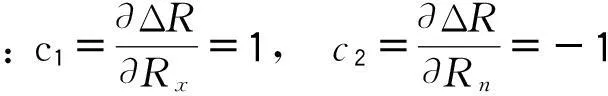
由于变压器直流电阻测试仪Rx和标准电阻器Rn彼此独立，合成标准不确定度可按下式得到：

合成标准不确定度的有效自由度为：

2.2.6扩展不确定度的评定

取包含概率p=95%，veff=52，查t分布表并将有效自由度近似取整为50得：

k95=t95(veff)=t95(50)=2.01

扩展不确定度U95为：

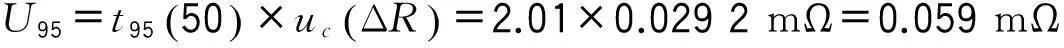
2.3　 MATLAB程序应用效果

MATLAB程序流程示意见图1。

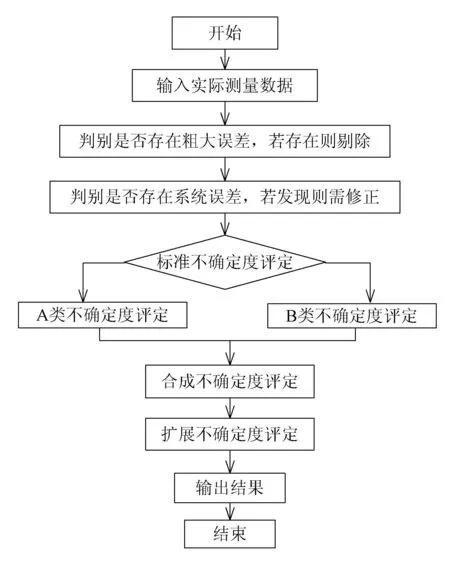
图1　程序流程示意

将变压器直流电阻测试仪的测量数据输入MATLAB程序，运行后结果为：合成不确定度Uc=0.029 1 mΩ，扩展不确定度Up=0.058 6 mΩ。与传统GUM法计算结果基本一致，验证了基于MATLAB程序进行测量不确定度评定的可行性。

3结论

a. 基于MATLAB程序实现测量不确定度评定过程，避免了繁琐的手工计算，准确性更高，耗费时间更短;

b. 运用传统GUM法进行测量不确定度评定时，往往不注重异常数据的处理问题，建议应首先对数据进行预处理，判别是否存在粗大误差和系统误差，然后再进行测量不确定度评定。

参考文献：

[1]刘玮蔚.数字式绝缘电阻表测量不确定度的分析与评定[J].河南电力, 2012, 3: 5-6,9.

[2]吴瀛,祁舒喆.电测量变送器检定装置测量结果不确定度评定[J].南方电网技术, 2012(6),4:84-86.

[3]孔伟民.用5 520 A建立数字多用表校准装置测量不确定度评定[J].电子质量, 2013,11:66-70.

[4]林成.工程测量数据误差及其Matlab处理[J].吉林水利, 2013(10):32-34.

[5]中华人民共和国国家质量检验检疫总局，中国国家标准管理委员会，JJF 1059.2-2012用蒙特卡洛法评定测量不确定度[M].北京：中国计量出版社，2012.

[6]上海市计量测试技术研究院.常用测量不确定度评定方法及应用实例[M].北京:中国计量出版社, 2000.

[7]杨建.蒙特卡罗法评定测量不确定度中相关随机变量的MATLAB实现[J].计测技术,2012,32(4): 51-54.

[8]赵志刚,赵伟,测量不确定度理论研究和应用中的若干热点问题[J].电测与仪表,2007,44(3): 1-4.

[9]葛欣宏,贺庚贤,宁飞.防静电工作区接地电阻的测量不确定度评定[J].电测与仪表, 2013,50(9):46-50.

[10]JJG 1052-2009,回路电阻测试仪、直阻仪[S].

[11]臧景茹.直流数字电压表法校准电阻箱测量不确定度的评定[J].电测与仪表, 2004(6),41(462):31-33.

[12]JJF 1059—2012,测量不确定度评定与表示[S].

[13]李慎安.关注JJF 1059.1—2012《测量不确定度评定与表示》新规范[J].工业计量,2013,23(3):49-50.

[14]费业泰.误差理论与数据处理第四版[M].北京:机械工业出版社,2000.

本文责任编辑：杨秀敏