高分辨固体核磁共振技术在材料化学研究中的应用

高分辨固体核磁共振技术在材料化学研究中的应用

徐大江1舒婕2*

(1.哈尔滨市产品质量监督检验院，哈尔滨 150036；2.苏州大学分析测试中心，苏州 215123)

摘要：近年来，高分辨固体核磁共振技术(SSNMR)发展迅速，其在化学材料研究领域的应用价值日益显现。本文第一部分简述了化学研究中常用的SSNMR脉冲高分辨技术，包括同核和异核去偶技术以及偶极重聚技术等。第二部分结合具体的实验方法和实例，重点介绍SSNMR技术在材料研究中的应用。首先，使用一维谱实验、二维化学位移相关谱实验来实现分子化学结构和聚集态结构的研究；然后，通过同核偶极偶合常数的测量来计算原子核间的距离信息；此外，交叉极化定量实验可以实现样品体系结构和组分的定量表征；最后，通过对异核偶极偶合常数的测量、线型分析以及弛豫时间的测量等方法来实现固体材料分子动力学行为的研究。

关键词：固体核磁共振；材料化学；高分辨技术；交叉极化

作者简介：徐大江， 1982年出生，2013年哈尔滨理工大学材料工程领域工程硕士毕业,现就职于国家农林副产品检验中心。

通讯作者：*舒婕，女，1982年出生，博士研究生，副研究员，主要从事固体核磁共振方法与应用的研究，E-mail：shujie@suda.edu.cn。

DOI:10.3936/j.issn.1001-232x.2015.01.005

收稿日期：2014-07-07

基金项目:重庆市大学生创新创业训练项目(201310637011)，国家自然

Application of high-resolution solid-state nuclear magnetic resonance techniques in chemical materials.XuDajiang1,ShuJie2*(1.AnalysisandTestingCenter,SuzhouUniversity,Suzhou215123,China; 2.CompositiveAnalysisDepartmentofHarbinProductQualitySupervisionandInspectionCenter,Haerbin150036,China)

Abstract:In the first section of this article, we briefly overview the high-resolution (SSNMR) techniques.In the second section, combinded with experimental method and concrete examples, the application of SSMMR tecnology in material research is introdnced.

Key words：solid-state nuclear magnetic resonance; chemical materials; high-resolution technique; cross polarization

1引言

近年来，固体核磁共振(Solid State Nuclear Magnetic Resonance，SSNMR)理论和实验技术发展迅速[1-6]，在化学领域的结构研究中所发挥的作用日益显现。与液体高分辨核磁共振技术相比，人们对SSNMR检测手段的需求主要有以下两个方面：首先，许多化学物质的分子结构无法在溶液状态下进行检测，如交联高分子，催化材料，石墨烯等；其次，物质在固体状态下所特有结构信息，对物质的性质有重要的影响，而在溶液状态下，这些结构信息将消失，如纳米材料，有机导电材料和太阳能电池材料等。SSNMR技术可以定量或定性的研究物质在固体状态下聚集形态、相尺寸与结构、分子间的距离，以及固体状态下分子间的相互作用和动力学行为等[4-6]，从而为研究体系性能与微观结构的关系提供了宝贵的信息。

然而，与溶液NMR相比，SSNMR谱图灵敏度与分辨率较低。这是因为在固体状态下，分子运动受到了限制，因而无法平均掉原子核之间以及原子核与外场之间的相互作用。这些相互作用主要包括：化学位移各向异性、偶极偶合、四极矩偶合等[1,3]。为了提高SSNMR谱图的分辨率及灵敏度，许多NMR学者致力于高分辨技术的研究，他们通过对谱仪硬件的提升以及脉冲序列的巧妙设计，试图消除或削弱这些使谱峰增宽的相互作用，期望使SSNMR谱图在提供丰富的固态结构信息的同时，其分辨率可以向溶液NMR谱图靠近。从而实现SSNMR在化学结构研究领域中的普适性。本文将简要介绍目前常用的高分辨SSNMR脉冲技术和实验，并通过多个实例来展示SSNMR技术在材料化学研究中的应用价值。

2多样化的高分辨脉冲实验技术

上世纪50年代末，E. R. Andrew[7]和I. J. Lowe[8]等分别提出的魔角旋转技术(MAS)，巧妙且高效的提升了SSNMR谱的分辨率，但是魔角旋转速率受限于实验室硬件和技术条件，不可随意增减。多样化的高分辨脉冲实验技术可弥补上述硬件的不足，从而快捷、巧妙地提高SSNMR谱图的分辨率，使SSNMR实验在化学结构研究中具有更高的应用价值。

图1 　 13C交叉极化(CP)和单脉冲实验(SPE)谱图对比及脉冲序列示意图 (a) 13C CP谱(上)和L-丙氨酸的 13C SPE谱(下)；(b) 13C CP实验的脉冲序列；(c) 13C SPE 实验的脉冲序列。

2.1　交叉极化技术(Cross Polarization-CP)

交叉极化(CP)是SSNMR中最基本最重要的实验技术之一。在固体状态下，13C、29Si等天然丰度低的核自旋体系具有较低灵敏度和较长的自旋-晶格弛豫时间(T1)，在使用单脉冲(SPE)实验技术进行测量时，往往耗费很长的实验时间也无法得到理想的高分辨谱图。交叉极化技术不仅可以实现Hartman-Hahn[9]条件下由富核(I)到稀核(S)的极化传递，增强稀核的信噪比，而且只要等待3～5倍于富核T1的弛豫延迟时间。因此与SPE实验相比，CP技术即节省了实验时间又提高了信噪比。如图1(a)为L-丙氨酸粉末样品在相同实验时间下的CP谱和SPE谱，图1(b)和(c)分别为两种实验的脉冲序列示意图。由图可知，相同的实验时间下，CP谱的信噪比较SPE谱有显著的提升。

2.2　异核去偶技术 [10]

以1H-13C体系为例，在观测13C核时，1H-13C之间的异核偶合会导致13C谱的谱峰增宽，为去除此异核偶合作用，可以在13C采样期间在1H通道发射一个连续波脉冲，使1H核共振并处于饱和状态，从而抑制1H-13C之间的偶合作用。由于1H-13C偶极偶合较大，因而连续波所需的功率非常高，一般大于60kHz，这就是连续波高功率去偶技术。随着NMR谱仪硬件技术的提高，高功率连续波去偶技术在高的MAS转速和高静磁场的实验条件下，效果并不理想。因而人们发展了一系列多脉冲异核去偶技术，包括TPPM、SPINAL-64、PISSARO和XIX等[11，12]，解决了上述问题。如图2，下方谱图为L-丙氨酸晶体粉末样品的13C SPE谱，与未对氢去偶的13C SPE谱相比(上方)，TPPM异核去偶技术使13C谱的谱峰明显窄化。

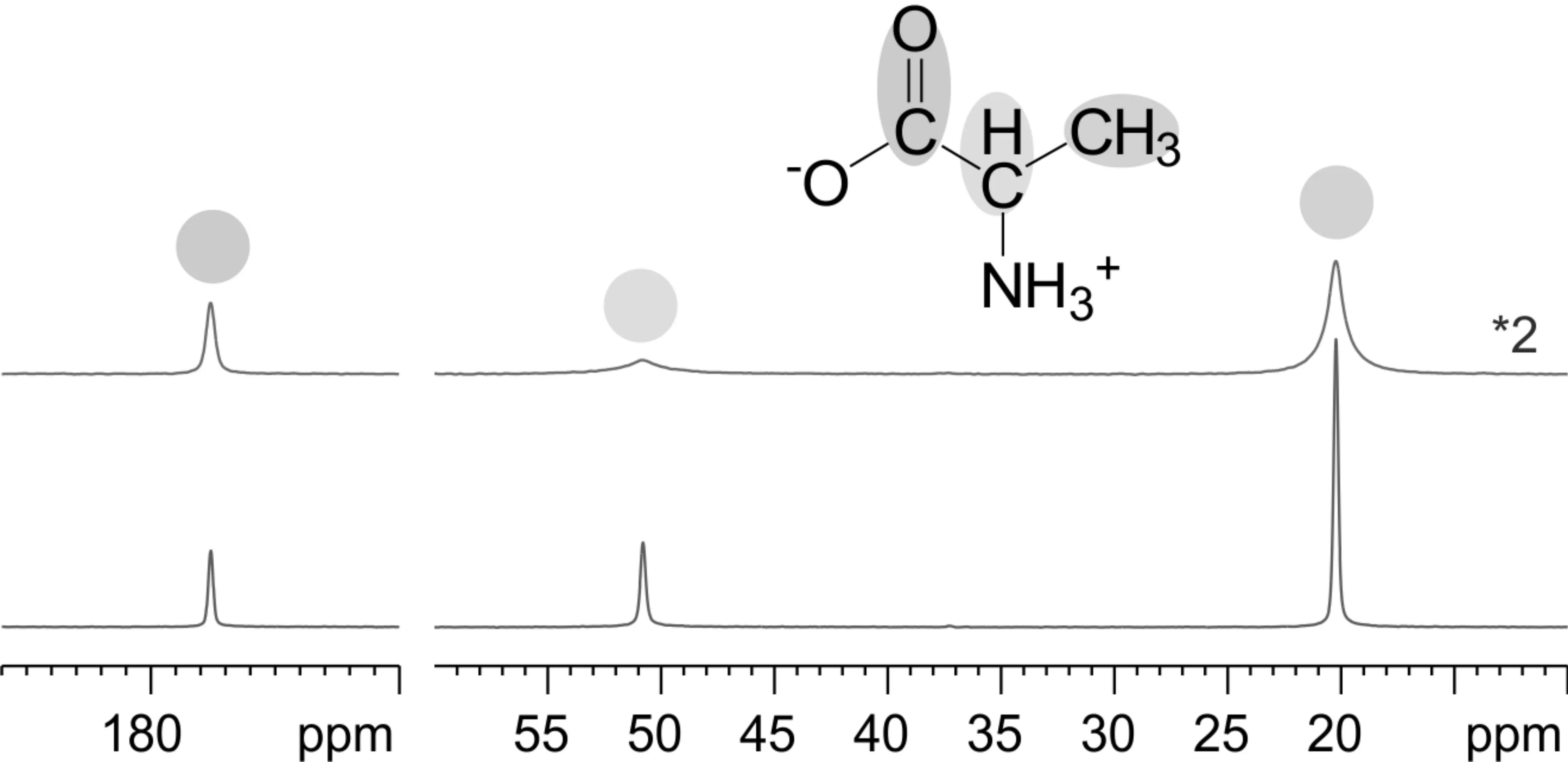
图2　L-丙氨酸样品异核去偶技术 13C SPE对比图谱 使用TPPM异核去偶技术(下)；未使用异核去偶技术(上)

2.3　同核去偶技术

对于自然丰度较高的同核(I)体系来说，如1H体系，魔角旋转技术可以在一定程度上提高NMR谱图的分辨率。然而，由于硬件的限制，魔角旋转速率并不能无限提高。为了解决这一局限性，NMR学者发展了一系列组合脉冲技术，如FSLG[13,14]，PMLG[13,15]，DUMBO[16]和eDUMBO[17]等，通过对核自旋空间的操作来有效减弱同核之间的偶极偶合。同时结合魔角旋转技术，可以进一步提高富核SSNMR谱的分辨率。这种将MAS与多脉冲技术相结合的同核去偶方法已广泛的应用于I核(如1H)高分辨SSNMR的一维及多维谱中，对于偶极偶合致宽的谱峰有显著的去偶效果。该方法在SSNMR领域中称为CRAMPS技术。图3为甘氨酸粉末样品在18kHzMAS 转速及CRAMPS技术下的1H NMR谱。在使用CRAMPS技术后，谱图的分辨率有明显的改善，CH2基团的两个氢可完全分辨。

图3　18kHzMAS条件下甘氨酸粉末样品的 1H SSNMR谱对比示意图。 未使用CRAMPS技术(上)；使用CRAMPS技术(下)

2.4　偶合重聚技术

高分辨固体核磁共振技术的发展，使SSNMR在固体样品的化学与物理结构、分子运动、相转变等问题的表征方面发挥着不可替代的作用。但与此同时，人们认识到为了实现高分辨而消除的各种相互作用中包含了很多可以反映固态样品物理、化学性质的重要信息，这本是SSNMR优越于溶液NMR的方面。因此NMR学者发展了一系列新技术，将高分辨技术平均掉的各种相互作用选择性地重新获取，这类技术被统称为偶合重聚技术(Recoupling)。偶合重聚技术主要包括同核偶极偶合重聚技术，如BaBa[18]，CN[19]，RN symmetry[20]等,异核偶极偶合重聚技术，如REDOR技术[21]；以及化学位移各向异性重聚技术，如SUPER[22]，CN，RN symmetry 等[23]。使用这些技术一方面可以提取出原子核间的偶合强度，从而得到有关核间距离或局部运动性能的信息。另一方面，将该技术与SSNMR的其他SSNMR技术相组合，可以发展出一系列固体高分辨同核、异核的相关实验[24-27]，为固体体系的化学结构研究提供了丰富的定性与定量的信息。

2.5　四极矩核的SSNMR高分辨实验

SSNMR可观测的核中，74%都是四极矩核。根据自旋量子数的不同可以将其分为整数四极自旋核 (如2H、6Li等) 和半整数四极自旋核(如11B、17O、23Na、27Al等)。在整数四极自旋核中，NMR学者对氘核2H (I=1)的研究比较普遍，特别是分子动力学的研究。这是因为氘核的四极矩偶合相对较小，一般在160～190kHz之间。然而其他的整数四极自旋核都有很高的四极偶合强度，一般可达MHz的数量级。根据笔者的了解，目前尚无有效的去偶方法来研究这一类原子核。

与整数四极自旋核不同，对于半整数自旋核来说，目前已有四种技术可以有效获取高分辨的NMR谱图，包括MAS、DOR[28]、DAS[29]和MQMAS[30]。其中，MQMAS的应用范围较广。与其他方法相比，MQMAS方法对实验硬件的要求较低，并且通过二维谱的方式提供了分辨率较为理想的四极核SSNMR谱图。J.P.Amoureux小组基于该方法结合各种常规去偶及偶合重聚技术，提出了一系列半整数四级核的同核及异核相关谱[31]。为金属-有机、无机材料等体系的结构研究开辟了多种方法。

3高分辨固体核磁共振技术在材料化学研究中的应用

3.1　化学分子聚集形态的研究

SSNMR作为化学领域的分析工具，最被化学者所了解的是对合成产物的结构鉴定[32]。然而，除此之外，SSNMR在研究固体分子结构及聚集形态方面发挥了重要作用。主要包括了固态体系分子相互作用、结晶体系中分子堆叠结构及相变过程[33]、高分子材料相结构及相尺寸的表征[34]、共混材料相容性的研究[35]、多孔材料(如催化剂)微观结构[36]，以及分子尺度上原子核间距离的测量等等。此外，结合X射线衍射(XRD)等表征方法，可系统精确地表征研究体系的微观结构，关联其宏观性能，可以帮助揭示功能材料的工作机理，促进对相关领域的认知与发展[33,37,38]。

3.1.1同核化学位移相关谱 (HOMCOR )

以1H-1H 同核化学位移相关谱为例，按照量子演化的方式，一般分为单量子-单量子(SQ-SQ)同核相关谱和双量子-单量子(DQ-SQ)同核相关谱。图4(a)、(b)为这两种二维谱的示意图。SQ-SQ谱的脉冲序列如图4(c)。 该实验操作简单，但谱图中的对角峰无意义。而DQ-SQ实验则需要使用同核偶极偶合重聚技术，如BaBa, CN, RN symmetry等，应用于图4(d) 中的深阴影区域。并且结合转子同步技术和相位循环来实现t1时域上DQ的演化。DQ-SQ谱优于SQ-SQ谱最重要的一点就是其对角峰同交叉峰一样提供分子结构的信息。当实验的偶极偶合重聚时间小于30μs时，DQ-SQ图中的相关峰说明了化学位移对应的两个原子核的空间距离小于4Å[40]。如图4(b)中，原子核a与b，a与a，b与b之间都显示出了相关峰，说明他们的空间距离都在4Å以内。而 图4(a)，只能说明a与b接近，但无法说明a与a之间以及b与b之间的距离信息。

图4　同核化学位移二维相关谱示意图 (a)单量子-单量子(SQ-SQ) ； (b)双量子-单量子(DQ-SQ) ；(c)和(d)分别为所使用的脉冲序列示意图。

3.1.2异核化学位移相关谱 ( HETCOR)

异核化学位移相关谱(HETCOR)是反应不同种核之间距离或相互作等相关信息的二维或多维谱图，如13C-1H,15N-13C以及31P-1H之间等等。其中，不同于HOMCOR实验，HETOCR的实验方法更加多样化。在设计实验脉冲序列时，既可以改变相关信息传递的路径(13C→1H，1H→13C，13C→13C，1H→1H)，也可以任意变换极化传递的方法。常用的极化传递的方法有CP[25]和REPT[26]，其中为了抑制氢核之间的自旋扩散作用，实验中往往结合同核去偶技术。

应用同核、异核二维相关谱，不仅可以进行类似于溶液NMR中对分子结构的分析，并且可以研究固体材料分子间的相互作用。此外，通过对同核、异核二维相关谱中化学位移与相关信息的分析，可帮助研究分子的局部堆叠结构，为揭示功能材料的微观结构机理提供帮助。图5(a)为有机腙的衍生物，命名为D5，常温下具有导电性能。为揭示其导电机理，实验对该体系分子聚集结构进行了研究。如图5(c)为D5的2D1H-1H DQ-SQ化学位移相关谱，谱图中各组相关峰清晰可辨，表现出理想的分辨率，说明了研究体系为有序结构。此外，图5(b)中，与溶液1H谱相比较，常温固态下D5的两种-NH基团的化学位移向高场移动，并裂分出三个峰。对于参与π-π堆叠的有机分子体系，当氢原子受到了相邻分子中π电子云的屏蔽作用，其化学位移将会向高场移动。化学位移值改变的多少取决于分子间的距离和堆叠的结构。这是SSNMR1H谱检测有机体系π-π堆叠结构是否形成的特征方法。因此，通过比较溶液和固态D5的NMR1H谱化学位移，可知常温固态的D5存在两种π-π堆叠的有序结构，分别对应于两种-NH-基团的13.6ppm、14.2ppm和11.0 ppm、11.7ppm。这一结论也可通过13C {1H} FSLG-HETCOR(图5(d))中a、h位芳香氢的裂分进一步证实。同时，两种NH在14.2ppm和11.7ppm的谱峰与溶液NMR1H谱的化学位移(14.7ppm和11.6ppm)相近，说明固态D5体系中仍有少量分子游离于有序的堆叠结构之外。结合2D WAXS和化学位移计算，D5两种有序结构可精确测量[33]，结构模型如图5(e)和(f)所示。

图5的衍生物D5的固体核磁数据示意图 (a)有机化合物D5的分子结构示意图；(b)D5 1D 1H 谱，谱峰归属的颜色标记参考结构图。与溶液NMR谱对比，两种NH基团的化学位移值如表中所示；(c) 2D 1H- 1H DQ-SQ化学位移相关谱; (d) 13C { 1H} FSLG-HETCOR 芳香区域截图;(e)D5堆叠模型I; (f)D5堆叠模型ii。

3.2　原子核间距离的测量

在二维谱中，被重聚的偶极偶合作用是相关自旋对沟通的桥梁。不仅如此，相关自旋对之间的偶极偶合强度还可以准确提供核间距离的信息。对于刚性基团中的自旋对，其间的偶合常数Dij与自旋对间的距离的负三次方r-3成正比。因而准确的测量偶极偶合常数便可计算出自旋原子核对间的距离。

NMR学者提出了多种用于测量核间距离的实验方法，但这些方法的核心都是通过对偶合常数的测量来间接得到距离的信息[39]。图6是其中的两种测量同核间距离信息的实验脉冲序列。图6(a)为BaBa同核双量子边带谱[40]，图6(b)是 BaBa双量子演化实验[41]。两种方法分别适用于两核体系和多核体系的偶极偶合常数的测量，从而计算出相应的距离信息。

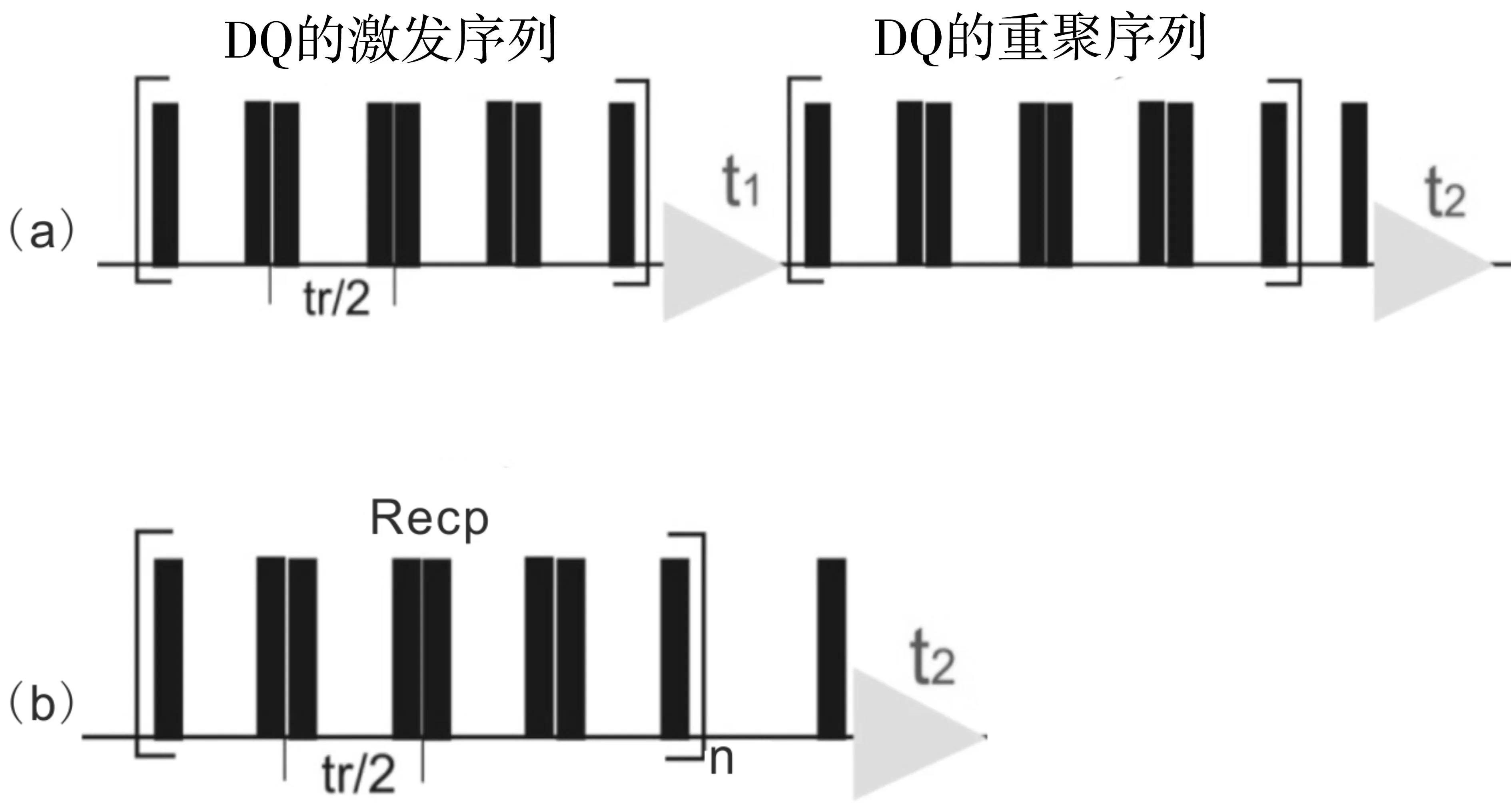
图6　用于测量同核间距离信息的实验脉冲序列 (a) DQ边带谱实验脉冲序列示意图；(b)DQ演化实验脉冲序列示意图。

图7　PDI1固体核磁共振实验数据。 (a) PDI1结构示意图; (b) PDI1晶体的2D BaBa DQ-SQ谱图，谱峰归属如图所示；(c) PDI1中2位氢的DQ边带实验谱图(灰色)和计算机拟合谱图(黑色)。

3.3　结构和组分的定量表征

SSNMR的表征方法不仅仅局限于结构的表征，同时还可以提供定量的信息,包括分子基团比例、共混物组分的含量等。此外固NMR还可以半定量或定量的分析多相高分子的相尺寸、结晶度等等[42-45]。

SSNMR实验中，一般选用化学位移范围宽且自然丰度低的原子核S，如13C、29Si等进行检测，并通过SPE实验对样品进行结构或组分的定量分析。然而，一般固体样品的S自旋晶格弛豫时间(T1)很长，因而采集一张定量的SSPE谱需要很长的实验时间。基于此因，许多NMR学者陆续提出了一些省时高效的SSNMR定量方法，其中以实现CP定量性的方法居多。包括通过S核间自旋扩散实现定量的QUCP方法[46,47]、用于测量高分子体系结晶度的CP/spin diffusion定量方法[48,49]以及基于交叉极化互易定理并具有普遍适用性的QCP/QCPRC[50]和SPCP方法[51]等等。为快速准确地实现固体材料中结构、组分或化学基团的定量表征提供了多种选择方法。

表1　CP、QCP和SPE方法对NP1和NP2样品的定量研究结果

图8　P1和NP2样品化学结构及交叉极化硅谱示意图。 (a) NP1和NP2样品的化学结构示意图；(b) NP1样品 29Si CP 谱.

3.4　分子动力学的研究

SSNMR方法的另一应用方向是对分子动力学行为的研究(Local Dynamics)。包括定性描述分子或分子基团及高分子局部链段的运动性，定量分析高分子分子链和液晶分子的运动方式及有序度，此外，还可以追踪高分子链段或小分子在样品体系中的空间及化学交换行为等。SSNMR对于时域范围不同的动力学行为的研究，所使用的实验方法也各不相同。

3.4.1弛豫时间

自旋晶格弛豫时间(T1)是表征原子核在静磁场下磁化矢量从激发态到平衡态弛豫快慢的NMR参数。它的大小受到静磁场强度和原子核运动频率的影响。以结晶聚合物体系为例，不同相结构的分子链所处的环境不同。一般来说，结晶区的分子链排列规整，分子链的运动自由度低，其S核的T1较长；而非晶区的分子链受限相对较小，运动性较强，其S核的T1较短。SSNMR实验中，T1可以反应出10-9-10-6s尺度上分子的运动信息[42-44]，结合温度的变化，可以进一步研究聚合物材料的性能及分子链的动态信息[53]。此外，自旋-自旋弛豫时间(T2)和旋转坐标系下的自旋-晶格弛豫时间(T1ρ)等参数同样是表征原子核的弛豫行为的参数。不同的是，在研究分子动力学时，这些参数所表征的时间尺度不同。T2表征10-4～10-3s的运动行为，而T1ρ则适用于10-6～10-5s 范围内的运动行为的研究。

3.4.2边带谱图(sideband pattern)[26,27]

以13C-1H体系为例，如图9(a)和(b)为常用的边带谱的实验脉冲序列。其中，图9(a)为REPT-HDOR 边带实验，图9(b)为REREDOR边带实验。REPT-HDOR实验方法可以定量表征分子中CH基团的动力学行为，而REREDOR实验不仅可以研究CH基团，还可以定量的分析分子中的CH2和CH3基团的动力学行为。图9(c)和(d),分别为CH 和CH2基团的13C{1H} REREDOR模拟图。由图可知，边带谱的线型对研究体系的运动性十分敏感，因而通过实验拟合边带谱图而得到的分子局部运动信息，准确并可靠。

图9　带谱图法测量异核偶极偶合常数 (a)REPT-HDOR实验脉冲序列；(b)REREDOR实验脉冲序列；(c)计算机模拟的不同有序度的CH基团；(d)CH 2基团的REREDOR边带谱图。

SSNMR表征分子局部运动性能，不仅可以研究材料体系的动力学行为，也可通过运动行为的变化推断分子的空间结构。图10为0Fs(metal-organic frameworks)体系Al-4的合成示意图。为了证明空间有序结构的形成，实验通过13C{1H} REPT-HDOR边带谱图定量表征有机单元局部基团的动力学行为。

图10　 Al-4合成示意图

图11(c)为TPB在形成MOF后的REPT-HDOR边带谱图。通过对三种CH基团边带谱峰的拟合及计算，可以得到偶极偶合分别为21kHz、5～7kHz和5～7kH，相应的有序度为1.0、0.25～0.33和0.24～0.33(图11(d)～(f))。当有序度为1时，基团在自相关时间为10-1μs量级的运动时域上表现为静止状态；当有序度为零时，基团做完全无规运动。因而，位点1的CH基团为静止状态，而位点4、5的CH基团的运动性能介于两者之间(图11(a))。通过对分子结构的分析，当形成空间络合结构后，位点4和5应该具有相同的运动性能，这与测试结果相同。此外，该运动方式只能是轴向运动。 通过对苯环轴向分子运动的模拟[56]，可以得出，快速轴向翻转运动的有序度为0.12，而180°两点翻转运动的有序度为0.62。由上述数据可得，位于三角处的三个苯环的运动方式介于快速轴向旋转和180°两点翻转之间，且翻转角度呈±69°～±87°高斯分布，而中心苯环则处于静止状态。 对于自由的TPB小分子来说，位点4，5的运动性不一定相同，且中心苯环的静止状态也是不可能存在的。 因而，上述的动力学行为说明了新的MOF结晶结构的形成。

图11　Al-4的局部分子动力学研究 (a)Al-4中有机单元局部运动；(b),(c)AL-4 2D REPT-HDOR谱；(d)～(f)Al-4三种CH基团的一维REPT-HDOR实验边带谱图(灰色)及其拟合谱(黑色)。

3.4.3线型分析

当原子核的运动频率与核自旋的各向异性作用频率相当时，可通过对粉末谱的线型分析来研究运动行为。化学位移各向异性谱对10-4～10-3s频率范围的运动行为十分敏感，可以提供分子局部运动行为的信息。为了在提高分辨率的同时，实现各向异性谱的采集，实验往往会使用二维各向异性谱，如，2D SUPER[22]等。

对于2H富集的样品，10-6～10-4s的运动行为可以通过2H谱的峰形来研究[57,58]。与化学位移各向异性谱相似，由于2H谱的峰形对运动行为十分敏感，因而结合计算机拟合可以定量的分析该频率范围的运动行为。 如图12是不同基团的运动方式下，计算机模拟的2H谱图。

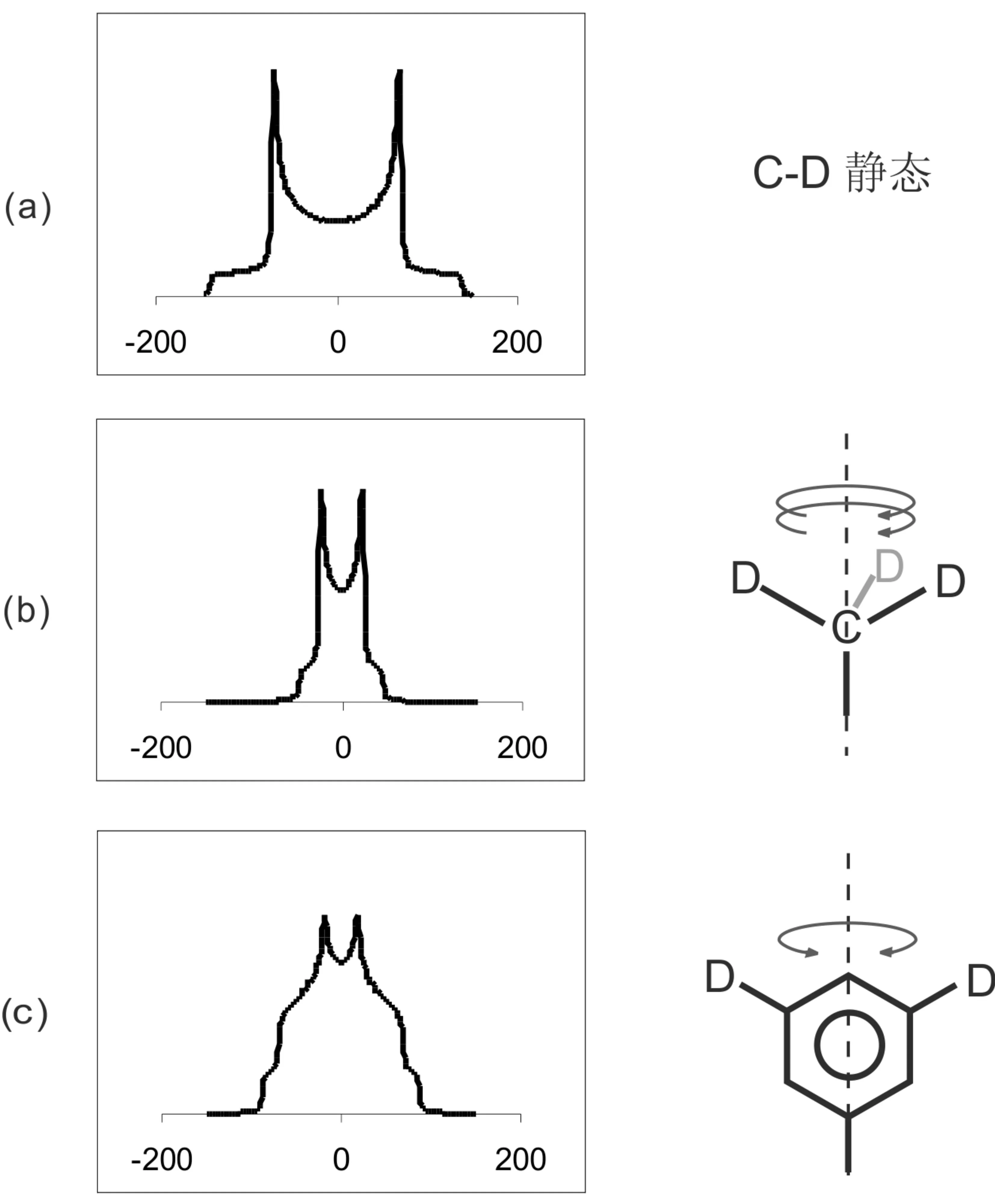
图12　几种运动模式下的2D粉末谱 (a)静态C-D基团；(b)CD3基团快速轴向旋转；(c)苯环180o轴向翻转。

3.4.4交换谱[4]

二维或多维交换谱可以用于表征自相关时间在10-5～102s 范围内的空间运动或化学交换行为，通常以10-3～100s为主。如图13(a)为交换谱实验的基本实验脉冲序列，如果分子链段或基团在tm期间由于取向变化或化学交换而发生了化学位移的改变，则ω1≠ω2，在二维谱图上将会观测到交叉峰；如果分子链段或基团在tm演化期间没有化学位移的改变，在二维谱图上将只能观测到对角峰 (ω1=ω2)。二维交换谱主要研究三种动态行为：(1)分子基团或链段在空间取向或构型的变化；(2)化学交换行为；(3)自旋扩散。此外，改变混合时间tm(图13(b))，可以通过交换谱中交叉峰的有无、强弱或峰形的变化来研究分子基团或高分子链段的空间或化学交换的动力学行为[58,59]。

图13　维交换谱的脉冲序列及谱图示意。 (a)2D NMR交换谱基本脉冲序列；(b)二维各向同性化学位移交换谱。参与化学或空间交换的两种基团的相关峰强度受到混合时间tm的调制。

4总结与展望

随着固体核磁共振硬件和高分辨多脉冲技术的发展，SSNMR谱图的灵敏度和分辨率有了明显的改善。除此之外，偶合重聚技术的灵活应用，使SSNMR在化学材料分子的聚集态、相互作用和动力学方面的应用日趋广泛。然而，多数的高分辨SSNMR技术并不具有普适性，往往十分依赖硬件条件和化学材料本身的性质。这对实验操作者以及实验技术的普及带来了困难。因而如何使固体高分辨NMR技术普适化成为该技术发展的核心之一。此外，SSNMR的实验时间往往较长，常规的一维谱测试可以从一个小时到数小时，甚至数天不等。对于NMR信号较弱的样品，更无法进行多维谱的表征。现今，如何大幅度的提高SSNMR的灵敏度成为了该领域的研究热点。其中，DNP(Dynamic Nuclear Polarization)[60]技术在提高测量灵敏度方面，无论是针对溶液NMR还是SSNMR，都有令人惊叹的表现。现今，商用DNP固体核磁共振波谱仪已经投入生产销售，相信不远的将来，该技术将逐渐走向应用的领域。

参考文献

[1] Mehring M. Principle of High Resolution NMR in Solids,Second Revised and Enlarged Edition. Berlin:Springer-Verlag,1983.

[2] Levitt M H. Spin Dynamics Basic of Nuclear Magnetic Resonance. Chichester, England: John Wiley and Sons Ltd, 2001.

[3] Duer M J. Introduction to Solid-State NMR Spectroscopy. Oxford:Wiley-Blackwell, 2004.

[4] Schmidt-Rohr K, Spiess H W. Multidimensional Solid-State NMR and Polymers. London: Academic Press Ltd,1994.

[5] Ando T, Asakura T. Studies in physical and theoretical chemistry 84: Solid State NMR of Polymers. Amsterdam:Elsevier,1998.

[6] Chan C C. Solid state NMR. Berlin and Heidelberg:Springer-Verlag,2012.

[7] Andrew E R, Bradbury A, Eades R G.Nature,1958,182:1659.

[8] Lowe I J. Phys Rev Lett， 1959, 2: 285-287.

[9] Hartmann S R, Hahn E L. Phys Rev,1962, 128: 2042-2053.

[10] Sarles L R, Cotts R M. Phys Rev， 1958,111: 853-859.

[11] Hodgkinson P.Prog Nucl Mag Res Sp, 2005, 46: 197-222.

[12] Paul S, Kurur N D, Madhu P K. J Magn Reson, 2010, 207: 140.

[13] Lee M, Goldburg W I.Phys Rev,1965,140A: 1261-1271.

[14] Bielecki A, Kolbert A C, Levitt M H.Chem Phys Lett, 1989, 155: 341-346.

[15] Vinogradov E, Madhu P K, Vega S.Chem Phys Lett, 2000, 329: 207-214.

[16] Sakellariou D, Lesage A, Hodgkinson P, Emsley L. Chem Phys Lett, 2000, 319: 253-260.

[17] Elena B, de Paepe G, Emsley L. Chem Phys Lett, 2004, 398: 532-538.

[18] Feike M, Demco D E, Graf R, Gottwald J, Hafner S, Spiess H W.J Magn Reson, series A,1996,122: 214-221.

[19] Lee Y K, Kurur N D, Helmle M, Johannessen O G, Nielsen N C, Levitt M H.Chem Phys Lett, 1995, 242: 304-309.

[20] Carravetta M, Eden M, Zhao X, Brinkmann A, Levitt M H.Chem Phys Lett, 2000, 321: 205-215.

[21] Gullion T, Schaefer J. J Magn Reson, 1989, 81: 196-200.

[22] Liu S F, Mao J D, Rohr K S.J Magn Reson, 2002, 155: 15-28.

[23] Levitt M L. In Encyclopedia of Nuclear Magnetic Resonance, Volume 9: Advances in NMR. Chichester:John Wiley and Sons, 2002, 165.

[24] Schnell I. Prog Nucl Mag Res Sp,2004, 45: 145-207.

[25] Vinogradov E, Madhu P K, Vega S. Chem Phys Lett, 2002, 354: 193-202.

[26] Saalwachter K, Graf R, Spiess H W.J Magn Reson, 2001, 148: 398-418.

[27]Guenes S, Neugebauer H, Sariciftci N S. Chem Rev, 2007, 38: 1324.

[28] Mueller K T, Sun B Q, Chingas G C, Zwanziger J W,Terao Pines T A.J Magn Reson,1990, 86: 470-487.

[29] Chmelka B F, Mueller K T, Pines A.Acc Chem Res,1992, 25: 209-215.

[30] Frydman L, Harwood J S.J Am Chem Soc, 1995, 117: 5367-5368.

[31] Amoureux J P, Trebosc J, Delevoye L, Lafon O, Hu B, Wang Q.Solid State Nucl Mag Res, 2009, 35: 12-18.

[32] Chen J, Shu J, Schobloch S, Kroeger A, Graf R, Munoz-Espi R, Landfester K, Ziener U.Macromole-cules, 2012, 45: 5108-5113.

[33] Shu J, Dudenko D, Esmaeili M, et al.J Am Chem Soc, 2013, 135: 11075-11086.

[34] Robert M W, Tao W. Anal Chem，2001, 73, 4190-4195.

[35] Kurosu H, Chen Q. Annu. Rep NMR Spec, 2004 52: 167-200.

[36] Thierry L, Ludovic L,Christophe V, Jerome M, et al. J Am Chem Soc, 2006,31:10223-10230.

[37] Dudenko D, Kiersnowski A, Shu J, Pisula W, Sebastiani D, Spiess H W, Hansen M R. Angew Chem Int Ed, 2012, 51: 11068-11072.

[38] Niedzialek D, Lemaur V, Dudenko, Shu J, Hansen M R, Andreasen J W, Pisula W, Müllen K, Cornil J, Beljonne D. Adv Mater, 2013, 25: 1939-1947.

[39] Brown S P. Prog Nucl Mag Res Sp, 2007, 50: 199-251.

[40] Schnell I, Spiess H W. J Magn Reson, 2001, 151: 153-227.

[41] Saalwächter K, Lange F, Matyjaszewskix K, Huang C F, Graf R. J Magn Reson, 2011, 212: 204-215.

[42] Zhang Q J, Lin W X, Yang G, Chen Q. J Polym Sci Polym Ed, 2002, 40: 1749-1755.

[43] Lin W X, Bian M H, Yang G, Chen Q.Polymer, 2004, 45: 4939-4941.

[44] Lin W X, Zhang L L, Zhang H P, Chen Q.Acta Polym Sin, 2005, 3: 432-436.

[45] Chen Q, Kurosu H. Annu Rep NMR Spec, 2007, 61: 247-281.

[46] Hou G J, Deng F, Ding S, Fu R Q, Yang J, Ye C H. Chem Phys Lett, 2006, 421: 356-360.

[47] Hou G J, Deng F, Ye C, Ding S. J Chem Phys, 2006, 124: 234512-234700.

[48] Zhang L L, Liu Z J, Chen Q, Hansen E W. Macromolecules, 2007, 40: 5411-5419.

[49] Zhang L L, Chen Q, Hansen E W. Macromol Chem Phys，2005, 206: 246-257.

[50] Shu J, Chen Q, Zhang S M. Chem Phys Lett, 2008, 462: 125-128.

[51] Shu J, Li P, Chen Q, Zhang S M. Macromolecules, 2010, 43: 8993-8996.

[52]Zhao H P, Shu J, Chen Q, Zhang S M. Solid State Nucl Mag Res, 2012, 43-44: 56-61.

[53] Zhang Q J, Chen Q， Yang G， Lin W X.Macromolecules, 2000, 33, 8904-8906.

[54] Hansen M R, Schnitzler T, Pisula W, Graf R, Muellen K, Spiess H W. Angew Chem Int Ed, 2009, 48: 4621-4624.

[55] Hansen M R, Feng X, Macho V, Muellen K, Spiess H W, Floudas G.Phys Rev Lett, 2011, 107: 257801.

[56] Macho V, Brombacher L, Spiess H W. Appl Magn Reson, 2001, 20: 405-432.

[57] Jelinski L W. Ann Rev Mater Sci, 1985. 15: 359-377.

[58] Yang L Y, Wei D X, Xu M, Yao Y F, Chen Q. Angewandte Chemie, 2014, 126: 3705-3709.

[59] Gao Y W, Hu B W, Yao Y F, Chen Q. Chem Eur J, 2011, 17: 8941.

[60] Abraham M, McCausland M A H, Robinsont F N H. Phys Rev Lett, 1959, 2: 449-451.