无诱导信息条件下基于有限理性模糊博弈的车辆路径选择

史国强，周代平，聂化东，闫广聪(重庆交通大学交通运输学院，重庆　400074)



无诱导信息条件下基于有限理性模糊博弈的车辆路径选择

史国强，周代平，聂化东，闫广聪
(重庆交通大学交通运输学院，重庆400074)

摘要:以模糊数学为工具、行为强化理论为基础，建立有限理性模糊博弈的无诱导信息车辆路径选择模型，通过Matlab仿真得出不同初始状态下的博弈平衡结果。结果表明:初始路网交通量的分配比例对路网的平衡状态无显著影响，且当路网交通总量接近路网的通行能力时，博弈结果会达到稳定平衡，当交通量远大于路网通行能力时，博弈结果则呈现峰谷平衡。

关键词:无诱导信息;驾驶员路径选择;模糊数学;博弈论

交通诱导信息作为交通信息的一部分，利用信息对车辆进行诱导，在时间和空间上均衡路网上的交通流，提高路网使用效率［1］。文献［2］在分析系统最优与用户最优各自特点的基础上，建立交通诱导中系统最优与用户最优的博弈协调模型。为提高路网的交通诱导率和通行质量，文献［3］提出基于Stackelberg-Logit博弈的交通诱导模型。文献［4］应用演化博弈论建立诱导条件下驾驶员路径选择行为的演化模型，为制定交通诱导策略提供了理论支持。文献［5］根据诱导系统提供的不同驾驶员的反应行为，建立诱导条件下驾驶员反应行为的博弈模型。以上博弈模型的建立，是以驾驶员完全理性为前提，这与实际并不相符，而且在实际路网中，许多道路上并没有安装交通诱导系统，为此，有必要分析在无诱导信息条件下驾驶员非完全理性的道路交通流的分布情况，以此来指导路网系统发布诱导信息。文献［6－8］提出基于有限理性出行的博弈模型，重点研究最优反应动态学习机制条件下的博弈模型，得出在无诱导信息条件下，有限理性的博弈模型平衡鞍点。最优动态学习机制的基本策略是:驾驶员根据第k次的出行策略来确定自己第k+1次的出行选择。在实际出行中，对驾驶员路径选择影响最大的是近期经验［9］，最优反应动态学习机制以参与博弈的其他局中人策略为学习基础，没有考虑驾驶员自身的驾驶经验和驾驶时间感受。

本文在以驾驶员为有限理性的前提下，综合考虑驾驶员的自身驾驶经验和驾驶时间感受对驾驶员路径选择的影响，利用模糊数学建立有限理性模糊博弈模型，利用Matlab对不同初始状态下的模型博弈平衡结果进行仿真分析。

1模型建立

1．1隶属度函数构造

出行时间是影响路径选择最重要的因素［10］。选择车辆路径时，要考虑到某一路段的时间阻抗，可以根据路阻函数对路段行驶时间进行修正，最常见的路阻函数是美国联邦公路局函数( BPR函数)［11］，其表达式为:式中: t为驾驶员实际驾驶时间; T为自由行驶时(交通量为零)的路段行程时间; c为路段通行能力; q为路段实际交通量;∂、β为路阻函数参数，一般取∂=0．15，β=4。

本文以驾驶员的实际行驶时间来衡量驾驶员选择某条路径所获得的满意程度。如图1所示的简单路网，假设A到B地有L1、L2两条路径，当驾驶员第k+1次选择路径时，则根据第k次的满意度进行选择。满意度是指驾驶员对从A地开往B地所花实际时间的满意程度，是个模糊概念。取论域U=( 0，+∞)，模糊集A1、A2、A3分别表示“满意”、“一般”、“差”(令“满意”=1，“一般”=0，“不满意”=－1，a1为L1路上的满意程度，a2为L2路上的满意程度)，则A1、A2、A3的隶属函数［12］分别为:

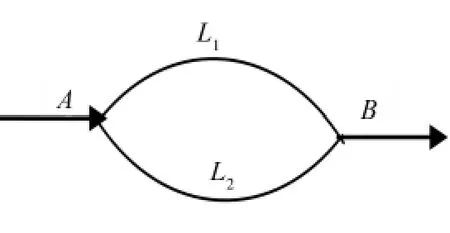
图1简单路网示意图

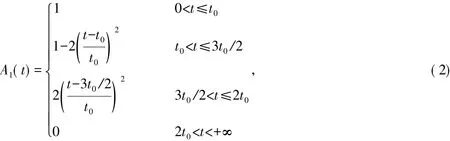
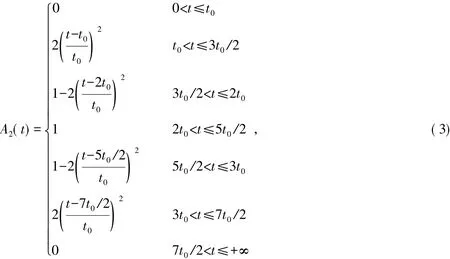
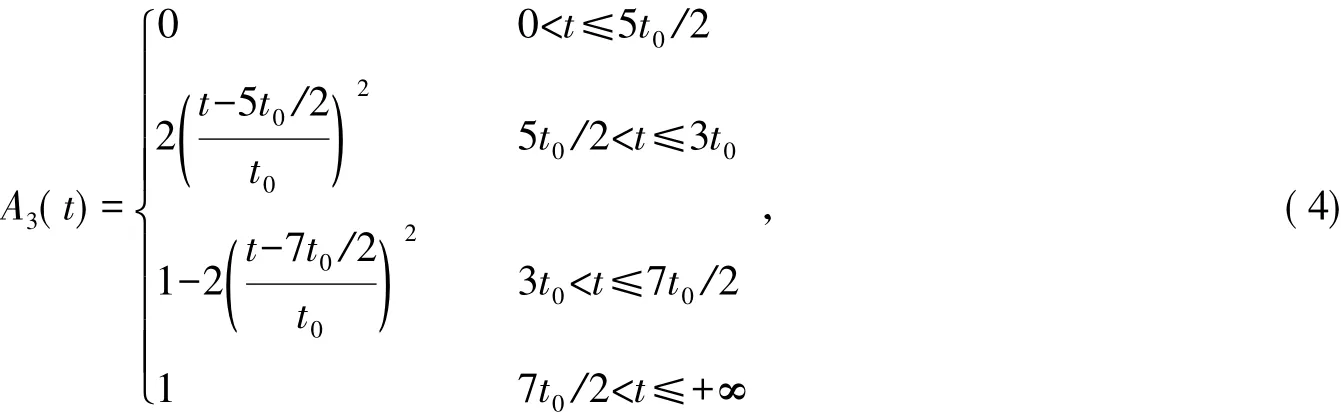
式中: t为驾驶员第k次通过路网L1或L2的行驶时间; t0为驾驶员从A地开往B地的期望时间。

若Max( A1( t)，A2( t)，A3( t) ) = A1( t)，则t∈A1，驾驶员对实际驾驶时间t感觉“满意”;若Max( A1( t)，A2( t)，A3( t) ) = A2( t)，则t∈A2，驾驶员对实际驾驶时间t感觉“一般”;若Max( A1( t1)，A2( t1)，A3( t1) ) = A3( t1)，则t∈A3，驾驶员对实际驾驶时间t感觉“差”。

1．2模型的初始状态

如图1所示，令L1、L2的道路通行能力分别为C1、C2，驾驶员第k次通过L1、L2时的实际交通量为q1，k、q2，k，车辆第k次通过L1、L2到达B地的实际通行时间为t1，k、t2，k。设每次博弈参与的车辆总数Q(假设为标准小汽车)为定值，即q1，k+q2，k=Q，假设博弈时L1、L2路段上均有Q个位置，每辆车在每条路径上都对应1个固定的位置，在L1上占用位置的车辆表示该位置上的车辆上次经过该路段，对应在L2上的位置就空着。每次博弈路径选择按照路段车辆排好的顺序进行，当第k次满意度为满意时，则第k+1次第j位置(忽略L1、L2路段的差异性)上的车辆将会继续选择原路径，即第j位置上的车辆不会跳转到另外一条路径对应的位置上;当第k次满意度为差时，则第k+1次第j位置上的车辆将会选择另外一条路径，即第j位置上的车辆将会跳转到另外一条路径对应的位置上;当第k次满意度为一般时，则第k+1次第j位置上的车辆将会有βj的概率跳转到另外一条路径对应的空位置上( 0≤βj≤1)。

2求解算法

1) h=h+1，v=1，m=0．1，给C1＞C2、βj∈［0，1］，其中m为路径L1上的初始分配比例，h、v为存储记忆的代码。

2)初始化，给出模型的初始状态，Q=q0，q1，0=mQ，q2，0=Q－q1，0。

3)根据式( 1)求得第k次选择路径L1、L2的通过时间t1，k、t2，k。

4)根据式( 2)～( 4)求得t1，k、t2，k的时间感受隶属度，判断驾驶员对第k次路径选择的满意度。

5)由第k次选择的满意度确定第k+1次的选择是否选择其他路径。

①If a1=1，a2=1

L1路径上的车辆继续选择L1，L2路径上的车辆继续选择L2，有: q1，k+1= q1，k，q2，k+1=q2，k。

②If a1=1，a2=0

确定由路径L2上转到L1的车辆，找出路径L1上的所有空位置;将路径L2转出的车辆q2'随机分配到L1的空位置上，确定路径L2的车辆转入到路径L1上的位置。有: q1，k+1=q1，k+ q2'，q2，k+1= q0－q1，k+1。

③If a1=0，a2=1

确定路径L1上转到L2的车辆，找出路径L2上的所有空位置;将路径L1转出的车辆q1'随机分配到L2的空位置上，确定路径L1的车辆转入到路径L2上的位置。有: q2，k+1= q2，k+ q'1，q1，k+1= q0－q2，k+1。

④If a1=0，a2=0

分别确定路径L1转到L2的车辆、L2转到L1的车辆，找出路径L1、L2所有空位置;将路径L1转出的车辆q1″随机分配到L2的空位置上，确定路径L1的车辆转入到路径L2上的位置;将路径L2转出的车辆q2″随机分配到L1的空位置上，确定路径L2的车辆转入到路径L1上的位置。有: q1，k+1=q1，k－q1″+ q2″，q2，k+1=q0－q1，k+1。

⑤If a1=0，a2=－1

确定路径L1转到L2的车辆，找出路径L2上的所有空位置;将L2上的车辆全部转入到L1上，确定路径L2的车辆转入到路径L1上的位置;将路径L1转出的车辆q1'''随机分配到L2的空位置上，确定路径L1的车辆转入到路径L2上的位置。有: q2，k+1=q1'''，q1，k+1= q0－q2，k+1。

⑥If a1=－1，a2=0

确定路径L2上转到L1的车辆，找出路径L1上的所有空位置;将L1上的车辆全部转入到L2上，确定路径L1的车辆转入到路径L2上的位置;将路径L2转出的车辆q2'''随机分配到L1的空位置上，确定路径L2的车辆转入到路径L1上的位置。有: q1，k+1=q2'''，q2，k+1= q0－q1，k+1。

⑦If a1=－1，a2=1

找出路径L2上的所有空位置，将L1上的车辆全部转入到L2上，确定路径L1的车辆转入到路径L2上的位置。有: q1，k+1= 0，q2，k+1=q0。

⑧If a1=1，a2=－1

找出路径L1上的所有空位置，将L2上的车辆全部转入到L1上，确定路径L2的车辆转入到路径L1上的位置。有: q1，k+1= q0，q2，k+1=0。

⑨If a1=－1，a2=－1

找出路径L1、L2上的所有空位置;将L1上的车辆全部转入到L2上，确定路径L1的车辆转入到路径L2上的位置;将L2上的车辆全部转入到L1上，确定L2的车辆转入到路径L1上的位置。有: q1，k+1= q2，k，q2，k+1= q1，k。

6) sumq1，k+1，sumq2，k+1。

7) k=k+1，若k＜100，转3) ;否则，转8)。

8)若m＜1，Z( h，v) = q1，100，m=m+0．1，v=v+1，转2)，否则转9)。

9) q0=q0+Δq，若q0＜2( C1+C2)，转1)，否则结束。

3算例分析

算例中，取C1=1 500 pcu/h，C2=1 000 pcu/h，t0=30 s，q0=1 000辆，βj∈［0，1］，Δq=500辆，路径L1的初始比例m从0依次增加至1。

第99次和第100次的博弈结果如图2所示。

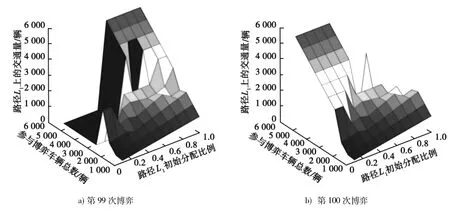
图2不同初始状态下的博弈结果

1)仿真结果表明:

当参与博弈的车辆数Q＜2 500(路网的总通行能力)时，路径L1、L2会达到稳定平衡的状态，路径L1、L2的拥挤程度接近，路网的利用率较高，该状态下路网不需要发布诱导信息。

2)当Q＞2 500，随着Q的增大，路径L1、L2上会呈现峰谷平衡的状态，路网的利用率较低，即参与博弈的车辆数大于路网的通行能力时，要采取相应的管理措施或根据实时路况发布诱导信息，以降低集聚拥堵的现象。

3)当Q一定时，车辆在路径L1、L2不同的初始分配比例，对博弈结果影响不显著。

4　结语

以行为强化理论为基础，利用模糊数学建立有限理性模糊博弈模型，得出各种不同初始状态下的博弈平衡结果。无交通诱导信息的博弈演化过程反映了在自学习机制下，交通量接近路网通行能力时，无诱导也能够达到交通管理者所期望的良好状态。该模型在一定程度上反映了无诱导信息条件下，驾驶员的路径选择规律，对诱导策略制定及其如何制定诱导策略有着一定的指导意义。文章只讨论了在驾驶员期望时间相等时，无诱导信息条件下路网的博弈结果，今后可进一步研究驾驶员期望时间变化时路网的博弈状态，借以指导发布诱导信息。

参考文献:

［1］魏赟，范炳全，韩印，等．交通诱导信息对路网中车辆行为的影响［J］．交通运输工程学报，2009，9( 6) : 114－120．

［2］马寿峰，卜军峰，张安训．交通诱导中系统最优与用户最优的博弈协调［J］．系统工程学报，2005，20( 1) : 30－37．

［3］林娜，王纯．基于Stackelberg-Logit博弈的交通诱导模型［J］．计算机工程与设计，2014，35( 8) : 2841－2845．

［4］李振龙．诱导条件下驾驶员路径选择行为的演化博弈分析［J］．交通运输系统工程与信息，2003，3( 2) : 23－27．

［5］鲁丛林．诱导条件下的驾驶员反应行为的博弈模型［J］．交通运输系统工程与信息，2005，5( 1) : 58－61．

［6］刘建美，马寿峰．基于有限理性的个体出行路径选择进化博弈分析［J］．控制与决策，2009，24( 10) : 1450－1454．

［7］LIU Jianmei，MA Shoufeng．A dimension-reduced method of sensitivity analysis for stochastic user equilibrium assignment model［J］．Applied Mathematical Modelling，2010，34: 325－333．

［8］LIU Jianmei，MA Shoufeng．Algorithms of game models on individual travel behavior［C］．Chengdu: The 8th International IEEE Conference of Chinese logistics and transportation professionals，2008．

［9］刘建美．诱导条件下的路径选择行为及协调方法研究［D］．天津:天津大学，2010．

［10］张杨．不确定环境下城市交通中车辆路径选择研究［D］．成都:西南交通大学，2006．

［11］杨佩坤，钱林波．交通分配中路段行程时间函数研究［J］．同济大学学报(自然科学版)，1994，22( 1) : 41－44．

［12］EREV I，BEREBY-MEYER Y，ROTH A．The effect of adding a constant to allpayoffs: experimental investigation and implications for reinforcement learning models［J］．Journal of Economic Behavior and Organization，1999( 39) : 111－128．

(责任编辑:杨秀红)

Vehicle Routing Choice Based on Bounded Rationality of Fuzzy Game Under No Guide Information

SHI Guoqiang，ZHOU Daiping，NIE Huadong，YAN Guangcong
( School of Transportation，Chongqing Jiaotong University，Chongqing 400074，China)

Abstract:In this paper，fuzzy mathematics is used as the tool and reinforcement theory as the foundation to establish a model of vehicle routing choice with no guide information based on the bounded rational fuzzy game theory and simulate the game equilibrium through matlab under different initial states．The result shows that the initial allocation proportion of the road network traffic has no obvious effect on its balance status．At the same time，when the total network traffic reaches the traffic capacity of road network，the game result will achieve stable equilibrium．When the traffic is far greater than the road network capacity，the game result will reach the peak valley balance．

Key words:no guide information; driver's route choice; fuzzy mathematics; game theory

作者简介:史国强( 1989—)，男，安徽阜阳人，硕士研究生，主要研究方向为交通运输规划与管理．

收稿日期:2015－03－25

DOI:10．3969/j．issn．1672－0032．2015．02．006

文章编号:1672－0032( 2015) 02－0031－05

文献标志码:A

中图分类号:U491．25