基于最小费用最大流算法的冲突车流分配

李　运，潘应久，侯礼兴(长安大学公路学院，陕西西安　710064)



基于最小费用最大流算法的冲突车流分配

李运，潘应久，侯礼兴
(长安大学公路学院，陕西西安710064)

摘要:从最短路径角度研究交通分配问题，利用Dijkstra算法求解最短路径，根据道路容量和运行时间的限制，得出非冲突车流的优化路径，在此基础上假设冲突发生，采用设置优先通行规则与最小费用最大流算法相结合，实现有交通冲突情况下的交通流分配。

关键词:冲突车流;交通分配;最小费用最大流算法; Matlab

交通分配是把各种出行方式的空间O-D( Origin-Destination)分配到具体交通网络上。对于交通分配，国内外均有较多的研究，数学规划法、图论法及计算机技术的发展，为交通分配模型的研制及应用提供了坚实的基础［1］。国际上通常采用平衡和非平衡两大类方法对交通分配进行划分［2］。在交通规划方法相对成熟之后，业内开始把注意力更多的转向交通控制与诱导，由此动态交通分配( Dynamic Traffic Assignment)诞生［3］。

动态交通流分配理论从提出至今经过了20多年的发展，在理论研究和方法应用上都有一定的进步与突破［4］，但仍处于发展阶段，究其根本原因是考虑时间变量因素，建立合适的数学模型并设计相应的算法非常困难［5］。冲突车流分配研究同步于动态分配研究，目前要找到一种解决冲突车流的合适方法仍然是比较困难的。

本文先用Dijkstra算法研究非冲突车流的最短路径，再根据最小费用最大流算法得出非冲突车流的分配并考虑多种情况，最后利用设置优先通行规则与最小费用最大流算法相结合的方法获得冲突车流的分配。

1最小费用最大流算法

最小费用最大流问题是经济学和管理学中的一类典型的基本问题［6］。在一个网络中每条路径都存在“容量”和“费用”两个限制条件，此类问题是想寻找出:车流从A地到B地，选择合适的路径及考虑分配路径的流量，使其能够在流量最大的前提下，达到所用的费用最小的要求。假设n辆卡车要从A地到B地运送物品，由于每条路段都存在不同的收费情况，每条路能容纳的车的数量也有一定限制，最小费用最大流问题指如何分配卡车的出发路径可以使费用降到最低，物品又能准确全部的送达［7］。物流成本最小问题称为最小费用流问题，在现实生活中有很多的应用，一般把其归为一类网络优化问题［8］。可以把容量作为流，费用作为时间代价，来研究交通运输问题。

最小费用最大流算法包含很多经典的算法和流程，本文主要采用其中的最大流算法和最小费用最大流对偶算法。

1．1最大流算法流程

1)对网络G=［V，E，C，W］，给出流值为零的初始流，其中G［V，E］为具有n个顶点、m条弧的有向图，V为n个顶点的非空有限集合，E为m条弧的非空有限集合，C为弧容量，W为弧间的费用函数。

2)作伴随初始流的增流网络G'=［V'，E'，W'］。G'的顶点同G，V' =V(顶点相同)，G'［V'，E'］为增流网络的n个顶点、r条弧的有向图，W'为增流网络间的费用函数。

若G中f( u，ν)＜c( u，ν)，则G'中建边( u，ν)，w'( u，ν) = w( u，ν)。其中: ( u，ν)为顶点，w( u，ν)、w'(ν，u)分别为对应链的费用边权值，f( u，ν)、c( u，ν)分别为可行流的边权值和容量的边权值。

若G中f( u，ν)＞0，则G'中建边(ν，u)，w'(ν，u) =－w( u，ν)。

3)若G'不存在x至y的路径，则G的流即为最小费用最大流，停止计算;否则用标号法( Dijkstra算法)找出x至y的最短路径P。

4)对P的每条边( u，ν)，若G存在( u，ν)，则( u，ν)增流;若G存在(ν，u)，则(ν，u)减流。增(减)流后，应保证对任一边有c( e)≥f( e)≥0。其中: c( e)、f( e)分别为该弧的弧容量和弧流量。

5)根据计算最短路径时的各顶点的标号值L(ν)，修改G所有边的权数w( e)，有L(ν) +w( e)→w( e)。6)将新流视为初始流，转到步骤2)。

1．2最大流最小费用对偶算法流程

1)任意νi∈V，令πi=0;任意(νi，νj)∈E，令fij=0。νi、νj为顶点V集合里的第i和第j个顶点，πi为在i点处构造的弧，fij为ij间的可行流。

2)如果ν0=ν( f)，则f是最小费用流，否则转3)。其中:ν0为最大流的流值，ν( f)为可行流的流值。

3)构造网络G( f，π)，对任意νi∈V，求出G( f，π)中关于wπ的最短且由νs到νi的权d( i)，令πi+di= πi。G( f，π)为以f为顶点、π为弧的有向图，wπ为该链的费用，νs、νt为发点和收点，di为i点对应的距离函数。

4)由新的位势，修改G( f，π)中的费用wπ，再求出G'( f，π)中的最大流。如果最大流的流值为0，则G'( f，π)中不存在由νs到νt的路，停止，且G中不存在流值为ν0的可行流;否则转入步骤5)。

5)沿着最大流确定的由νs到νt的路对f进行增广，且增广后的流值不超过ν0，转入步骤2)［9］。

本文研究交通冲突下路径分配模型，需先研究简单节点路网，由于Dijkstra算法具有计算简单、使用方便等诸多优点，且本文主要研究的路网节点不是很多，所以先采用Dijkstra算法做基本路径;然后考虑节点容量和运行时间对路径的影响，由于最小费用最大流算法能够对有容量限制的路网求解［10］，故选用该算法作为动态路网优化的基本方法。

2非冲突基本路径分配

2．1 Dijkstra算法下最短路径

在非冲突情况下，路段上车流可以按照既定的目标函数找到最短的路径。一般情况下目标函数为实现最短距离、最短时间的函数。图1是一个简单的节点网，各节点的权值为各节点间的距离。求A到F的最短路径，可以用Dijkstra算法计算，其中各节点的权值作为各节点的阻抗。经过计算得出A→F的最短路径为: A →C→D→F。如果为其他目标函数，可以根据各自的目标函数调整节点间的权值，即调整各节点阻抗表，然后进行计算。

2．2考虑路网间运行时间初始流的路径分配

实际情况下路网有容量限制，而且也存在费用的问题，采用最小费用最大流算法进行路径分配。解决最小费用最大流问题，一般有两种方法:

1)先用最大流算法算出最大流，然后根据边费用，检查是否有可能在流量平衡的前提下，通过调整边流量，使总费用得以减少［11］。调整后，得到一个新的最大流，在这个新流的基础上继续检查，调整［12］。这样迭代下去，直至得到最小费用的最大流［13］。这一思路的特点是保持问题的可行性(始终保持最大流)，向最优解推进。

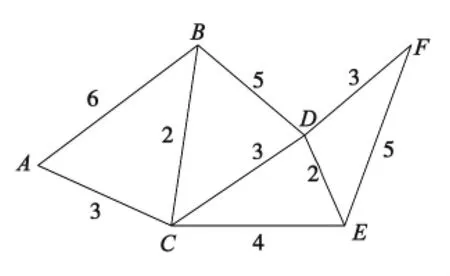
图1简单节点图

2)将零流作为初始流，这个流的费用为零，当然是最小费用。然后寻找一条源点至汇点的增广链，但要求这条增广链必须是全部增广链中费用最小的1条［14］。如果能找出增广链，则在增广链基础上增流，得出新流，将这个流看作初始流，继续寻找增广链增流。这样迭代下去，直至迭代完成，找不到增广链时，这时的流即为最小费用最大流。这一算法的特点是保持解的最优性(每次得到的新流都是费用最小的流)，而逐渐向可行解接近(可行解是最终得到的最大流)。

本文采用第二种方法，先找到不考虑路网间运行时间的初始流，即采用最大流算法找到最优路径，然后根据各节点运行时间来调整这个最大流，从而实现考虑运行时间时的路径分配。

3冲突路径优化分配

交通冲突是在道路可观测条件下，2个或2个以上道路使用者在同一时间、空间上相互接近，如果其中一方采取非常规交通行为，如转换方向、改变车速、突然停车等，除非另一方也相应采取避险行为，否则会发生碰撞［15］，这一现象就是交通冲突。

在交通实际路网中存在很多交通冲突的情况，如何解决这些交通冲突，具有现实意义。在之前的交通流研究中，只是考虑节点容量及运行时间，对于交通冲突没有考虑。根据交通流知识，在产生交通冲突时，应变固定冲突点为随机冲突点，减少冲突次数。制定交通规则时主要考虑整个系统的优化。

1)进入冲突点前，平均速度较大的车流优先通过，道路容量有剩余时其他车流再通过。速度相同时，优先考虑车流大者通行。

2)路途远的车流优先通过，能使其他车流迅速通过，可以减少延误，实现整个系统的优化。

4　算例

4．1路网简介

以浙江大学玉泉校区到紫金港校区的交通路网为例进行研究，该路网包含了拥挤路段、限制路段、畅行路段，在一定程度上代表一个小型路网系统，该路网有21条包含重要交通点的路段，如图2所示。把图2中的21条路段简化为12个节点的路段。节点间的路段长度如图3所示。

4．2 Dijkstra算法下最短路径分配结果

求解图2中节点1→12的非冲突情况下最短路径和最短时间的优化路径。找到最短路径的节点，计算节点1→12的最短路径。

为了简便及具有实际效果，采用Matlab编程模拟Dijkstra算法的过程。根据路段长度，通过Matlab仿真得到节点1→12的最短路径为: 1→2→3→5→8→10→11→12。根据路段长度、路段速度及信号配时，求得节点间的运行时间，得到最短时间的优化路径为1→2→4→7→8→10→12。根据调查数据及Matlab仿真，计算结果如图4所示。

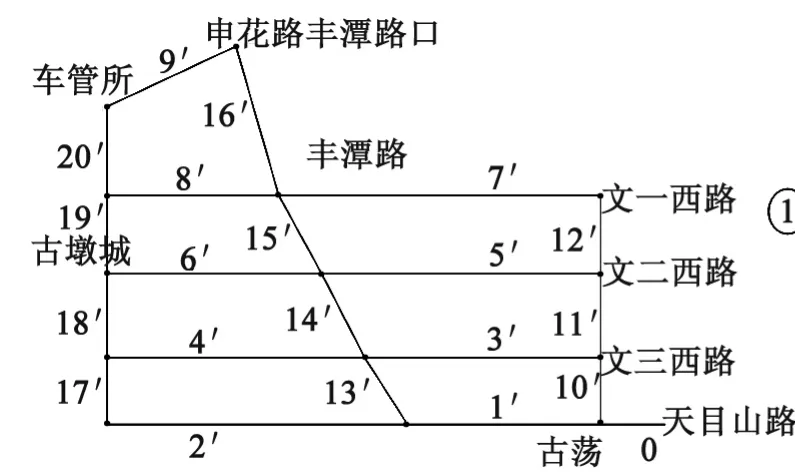
图2简化路段、节点图

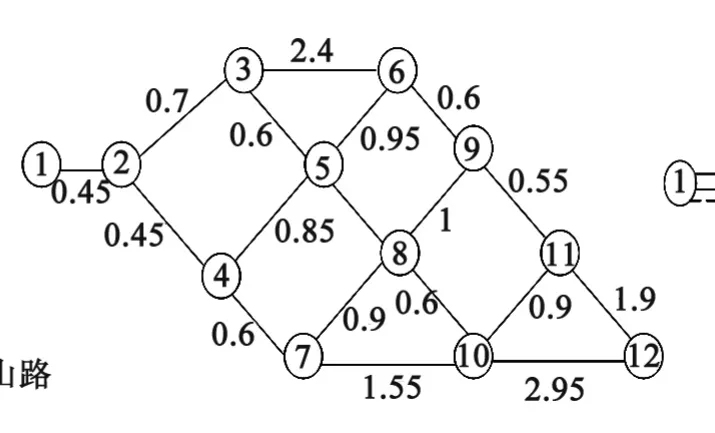
图3节点路段长度图

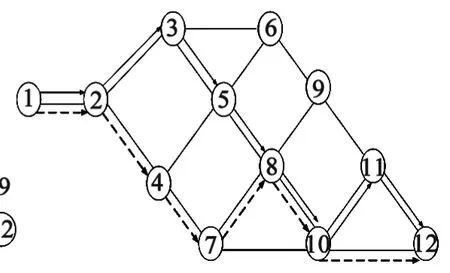
图4基本分配路径

4．3初始流路径分配

在实际情况下需要考虑通行能力、道路情况、交通配时及突发事件应急能力等因素，故引进路段容量参数。路段容量就是路段断面的流量，根据最大通行能力及路段实际情况得到，表1列出了部分路段的容量参数。表1中:ρmax为假设单位密度，pcu/km; q为根据平均速度vp得到的容量，pcu/h，q=ρmaxvp。

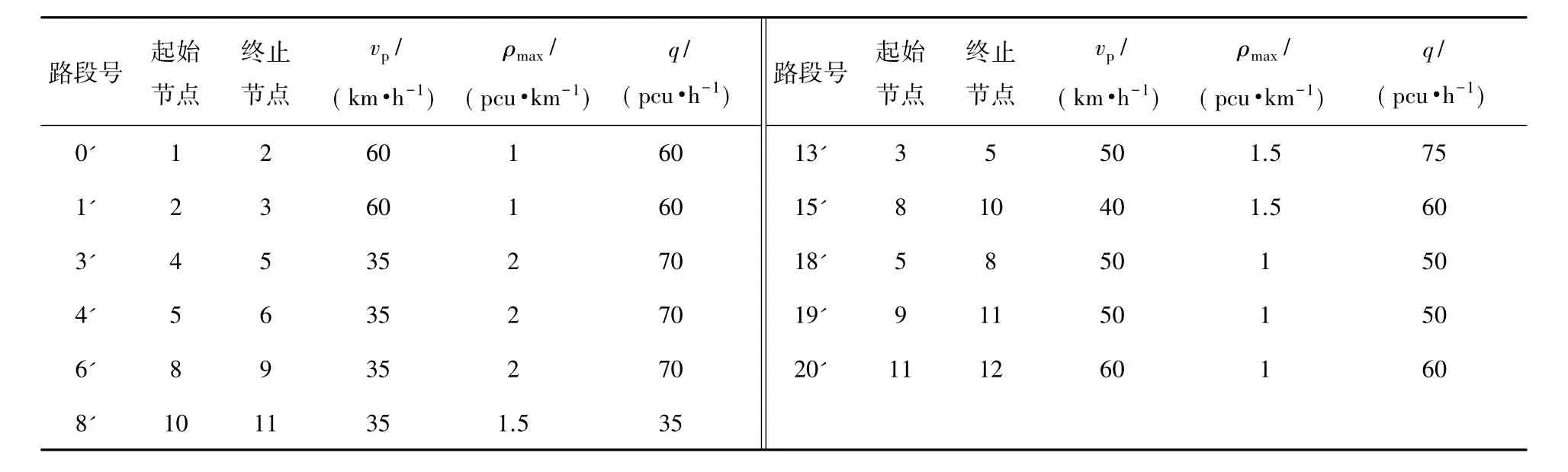
表1部分路段容量参数

本文假设车辆到达是“瞬时、全部”的，例如:节点A→B有100 pcu/h的车流，那么这100 pcu/h的车流只存在A地或B地，而没有处于A地与B地之间的路段上。

解决最大流问题时通常需要一个可行流，选择单车情况下的最短时间路径。假设初始流量为60 pcu/h，因最小时间路径为1→2→4→7→8→10→12，可以发现节点2不能满足道路容量条件，根据最大流算法对初始流进行重新调整，用Matlab编程来实现对偶算法，计算结果如图5所示。由图5可以看出车流在节点2分流，在节点10聚集，能够使车流达到最大，基本与非冲突基本路径中以最短时间为目标函数的路径重合。

4．4考虑路网间运行时间初始流的路径分配

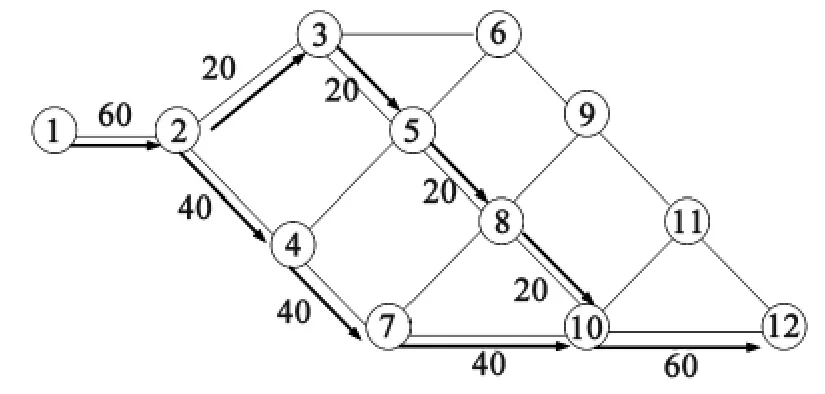
图5初始流分配结果

实际进行初始流路径分配时还要考虑运行时间因素。采用最大流最小费用算法，其中的费用相当于时间代价。考虑路段时间和容量，对于原始的初始流用最大流最小费用算法，采用对偶法找到最大流最小时间。结果表明，60 pcu/h车流在考虑时间和容量的情况下，优化路径和非冲突情况下的最短路径相似，属于非冲突情况下最短时间和最短路径的路径结合，如图6所示。

4．5交通冲突下的车流分配

在实际交通路网中存在很多交通冲突的情况，本文作出一种假设的冲突情况，即由节点1→12的60 pcu/h车流，与从节点3→8的80 pcu/h车流冲突，对两车流的路径进行优化。由于图6的路网是单向图，从节点3→8只有一条唯一路径(可以直观看出节点3→8的最优路径是节点3→5→8)，为了使运算结果准确，须增加节点3→8的路径选择且排除明显会导致运行时间增加的路径，如9以后的节点路段，所以把节点5、6间和8、9间改成双向图。各节点容量如图7所示。

根据速度、容量及在发生冲突下的优先权规则，通过MATLAB编程，得到两种路径及车流分配情况如图8所示。图8中实线代表节点1→12路径，虚线代表节点3→8路径。

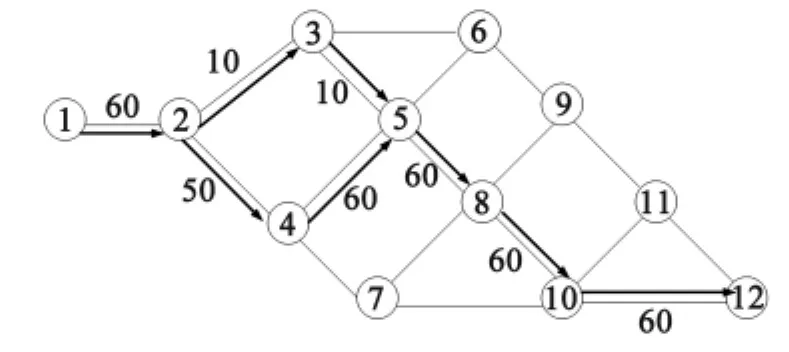
图6考虑各路网间运行时间分配结果

由图8可知，节点1→12和3→8的最优路径在节点3产生了冲突，由于节点2→3的平均速度大于节点3→5的平均速度，优先通过节点1→12的10 pcu/h车流量，于是节点3→5只能走65 pcu/h，剩下的15 pcu/h流量只能走节点3→6。到了节点5，节点4→5有50 pcu/h流量，而节点3→5有75 pcu/h流量，所以优先保证75 pcu/h的流量，50 pcu/h流量不进入节点5，所以节点1→12的50 pcu/h车流走节点4→7。对于混合车流节点3→5的75 pcu/h，到了节点5必须分流，因为节点5→8只有60 pcu/h容量，优先保证路途远的流量，即优先保证节点1→12的10 pcu/h车流量。节点3→8的15 pcu/h车流在节点5走节点5→6。节点1 →12的50 pcu/h车流在节点8与之前的10 pcu/h车流汇合，节点3→8的30 pcu/h( 15+15)车流在节点8与之前的50 pcu/h车流共同到达终点。

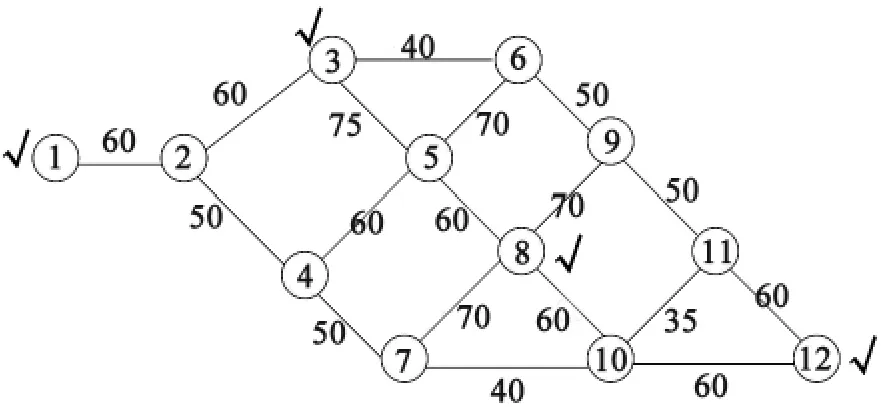
图7交通冲突下的节点容量

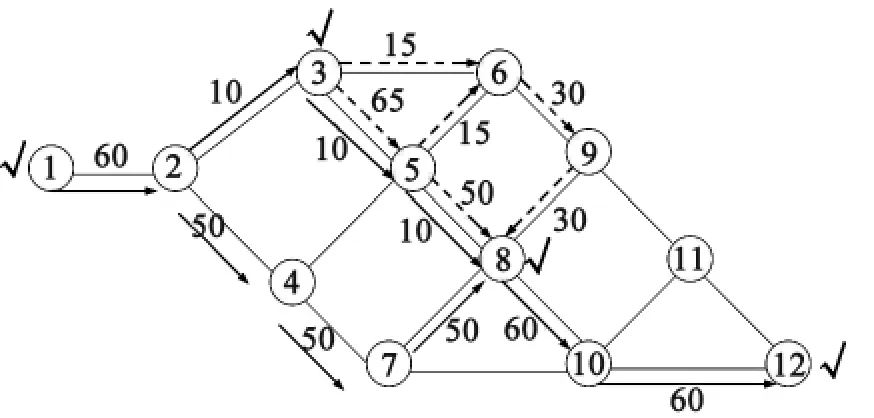
图8交通冲突下的车流分配结果

由图6、8可以看出，节点1→12车流的路径在有无冲突下的主要区别在于其中50 pcu/h这部分车流同另外10 pcu/h车流汇入点的不同，有冲突时避开冲突点(节点5)，选择最近的道路(节点4→7)达到汇合点8，比较符合实际情况，整个车流运行时间变化不大。而相对于节点1→12的路径改变，节点3→8的路径变化就大很多了。为了实现整个路网优化，增加了节点3→8间车流的运行时间，其中主要增加了节点6→9→8( 30 pcu/h)这部分车流的运行时间，但网络优化后车流的运行时间较优化前减少了很多。

5　结语

1)对于简单的、负荷不是很大的交通路网，采用Dijkstra算法进行分配得到基本路径，进而考虑节点运行时间和道路容量进行路径的优化。交通冲突情况下，在最小费用最大流算法基础上，利用计算机编程以及制定通行规则实现算法的优化，从而更好地处理交通流间的冲突。

2)在实际问题中交通冲突情况涉及到的因素很多，具有随机性和复杂性，本文在建模过程中假设冲突车流的到达是“同时、全部”的，但在实际中交通流往往是分时、分段的到达，在接下来的研究中有待于对所建模型进一步完善，以期能更好地提高冲突车流分配结果的准确性。

参考文献:

［1］张维全，张宝玉．公路网规划中多路径交通分配模型的计算机实现［J］．山东交通科技，2005( 4) : 9－13．

［2］黄崇超，刘炳全．非平衡交通分配的几种新的有效分配算法［C］．武汉: 2005—2006年大城市交通高层学术论坛，2006．

［3］杨清华．交通诱导系统的研究［D］．天津:天津大学，2000．

［4］张晓峰，陈鸿杰，王军利．浅析交通分配理论［J］．中国人民公安大学学报(自然科学版)，2007，13( 1) : 91－93．

［5］朱军功．高速公路路网事件的信息发布及救援策略研究［D］．南京:东南大学，2006．

［6］田西，寿建敏，施雄彪．我国货运铁路扩容对煤炭港口吞吐量的影响［J］．中国港口，2011( 5) : 41－44．

［7］沈鑫宇．移动自组网中基于能量的路由协议研究［D］．杭州:浙江工业大学，2011．

［8］张新敬，李刚，邱学绍，等．最小费用最大流算法实现［J］．郑州轻工业学院学报(自然科学版)，2005，20( 3) : 132－134．

［9］白睿．最大流及最小费用研究［D］．南京:南京邮电大学，2012．

［10］吴群妹．受容量限制的多品种物质运输问题的最小费用最大流算法［J］．常州工学院学报，2012，25( 3) : 73－77．

［11］盛鑫芽．ForCES体系结构中流量矩阵建模及其应用的研究［D］．杭州:浙江工商大学，2011．

［12］王勤波．最小费用流问题及其扩展［D］．青岛:青岛大学，2009．

［13］曹志刚．基于网络编码的无线传输优化算法［D］．武汉:华中科技大学，2011．

［14］孟利民，沈鑫宇，周凯，等．基于最小费用最大流的MANET网络路由能量控制模型［J］．传感技术学报，2010，23( 4) : 582－586．

［15］黄娟．信号交叉口通行能力分析及软件设计［D］．南京:东南大学，2006．

(责任编辑:杨秀红)

Research of Conflict-Flow Distribution Based on Minimum-Cost Maximum-Flow Algorithm

LI Yun，PAN Yingjiu，HOU Lixing
( School of Highway，Changan University，Xi'an 710064，China)

Abstract:This article studies the traffic distribution from the angle of the shortest path selection．Firstly，the minimal path can be found out by using the Dijkstra algorithm．Then the non-conflict traffic optimization path is obtained on the basis of road capacity and the limitation of operation．Finally，under the condition of this conflict assumption，it concludes that the goal of the trip distribution in traffic conflict situations can be achieved by setting priority rules and minimum cost maximum flow algorithm．

Key words:conflict-flow; traffic distribution; minimum-cost maximum-flow algorithm; Matlab

作者简介:李运( 1990—)，男，内蒙古包头人，硕士研究生，主要研究方向为交通规划及交通政策．

收稿日期:2015－03－31

DOI:10．3969/j．issn．1672－0032．2015．02．005

文章编号:1672－0032( 2015) 02－0025－06

文献标志码:A

中图分类号:U491．2