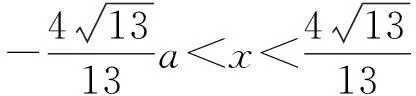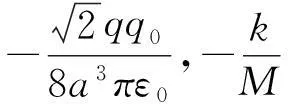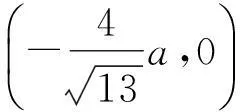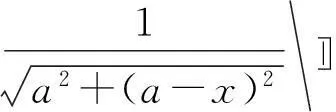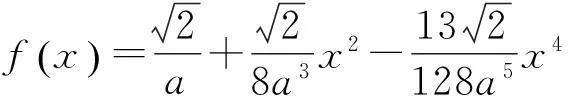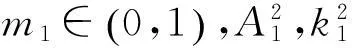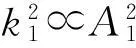带电粒子在四电荷系统内的运动模型及其应用

带电粒子在四电荷系统内的运动模型及其应用

徐 斌陈 浩②

(华南师范大学物理与电信工程学院广东 广州510006)

指导教师：陈浩(1959-)，男，教授，硕士生导师，博士，主研方向为理论物理，包括非线性物理、量子场论和凝聚态物理等前沿领域以及理论物理的教学研究.

摘 要：以对称分布的四电荷系统为例，研究任意带电粒子在对称的电场分布内的运动性质，借助椭圆函数和积分的方法分别推导出粒子的运动学方程，探讨了该类运动模型在求解物理问题时的应用.

关键词：四电荷系统对称电场分布物理教学

作者简介：徐斌(1991-)，男，在读硕士研究生，主研方向为物理课堂教学、国外物理教材分析.

收稿日期：(2015-05-13)

1引言

大学物理静电场的教学中重点讨论过单个点电荷及电偶极子等带电系统的电场分布[1].任意带电粒子在对称的电场分布内运动的模型在以往的教学中并不常见，然而这种模型的很多性质可用于大学物理课堂教学中.本文以四电荷系统为例，从能量角度出发具体分析了四电荷系统的性质，对不同初始能量的任意带电粒子在电场中的运动进行定量分析，在对电势分布作不同的近似后，采用两种方法推导出运动学方程，分别分析了任意带电粒子在系统中运动的线性和非线性性质，并重点介绍了该体系在物理教学中的应用.

2模型的介绍

如图1所示，边长均为2a的矩形的4个顶点固定4个等量同号的点电荷，讨论与场源电荷异号的任意带电粒子在对称轴线(以下讨论以x轴为例)上的运动情况[2].

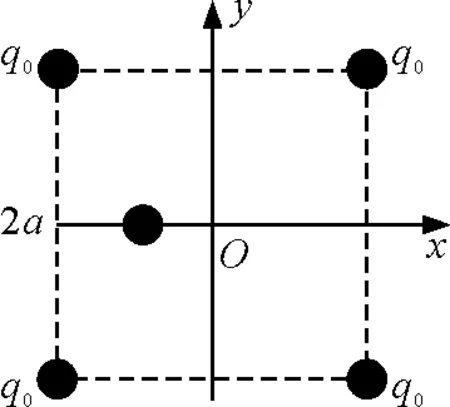
图1　四电荷模型示意图

建立如图1所示的坐标系，设点电荷的电荷量为q0，运动带电粒子的电荷量为-q，可以得出带电粒子在x轴上的电势能分布方程[3]

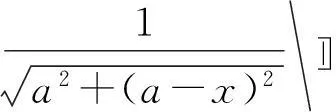
(1)

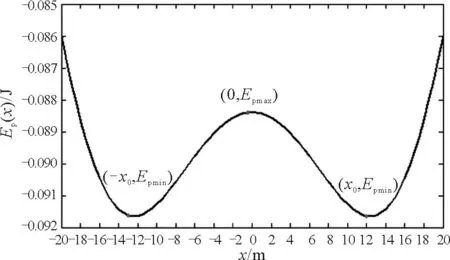
图2　 E p( x)- x图

3模型在物理教学中的应用分析

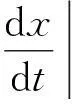
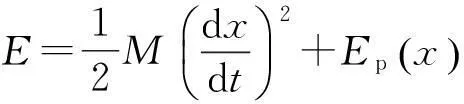
(2)

结合图2及给定的总能量E对带电粒子的运动情况定性分析.

3.1模型一般性质的分析

当E=Epmax时，带电粒子静止在势垒上，但此时的静止状态是一个亚平衡态，如果给一个沿x轴的微小扰动它将离开亚平衡位置做大振动.当E=Epmin时，运动电荷静止在势阱处，此时为平衡态，如果给一个沿x轴的微小扰动它将离开平衡位置做小振动.当E>0时，由于运动电荷的电势能总是小于零，可见速度v不可能为零，所以此时运动电荷必定一直运动至无穷远，和天体物理中动能大于引力势能时即可发射一颗卫星离开行星的情况一样，此时带电粒子的能量超过电势能分布的最高能量，将不受电场束缚，运动到无穷远处.当Epmax

3.2模型的教学意义分析

3.2.1线性振动的研究

(3)

对式(3)右边作泰勒展开,忽略4次及以上项,得

(4)

则带电粒子的动力学方程为

F=-

(5)

x=Asin(ωt+φ)

(6)

可见,带电粒子在这种情况下的运动模型非常类似于量子场论中对称性自发破缺的例子.因此,我们可以把Epmax看作是体系对称性破缺的临界能量,Epmin则为基态能量,当带电粒子处在基态能量与临界能量的范围内时,它的运动情况发生了对称性破缺,其解只能是任意一个,而它们都不具有哈密顿量的坐标反演不变对称性,而当带电粒子的能量高于临界能量时,它的运动情况只有一种,其解具有与哈密顿量相同的坐标反演不变对称,这时候系统的对称性没有遭到破坏[4].

在经典力学中存在不少对称性破缺的例子,一般和能量的取值有关.比如一支铅笔垂直静止放置时的重心很高，重力势能较大，此时系统是关于沿铅笔头、尾所在的直线轴对称的.而一旦给铅笔一个微扰后，铅笔会倒下来，此时能量降低了，但是轴对称性亦被破坏了.本系统也不例外,我们看到,当能量降低到一定程度(到达临界能量)时,就会出现对称性破缺.故本文所讨论的系统有助于形象地理解场论中关于自发对称性破缺的模型[5].

3.2.2非线性振动的研究

结合式(1)、(2)得

(7)

(8)

对式(8)作泰勒展开,忽略6次及以上项,得

(9)

则式(7)可化简为

(10)

借助椭圆函数解法，可求出带电粒子的运动学方程[4]

x=A1dn[k1(t-t1),m1]

(11)

(12)

(13)

(14)

令k1>0,则

4结语

本文所研究的运动模型有助于学生理解场论中的对称性破缺概念，在非线性教学中，同样有辅助教学的作用，因此该模型可以作为大学物理教学中的一个例子.四电荷系统只是对称电荷系统中的一个特例，其他对称分布电场的性质也是类似的，本文的研究方法和视角对研究其他对称分布有一定的借鉴意义.

参 考 文 献

1赵凯华，陈熙谋．新概念物理教程 电磁学(第2版)．北京：高等教育出版社，2006.1～42

2孙晓林，董慎行．带电粒子在四电荷点阵中的运动.物理与工程，2005，5(15)：12～16

3刘式适，刘式达．物理学中的非线性方程(第2版)．北京：北京大学出版社，2012.59～61

4戴元本．相互作用的规范理论(第2版)．北京：科学出版社，2005.35～46

5J. Goldstone， A. Salam and S. Weinberg. Broken Symmetries.Phys. Rev. 1962，127(3)： 965～970

The Charged Particle′s Motion Model and

Its Application in a Four-charge System

Xu BinChen Hao

(School of Physics and Telecommunication Engineering， South China Normal University， Guangzhou，Guangdong510006)

Abstract:In the case of the four-charge system,the vibrations of charged particles in symmetrical distribution of the electric field are investigated.With the elliptic function and integral technique,the kinematics equation of particle is presented,respectively.The model investigated in this paper can help students understand spontaneous symmetry breaking and nonlinear physical knowledge in college physics teaching.

Key words:four-charge system; symmetrical distribution of the electric field; physics teaching