物理实验数据处理中线性函数逐差法与平均法的关系

何述平

(西北师范大学教育学院物理教育研究所　甘肃 兰州　730070)

物理实验数据处理中线性函数逐差法与平均法的关系

何述平

(西北师范大学教育学院物理教育研究所甘肃 兰州730070)

摘 要：探究了物理实验数据处理中线性函数逐差法与平均法的关系问题，给出了细致的推证，结果表明：线性函数逐差法与平均法等效．

关键词：线性函数逐差法平均法关系

1引言

物理实验数据处理中时常遇到两个直接测量量呈线性函数关系，因此，探究线性函数的数据处理方法具有现实意义．线性函数的数据处理基本方法(准确程度由低到高)有：图像法、平均法、逐差法、最小二乘法，且分别有所论述[1]．然而，线性函数逐差法与平均法有无关联？若有，具体怎样？本文就此进行相应的探究，以明确线性函数逐差法与平均法的关系，并为进一步理解与运用逐差法或平均法进行线性函数的数据处理奠定理论基础．

2探究

逐差法、平均法是物理实验数据处理的基本方法，也是解决拟合(回归)直线时方程数多于变量数的方法[1]；据此简明、普遍推证线性函数的逐差法、平均法，进而明确其关系．设物理直接测量量x和y呈线性关系

y=a0+a1x

(1)

式中a0与a1为间接测量量(恒量)．测2n组数据(xi,yi)，i=1,2,…,2n，n≥1；依次代入式(1)，得2n个线性方程．

2.1线性函数逐差法

根据逐差法处理数据的基本思想[1]，式(1)的2n个线性方程按测量数据大小顺序隔n项逐差，得

yi+n-yi=a1(xi+n-xi)

(2)

式(2)求和，得

(3)

式(1)的2n个线性方程求和，得

(4)

式(3)代入式(4)，化简得

(5)

简化式(5)、(3)，有

(6)

(7)

2.2线性函数平均法

根据平均法处理数据的基本思想[1]，式(1)的2n个线性方程按测量数据大小顺序对半分为两组，再分别求和，得

(8)

(9)

由式(8)、(9)得

(10)

(11)

简化式(10)、(11)，有

(12)

(13)

2.3线性函数逐差法与平均法的关系

比较式(12)、(13)与式(6)、(7)知：线性函数逐差法、平均法的表达式相同，即对同一2n组直接测量量(xi,yi)，线性函数的a0与a1(间接测量量)的逐差法、平均法的估值相同；且有数据处理实例[1]表明线性函数逐差法、平均法对同一2n组数据给出相同的结果．因此，线性函数逐差法、平均法的效果相同，即等效．可谓异曲同工．

3讨论

3.1特点

由上述推证可见：逐差法的实质是差分-平均，平均法的实质是分组-平均[1]；因此，线性函数逐差法、平均法的等效反映间接测量量对直接测量量取平均的效果[式(12)、(13)]，只是这种平均是粗略的统计平均，而非准确的统计平均(如线性函数最小二乘法)，即线性函数逐差法、平均法的等效实质是粗略的统计平均，并非某种运算巧合．

逐差法的适用条件是因变量与自变量的函数形式为多项式和自变量等间距变化[1]，因此，线性函数逐差法，若对自变量有等间距的条件，则为严格的逐差法；若无此条件，则为广义的逐差法即差值法[1]．对式(1)线性函数逐差法、平均法，都要求测2n组即偶数组数据，因需同时确定两个间接测量量a0与a1．

对式(1)的线性函数，最小二乘法的估值为[1，2]

(14)

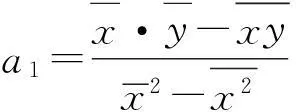
(15)

比较式(14)、(15)与式(12)、(13)知：线性函数逐差法、平均法的表达式与最小二乘法的不同，即对同一2n组数据，逐差法、平均法处理的结果一般与最小二乘法的不同．然而，线性函数最小二乘法却要求自变量无测量误差、仅因变量有测量误差或自变量的误差限相对较小或可忽略[1，2]，且无偶数组数据的要求．

线性函数的逐差法、平均法与最小二乘法不同，但线性函数逐差法、平均法处理数据的结果与线性函数最小二乘法的却很接近[1]；线性函数逐差法、平均法的等效实质是粗略的统计平均，因粗略而计算标准差或不确定度就没有多大的意义[1]．因此，线性函数逐差法、平均法不失为简便、实用的中学物理实验数据处理的基本方法．

3.2建议

鉴于线性函数逐差法与平均法等效，因此，中学物理实验中涉及线性函数的数据处理，既可运用逐差法，又可运用平均法(当然可运用最小二乘法)．尤其对普通高中课程标准实验教科书中涉及的基本而重要的实验(如测自由落体的加速度[3]、测电源的电动势和内阻[4])，应运用线性函数逐差法或平均法处理数据，而不仅仅是运用更粗略的作图图像法(当然可运用准确的回归图像法[5])．

4结语

本文细致推证了物理实验数据处理中线性函数逐差法与平均法的等效；讨论了线性函数逐差法与平均法的等效实质、各自特点，线性函数逐差法与平均法不等效的特例及其特点，并与线性函数最小二乘法做了比较；提出了运用线性函数逐差法与平均法处理数据的建议．

本文的探究深化了线性函数逐差法与平均法的认识，奠定了合理运用线性函数逐差法或平均法处理数据的理论基础．

参 考 文 献

1龚镇雄．普通物理实验中的数据处理．西安：西北电讯工程学院出版社，1985．67～168，132，119～120，126～127，120～121，134～135，130

2朱鹤年．基础物理实验教程：物理测量的数据处理与实验设计．北京：高等教育出版社，2003．67

3人民教育出版社课程教材研究所，物理课程教材研究开发中心．普通高中课程标准实验教科书物理1(第3版)．北京：人民教育出版社，2010．44

4人民教育出版社课程教材研究所，物理课程教材研究开发中心．普通高中课程标准实验教科书物理选修3-1(第2版)．北京：人民教育出版社，2007．69～70

5何述平．图像法处理打点纸带的研究．物理教师，2013，34(1)：57～60

The Relation between Successive Difference Method

and Average Method of Linear Function

in the Physical Experiment Data Processing

He Shuping

(Research Institute of Physics Education，College of Education，Northwest Normal University，Lanzhou,Gansu730070)

Abstract：This paper inquires into the relation between equaling difference method and average method of linear function in the physical experiment data processing，particular deductions are given，the results indicate that equaling difference method and average method of linear function are equivalent；and necessary discussion is made．

Key words：linear function；equaling difference method；average method；relation

收稿日期：(2015-03-30)

作者简介：何述平(1964-)，男，硕士，副教授，从事物理教学论的理论和实验的教学与研究工作．