基于动力非线性有限元法的索-梁相关振动研究

第一作者王涛男，博士生，1983年8月生

通信作者沈锐利男，博士，博士生导师，1963年7月生

基于动力非线性有限元法的索-梁相关振动研究

王涛，沈锐利

(西南交通大学土木工程学院桥梁系，成都610031)

摘要：根据考虑结构几何非线性的有限元动力时程积分算法，开发了有限元程序SD_FEM。使用该程序建立了精细的索-梁组合结构有限元模型，计算了结构的自振特性与结构在外部动力荷载作用下的振动响应。分别讨论了当整体结构自振频率与拉索局部自振频率有1∶1、2∶1和不成倍数关系时，索-梁相关振动导致拉索振动的状况。分析了数值计算结果，总结了索-梁相关振动的本质规律。

关键词：拉索；振动；动力特性；几何非线性；有限元方法

基金项目：国家自然科学基金资助项目(51178396)

收稿日期：2014-01-08修改稿收到日期：2014-05-29

中图分类号:TU317文献标志码：A

Cable-beam vibration study with nonlinear dynamic FEM

WANGTao,SHENRui-li(School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract:A nonlinear FEM program named SD-FEM was developed based on the FE dynamic time history integral algorithm considering geometric nonlinearity. A micromesh FE model for a cable-beam structure was built by using the program, its natural vibration characteristics and its vibration response under external dynamic loading were calculated. The situations of local cable vibration caused by cable-beam vibration were discussed when the ratio of the global natural frequency of the model to the natural frequency of cable was 1∶1, 2∶1 and not a multiple, respectively. The numeric calculation results were analyzed, and the essential rules of cable-beam vibration were summarized.

Key words:cable; vibration; dynamic character; geometrical nonlinearity; FEM

斜拉桥拉索在端部位移激励下的大幅振动现象是国内外较为关注的研究课题。Max Irine[1]在其著作中较为详尽地讨论了索结构的静力与动力理论。Nayfeh[2]在其研究著作中通过理论方法详细地论述了非线性振动的各种重要性质。汪圣刚[3-6]分别建立并完善了拉索在端点位移作用下发生大幅振动的理论计算模型，对拉索在端点位移激励下振动的机理与振动特性进行了详细研究与讨论。De Sá Caetano[7]在其研究著作中对拉索振动的理论方法做了较为全面的总结。Gattullia[8-9]分别使用了更为精细的理论方法、数值计算方法，讨论了索-梁组合结构在端点位移激励作用下的振动特性。陈丕华等[10]针对单根拉索在端点位移作用下的振动特性进行了试验研究。

目前业界的研究表明，对于斜拉桥这样一个复杂的索、梁组合结构，拉索与整体结构的振动往往是互相影响的。

王涛等[11]将索-梁组合结构中拉索在端点位移激励作用下的振动定义为索-梁相关振动，基于拉索的非线性振动方程开发了“索动力单元”，该单元在静力计算时为普通的杆单元，在动力特性计算中可以根据拉索轴力计算拉索的各阶自振频率，在动力时程计算过程中根据拉索理论振动方程计算拉索的动拉力对整体结构的作用，将拉索局部振动与整体结构振动整合在了一起，计算了索-梁组合结构自由振动的特性，较为合理的讨论了拉索局部振动与整体结构振动的关系。

为了在动力时程计算中更好地模拟结构的动态受力情况，在本文研究中，以考虑结构几何非线性的有限元动力时程积分算法为基础，开发了有限元程序，构建了精细的索-梁组合结构有限元模型，根据非线性振动力理论原理，分析了计算结果，总结了索-梁相关振动的规律。

1非线性有限元动力时程积分

1.1基本理论

若要完全考虑结构的几何非线性，则必须在动力时程积分的每一步中使用平衡迭代。本文使用的非线性Newmak-β法的基本假定与普通的Newmak-β法相同，可以写为：

(1a)

(1b)

其中各个参数表达式可以参见文献[12]。与线性计算方法不同，考虑几何非线性时，有限元结构t+Δt时刻的振动方程为：

Δ t)}+{ R({ δ( t+Δ t)})}=

(2)

将式(1)代入式(2)，可以得到：

(a0[M]+a1[C]){δ(t+Δt)}+{R({δ(t+Δt)})}=

{F({δ(t+Δt)})}+{Fe({δ(t+Δt)})}+

(3)

这样，有限元动力时程积分问题就转化为在每一个时间步求解非线性方程组(3)的问题。

可以使用牛顿迭代法来求解式(3)。式(3)左端中结构振动的恢复力向量{R}是节点位移向量{δ}的非线性函数。对于{R}本文使用的计算方法与有限元CR列式静力计算方法相同，即：对于杆单元通过节点的伸长来计算杆件承受的真实轴力，对于梁单元不仅要计算导致伸长承受的轴力，还要扣除单元刚体转动后的计算节点转动值来得到单元承受的实际弯矩。利用杆端位移计算杆端力的公式与计算方法详见文献[12-13]，但文献中主要关注结构静力计算问题。

在考虑结构几何非线性时，式(3)右端结构承受的外力向量{F}与结构初始力导致的等效外力向量{Fe}(如：ANSYS中初应变的概念)也是位移{δ}的非线性函数。它们都需要通过当前迭代步的单元坐标转换矩阵来计算。

当迭代未收敛时，式(3)左右两端是不相等的，计算式(3)两端的差值就可以得到迭代不平衡力。迭代过程中使用的切线刚度矩阵为等效总体刚度矩阵：

[K]=a0[M]+a1[C]+[K0]

(4)

式中:[M],[C],[K0]分别为将节点坐标更新到当前迭代步位置上时，结构的总体质量矩阵、总体阻尼矩阵、静力计算的总体切线刚度矩阵。

1.2算法流程

综上所述，本文中考虑几何非线性有限元动力时程积分Newmak-β法大致计算流程如下：

图1　非线性有限元法计算流程图 Fig.1Calculation flow graph of Nonlinear FEM

根据以上所述计算原理，本文编制了非线性静/动力计算程序SD_FEM。为了体现问题的本质，同时简化模型，提高计算效率，研究中使用了2维的平面有限元模型。关于3维空间杆系结构有限元动力时程计算方法思路与图1是相同的，只是单元坐标变换与结构非线性振动恢复力的计算更为复杂。

1.3算例验证

计算某根拉索(如图2所示)自重构型下，在右端点Y方向位移激励作用下发生大幅振动的情况。

图2　拉索有限元模型图 Fig.2 FEM model of the Cable

设拉索有限元模型的各个参数为：拉索两端点距离为l=100 m；弹性模量E=2.01e11 Pa；拉索初始轴力H=1 080 kN；截面面积A=0.006 m2；材料质量密度ρ=8 000 kg/m3；重力加速度G=9.8 m/s2。

首先使用本文程序建立图2中的拉索有限元模型，拉索共分为10个直杆单元，考虑几何非线性计算拉索的静力构型后，计算拉索的动力特性得到拉索模态如图3所示。

图3　拉索振动模态 Fig.3 Vibration modes of the Cable

设图2中ΔUY=UYsin(ωt)，根据动力特性计算结果，这里取端点位移激励频率为0.835 Hz，UY=0.1 m。算例中不考虑阻尼，分别使用ANSYS(使用link1单元)与SD_FEM计算，使用强制位移施加端点位移激励，取动力时程计算时间步长Δt=0.02 s(在ANSYS与本文程序中都使用固定时间步长)，共计算1 500步，得到拉索的1/2点振动时程曲线如图4所示。

图4　拉索1/2点振动时程 Fig.4 Vibration time history curves of the 1/2 point of the Cable

观察图4 ，可以看出，本文程序SD_FEM非线性动力时程计算结果与ANSYS结果几乎没有差别，这说明了本文程序的正确性与可靠性。由于SD_FEM是杆系结构专用程序，计算速度较快，在本文作者计算机上，完成1 500步的计算用时约为12 s，而ANSYS用时约为3.5分钟。本文程序计算速度较快，且提取、整理计算结果都相对较为方便。

2索-梁相关振动特性研究

在本节中，基于文献[11]中的算例，使用本文程序进一步研究索-梁相关振动的特性。

2.1计算模型

文献[11]中模型如图4所示。梁为4个平面梁单元(①~④)，拉索为3个可以考虑拉索非线性振动效应的直杆单元(⑤~⑦)。节点1,6,7,8完全约束。

图5　结构有限元模型 Fig.5 Global FEM model of the structure

对于图4中的拉索，文献[11]中定义了索-梁相关振动的概念，它容易导致拉索的大幅振动包括[3,4,6,8]：

主共振：当拉索端点位移激励沿Y1方向分量的频率与拉索的自振频率比接近1∶1时拉索发生的强迫激励作用下的大幅振动。

参数共振：当拉索端点位移激励的X1方向分量频率与拉索的自振频率比接近2∶1时，拉索发生的参数激励作用下的大幅振动。

本文中，使用SD_FEM程序建立更为精细的有限元离散模型，如图5所示。

图6　结构有限元模型 Fig.6 Global FEM model of the structure

这里还是按照图4 中的惯例，将结构上的拉索称为⑤,⑥,⑦号拉索。拉索⑤较长，分为12个直杆单元；⑥,⑦号拉索都分为10个直杆单元，各个拉索中点节点编号分别为14,24,33，拉索⑤的1/4点编号为11。

2.2频率比1∶1时结构索-梁相关振动特性

取重力加速度G=9.8 m/s2，设置图4中模型各个构件的参数如表2中所示。

表1　结构参数

按表1参数，考虑几何非线性，计算得到图4有限元模型在自重作用下的静力构型，拉索⑤,⑥,⑦的轴力分别为3.143e6 N, 3.011e6 N, 2.962e6 N，根据考虑垂度的拉索自振频率理论公式计算[11]，得到各拉索1阶自振频率分别为0.958 Hz, 1.434 Hz, 2.606 Hz。计算图4有限元模型在自重静力构型下的动力特性，得到整体结构模态如图6所示。

图6　结构振型图 Fig.6 Vibration modes of the structure

可以看出，整体结构的1阶自振频率与拉索⑤的1阶自振频率比例关系接近1∶1。

按表1参数，建立图5有限元模型，考虑几何非线性计算结构在自重下静力构型，再计算结构动力特性如图7所示。

图7　结构振型图 Fig.7 Vibration modes of the structure

可以看出，如果使用图4有限元模型，通过有限元模型求出整体结构的振动特性，使用解析公式计算拉索的自振频率，可以较为容易的分辨、对比拉索的局部自振频率与整体结构自振频率。使用图5有限元模型，拉索的局部振型与整体结构的振型是“混合”在一起的，相对较为不容易分辨。观察图6与图7也可以发现，这两种方式是可以对比验证的。

为了考察模型的非线性振动特性，使用图5有限元模型，在计算结构的静力构型后，在节点5上施加沿Y0方向的动态力P0sin(ωt)。取动态力频率在0~3.0 Hz范围内变化，P0=-30 000 N。不虑结构阻尼，动力时程计算时间步长取为0.02 s，每个时间点计算5 000步。提取各个时间点节点 5沿Y0方向，拉索⑤,⑥,⑦中点(节点14,24,33)沿Y1方向的最大响应，绘制节点频率-响应曲线如图8所示。

图8　有限元模型各个节点的频率-响应曲线 Fig.8 Thefrequency-response curve of the nodes of FEM model

从图8中可以看出，当外激励频率在约0.9 Hz到1.0 Hz 范围内时，外激励频率接近整体结构与拉索⑤的1阶频率，整体结构在外激励作用发生了共振。由于整体结构1阶自振频率与拉索1阶自振频率接近1∶1的关系，拉索⑤(1/2节点14)在端点位移的带动下发生了1∶1的主共振，振动幅值较大。且频率-响应曲线有向右弯曲的趋势，体现了“硬弹簧”的性质。

当外激励值在其它拉索自振频率附近时，由于整体结构响应较小，拉索端点位移激励幅值较小，拉索振幅较小。当外激励频率远离拉索与整体结构的自振频率时，结构的响应都相对很小。

为了研究拉索在索-梁相关振动作用下发生主共振的特性，使用图5有限元模型，在计算结构的静力构型后，在节点5上，沿Y0方向施加动态力P0sin(ωt)，设动态力频率为0.96 Hz,P0=-30 000 N。计算时间步长取为0.02 s，共计算10 000步。

非线性动力时程计算非线性Newmak-β法中设置γ=0.505，相当于施加了较小的算法阻尼，(经过本文试算，这个阻尼的量级大约相当于有限元模型中Rayleigh阻尼[C]=α[M]+β[K]中分别取[M]与[K]为建模初始值，α与β均取为2.0e-4时的阻尼值)。

动态力频率接近整体结构的1阶自振频率，会造成整体结构的共振。首先，提取节点14的在Y1方向的振动时程曲线如图9所示。

图9　节点14振动时程图、频谱图 Fig.9 Vibration time history and Spectrogram curve of node 14

从图9中可以看出，在外激励作用下，索-梁相关振动导致了拉索⑤(1/2节点14)发生了1∶1主共振。由于有限元模型动力时程计算是从自重变形后的状态开始的，所以振动平衡位置不为零。拉索非线性振动有明显的“拍振”现象，即：发生共振时，具有“硬弹簧”性质的非线性振动幅值不会在外激励作用下持续增大，而是呈现周期性的涨落[2]。

为了对比各个节点的振动时程，观察振动的发展趋势。将各个节点的振动平衡位置设置为零，然后绘制各节点振动时程曲线的包络图(节点5振动为Y0方向，节点14,24,33为Y1方向)，如图10所示。

图10　各个节点振动时程曲线包络图 Fig.10 Envelopecurve of time history curve of the nodes

由图10可以看出，整体结构(节点5)在外激励的作用下发生了共振，振幅在前50 s内迅速增加，由于结构的振幅越来越大，拉索端点位移激励的幅值也越来越大，拉索⑤(1/2节点14)发生1∶1主共振幅值也越来越大。

整体结构的振幅没有在外激励作用下大幅增加，对于这个现象，本文认为，主要是由于索-梁相关振动导致拉索发生了1∶1主共振，外激励注入的能量较多地被转移到了拉索上，拉索的非线性振动“硬弹簧”效应限制了拉索的振幅，导致了“拍振”现象，也限制了整体结构的振幅。

观察图9与图10也可以发现，拉索中点沿Y1正方向振动的幅值要大于负方向的幅值。这体现了非线性振动的“振动漂移”现象。根据文献[2]中的理论描述与文献[14]的推导：在理论上，这是由于拉索非线性振动方程中恢复力项包含的2次项造成的，而这个2次项是由推导中记入了拉索垂度造成的。

取节点5的振动时程，作FFT变换，得到频谱图，如图11所示。

图11　节点5振动频谱图 Fig.11 Spectrogram curve of node 5

从图11中可以看出，当索-梁相关振动导致拉索主共振时，由于拉索大幅振动与整体结构振动的互相影响，导致整体结构中包含的主要频谱成分有所改变。

2.3频率比2∶1时结构索-梁相关振动特性

取重力加速度G=9.8 m/s2，设置图4中模型各个构件的参数如表2中所示。

表2　结构参数

按表2参数，考虑几何非线性，计算得到图4有限元模型在自重作用下的静力构型，拉索⑤,⑥,⑦的轴力分别为1.088E6 N, 1.486E6 N, 1.889E6 N，根据考虑垂度的拉索自振频率理论公式[11]，得到各拉索1阶自振频率分别为0.672 Hz,0.958 6 Hz, 1.870 Hz。计算图4有限元模型在自重静力构型下的动力特性，得到整体结构模态如图12所示。

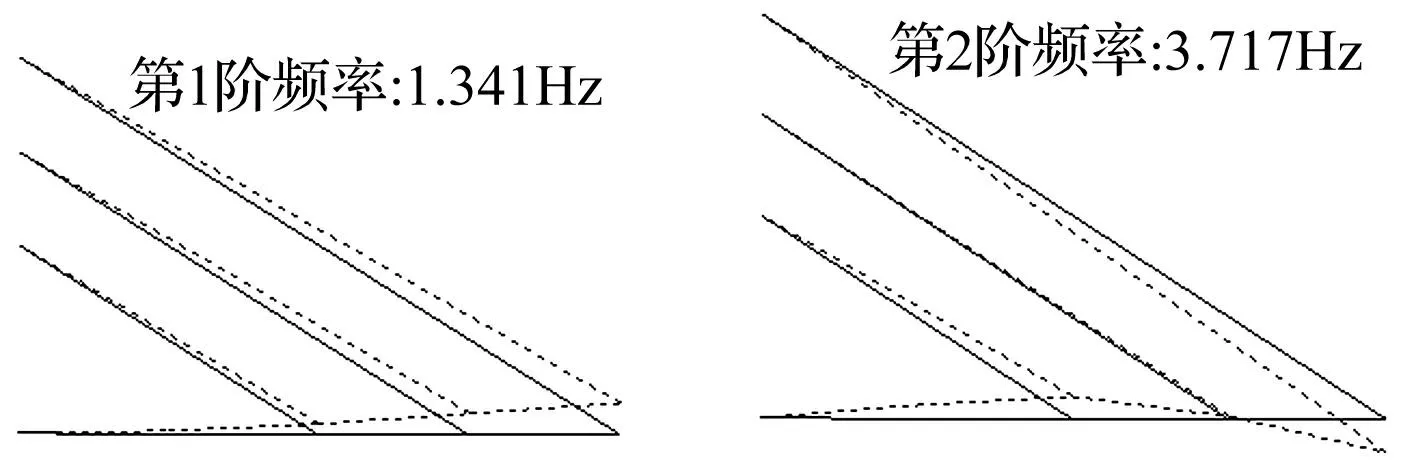
图12　结构振动模态 Fig.12 Vibration modes of the structure

可以看出，整体结构的1阶自振频率与拉索⑤的1阶自振频率比例关系接近2∶1。

按表2参数，建立图5有限元模型，考虑几何非线性计算结构在自重下静力构型，再计算结构动力特性如图13所示。

图13　结构振动模态 Fig.13 Vibration modes of the structure

由2.3节的频率响应曲线可以看出，当外激励作用下整体结构发生共振且整体结构自振频率与拉索自振频率呈一定比例关系时，拉索振幅较大。

所以，为了研究拉索在索-梁相关振动作用下发生参数共振的特性，使用图5有限元模型，在计算结构的静力构型后，在节点5上，沿Y0方向施加动态力P0sin(ωt)，设动态力频率为1.344 Hz,P0=-30 000 N。阻尼设置与2.2节相同，计算时间步长取为0.02 s，共计算10 000步。

将各个节点的振动平衡位置设置为零，然后绘制各节点振动时程曲线包络图(节点5为Y0方向，节点11,14,24,33为Y1方向)，以及主要关注的节点(节点11,14,5)的振动频谱图，如图14所示。

图14　各个节点振动时程曲线包络图、频谱图 Fig.14 Envelope curve of time history curve of the nodes and Spectrogram curve of the nodes

从图14(a)中可以看出，由于外激励频率接近整体结构的1阶自振频率，外激励造成了整体结构的共振，能量通过拉索端点传递到了拉索上。拉索⑤的1/2点(节点14)发生了大幅振动，同时拉索⑤的1/4点(节点11)也发生了大幅振动。拉索的非线性效应导致了节点发生振幅涨落的“拍振”，也限制了整体结构的振幅。

观察 14(b)可以看出，拉索⑤的1/2点的频谱曲线在拉索大幅振动时较为复杂，但主要的响应频率在0.69 Hz附近，接近拉索的1阶自振频率，这说明拉索发生了1阶参数共振。之所以响应频率稍大于拉索的1阶自振频率，这是由拉索非线性振动“硬弹簧”造成的振动硬化效应导致的[2]。

观察14(c)可以看出，拉索⑤的1/4点在拉索大幅振动时主要的响应频率在0.69 Hz,1.395 Hz这两个频率附近，且后者为前者数值的2倍。

这说明，由于拉索垂度较小，拉索的2阶自振频率接近1阶自振频率的2倍，外激励与拉索2阶自振频率接近1∶1的关系，外激励也导致拉索发生了2阶主共振。拉索1/4点的响应不仅包含了1阶参数共振，也包含了2阶主共振。

实际上，本节模型中发生索-梁相关振动时，1阶参数共振与2阶主共振在拉索⑤上是同时发生的耦合振动。对比图13中，有限元离散模型整体结构的第1阶模态与第4阶模态，也可以观察到这个趋势。

使用本文程序，通过提取计算结果，绘制了振动发展的动画，可以直观地观察到拉索上同时存在1阶参数共振与2阶主共振。但限于表达方式，以上结果只能用频谱图来说明。

从图14(d)中可以看出，由于本节模型发生索-梁相关振动时，拉索大幅振动的情况更为复杂，整体结构振动包含的主要频谱成分变得更加复杂。

2.4频率比不成倍时结构索-梁相关振动特性

在实际斜拉桥中，主梁的质量往往较大，拉索低阶自振频率很可能与整体结构自振频率是不匹配的，拉索低阶自振频率通常大于桥梁结构整体低阶自振频率。在本节内容中研究当索、梁频率不匹配时结构的索-梁相关振动特性。结构参数如表3所示。

表3　结构参数

按表3参数，考虑几何非线性计算，计算得到图4有限元模型在自重作用下的静力构型，拉索⑤,⑥,⑦的1阶自振频率分别为1.217 Hz, 1.724 Hz,2.861 Hz。计算图4有限元模型在自重静力构型下的动力特性，得到整体结构模态如图15所示。

图15　结构振动模态 Fig.15 Vibration modes of the structure

可以看出，整体结构的1阶自振频率与拉索⑤的1阶自振频率无1∶1与2∶1的比例关系。

按表3参数，建立如图5有限元离散模型，计算结构的自重静力构型下的模态为如图16所示。

图16　结构振动模态 Fig.16 Vibration modes of the structure

使用图5有限元模型，在计算结构的静力构型后，在节点5的Y0方向上施加动态力P0sin(ωt)，频率为0.8Hz,P0=-30 000 N 。阻尼设置与3.2节相同，步长取0.02 s，共计算10 000步。

将各个节点的振动平衡位置设置为零，然后绘制各节点振动时程曲线包络图(节点5为Y0方向，节点11,14,24,33为Y1方向)，如图17所示。

图17　各个节点振动时程曲线包络图 Fig.17 Envelopecurve of time history curve of the nodes

观察图17，可以看出，由于设定的外激励的频率与整体结构的1阶自振频率接近。整体结构在外激励作用下发生了共振，主梁上节点5的振幅增加较为迅速。在振动发展初期，拉索振动幅值增加较小。而在80秒左右，发生了拉索⑤(1/2节点14)的振动幅度迅速增加的共振现象。

为了研究这个现象，首先，截取0 s~80 s振动时程数据，对节点5的振动时程作FFT变换，得到振动频谱曲线，如图18所示。

图18　节点5与14振动频谱图 Fig.18 Spectrogram curves of node 5 and node 14

从图18的频谱曲线可以看出，在前80 s内，拉索⑤的1/2点振动频谱与主梁接近且振动幅值不大。这说明拉索只是在端点位移的带动下发生了振动，并未发生大幅共振。

截取80 s~100 s之间各个节点的振动时程曲线(节点5为Y0方向14,24,33为Y1方向)如图19所示。

图19　各个节点的振动时程曲线 Fig.19 Vibration envelopecurve of the nodes

如图19，可以看出，在85 s左右，拉索⑤的1/2点(节点14)发生了较大幅度的振动。这里截取共振现象最明显的85~95 s之间，节点14与节点5的振动时程，作FFT变换得到频谱曲线如图20所示。

图20　节点5与节点14振动频谱图 Fig.20 Spectrogram curve of node 5 and node 14

观察图20 ，可以发现，整体结构梁上节点5的频谱成分基本未发生变化，在0.8 Hz附近。拉索主要包含的频率成分为0.399 Hz,1.198 Hz。

本文判断，拉索⑤在80 s左右之所以发生大幅共振的原因是：由于整体结构振幅增加，拉索端点位移激励的幅值较大，且拉索自振频率大于端点位移激励的频率。索-梁相关振动激起拉索发生了 “超谐波共振”这一非线性振动的特有现象。

关于谐波共振发生的原因，文献[2,14]中通过建立拉索大幅振动的非线性方程，使用多尺度法从理论上做了较为详细的探讨。研究结果表明，对于非线性振动系统，振动方程的高次近似解中的谐波项与外激励的组合可能导致谐波共振(包括次谐波共振与超谐波共振)。数值计算与理论分析表明，系统阻尼对谐波共振的抑制作用更为明显，通常只有当外激励幅值较大时才可能发生较大幅值的谐波共振。

从图17与19中也可以看出，当外激励导致节点5的振幅达到接近1 m的时候(远大于图10与图14)，才激起拉索⑤发生共振。这时，外激励能量主要传递到拉索上，整体结构的振幅不再增大。

使用图5有限元模型，在计算结构的静力构型后，在节点5的Y0方向上施加动态力P0sin(ωt)，频率为1.22Hz,P0=-30 000 N 。阻尼设置与2.2节相同，时间步长取0.02 s，共计算10 000步。得到各个节点最大振幅的包络图如图21所示。

图21　各个节点振动时程曲线包络图 Fig.21 Vibration envelopecurve of the nodes

从图21中可以看出，由于设定的外激励频率与整体结构自振频率差别较大，整体结构不会在外激励作用下发生共振。外激励的频率接近拉索5的1阶自振频率，能量主要被拉索吸收，拉索5发生了1∶1主共振，由于整体结构的位移响应较小，拉索端部位移激励幅值不大，拉索主共振的响应相对较小，振动幅值的增加速度较慢。

3结论

(1)本文编制了非线性静/动力有限元计算程序，通过和ANSYS的对比，验证了程序的可靠性。从计算原理的本质来讲，非线性有限元动力时程积分算法能更好地体现结构大幅振动的受力细节。本文索-梁组合结构有限元模型动力时程计算结果中可以观察到“硬弹簧”、“拍振”、“振动漂移”、“谐波共振”等非线性振动的特有现象，有限元计算结果能与传统的非线性振动理论描述互相印证。

(2)对于索-梁组合结构，如果整体结构自振频率与拉索自振频率呈1∶1的关系，当主梁上外激励频率接近整体结构的自振频率时，索-梁相关振动容易导致拉索发生大幅主共振，外激励能量通过主梁传递到拉索上，导致整体结构的振幅不会大幅增加。由于拉索振动的非线性效应，拉索大幅振动的幅值也是有限的。拉索大幅振动与整体结构振动互相影响，导致整体结构的振动频谱特性变得复杂。

(3)如果整体结构自振频率与拉索自振频率呈2∶1的关系，当主梁上外激励频率接近整体结构的自振频率时，索-梁相关振动容易导致拉索发生大幅参数共振，外激励能量通过主梁传递到拉索上，整体结构振幅不会大幅增加。拉索振动的非线性效应导致拉索大幅振动的幅值也是有限的。由于结构中小垂度拉索的2阶自振频率接近1阶自振频率的2倍，拉索会在端点位移激励下发生1阶参数共振，同时发生2阶主共振，这两种大幅振动模态是耦合的，这种情况下，拉索索力变化更加复杂，导致整体结构的振动频谱特性更加复杂。

(4)如果整体结构频率与拉索频率不成倍匹配。当主梁上外激励接近整体结构的自振频率时，振动发展初期，索-梁相关振动不容易导致拉索发生大幅振动，振动的能量传递不明显，拉索振动的非线性效应不明显，整体结构容易发生大幅振动。当激励持续时间较长，整体结构振动幅值较大导致拉索端部位移激励较大时，索-梁相关振动有可能导致拉索发生“谐波共振”，这时，拉索振动非线性效应变得明显，整体结构与拉索之间发生能量传递，限制了整体结构振幅的增加。

(5)对于索-梁组合结构，若梁上外激励频率与整体结构频率不匹配，但外激励频率接近某根拉索自振频率时，拉索在外激励作用下容易发生共振，外激励能量较多地被发生共振的拉索吸收。由于外激励不会造成整体结构共振，整体结构吸收能量较少，端点位移激励的幅值较小，这种情况下拉索发生的共振幅值相对较小，振幅增加速度也较慢。

参考文献

[1]Max Irine H, Cable Structure[M]. The MIT Press, 1981.

[2]Nayfeh A H, Mook D T. Nonlinear oscillations[M]. Wiley, New York,1984.

[3]汪至刚, 孙炳楠. 斜拉桥参数振动引起的拉索大幅振动[J].工程力学, 2001,18(1): 103-109.

WANG Zhi-gang, SUN Bing-nan. Cable vibration for cable stayed bridge by parametric response[J]. Engineering Mechanics, 2001,18(1): 103-109.

[4]Lilien J L. Pinto da Costa A. Vibration amplitudes caused by parametric excitations of cable stayed structurs[J].Sound Vibrat, 1994,174(1):69-90.

[5]陈水生.大跨度斜拉桥拉索的振动及被动、半主动控制[D]. 杭州：浙江大学,2002.

[6]于岩磊,高维成,孙毅. 斜拉索参数振动精细化模型及其影响因素研究[J]. 工程力学,2010(s2):178-185.

YU Yan-lei, GAO Wei-cheng, SUN Yi. Study on refined model and influence factoes of parameiric vibration of inclined cables[J]. Engineering Mechanics,2010(s2): 178-185.

[7]De Sá Caetano E. Cable Vibrations in Cable-Stayed Bridges [M]. IABSE,2007.

[8]Gattullia V, Lepidib M, John H G, et al. One-to-two global-local interaction in a cable-stayed beamobserved through analytical, finite element and experimental models[J]. International Journal of Non-Linear Mechanics, 2005,40(21):571-588.

[9]ZHANG He, XIE Xu. Dynamic responses of cable-stayed bridges to vehicular loading including the effects of the local vibration of cables[J]. Journal of Zhejiang University-Science A: Applied Physics & Engineering,2011,12(8): 593-604.

[10]陈丕华,王修勇, 陈政清,等.斜拉索面内参数振动的理论和试验研究[J].振动与冲击,2010,11(2):50-53.

CHEN Pi-hua, WANG Xiu-yong, CHEN Zheng-qing ,et al. Theoretical and experimental study on planar parametric oscillations in a stayed-cable[J]. Journal of Vibration and Shock, 2010,11(2):50-53.

[11]王涛, 沈锐利. 斜拉桥索-梁相关振动概念与研究方法初探[J]. 振动与冲击, 2013,20(32):29-34.

WANG Tao, SHEN Rui-li. Primary investigation on the concept and method of cable-beam vibration in cable-stayed bridge[J]. Journal of Vibration and Shock,2013,20(32):29-34.

[12]唐茂林. 大跨度悬索桥空间几何非线性分析与软件开发[D].成都:西南交通大学, 2003.

[13]潘永仁. 悬索桥结构非线性分析理论与方法[M].北京：人民交通出版社,2001.

[14]王涛. 斜拉桥拉索参数振动的理论与数值分析[D].成都：西南交通大学,2009.