基于快速多极子基本解方法(FMM-MFS)的弹性波二维散射模拟研究
2016-01-12刘中宪,王冬,梁建文
第一作者刘中宪男,副教授,博士后,硕士生导师,1982年生
基于快速多极子基本解方法(FMM-MFS)的弹性波二维散射模拟研究
刘中宪1,2,王冬1,2,梁建文3
(1 天津城建大学土木工程学院,天津300384; 2 天津市软土特性与工程环境重点实验室,天津300384;3.天津大学土木工程系,天津300384)
摘要:针对弹性波二维散射问题,发展一种新的快速多极子基本解方法(FMM-MFS)。方法基于单层位势理论,通过在虚边界上设置膨胀波线源和剪切波线源以构造散射波场,从而避免了奇异性的处理和边界单元离散;结合快速多极子展开技术(FMM),大幅度降低了计算量和存储量,突破了传统方法难以处理大规模散射问题的瓶颈。以全空间孔洞对P、SV波的二维散射为例,给出了具体求解步骤,并在个人计算机上实现了上百万自由度问题的快速精确计算。在方法效率和精度检验基础上,分别以单孔洞和随机孔洞群对平面波(P、SV波)的散射为例进行计算模拟,揭示了孔洞(群)周围弹性波散射的若干重要规律。
关键词:基本解方法;快速多极子展开方法;快速多极子基本解方法(FMM-MFS);弹性波散射
基金项目:国家自然科学
收稿日期:2013-12-30修改稿收到日期:2014-03-12
中图分类号:Tp12;Tp13.3文献标志码:A
FMM-MFS soluton to two-dimensinal scattering of elastic waves
LIUZhong-xian1,2,WANGDong1,2,LIANGJian-wen3(1. College of Civil Engineering, Tianjin Chengjian University, Tianjin 300384, China;2. Tianjin Municipal Key Laboratory of Soft Soils and Engineering Environment, Tianjin 300384, China; 3. Department of Civil Engineering, Tianjin University, Tianjin 300072, China)
Abstract:A new algorithm named the fast multipole fundamental solution method(FMM-MFS) was presented for calculating two-dimensional elastic wave scattering problems. The algorithm could avoid the singularity of matrix by placing the line sources of compressional wave and shear wave on a virtual boundary based on the single layer potential theory, and avoid elements discretization on the boundary. Combined with FMM, MFS can solve large-scale problems of wave scattering with greatly reducing computation and the memory requirement. Taking the two-dimensional scattering of P and SV waves around a cavity in elastic full-space as an example, the implement procedures were presented in detail, and up to millions of DOF’s scattering problems were solved successfully on a personal computer. Based on the tests of accuracy and efficiency of FMM-MFS, the scatterings of plane waves around a cavity and randomly distributed group cavities in full-space were solved. Several important conclusions about scattering of elastic waves around cavity(cavities) were obtained.
Key words:method of fundamental solutions (MFS); fast multipole expansion method (FMM); FMM-MFS; scattering of elastic wave
弹性波散射是机械、材料、地球物理、地震学等多个领域的一个研究热点。在众多弹性波动模拟方法中,基本解方法(MFS),除了具有边界元方法降维求解、自动满足无限远辐射条件的优势,同时具有无奇异性、无网格特性以及极高的数值精度,近些年来在声波、电磁波以及弹性波波场模拟中获得了广泛应用[1-2]。该方法最初源于Kupradze等[3-4]的工作,其基本思路是在边界附近假想一虚拟边界,并在其上布置虚拟波源来构造域内散射波场,其本质在于利用一系列格林函数解的线性组合给出偏微分方程的近似解,各基本解未知系数需首先根据边界条件求出。因此MFS也可看做是一种特殊的间接边界积分方程法,并和Treffez方法具有很大的相似性[5],非常适合无限域中波动问题求解。
然而在实际工程应用中,MFS的一个显著弱点在于其求解方程矩阵的稠密特性严重影响了高自由度问题(如大尺度、高频或多体散射)求解的计算效率。针对该问题,近些年来一些学者尝试将快速多极子展开(FMM)技术运用到了MFS求解当中。FMM通过将核函数表达式场点和源点分离,将原来的源点、场点间单粒相互作用转换为粒组与粒组之间的作用,从而大幅度降低存储量,并显著提高计算效率[6-8]。最新发展的FMM能够将MFS的计算量和存储量均降低到O(N)量级,使大规模工程问题快速求解成为可能[9-11]。需注意的是,上述文献分别针对位势问题、静力分析和声场模拟,对于固体中弹性波散射问题FMM-MFS求解,据作者所知,目前国内外相应的研究较少。而需指出的是,相关的快速多极边界元方法求解在国内外已有一些报道[12-13]。
即针对无限域或半无限域中大规模弹性波动问题求解(二维平面问题),基于单层位势理论,发展一种新的快速多极子基本解方法。在格林函数矩阵建立和虚拟波源强度求解中,引入快速多极子展开。该方法整体求解思路比较直观,且便于数值实现。以全空间孔洞周围P、SV波散射为例给出了具体求解步骤,进而通过典型算例验证了方法的计算精度和求解效率。最后以全空间单孔洞对P、SV波的高频散射和随机分布孔洞群对P、SV波的散射为例,验证方法对实际复杂问题的适应性并得出了一些重要结论。
1弹性波散射常规基本解方法(MFS)
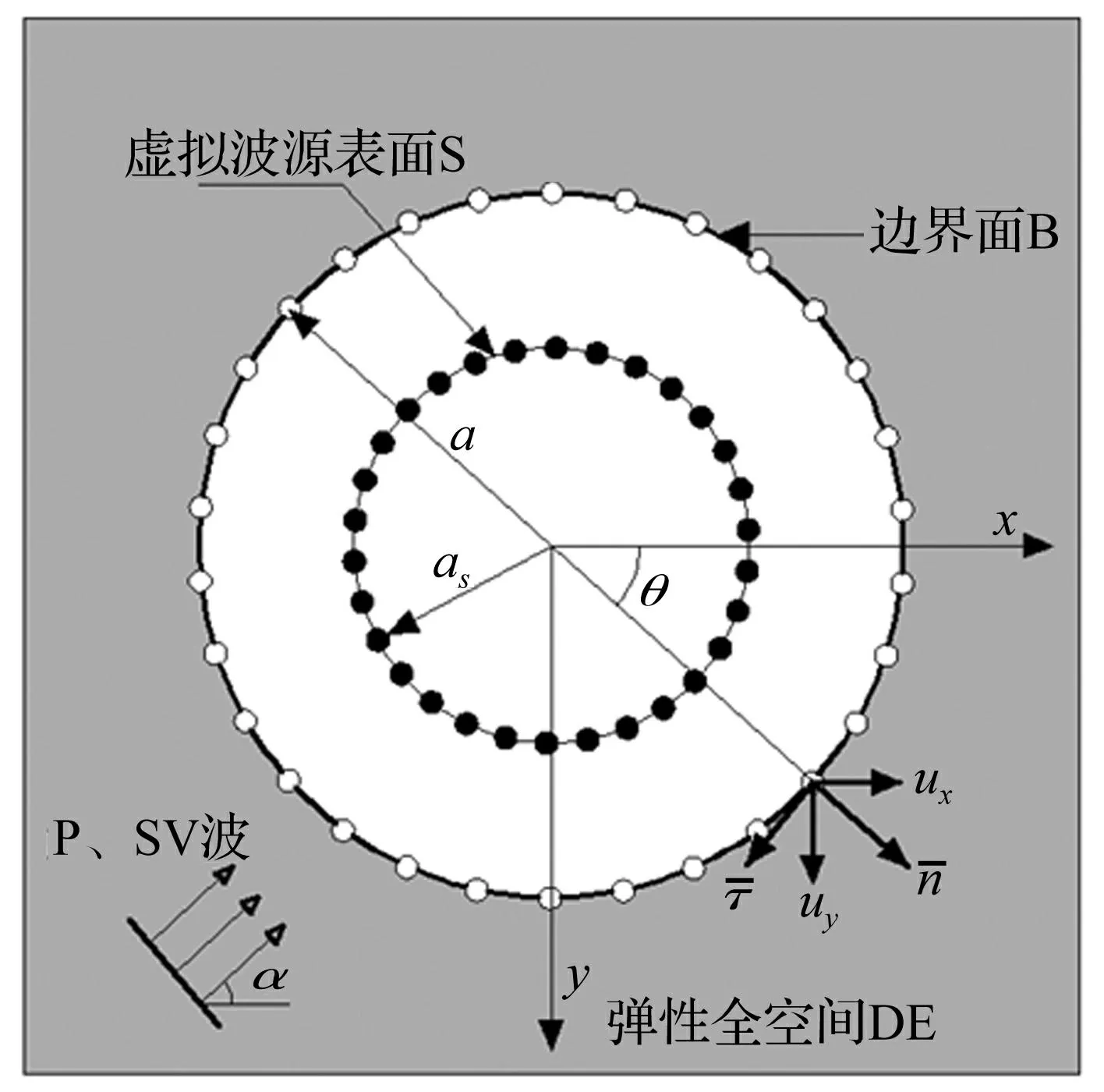
图1 计算模型 Fig.1 Calculation model
为便于说明,首先以全空间圆形孔洞周围P、SV波散射为例,阐述常规基本解方法(MFS)的具体实现步骤。计算模型如图1所示,无限域中一足够长圆柱形孔洞,假设平面P或SV波从左侧水平入射(α=0°),波面平行于孔洞纵轴,待求问题为平面应变状态下的弹性波散射。基于单层位势原理,可在孔洞内部一虚拟源面S上施加虚拟波源以构建散射波场。根据孔洞边界零应力条件构建方程以求解波源强度,进而计算散射场位移,将其和自由场位移叠加即得到总场位移。根据试算经验,图中虚拟波源面S的最优半径低频时取0.4~0.6倍散射体半径,高频时则扩大至0.7~0.9倍。该方法对于半无限空间弹性波散射问题也是同样适用的,仅需在受散射波影响的半空间地表附近布置虚拟波源即可。
1.1散射场构造
根据叠加原理,总位移场和应力场可分别表达为:
u(x)=uf(x)+us(x)
(1a)
σ(x)=σf(x)+σs(x)
(1b)
式中:uf、σf分别表示平面波入射下自由场位移和应力(无孔洞时),us、σs表示散射场位移和应力。
由Helmholtz矢量分解原理,二维平面应变下位移场可表达:
u=φ+×(0,0,ψ)
(2)
式中:φ和ψ分别为P波、SV波势函数, 满足下列运动方程:
(Δ+h2)φ=0
(3a)
(Δ+k2)ψ=0
(3b)
式中,Δ为二维拉普拉斯算子,h和k分别为P波和SV波波数。由各向同性假设,应力可表达为:
σij=λuk,kδi,j+μ(ui,j+uj,i)
(4)
根据单层位势理论,散射场可由面S上分布的虚拟波源产生,相应位移和应力可表达为:
x∈DE,x1∈S
(5a)
x∈DE, x1∈S
(5b)

(6a)
(6b)
由式(2)和式(4),全空间中膨胀波、剪切波动力格林函数可表达如下:
膨胀波线源:
(7a)
(7b)
γ=k/h
(7c)
γ=k/h
(7d)
(7e)
剪切波线源:
(8a)
(8b)
(8c)
(8d)
(8e)
1.2边界条件及求解
根据孔洞边界上零应力条件:

(9a)

(9b)
圆形孔洞情况,边界法线方向余弦为(cosθ,sinθ),正向和切向应力可表达如下:
σnn=σxxcos2θ+σyysin2θ+2σxysinθcosθ
(10a)
σnt=(-σxx+σyy)sinθcosθ+σxy(cos2θ-sin2θ)
(10b)
根据孔洞表面自由边界条件,式(9a)、(9b)可表示为:
(11a)
xn∈B,xm∈S;n=1,…,N
(11b)
式中:cm、dm代表第m个膨胀波和剪切波线源强度,T代表应力。通过式(11)计算波源强度,代入式(5a)、(5b)即可求出无限域中任意一点的位移和应力。
在上述求解中,采用常规高斯消元法求解时,系数矩阵{Tij}为满阵,解大规模问题时其效率低下且存储量大。下面考虑结合广义极小余量法(GMRES)[14]和快速多极子展开技术,突破常规MFS求解大规模问题的计算瓶颈。
2弹性波散射FMM-MFS方法
FMM-MFS使用树结构作为主要的存储和运算对象,结合GMRES迭代算法,通过核函数的多极展开、多极展开传递(M2M)、多极展开向局部展开传递(M2L)、局部展开传递(L2L)以及局部展开5个步骤,避免了对系数矩阵的直接存储和对线性方程组的直接求逆。与传统MFS相比,对于高自由度问题,FMM-MFS大幅度提高了计算效率和经济性,可将存储量和计算量降至O(N)量级。下面,首先阐述FMM-MFS的基本原理,进而给出弹性波散射FMM-MFS解答过程。
2.1FMM-MFS基本原理
2.1.1模型边界离散与树结构生成

图2 自适应树结构 Fig.2 The adaptive tree structure
首先对计算模型边界进行数值离散(配点)和树结构生成。对于二维问题,这里使用四叉树结构。将图1中弹性体边界离散为N个边界点,同时构建虚拟荷载面S,同样离散为N个点,称之为源点。获取各离散边界点和源点的平面坐标。注意整个过程并不需要引入单元网格。这与常规边界元法一致。然后,将二维弹性体全部边界放置于一足够大的正方形中,此正方形代表树结构的根结点,称作0层;将大正方形分成4个小正方形,称作第1层;依次类推,将正方形所包含的边界点数达到预设值为止,删除不包含任何边界点的正方形。每个正方形代表一个树结点,叶子结点则不再包含任何子正方形。
图2中展示了图1计算模型的四叉树结构划分(a)及其示意图。其中方形四叉树示意图(b)为边界点树结构,圆形四叉树示意图(c)为虚拟源点树结构。图2中,源点树结构主要存储多极展开系数、多极展开传递系数;边界点树结构主要存储局部展开传递、局部展开系数;多极展开向局部展开传递则由两部分共同存储。
2.1.2核函数的多极展开
下面对式(11)中形如Tij(xn,xm)的核函数进行展开。从源点开始,将源点信息传递到对应的叶子结点中心,这一过程称为多极展开。
参考文献[15]中展开方式,假设计算式(11)中核函数为K(x,y)。在进行展开之前需要指出:本文中多极展开在源点Y处进行,而局部展开则在边界点X处进行。
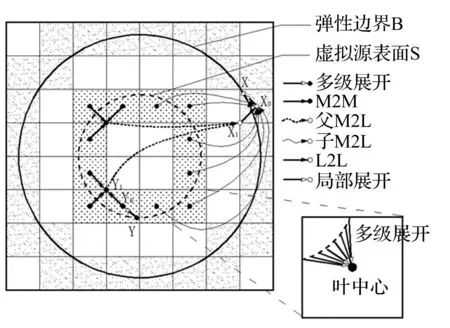
图3 快速多极展开相关点 Fig.3 The related points for FMM

K(x,y)=N(x,y0)M(y0,y)
(12)
式中:M(y0,y)称为展开点y0(源点叶子结点)的多极展开系数。这里,M(y0,y)只与y0变化有关,故只需计算一遍即可和满足条件的任意点x进行计算。
2.1.3多极展开的传递(M2M)
如图3,当展开点从y0移到较近点y1(源点父结点)时,可得到新的展开系数,即:
M(y1,y)=I(y1,y0)M(y0,y)
(13)
由式(11)可以看出,我们不需要重新计算展开系数,仅需将已计算的多极展开系数平移即可得到新的展开系数。其中,I(y1,y0)为多极展开传递系数。
2.1.4多极展开向局部展开的传递(M2L)

N(x,y0)=L(x,x0)H(x0,y0)
(14)
式中:L(x,x0)即为局部展开系数。与此同时,式(14)同样满足多极展开向局部展开的传递关系(M2L),其中H(x0,y0)即为传递系数。
在进行局部展开之前,需要了解“邻居”和“相互作用列表”两个概念。结点M的“邻居”是指与M位于同一层且至少有一个角点共用,一个结点至多有8个“邻居”。结点M的“相互作用列表”是指某结点的父结点与M的父结点互为“邻居”且本身与结点M不为“邻居”,一个结点至多有27个“相互作用列表”,如图4所示。

图4 结点“邻居”与“相互作用列表” Fig.4 Adjacent cells and cells in the interaction list
2.1.5局部展开的传递(L2L)
如图4,当局部展开点从x0移到较近点x1(边界父结点)时,可得到新的局部展开系数,即:
L(x,x1)=L(x,x0)J(x0,x1)
(15)
由式(15)可以看出,新的局部展开系数不需要重新计算,仅需将已计算的局部展开系数平移即可得到新的局部展开系数。其中,J(x0,x1)即为局部展开传递系数。
2.1.6FMM-MFS的实施
依据快速多极子基本解方法的基本原理,将其具体实施过程表述如下:
(1)将弹性体边界离散化,这与常规MFS方法一致,进而自动生成自适应树结构。
(2)从源点y开始,将源点信息传给叶子结点,通过式(12)在叶子中心展开形成多极展开系数。
(3)根据需要,可将多级展开点平移至对应父结点(M2M),计算式(13)构成传递关系。在这一步中可多次向上层父细胞传递,在满足精度的条件下尽可能多的往上传递。
(4)将源点树结构各层结点的多极展开系数传递给边界点树结构同层相应结点,形成局部展开系数(M2L),式(14)构建此关系。所谓“相应”,即边界父结点接收非“邻居”的多极展开系数,边界子结点(非最底层父结点)接收“相互作用列表”的多极展开系数。
(5)式(15)将边界点树结构中各层结点的局部展开系 数层层传递直到叶子结点(L2L)。至此,将叶子结点处累加而来的所有局部展开系数通过局部展开传给边界点x,完成整个展开以及传递过程。剩余近场源点,即叶子结点的邻居以及自身所包含的源点,直接采用常规MFS计算。
经过上述5个步骤,核函数K(x,y)最终展开为:
K(x,y)=
L(x,x0)J(x0,x1)H(x1,y1)I(y1,y0)M(y0,y)
(16)
式中:H(x1,y1)为M2L系数,其余函数均已说明。
计算过程中,采用GMRES进行迭代求解运算。为降低迭代次数,在GMRES求解前采用预处理技术[16],这里可采用近场格林函数解构造窄带稀疏矩阵,对方程组进行预处理。
2.2弹性波二维散射FMM-MFS解答
根据式(6a)和(6b)全空间势函数形式,采用Graf加法定理[17]:
(17)
式中:Z可以是J、Y、H(1)、H(2)以及他们的线性组合,n为截断数,其中几何参数如图5所示。

图5 符号定义 Fig.5 Symbol definition
(18)

(20)
Jm(kρ′)eimγ′=
(21)

(22)
将上式分别代入式(7)即可求出位移和应力。同理,可导出式(6a)展开式,仅需将式(22)中的剪切波波数k改为纵波波数h即可,此处不再赘述。
上述即为全空间中弹性波平面内二维散射的快速多极基本解方法解答。对于半空间情况,可利用相应的半空间格林函数进行展开求解,或者仍采用全空间基本解,但需对受散射波影响的半空间表面进行离散。
3数值算例与分析
3.1FMM-MFS计算精度及效率检验
首先以全空间孔洞为例,检验快速多极基本解方法的精度、迭代收敛速度及数值稳定性。这里引入无量纲频率η的概念。它定义为散射体等效直径与入射波波长之比,即:η=2a/λ=ωa/πβ。分别利用快速多极子基本解方法和解析解即波函数展开法计算全空间圆形孔洞对平面P、SV波的散射。其孔洞直径取10 m,入射波频率取为100 Hz,介质剪切波速取1 000 m/s,泊松比取为0.25,换算无量纲频率η=1,图6为全空间孔洞表面位移幅值结果对比情况。边界配点数取N=1 000,即自由度数为2 000。容易看出,本文所发展快速多极子基本解方法同解析解结果吻合良好。
图7为传统基本解方法与快速多极子基本解方法的迭代收敛残差与迭代步关系曲线,展开截断阶数取为20。从图中可以看出,两种方法迭代收敛速度相当; FMM-MFS方法下,自由度数不同其收敛速度也相当,从而证明了此方法的良好收敛性。图8给出了P波入

图6 全空间孔洞表面位移幅值FMM-MFS和解析解 Fig.6 Comparisons between the displacement amplitude around the cavity by FMM-MFS and that of analytic solution

图7 迭代收敛曲线 Fig.7 The convergence of the iteration curve

图8 FMM-MFS与常规MFS 的总CPU时间结果比较 Fig.8 Comparisons between the total CPU time of FMM-MFS and that of MFS
射时计算时间随自由度之间的关系,入射波频率取η=5.0,入射角度取α=0,即水平入射。其中父细胞划分到7层,级数累加从-6到6;叶子细胞划分到11层,级数累加从-1到1。从图中可清晰看出,自由度超过5 000以后,常规算法计算时间急剧增加。10 000自由度时计算时间已经达到约25 000 s,远远大于FMM-MFS计算160万自由度计算时间。而且,常规方法的内存需要量大,目前一般个人台式电脑也只能算至大约两万自由度。然而,采用FMM-MFS方法,160万自由度问题仅需约9 000 s,证明了FMM-MFS的计算效率远远高于传统MFS,且突破了传统MFS不能计算大规模问题的弱点。
为检验本文方法数值稳定性,表1给出了不同边界配点数下FMM-MFS位移幅值计算结果,配点数分别取2 000、20 000和100 000。由表可知,随配点数增大,孔洞表面位移幅值相差仅在小数点后7位,位移结果收敛良好,反映了该方法具有良好的数值稳定性。
以上的计算结果以及计算时间统计,均是在8G内存、32位XP操作系统的个人电脑上(Dell Pretision T5500),使用Matlab进行编程运算得到。
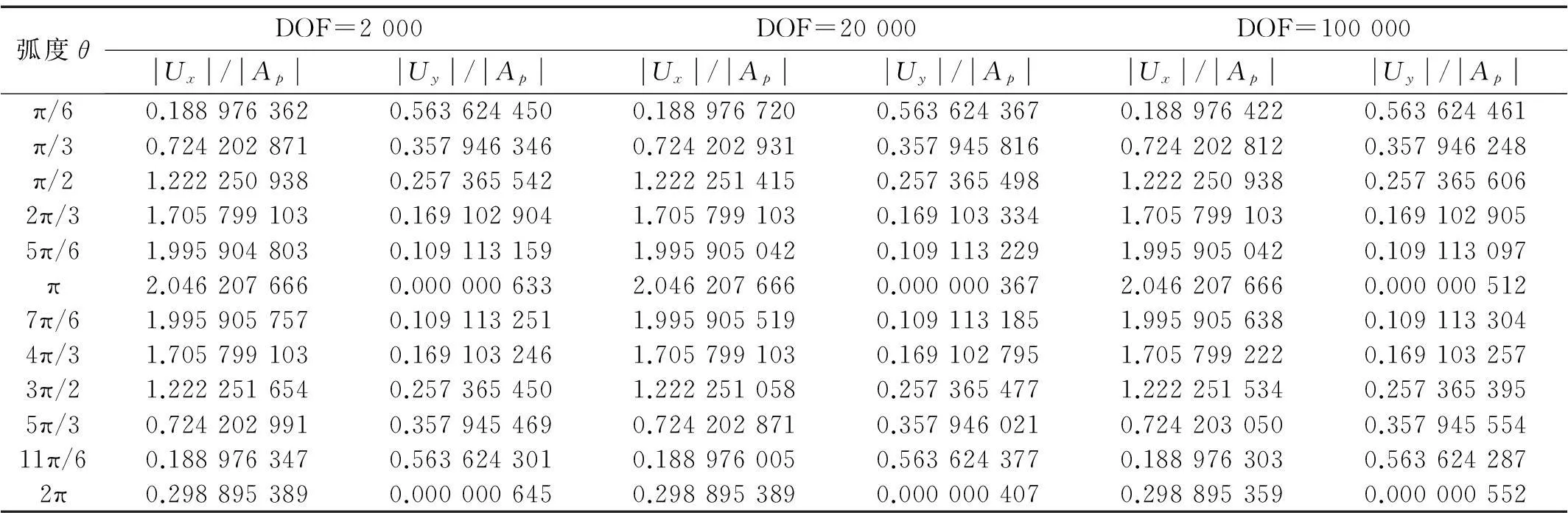
表1 位移幅值数值稳定性检验 (η=1.0)
3.2全空间单孔洞对平面P、SV波的高频散射
图9给出了高频P、SV波入射下,全空间单孔洞面上的位移结果。图10分别给出了高频P、SV波入射下,全空间孔洞附近15倍孔洞半径范围内的x、y方向位移幅值云图。孔洞直径取100 m,入射波频率取为500 Hz,介质剪切波速取1 000 m/s,泊松比取为0.25,换算为无量纲频率η=50。入射角度取0°,即左侧水平入射。
为充分提高计算精度和计算效率,孔洞表面离散5 000点(自由度10 000)。分别采用常规MFS和FMM-MFS计算,计算机耗时分别约为6 000 s和410 s,FMM-MFS计算时间不同于η=5.0是因为划分层数不同所导致。结果表明本文方法能够高效精确地求解高频波散射问题。另外容易看出,高频P、SV波水平入射,迎波面一侧出现显著的位移放大效应(集中在一倍孔洞半径范围内),位移幅值达到入射波幅值的2倍多,在孔洞右侧则呈现很长的“阴影区”,表明孔洞对高频P、SV波有很强的“屏障”效应。因此,地下结构抗爆设计尤需注意迎爆面的动应力集中效应。

图9 P、SV波入射下孔洞表面位移幅值 (η=50) Fig.9 Displacement amplitude on the cavity surface for P 、SV waves incident(η=50)

图10 P、SV波入射下孔洞附近位移幅值云图 Fig.10 Displacement amplitude in the neighborhood of the cavity for P 、SV waves incident
3.3全空间孔洞群对平面P、SV波的散射
为考察FMM-MFS方法对复杂的多体散射问题求解的适应性,图11、12分别给出随机分布的孔洞群对P、SV波的散射结果。选取与图10所示相同范围内随机分布的30个圆形孔洞为计算模型,水平左侧入射,孔洞直径取为100 m,入射频率分别取1、5、10、20 Hz,介质剪切波速1 000 m/s,泊松比0.25,换算无量纲频率η=0.1、0.5、1.0、2.0。分别给出了不同频率P、SV波水平入射下孔洞附近x、y方向位移幅值云图。

图11 P波入射下随机多孔洞周围位移云图 Fig.11 Displacement amplitude in the neighborhood of random group cavities for P waves incident
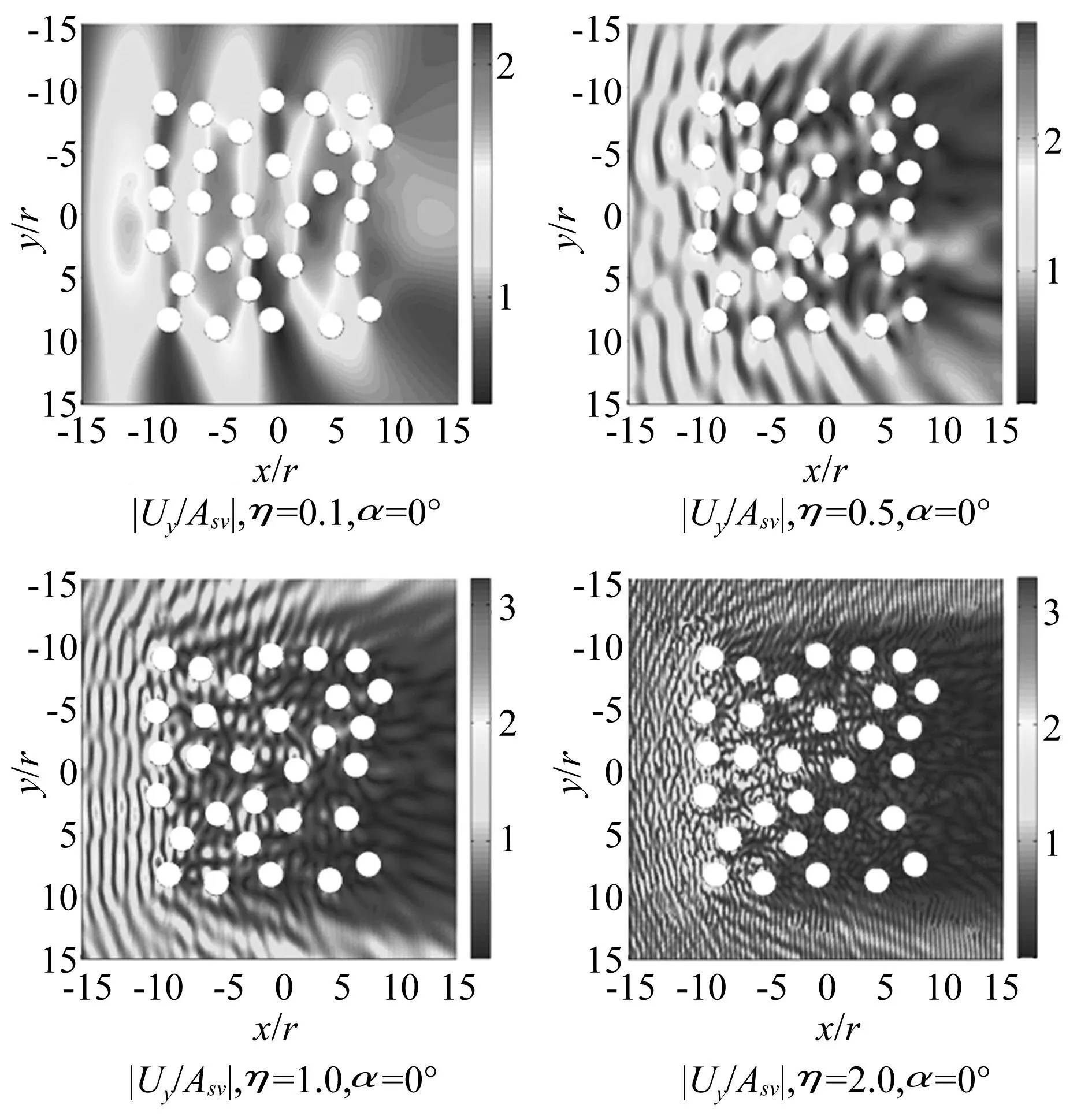
图12 SV波入射下随机孔洞群周围位移云图 Fig.12 Displacement amplitude in the neighborhood of random group cavities for SV waves incident
结果表明:P、SV波左侧水平入射下,受孔洞群之间散射波相互干涉影响,孔洞群对P、SV波的散射与单孔洞情况具有明显差别,孔边动力放大效应更为显著,即便是在低频η=0.1情况,位移放大系数接近2倍(单洞时则表现为弱散射)。而在孔洞群的右侧,位移幅值很小,可以看出孔洞群对入射P、SV波的“屏障”效应更为明显。随着入射波频率增加,孔洞间散射波的相干效应更为强烈。如η=2.0时,迎波面一侧前两列孔洞边缘出现显著的位移放大效应,P、SV波入射下放大系数峰值分别达到4.5和3.2。值得指出的是,对于η=2.0情况,模型计算自由度约为6 000,计算时间仅为100 s,即实现了孔洞群对波散射高效精确求解。
4结论
针对弹性波二维散射问题,基于单层位势理论,结合快速多极子展开技术,发展了一种新的快速多极子基本解方法。数值分析表明:该方法具有高精度、良好的收敛性及数值稳定性、无网格特性,在提高运算速度的同时能够大幅度降低计算存储量。通过算法优化,可在目前主流计算机上实现数百万自由度弹性波散射问题的快速精确求解。最后以全空间单孔洞和随机分布孔洞群对P、SV波散射为例,研究了孔洞周围高频波散射和多体散射的若干规律,可为孔隙介质波动分析、材料无损检测等提供部分理论依据。另外,本文方法对于大规模声波、电磁波散射分析等同样具有参考价值。
参考文献
[1]Golberg M A, Chen C S. The method of fundamental solutions for potential, Helmholtz and diffusion problems[J]. Boundary Integral Methods-Numerical and Mathematical Aspects, 1998: 103-176.
[2]Fairweather G, Karageorghis A, Martin P A. The method of fundamental solutions for scattering and radiation problems[J]. Engineering Analysis with Boundary Elements, 2003, 27(7): 759-769.
[3]Kupradze V D, Aleksidze M A. The method of functional equations for the approximate solution of certain boundary value problems[J].USSR Computational Mathematics and Mathematical Physics, 1964, 4(4): 82-126.
[4]Mathon R,Johnston R L. The approximate solution of elliptic boundary-value problems by fundamental solutions[J]. SIAM Journal on Numerical Analysis, 1977, 14(4): 638-650.
[5]Chen J T, Lee Y T, Yu S R, et al. Equivalence between the Trefftz method and the method of fundamental solution for the annular Green’s function using the addition theorem and image concept[J]. Engineering Analysis with Boundary Elements, 2009, 33(5): 678-688.
[6]Greengard L, Rokhlin V. A fast algorithm for particle simulations[J]. Journal of Computational Physics, 1997, 135(2): 280-292.
[7]姚振汉,王海涛. 边界元法[M].北京:高等教育出版社,2009.
[8]崔晓兵, 季振林. 快速多极子边界元法在吸声材料声场计算中的应用[J]. 振动与冲击, 2011, 30(8): 187-192.
CUI Xiao-bing, JI Zhen-lin. Application of FMBEM to calculation of sound fields in sound-absorbing materials[J].Journal of Vibration Engineering. 2011, 30(8): 187-192.
[9]Liu Y J, Nishimura N,Yao Z H. A fast multipole accelerated method of fundamental solutions for potential problems[J]. Engineering Analysis with Boundary Elements, 2005, 29(11): 1016-1024.
[10]许强, 蒋彦涛, 张志佳. 快速多极虚边界元法对含圆孔薄板有效弹性模量的模拟分析[J]. 计算力学学报, 2010, 27(3): 548-555.
XU Qiang,JIANG Yan-tao,ZHANG Zhi-jia. Fast multipole VBEM for analyzing the effective elastic moduli of a sheet containing circular holes[J].Chinese Journal of Computational Mechanics, 2010, 27(3): 548-555.
[11]Jiang X R, Chen W, Chen C S.A fast method of fundamental solutions for solving Helmholtz-type equations[J]. International Journal of Computational Methods, 2013,10(2),1341008.
[12]Chen Y H, Chew W C, Zeroug S. Fast multipole method as an efficient solver for 2D elastic wave surface integral equations[J]. Computational Mechanics, 1997, 20(6): 495-506.
[13]Chaillat S, Bonnet M, Semblat J F. A new fast multi-domain BEM to model seismic wave propagation and amplification in 3-D geological structures[J]. Geophysical Journal International, 2009, 177(2): 509-531.
[14]Saad Y, Schultz M H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869.
[15]Yoshida K. Applications of fast multipole method to boundary integral equation method[D]. Dept. of Global EnvironmentEng., Kyoto Univ., Japan, 2001.
[16]王海涛. 快速多极边界元法在二维弹性力学中的应用[D]. 北京:清华大学, 2002.
[17]Utsunomiya T, Watanabe E, Nishimura N. Fast multipole algorithm for wave diffraction/ radiation problems and its application to VLFS in variable water depth and topography[C]//Proc 20th Int Conf on Offshore Mech and Arcctic Engrg,2001.

