地震作用下斜交简支梁桥桥面旋转反应的参数分析
2016-01-12沈贤,王军文,李建中等
第一作者沈贤男,硕士生,1986年生
通信作者王军文男,博士,教授,1971年生
邮箱:wjunwen2901@163.com
地震作用下斜交简支梁桥桥面旋转反应的参数分析
沈贤1,2,王军文1,2,李建中3,胡玉娟1,吴天宇1,2
(1.石家庄铁道大学土木工程学院,石家庄050043;2. 石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室,石家庄050043;3. 同济大学桥梁工程系,上海200092)
摘要:地震引起的斜交简支梁桥桥面面内旋转不仅增大了梁体的纵、横向位移,而且增加了梁体与边界碰撞的几率。为研究地震作用下斜交简支梁桥桥面的旋转反应,利用OpenSees地震仿真模拟平台,建立考虑梁体与桥台间纵向碰撞、梁体与挡块间横向碰撞效应的斜交简支梁桥简化动力计算模型,分析梁体与桥台间纵向碰撞刚度、伸缩缝间隙、梁体与挡块间碰撞刚度、初始间隙、挡块力学特性等对斜交简支梁桥桥面旋转的影响。结果表明:纵向碰撞刚度、伸缩缝间隙、梁体与挡块间初始间隙对斜交简支梁桥桥面转角的影响较大,而横向碰撞刚度对桥面转角的影响相对较小;梁两端锐角区设置纵向垫块对减小桥面转角和纵向位移有较好的效果;设置弹塑性挡块能有效控制桥面的震致转动,减轻挡块的横向受力。
关键词:地震;斜交简支梁桥;桥面旋转;碰撞效应;地震响应
基金项目:国家自然科学
收稿日期:2014-02-24修改稿收到日期:2014-04-03
中图分类号:U448.41文献标志码:A
Parametric analysis for deck’s inplane rotation responses of simply-supported skewed girder bridges under ground motions
SHENXian1,2,WANGJun-wen1,2,LIJian-zhong3,HUYu-juan1,WUTian-yu1,2(1. School of Civil Engineering, Shijiazhuang TieDao University, Shijiazhuang 050043, China; 2. Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education,Shijiazhuang TieDao University, Shijiazhuang 050043, China; 3. Department of Bridge Engineering, Tongji University, Shanghai 200092, China)
Abstract:The deck’s inplane rotation caused by seismic responses of simply-supported skewed girder bridges(SSGB) not only increases the longitudinal and transverse displacements of deck but also increases the probability of pounding between girder and boundary. In order to investigate the deck’s seismic inplane rotation response of SSGB, a simplified dynamic calculation model considering the effect of pounding between girder and boundary in SSGB was developed by using OpenSees earthquake simulation platform. The effects of longitudinal pounding stiffness, initial gap at expansion joint, transverse pounding stiffness, initial gap between girder and shear keys and mechanical characteristics of shear keys on the deck’s seismic inplane rotation of SSGB were analyzed. The results indicated that the longitudinal pounding stiffness, the initial gap at expansion joint and the transverse initial gap have significant effect on the deck’s seismic rotation of SSGB, while the transverse pounding stiffness has relatively unremarkable effect on the deck’s seismic rotation of SSGB; setting pads in acute angle zones at girders’ both ends in SSGB can reduce seismic rotation angle and longitudinal displacement of the girder; using elastic-plastic shear keys can control effectively the seismic inplane rotation angle of deck and mitigate the transverse force of shear keys in SSGB.
Key words:earthquake; simply-supported skewed girder bridge; deck’s inplane rotation; pounding effect; seismic response
碰撞作为地震过程中普遍发生的现象,对结构的地震反应具有重要影响,是引起结构震害的主要原因之一。中、小跨径的桥梁一般采用板式橡胶支座,在地震作用下梁体会发生显著的纵、横向位移,当相邻结构间的相对位移超过间隙宽度时将产生碰撞。与正交桥不同,地震作用下斜交桥梁体会绕竖轴发生面内转动,桥面的旋转增大了梁体的纵、横向位移,使其更易发生碰撞、落梁与支座震害。1999年墨西哥地震中某斜交桥梁体发生转动,撞击横向挡块导致挡块破坏[1];汶川地震中新东桥桥面的转动使其在锐角处发生碰撞损伤[2]。
国内外学者对斜交桥地震碰撞反应进行了大量相关研究。Maragakis等[3]发现地震引起梁体与挡块间的碰撞作用对桥面旋转影响不大;而Maleki[4]认为不考虑梁体与挡块间的碰撞可能导致不保守甚至错误的结果;何健等[5]研究了碰撞单元布置形式和碰撞刚度对连续斜交桥地震反应的影响;卢明奇等[6]研究纵向碰撞对斜交连续梁桥桥面扭转效应的影响;罗倩文[7]分析了不计阻尼影响时碰撞参数对斜交桥桥面旋转的影响。
目前在研究碰撞参数对斜交桥桥面震致转动的影响时,常将梁体与桥台间纵向碰撞、梁体与挡块间横向碰撞分开考虑,且不同学者就横向碰撞对斜交桥地震响应影响的看法不一。因此,本文根据我国斜交桥的特点,建立考虑纵、横向碰撞联合影响的斜交简支梁桥模型,研究梁体与桥台间纵向碰撞刚度、伸缩缝间隙、梁体与挡块间横向碰撞刚度、初始间隙大小、挡块的力学特性对其桥面震致转动的影响。
1动力计算模型的建立
以跨径30.0 m、桥宽12.0 m、斜度45°的装配式预应力箱梁桥为研究对象。主梁材料为C50混凝土,梁每端设置8块圆形板式橡胶支座,规格为GYZ380×80 mm,支座的剪切刚度k=4.37×103kN/m。利用OpenSees地震仿真模拟平台进行数值模拟,斜交简支梁桥上部结构采用梁杆模型简化(图1),为清晰起见,图1中未示出支座单元。主梁与横隔梁均采用弹性梁柱(Elastic Beam Column)单元模拟,梁端设置刚度较大的横隔梁;支座采用零长度(Zero Length)单元模拟。结构的阻尼比取5.0%,非线性分析时采用Rayleigh阻尼。
在斜交桥模型(图1)中利用碰撞材料(Impact Material)和零长度单元模拟梁体与刚性桥台间的纵向碰撞,利用理想塑性间隙材料(Perfectly Plastic Gap Material)和零长度单元模拟梁体与挡块间的横向碰撞,纵、横向碰撞单元均垂直布置,材料的力学模型分别如图2、3。模型中的参数:边主梁与桥台间初始碰撞刚度Kt1=5.54×105kN/m,屈后刚度Kt2=1.91×105kN/m;中主梁的Kt1=5.38×105kN/m,Kt2=1.85×105kN/m;伸缩缝初始间隙gp=5.0 cm,最大侵入深度δm=2.54 cm;梁体与挡块间的初始碰撞刚度K0=5.0×106kN/m,屈服力Fy依据文献[8]取为1 294 kN,初始间隙gap=4.0 cm。
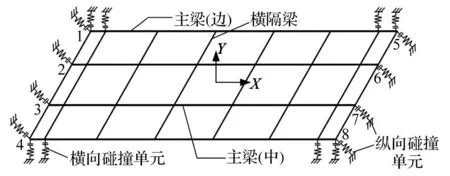
图1 斜交简支梁桥动力计算模型 Fig.1 Dynamic calculation model of simply-supported skewed girder bridge
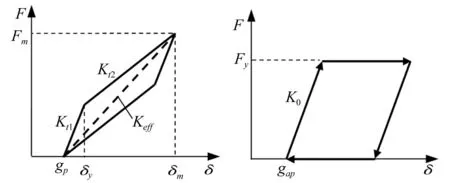

图2 纵向碰撞单元力学模型Fig.2Mechanicalmodeloflongitudinalpoundingelement图3 横向挡块力学模型Fig.3Mechanicalmodelofshearkeys
选取12条实测地震波(表1),假定地震波沿与X轴夹角26.57°方向输入(坐标系如图1),由于OpenSees中地震波只能沿坐标轴输入,因此,将地震波加速度峰值分别调整为0.4 g、0.2 g沿X轴、Y轴同时输入,以分析斜交简支梁桥的地震响应。

表1 选用的地震波
注:编号栏i-j中i代表场地类别,j代表i场地波的编号;记录台站栏中带“*”者,括号内数据为地震动记录方向。
2斜交简支梁桥桥面旋转反应的参数分析
2.1对称纵向碰撞刚度的影响
结构之间的碰撞属于复杂的非线性问题,其影响因素众多,而碰撞刚度作为碰撞分析最重要的参数之一,对结构的地震反应具有重要影响,而且取值难以准确确定[9-10]。为深入了解地震作用下纵向碰撞刚度对斜交简支梁桥桥面旋转的影响,选取5个等级的纵向碰撞刚度(表2)进行分析。
图4为4类场地波作用下斜交简支梁桥桥面转角峰值随纵向碰撞刚度的变化规律;图5给出4类场地波作用下纵向碰撞刚度对梁端纵向最大位移的影响。
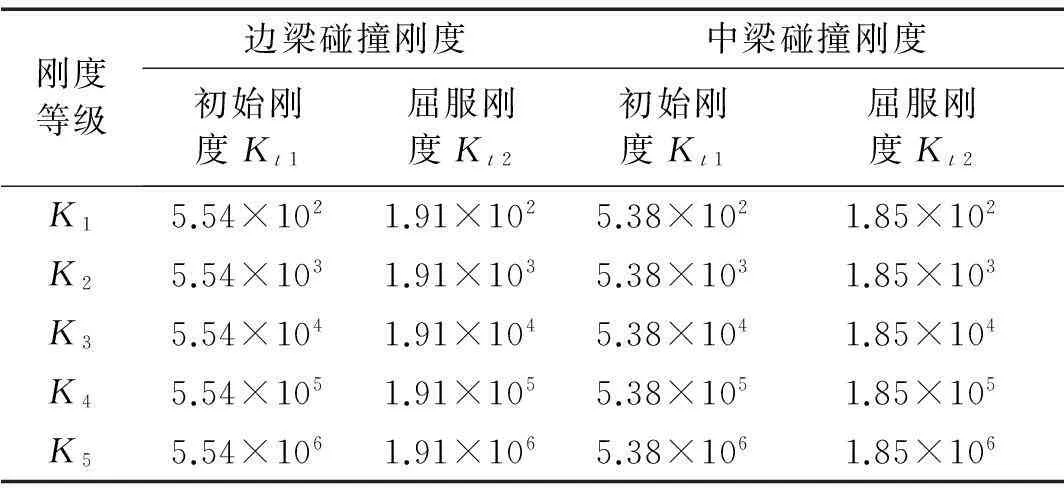
表2 不同等级的纵向碰撞刚度值 kN·m -1
由图4可以看出:地震作用下纵向碰撞刚度对斜交简支梁桥桥面转角影响较大。随着纵向碰撞刚度的增大,桥面转角峰值先增大后不变甚至有下降的变化趋势;刚度从K1增长到K3过程中,桥面的转角增长最快,最大增加9.7倍;其他阶段变化较小。由图5可知,随着纵向碰撞刚度的增大,梁端纵向最大位移逐渐减小,刚度大于K3后纵向最大位移变化不大。
2.2不对称纵向碰撞刚度的影响
通过2.1节分析可知:减小纵向碰撞刚度可有效减小斜交简支梁桥的桥面转角,但会增大梁端纵向位移。为了找到使二者均处于相对较小状态时橡胶垫块在伸缩缝处合理的布置形式,以下分6种工况分析斜交简支梁桥(图1)梁端不同部位设置橡胶垫块(减小碰撞单元的刚度视为设置垫块)对桥面转角的影响。模型中保持不变的碰撞刚度取表2中的K4,减小后的刚度取K2。
工况1:两端锐角处(角点3、4、5、6)碰撞单元刚度均减小;
工况2:两端钝角处(角点1、2、7、8)碰撞单元刚度均减小;
工况3:梁右端(角点5、6、7、8)碰撞单元刚度均减小;
工况4:4个角点处(角点1、4、5、8)碰撞单元刚度均减小;
工况5:碰撞刚度均减为K2;
工况6:碰撞刚度均不变,为K4。
其中,角点1~ 8的具体位置如图1。
计算出Ⅱ、Ⅲ类场地波作用下梁端不同部位设置垫块对斜交简支梁桥桥面转角峰值、梁端纵向最大位移的影响分别如图6、7所示。


图4 纵向碰撞刚度对桥面转角的影响Fig.4Theeffectoflongitudinalpoundingstiffnessontherotationangleofdeck图5纵向碰撞刚度对梁端纵向位移的影响Fig.5Theeffectoflongitudinalpoundingstiffnessonlongitudinaldisplacementsofdeckend 图6 不同位置设置垫块对桥面转角的影响Fig.6Theeffectofsettingpadsindifferentsitesontherotationangleofdeck
图6表明:工况1(梁端锐角处设置垫块)时桥面转角峰值要比其他工况(除工况5)都小,对减小桥面转角效果最好,工况3其次,工况2、4的影响不大;由图7可知:与工况6相比,工况1对减小梁端纵向最大位移较其他工况好,而工况2、3将增大梁端纵向位移,工况4的影响不大。由此说明:梁端锐角处纵向碰撞刚度对斜交简支梁桥桥面旋转的影响比其他位置更敏感,在锐角区设置垫块对减小斜交简支梁桥桥面转角峰值和梁端纵向最大位移均有较好的效果。
2.3伸缩缝初始间隙的影响
初始间隙作为碰撞分析另一重要参数,对结构的地震反应具有重要影响。当结构之间的相对位移大于初始间隙时,碰撞单元才开始起作用,整个体系计入碰撞刚度和阻尼,当相对位移小于初始间隙时碰撞单元不再起作用。为了探究伸缩缝间隙对斜交简支梁桥桥面旋转的影响,伸缩缝间隙gp在1.0~12.0 cm范围内取值。分析得到不同场地波作用下斜交简支梁桥桥面转角峰值均值随伸缩缝间隙的变化如图8所示。
从图8可看出,改变伸缩缝初始间隙对斜交简支梁桥桥面转角峰值的影响较大,初始间隙从1.0 cm增长到6.0 cm,桥面转角峰值增长较缓慢,而间隙从6.0 cm增长到12.0 cm,桥面转角峰值迅速减小,最多减小5.5倍。


图7 不同位置设置垫块对梁端纵向位移的影响Fig.7Theeffectofsettingpadsindifferentsitesonthelongitudinaldisplacements图8 伸缩缝间隙对桥面转角的影响Fig.8Theeffectofinitialgapatexpansionjointonrotationangleofdeck图9 横向碰撞刚度对桥面转角的影响Fig.9Theeffectoftransversepoundingstiffnessonrotationangleofdeck
2.4横向碰撞刚度的影响
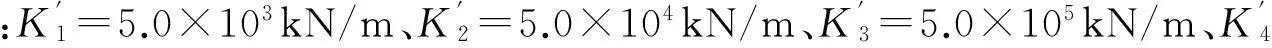

2.5梁体与挡块间初始间隙的影响
聂利英等[11]认为在横向碰撞分析时初始间隙是个不确定的影响因素。为研究地震作用下梁体与挡块间初始间隙对斜交桥桥面旋转的影响,初始间隙gap取1.0~9.0 cm进行分析。图10(a)、(b)分别为Ⅱ、Ⅲ类场地波作用下挡块间隙对锐角和钝角处挡块最大横向碰撞力的影响,图11为4类场地波作用下梁体与挡块间初始间隙对斜交简支梁桥桥面转角峰值的影响。

图10 横向间隙对碰撞力的影响 Fig.10 The influence of transverse initial gap on maximum pounding force (a) acute angle zone, (b) obtuse angle zone


图11 横向间隙对桥面转角峰值的影响Fig.11Theinfluenceoftransverseinitialgapsizeonmaximumrotationangleofdeck图12 挡块特性对最大横向碰撞力的影响Fig.12Theeffectofshearkeys’charac-teristicsontransversepoundingforce图13 挡块特性对桥面转角峰值的影响Fig.13Theeffectofshearkeys’character-isticsonmaximumrotationangleofdeck
由图10(a)、(b)可看出,随着挡块间隙的增大,挡块受到的横向碰撞力基本呈先增大后减小最后至零(不碰撞)的变化规律,由于桥面的旋转,在间隙较大时梁体先在钝角处与挡块脱开,不发生碰撞。图11表明:随着梁体与挡块间初始间隙的增大,斜交简支梁桥桥面的震致转角呈逐渐增大的趋势;初始间隙从1.0 cm增加到9.0 cm,桥面转角峰值的均值从0.0008 r/min增长到0.0035 r/min,增长了3.3倍。可见,梁体与挡块间初始间隙对斜交简支梁桥桥面转角峰值的影响较大。
2.6横向挡块力学特性的影响
为了解横向挡块力学特性对地震作用下斜交简支梁桥桥面旋转的影响,分别选取不发生破坏的弹性挡块模型和发生破坏的弹塑性挡块模型进行比较分析。其中,弹塑性挡块的模型参数取值同第1节,弹性挡块的弹性刚度K0与弹塑性挡块相同。图12、13分别给出挡块力学特性对横向最大碰撞力、桥面转角峰值的影响。
由图12可看出:设置弹性挡块要比设置弹塑性挡块时计算出的横向碰撞力大46.9%;由图13可知,设置挡块前桥面转角较大,设置挡块后桥面转角明显减小,且弹性挡块比弹塑性挡块对桥面转角的控制效果好一些,最大相差15.3%。可见,地震作用下挡块的设置能减小桥面面内转动,起到较好的横向限位作用;设置弹性挡块会增大横向碰撞力,易使与挡块相连的台帽在横向发生破坏;设置弹塑性挡块既能有效控制桥面转角,又能减小挡块的横向受力。
3结论
由于斜交桥地震反应的复杂性,严格的分析很困难,本文采用简化的动力计算模型,分析探讨了纵、横向碰撞参数对斜交简支梁桥桥面震致转动的影响,得出以下结论:
(1)纵向碰撞刚度对斜交简支梁桥桥面震致转角的影响较大,随着纵向碰撞刚度的增大,桥面转角峰值呈先增大后不变甚至有下降的变化趋势;伸缩缝初始间隙对斜交简支梁桥桥面转角峰值的影响较大,当间隙小于6.0 cm时,桥面转角增长较缓慢,当间隙大于6.0 cm时,随间隙的增长桥面转角峰值逐渐减小。
(2)横向碰撞刚度对斜交简支梁桥桥面转角的影响较小;梁体与挡块间初始间隙对桥面转角的影响较大,随初始间隙的增大桥面转角峰值逐渐增大。
(3)在斜交简支梁桥梁端锐角区设置纵向垫块对减小地震引起的桥面转角和梁端纵向最大位移有较好的效果。
(4)地震作用下挡块能减小桥面的转动,起到较好的横向限位作用,设置弹性挡块时会增大挡块的横向碰撞力,易使与挡块相连的台帽发生破坏;设置弹塑性挡块可有效减小挡块的横向受力。
(5)文中仅针对斜度为45°的装配式预应力箱形简支梁桥,在特定的地震动输入方向下,研究了纵、横向碰撞参数对斜交简支梁桥桥面震致转动的影响,具有一定局限性。今后将对不同斜度的简支梁桥,改变地震动输入方向,研究纵、横向碰撞参数对斜交简支梁桥桥面震致转动的影响规律。
参考文献
[1]Dimitrakopoulos E G. Seismic response analysis of skew bridges with pounding deck-abutment joints[J]. Engineering Structures, 2011, 33(3): 813-826.
[2]杜修力, 韩强, 李忠献, 等. 5·12汶川地震中山区公路桥梁震害及启示[J]. 北京工业大学学报, 2008, 34(12): 1270-1279.
DU Xiu-li, HAN Qiang, LI Zhong-xian, et al.The seismic damage of bridges in the Wenchuan earthquake and lessons from its damage[J]. Journal of Beijing University of Technology, 2008, 34(12): 1270-1279.
参考文献
[3]Maragakis E A, Jennings P C. Analytical models for the rigid body motions of skew bridges[J]. Earthquake Engineering & Structural Dynamics, 1987, 15(8): 923-944.
[4]Maleki S. Seismic modeling of skewed bridges with elastomeric bearings and side retainers[J]. Journal of Bridge Engineering, 2005, 10(4): 442-449.
[5]何健, 叶爱君. 连续斜交梁桥地震下碰撞效应分析[J]. 中南大学学报, 2012, 43(4): 1475-1481.
HE Jian, YE Ai-jun. Seismic response of continuous skew bridges with pounding effect[J]. Journal of Central South University, 2012, 43(4): 1475-1481.
[6]卢明奇, 杨庆山, 李英勇. 地震作用下斜交连续梁桥碰撞效应分析[J]. 中国矿业大学学报, 2012, 41(2): 289-292.
LU Ming-qi, YANG Qing-shan, LI Ying-yong. Collision effect analysis of skew continuous bridge under seismic response[J]. Journal ofChina University of Mining & Technology, 2012, 41(2): 289-292.
[7]罗倩文. 斜交梁桥抗震性能计算分析研究[D]. 重庆: 重庆交通大学, 2012.
[8]Silva P F, Megally S, Seible F. Seismic performance of sacrificial exterior shear keys in bridge abutments[J]. Earthquake Spectra, 2009, 25(3): 643-664.
[9]高玉峰, 蒲黔辉, 李晓斌. 考虑碰撞效应的双柱式高墩桥梁非线性地震反应特性研究[J]. 公路交通科技, 2011, 28(4): 36-45.
GAO Yu-feng, PU Qian-hui, LI Xiao-bin. Nonlinear seismicresponse characteristics of bridge with double-column high-rise piers considering pounding effect[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 36-45.
[10]邓育林,雷凡,何雄君. 纵向地震作用下大跨三塔悬索桥伸缩缝处双边碰撞效应研究[J]. 振动与冲击, 2013,32(12):126-130.
DENG Yu-lin, LEI Fan, HE Xiong-jun.Effect of double-side pounding at expansion joints on seismic response of a long-span triple-pylon suspension bridge[J]. Journal of Vibration and Shock, 2013,32(12):126-130.
[11]聂利英, 李建中, 范立础. 地震作用下结构碰撞的模型参数及其影响分析[J]. 工程力学, 2005, 22(5): 142-146.
NIE Li-ying, LI Jian-zhong, FAN Li-chu. Selection of pounding analysis parameters and its effects on structure under earthquake[J]. Engineering Mechanics, 2005, 22(5): 142-146.


