基于 Layerwise 理论的共固化粘弹阻尼复合材料动特性分析

2016-01-12徐超,林松,王立峰等

振动与冲击 2015年1期

基于Layerwise理论的共固化粘弹阻尼复合材料动特性分析

徐超1，林松1，王立峰2，王建月2

(1.西北工业大学航天学院，西安710072；2. 航天材料及工艺研究所，北京100076)

摘要：共固化粘弹性复合材料兼具结构承载和阻尼减振功能。针对传统的混合单元法在应用于粘弹性夹层复合材料结构阻尼性能分析时存在着前处理困难、计算规模大、精度低以及难以考虑正交各向异性铺层自身损耗能力的缺点，推导了一种基于Layerwise离散层理论的四节点四边形复合材料层合板单元，并利用直接复特征值解法建立了共固化粘弹性复合材料结构的阻尼性能分析方法。将该方法应用于不同的阻尼结构，分析结果与文献中已公开结果和混合单元法的计算结果进行了对比验证。结果表明，基于离散层理论的层合板单元具有计算精度高、前处理建模简单和计算规模小的优点，可有效应用于复杂共固化粘弹性复合材料结构的阻尼性能分析和设计。

关键词：粘弹性；复合材料；离散层理论；有限元

中图分类号:V414文献标志码：A

基金项目：中国博士后科学基金面上资助项目(2013M530192); 上海市博士后科研资助项目(12R21413800)

收稿日期：2013-11-18修改稿收到日期：2014-01-02

Layerwise dynamic analysis of composite laminates with co-cured viscoelastic damping layers

XUChao1,LINSong1,WANGLi-feng2,WANGJian-yue2(1. School of Astronautics, Northwestern Polytechnical University，Xi’an 710072, China； 2. Aerospace Research Institute of Material and Processing Technology，Beijing 100076，China)

Abstract:The Co-curing of thin viscoelastic damping materials in the composite laminates can improve their structural damping with less loss of stiffness and strength. However, classic numerical simulation of the damped structures by using hybrid finite element method demands a cumbersome computational work, especially for complicated layered structures. A new 4-node quadrangular plate finite element based on the discrete layerwise plate theory was developed for dynamics analysis of composite laminates with co-cured viscoelastic layers. The natural frequencies and modal loss factors of different viscoelastic damped laminated beams, cylindrical shells and stiffened plates were derived. The results show that the proposed model can correctly describe the high shear pattern developed inside thin viscoelastic layers and provide results with less computational work.

Key words:viscoelasticity; damped composite; discrete layerwise theory; finite element analysis

先进纤维增强复合材料因其突出的比强度、比刚度和可设计性强等优点，已成为航空、航天飞行器的一种主要结构材料。复合材料自身的损耗因子比金属材料高约1~2个数量级，但其作为结构使用时，多采用整体化成型工艺制造，因而装配结合面大为减少，界面摩擦损耗能力减弱，整体结构阻尼值并不高，在实际使用中仍显偏低[1]。共固化粘弹性复合材料是一种新型的结构阻尼复合材料。所谓共固化，是指在纤维增强复合材料成型工艺过程中，将高分子粘弹性材料作为特定的铺层嵌入层合结构中去，然后共同固化成型[2]。它的最大特点是经过共固化处理，粘弹性阻尼材料与结构复合材料合为一体，既充分利用了粘弹性材料的高损耗能力，又不显著降低复合材料的刚度和强度性能，还能利用复合材料的可设计性进行“事前”阻尼设计，达到了结构承载和阻尼减振功能一体化的目的。

一般说来，粘弹性阻尼材料的模量较复合材料铺层低约4~5个数量级，作为夹层嵌入层合结构中后，受到相邻刚度较大的弹性层变形约束，发生剪切变形，通过分子链段间的摩擦耗散振动能量。分析共固化粘弹性复合材料的阻尼性能必须要考虑阻尼层的剪切变形以及沿厚度方向材料的不均匀性。通用有限元软件中的层合板、壳等结构单元多是基于经典层合板理论或一阶剪切变形理论，前者忽略了层合板的横向剪切变形，而后者未能考虑横向剪切变形沿板厚方向分布的不均匀性，忽略了粘弹性材料层高剪切变形的事实，因而都不能很好的用于共固化粘弹性复合材料阻尼性能的分析[3]。目前，工程中一般采用“混合单元法”进行阻尼结构的分析和设计[4-6]，即采用三维实体单元描述阻尼层的剪切变形，采用传统的层合板壳单元描述复合材料弹性层，板壳单元和实体单元之间通过定义节点偏置或多点约束方程相联系。张少辉等[4]对复合材料弹性层也采用实体单元模拟，应用全三维实体模型和模态应变能法分析了共固化粘弹性复合材料结构的损耗因子。徐超等[5]应用混合单元法对卫星飞轮支架进行了共固化阻尼减振设计。林松等[6]应用混合单元法和多目标遗传算法建立了共固化粘弹性复合材料的阻尼/结构一体化设计方法。混合单元法在实际应用中主要存在三大不足：一是随着阻尼层数增多，有限元模型规模骤增，建模前处理困难，计算耗费巨大；二是阻尼层厚度较小，体单元长厚比大，计算误差较大；三是修改阻尼层厚度或插入位置时需要进行有限元网格重构，不易于进行优化设计。

Reddy[7]提出的Layerwise离散层理论是描述复合材料层合结构力学行为的精细理论。基于Layerwise理论的结构单元已被成功用于层间应力计算、损伤预测等复合材料力学问题中。它在统一的位移场描述下，独立地考虑各层的变形，并通过引入层间位移连续性假设，将三维问题退化为二维问题，计算建模简单，易于进行优化设计。文献[8]基于Layerwise理论推导了多层阻尼梁单元的有限元列式，分析了共固化粘弹复合材料平面梁的阻尼性能。本文基于Layerwise板理论，推导一种四节点四边形等参数板单元，将其应用于共固化粘弹性复合材料层合结构固有频率和阻尼性能的分析，并通过与文献中已有结果和传统分析方法的对比验证方法的有效性。

1基于Layerwise理论的复合材料层合板单元

根据Reddy的Layerwise理论，首先将复合材料层合结构沿厚度方向分为若干层。各层既可以是真实物理材料层，也可以是由多个材料层构成的等效层或者把单层材料再离散的数学意义上的数值层等。为准确分析复合材料结构的阻尼性能，要把嵌入的各粘弹性材料层划分为单独层。然后将划分后的每一层视作考虑面内、弯曲和横向剪切变形的Mindlin板，且各层之间满足位移连续条件[9]。基于Layerwise理论推导有限元单元时，引入如下计算假设：①忽略层板横向正应变的影响；②各层内材料均匀，且符合线弹性或线粘弹性假设；③考虑各层的平动质量和转动惯量。

1.1位移场

如图1所示，将层合板沿厚度方向划分为n层，各层厚度为hk(k=1，…n)。取k=1层中面所在平面为参考面，建立正交坐标系oxyz，其中z轴沿板厚度方向，oxy位于参考平面内，u，v，w分别为各层沿坐标轴方向的位移，θx，θy分别为各层法线绕x，y轴的转角，zk[-hk/2，hk/2]为各层z向的局部坐标。

图1　Layerwise板的位移场 Fig.1 Displacement field of the Layerwise plate

按照Layerwise理论和计算假设(1)，复合材料层合结构中第k(k≥2)层的位移场{u}k为

{u}k=

(1a)

第k=1层的位移场与通常的Mindlin板相同，即

(1b)

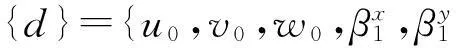
(2)

这样，第k层的位移场可记为

{u}k=[N]k{d}

(3)

式中，矩阵[N]k为

[N]k=

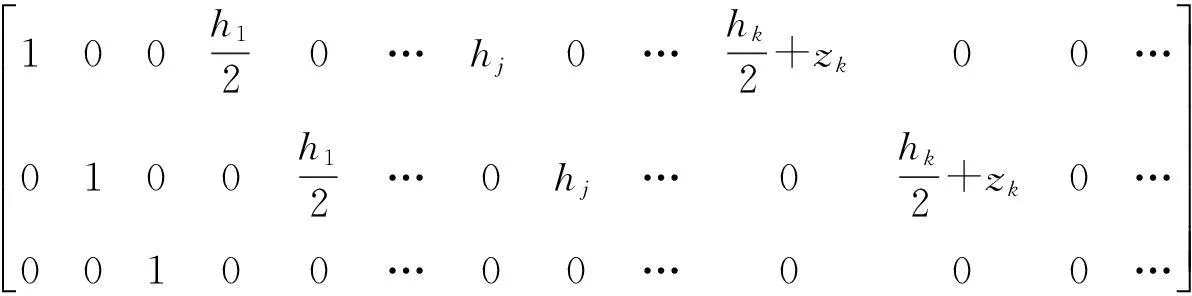
1.2应变场

(5)

其中，

式中，M、C、B和S分别表示膜(membrane)、耦合(coupling)、弯曲(bending)和横向剪切(transverse shear)应变项。

因此，各层的应变场可表示为

(7)

(8)

(9)

即重新排列后的应变可表示为

{ε}k=[B]k{d}

8×18×(2n+3)(2n+3)×1

(10)

1.3应力场

仍按式(8)的排列形式，根据应力-应变物理方程和假设(2)，应力场{σ}k为

{σ}k=[D]k{ε}k

8×18×88×1

(11)

式中，[D]k为物理矩阵。

对于各向同性不可压粘弹性阻尼材料，通常采用复模量模型描述其本构关系，即材料弹性模量为

E*=E(1+jβ)

(12)

1.4应变能和动能

层合结构的应变能表示为各层应变能的叠加，利用式(10)和式(11)，在待求域Ωk上积分可得

(13)

层合结构的动能可表示为各层动能的叠加，即

(14)

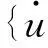
(15)

1.5四节点四边形等参数板单元

由式(3)可知，广义位移场为二维坐标x,y的连续函数。为求得广义位移场，按照有限元法基本思想，将求解域离散化为四边形等参数单元组成的有限元计算模型，每个单元有四个节点，如图2所示，其位移插值函数和等参坐标变换函数均为[10]

(i=1,...,4)

(16)

将每个单元节点处参考平面上3个平动位移和各层法线绕坐标轴的转角取为节点位移，则每个单元节点自由度的数目为4×(2n+3)=8n+12。可见，单元层数分的越多，单元矩阵的维数就越大。

图2　四节点等参单元局部与参数坐标系 Fig. 2 Local and natural coordinate system of 4 node quadrilateral element

(17)

进一步，将式(17)代入式(13)和式(15)，并在单元子域上计算，可得单元应变能和动能的表达式，再应用Hamilton原理，最终可得单元刚度矩阵和质量矩阵分别为

(18)

(19)

其中，[B]k是单元第k层的几何矩阵

[B]k=[B]k[N]

(20)

[J]k是单元第k层的一致惯性矩阵

[J]k=ρk[N]Tk[N]k

(21)

2系统运动方程

式(18)、(19)定义的单元刚度矩阵和质量矩阵是定义在单元坐标系下的，将其进行坐标变换至结构整

体坐标系下，并组装可得系统自由振动的运动微分方程为

(22)

式中，[M]为总体质量矩阵，[K]为总体刚度矩阵，{di}为结构全局节点自由度向量。

(23)

(24)

本文用Matlab编写了相应有限元求解程序，并采用eigs函数直接求解式(22)的复特征值问题[11]。

3数值验证和结果分析

3.1粘弹性阻尼夹层悬臂梁

为验证本文的分析方法和程序，以文献[12]给出的粘弹性阻尼夹层悬臂梁解析模型为对象，该梁平面尺寸为177.8 mm×25.4 mm，上、下弹性层及阻尼夹层的厚度及材料参数见表1所示。

表1　粘弹性阻尼夹层梁材料参数

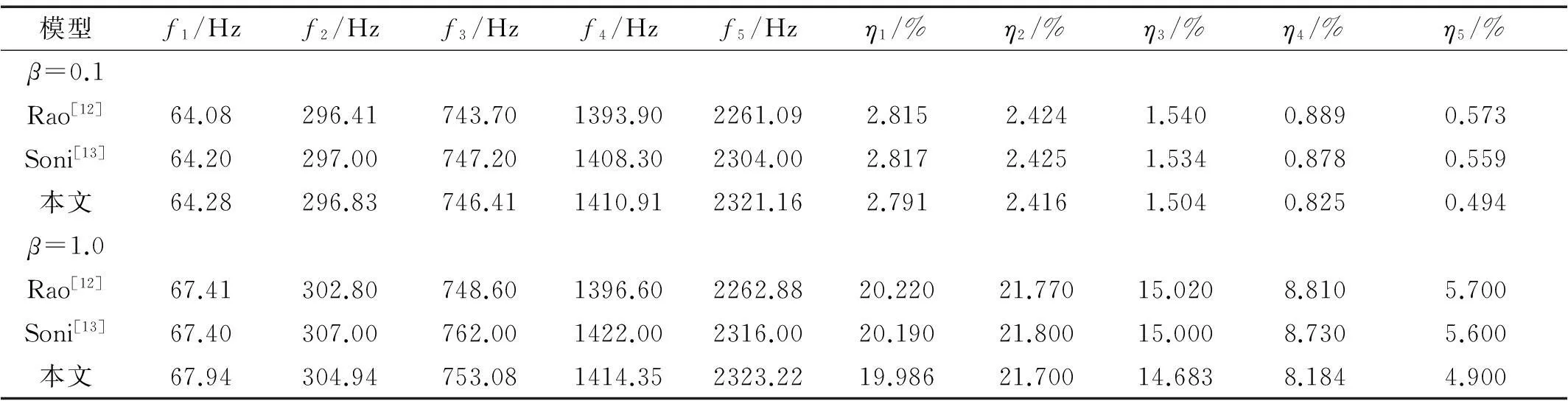
表2　粘弹性阻尼夹层悬臂梁固有频率和损耗因子

采用本文的Layerwise板单元和分析方法，将夹层梁用四边形板单元离散，长度方向单元数14，宽度方向为2，厚度方向离散为3层。表2给出了针对该模型的六阶梁理论解析解[12]，文献[13]采用三维实体单元建模的有限元解以及本文的分析结果。

由表2可知，无论在粘弹性阻尼材料低损耗因子还是高损耗因子的情况下，基于Layerwise理论的板单元都能准确描述阻尼材料的剪切变形和结构的动刚度特性，所给出的固有频率和模态损耗因子的计算结果都与文献中已公开结果符合很好，说明本文单元和分析方法可以用于分析粘弹性阻尼夹层结构的固有频率和阻尼特性。

3.2共固化粘弹性复合材料层合圆柱壳

分析文献[14]中的共固化粘弹性复合材料层合圆柱壳的阻尼性能。圆柱壳体的几何尺寸如图3所示。壳体固支ABCD面，铺层为[(02/902)/V/(902/ 02)]，其中V表示粘弹性阻尼层。正交各向异性铺层单层厚度为0.25 mm，计算时同时考虑复合材料自身的损耗能力，具体材料参数为：E1=119 GPa，E2=8.67 GPa，μ12=0.31，G12=G13=5.18 GPa，G23=3.9 GPa，ρ=1 570kg/m3，η11=0.118%，η22=0.620%，η12=η13=0.812%，η23=0.846%。

粘弹性阻尼材料层厚度为0.25 mm，材料参数为：E=4.25 MPa,ν=0.49,ρ=968.8 kg/m3,β=1.56。

图3　共固化粘弹性复合材料层合圆柱壳几何尺寸 Fig.3 Geometry and configuration of cylindrical composite blades with co-cured viscoelastic layer

表3　共固化粘弹性复合材料圆柱壳固有频率和损耗因子

取Layerwise板单元网格密度为16×8，厚度方向离散为3层，其中粘弹性阻尼材料层为单独层，上下层合板分别考虑为等效层。表3给出了无阻尼层和共固化粘弹性复合材料层合圆柱壳固有频率和模态损耗因子的计算结果，并与文献[14]，以及传统的采用混合单元法建模使用MSC.NASTRAN直接复特征值分析(SOL107)得到的结果进行了对比。

需要注意的是，圆柱壳为曲面壳体，采用混合单元法建模时，等效板单元节点偏置定义需保证其沿当地曲面的法线方向，而这对复杂曲面壳体而言非常繁琐。采用layerwise板单元时，只需将参考面按通常的平面单元离散，各层的位置和材料属性转化为物理参数输入，从而大大简化了前处理的过程，这对复杂形状结构和嵌入多阻尼层的情况是极方便的。此外，通用有限元软件中往往不支持考虑复合材料自身各向异性的损耗能力，而在Layerwise板单元，可将各层的弹性系数都考虑为复刚度形式，从而能够有效的计算复合材料自身的损耗能力。

由表3结果可知，只考虑复合材料自身损耗能力的情况下，本文计算的前四阶模态的固有频率和损耗因子的结果与文献[14]都符合很好，证明了Layerwise平板单元模拟曲面壳体动态特性的能力。共固化粘弹性阻尼材料层后，结构各阶模态固有频率变化不大，但模态损耗因子却增大了约1个数量级，表明嵌入阻尼层能显著增大复合材料层合结构的阻尼性能。对比嵌入阻尼层后的损耗因子分析结果，本文的计算结果与SOL107解法获得的结果较符合，但与文献[14]的差别近1倍。这主要是因为文献[14]是采用的模态法求解结构阻尼特性，而在此过程中，需要用到无阻尼结构的振型矩阵以进行物理空间和模态空间的坐标变换。在材料损耗因子较小的情况下，无阻尼结构的实特征值解与有阻尼结构的复特征值解差别较小，而在大损耗因子的情况下，这种近似则可能会导致较大的误差。为进一步验证上述结论，使用MSC.NASTRAN的模态复特征值解法(SOL110)分析算例问题，结果也列于表3中。可见，使用SOL110求解序列获得结果与文献[14]吻合的很好，从而说明本文计算结果与文献[14]的误差主要是由于所采用的复特征值解法不同造成的。进一步结合3.1节中与解析解的比对可知，模态解法通常仅适用于材料损耗因子较低的情况，在材料高损耗因子的情况下，直接法获得的结果更为可信[15]。

3.3共固化粘弹性复合材料加筋板

加筋板是航空航天飞行器上广泛采用的薄壁结构形式。考虑一四边简支的复合材料加筋板，面板尺寸为500 mm×450 mm，面板铺层为[0/45/-45/90/V/90/-45/45/0]T，其中V表示粘弹性材料阻尼层，单层铺层厚度为0.2 mm；沿长度方向有两对称分布筋条，间距为150 mm，高度为20 mm，筋条全为0度铺层，总厚度为2 mm。各向异性铺层材料属性与3.2中相同。分别计算阻尼层厚度tv=0，0.2 mm, 0.5 mm时加筋结构的阻尼性能。取Layewise板单元模型网格密度为25×24，厚度方向分为3层。

需要注意的是，对于复杂复合材料阻尼结构，混合单元法中采用三维实体单元模拟阻尼层，采用基于经典层合板理论的普通板单元模拟弹性层以及筋条，两者之间需定义多点约束方程进行连接，前处理过程较为繁琐；而采用Layerwise板单元时，只涉及四边形板单元，可按传统的板单元建模方法构造模型。而且，两者模型形成的计算规模也有差别，阻尼层厚度较薄时，为了减小实体单元的长厚比(本例中取10：1)，网格密度需取得很密，结构矩阵维数很高，而Layerwise板单元在较疏的网格密度下就可取得满意的精度。从面向优化设计应用的角度看，使用混合单元时，若修改阻尼层厚度，需要改变实体单元节点坐标，导致有限元网格的重构；而使用Layerwise板单元时，阻尼层的材料参数和各层厚度都是物理参量，对它们进行修改时与有限元网格无关，大大方便了优化设计。

表4　复合材料加筋阻尼板固有频率和损耗因子

表4中对比了本文的分析结果与采用MSC.NASTRAN混合单元法分析的结果。由表4可知，当tv=0时，本文的分析结果与NASTRAN的分析结果非常符合，并且本文的分析还能给出仅考虑正交各向异性铺层损耗因子时的复合材料结构的阻尼性能。当tv=0.2 mm和0.5 mm时，随着阻尼层厚度的增大，各阶模态的固有频率下降，损耗因子显著增大，两类方法预测的阻尼值和变化规律都一致，再次证明了本文方法的有效性。

4结论

本文利用Layerwise离散层理论推导了可用于共固化粘弹性层合结构阻尼性能分析的四节点四边形等参数板单元，应用该单元分析了典型粘弹阻尼结构的固有频率和模态损耗因子，并与文献已公开结果和传统分析方法进行了对比验证。结果表明：

(1)基于Layerwise理论构造的复合材料层合板单元能够正确描述阻尼层的高剪切变形，计算精度好且能够考虑各向异性弹性层自身的损耗能力，可应用于共固化粘弹性复合材料结构性能的分析。

(2)相比于传统的混合单元法，应用本文的层合板单元对复杂阻尼结构进行分析，能够大大简化前处理建模过程，计算规模也较小。

另外，采用层合板单元避免了传统方法在铺层顺序或阻尼夹层厚度改变时需要重构有限元往网格的问题，可方便的推广于粘弹性阻尼复合材料结构/阻尼的一体化设计。

参考文献

[1]Finegan I C, Gibson R F. Recent research on enhancement of damping in polymer composites [J]. Composite Structures, 1999, 44: 89-98.

[2]余启勇，马玉璞，郭万涛，等. 结构阻尼复合材料及其研究进展[J]. 材料工程, 2007(S1): 253-258.

YU Qi-yong，MA Yu-pu，GUO Wan-tao，et al. Structural damping composite and its research progress[J]. Journal of Materiale Engineering,2007, (S1):253-258.

[3]Carrera E, Brischetto S. A survey with numerical assessment of classical and refined theories for the analysis of sandwich plates [J]. Applied Mechanics Reviews, 2009, 62:301-316.

[4]张少辉，陈花玲. 共固化复合材料粘弹阻尼结构的损耗因子研究[J]. 航空材料学报，2005, 25(1): 53-57.

ZHANG Shao-hui, CHEN Hua-ling. Damping analysis of cocured composites with interleaved viscoelastic layers [J]. Journal of Aeronautical Materials,2005, 25(1): 53-57.

[5]徐超，李瑞杰，游少雄. 卫星飞轮支架的共固化阻尼减振设计[J]. 宇航学报, 2010, 31(3):907-911.

XU Chao, LI Rui-jie, YOU Shao-xiong. Passive vibration control design with co-curing damping composite for a satellite flywheel bracket [J], Journal of Astronautics, 2010, 31(3):907-911.

[6]林松，徐超，吴斌. 共固化粘弹性复合材料的结构多目标优化设计[J]. 宇航学报, 2010, 31(8): 1900-1905.

LIN Song, XU Chao, WU Bin. Multi-objective evolutionary optimization design of composite structure embedded with cocured viscoelastic layers [J]. Journal of Astronautics, 2010, 31 (8):1900-1905.

[7]Reddy J N. Mechanics oflaminated composite plates: theory and analysis. Boca Raton: CRC Press, 1997.

[8]徐超，张醒，李瑞杰，等. 多粘弹性胶膜夹层约束阻尼梁损耗因子分析[J]. 宇航学报, 2009, 30(2): 458-462.

XU Chao, ZHANG Xing, LI Rui-jie, et al. Modal loss factor analysis for sandwich beams embedded with multiple viscoelastic damping thin layers[J]. Journal of Astronautics, 2009, 30(2): 458-462.

[9]Moreira R A S, Rodrigues J D. A Layerwise model for thin soft core sandwich plates [J]. Computers and Structures, 2006, 84: 1256-1263.

[10]Cook R D, et al. 有限元分析的概念与应用[M]. 关正西，强洪夫译.西安：西安交通大学出版社，2007:176-179.

[11]MATLAB Version R2009a. The Math Works Inc: Natick, U.S.A., 2009.

[12]Rao D K. Frequency and loss factors of sandwich beams under various boundary conditions [J]. Journal of Mechanical Engineering Science,1978, 20: 271-282.

[13]Soni M L,Bogner F K. Finite element vibration analysis of damped structures [J]. AIAA Journal,1981, 20(5): 700-707.

[14]Oh Il-Kwon. Dynamic characteristics of cylindrical hybrid panels containing viscoelastic layer based on Layerwise mechanics [J]. Composites Part B: Engineering,2007,38(2):159-171.

[15]Torvik P J, Runyon B. Modifications to the method of modal strain energy for improved estimates of loss factors for damped structures [J]. Shock and Vibration, 2007, 14:339-353.

《振动与冲击》入选中国精品科技期刊

近日，国家科技部中国科学技术信息研究所公布第3届中国精品科技期刊遴选结果和2014 年度“领跑者5000——中国精品科技期刊顶尖论文(F5000)”收录情况。《振动与冲击》作为中国精品科技期刊顶尖学术论文(F5000)项目来源期刊，有20篇论文入选F5000。自2012年以来，《振动与冲击》共有50篇论文被评为F5000论文。

中国精品科技期刊顶尖学术论文(F5000)是由中国科学技术信息研究所于2012年底启动，每年评选一次。中国科学技术信息研究所从300多家中国精品科技期刊近5年发表的论文中评选出“领跑者5000——中国精品科技期刊顶尖学术论文”，以集中展示和交流我国的顶尖学术论文。通过“领跑者5000——中国精品科技期刊顶尖学术论文平台(F5000)”与国际和国内重要检索系统链接，并利用WOK国际检索平台与SCI数据库在同一平台内实现链接和国际引文检索，向世界和科技界同行展示和推广我国最重要的科研成果，扩大中国学术期刊和出版机构的国际影响。