人－桥动力相互作用下侧向振动的动力放大系数分析

人-桥动力相互作用下侧向振动的动力放大系数分析

宋志刚，张尧

(昆明理工大学土木工程学院，昆明650500)

摘要：从社会力模型和人桥相互作用的机理出发研究了柔性人行桥在人桥相互作用下侧向振动的动力放大系数。首先将人行激励分解为固有侧向力和附加侧向力，分别采用傅里叶级数模型和社会力模型表示上述侧向力，从而建立考虑负阻尼的强迫振动模型。结合该模型推导出动力放大系数的表达式，在此基础上给出了基于动力放大系数的结构动力响应的简化计算方法。最后，结合某人行桥结构，对比分析了采用建议的估算方法与时程模拟结果的差异，证实了简化计算方法的有效性。

关键词：人行桥；侧向振动；人桥相互作用；动力放大系数；动力响应估算

中图分类号:TU311.2; TU112.2文献标志码：A

基金项目：国家自然科学基金(11132002，10972014);优秀博士培育基金( YB20091000502);内蒙古农业大学科技创新团队计划项目(NDTD2013-6)

收稿日期：2013-08-20修改稿收到日期：2013-12-19

Analysis of the dynamic amplification factor of latetral structural vibration induced by crowd-bridge interaction

SONGZhi-gang,ZHANGYao(Department of Civil Engineering, Kunming University of Science & Technology, Kunming 650500, China)

Abstract:Depending on the social force model and the mechanism of crowd-bridge interaction, the lateral dynamic amplification factor of flexible footbridges was studied. The lateral step force induced by pedestrian was divided into two parts, namely the intrinsic lateral force and additional lateral force. Representing the two parts of forces by Fourier series and social force respectively, the motion equation of footbridge was set up with the consideration of negative damping. The expression of dynamic amplification factor was derived from the structural motion equation. Then a simplified method for estimating structural responses was proposed according to the relationship between structural responses and the dynamic amplification factor. The peak displacement and acceleration of a concrete footbridge were calculated by using the simplified method and the conventional time history analysis respectively. The results of the two methods were compared with each other, and the effectiveness of the simplified method was validated.

Key words:footbridges; lateral vibration; crowd-bridge interaction; dynamic amplify factor; dynamic response estimation

大跨人行桥人致侧向动力失稳问题引起了广泛关注。在英国伦敦千禧桥[1-2]和日本T桥[3-4]等一些大跨人行桥上均观测到了人桥相互作用引起的过大侧向振动。Dallard等[1-2]和Nakamura等[3-4]分别在对千禧桥和T桥的观测和实验基础上提出了带有经验参数的负阻尼模型，解释了人行桥结构侧向动力失稳的原因，并推导出失稳时的临界人数表达式。Roberts[5]由行人的人体侧向运动方程推导出人桥相互作用力，提出了理论模型。Newland[6]将人桥相互作用力分为两部分，分别由行人和桥面运动产生。

根据以上负阻尼理论的基本思想，本文针对低密度人群过桥情况，提出了考虑人桥相互作用的负阻尼模型。低密度稳态人流过桥时，人群中每个行人都有足够的行走空间，其步频和步幅不受周围其他行人影响，可以忽略人-人相互作用。行人侧向步行力使结构产生强迫振动，引起了行人行走路线的改变，与之对应的人体重心移动反过来又导致了行人侧向步行力的改变。因此，本文将行人侧向步行力划分为两部分。一部分称作固有侧向力，由行人在固定桥面上行走产生，另一部分称为附加侧向力，即上述人体重心移动所引起的侧向力改变量。固有侧向力可运用傅里叶级数近似表示，附加侧向力可通过社会力模型表示为负阻尼力，从而可以建立用于振动分析的负阻尼模型。继而由该模型推导出结构侧向振动的动力放大系数表达式。

1侧向力模型

1.1侧向步行力划分

本文以简支梁作为大跨人行桥的计算模型。设一人行桥质量沿桥长均匀分布，单位长度内为mb，且阻尼和侧向抗弯刚度沿桥长为定值，分别为c和EI。人行激励作用下结构的运动方程为

(1)

式中，w表示侧向挠度，xi0、vi和pi(x,t)分别为行人i的初始位置、行走速度和步行力函数，δ(·)为单位脉冲函数，形式为：

(2)

行人在振动桥面上行走时，身体重心的移动可分为两部分，一部分由左右脚交替引起，另一部分由桥面运动引起，如图1实线所示。与之对应将(1)式中行人i的侧向步行力分为两部分

pi(x,t)=pii(t)+pia(x,t)

(3)

pii(t)和pia(x,t)分别称为固有侧向力和附加侧向力。

图1　运动桥面上行人重心的移动 Fig.1 Body gravity centre movement on vibrating deck

1.2固有侧向力

图2　运动表面上 期望速度方向的偏转 Fig.2 Desired velocity deflection on vibrating deck

在固定桥面上行人行走路线为直线。固有侧向力即由重心在左右脚之间交替移动所产生。本文以傅里叶级数作为固有侧向力模型[7]，其表达式为

pii(t)=

(4)

式中，Wi为行人i的体重，fi为侧向步频，亦即0.5倍步频，这里假设行人的质量为70 kg，侧向步频服从均值为0.925Hz，标准差为0.075的正态分布，k表示步行力谐波阶数，DLFk为第k阶谐波动荷因子，θik为行人i的k阶谐波相位。取前五阶谐波，各阶谐波动荷因子按文献[7]的实验结果取值，见表1。并且认为θik服从[0,2π]的均匀分布。

表1　固有侧向力前五阶谐波动荷因子

1.3附加侧向力

在振动桥面上，行人重心随桥面运动而移动(如图1虚线所示)。附加侧向力由该部分重心移动所产生，其表达式通过社会力模型推导获得。

Helbing等[8]提出的社会力模型，在模拟人群运动行为中有广泛应用。根据社会力模型，可将人群看作若干个体组成的多体动力系统，其中每个行人受到三种作用力，分别为行人朝目标区域行进的驱动力、周围其他行人对其产生的社会力、以及周围边界(或障碍物)对其产生的边界力。以上三种力服从牛顿第二定律，于是行人i的受力平衡方程为

(5)

式中，mi、vi(t)为行人i的质量和运动速度矢量，Fij为行人j施加给i的社会力矢量，Fiw为边界(或障碍物)w施加给i的边界力矢量，Fi为行人i的驱动力矢量。假设在低密度人群中,每个行人都有足够的自由行走空间，其行走速度和步态不受周围行人或边界(障碍)影响，故忽略式(5)等号右边的后两项得

(6)

驱动力矢量的表达式为

(7)

式中，voi为行人i的期望速率，e(t)为期望矢量方向，τ为张弛时间，表示行人对桥面运动做出反应的时间，其值可取0.42 s[8]。现假设行人i位置x处的桥面以速度vb(x,t)发生侧向振动，此时行人为调整重心以保证原有的运动方向，其期望矢量方向会随桥面运动而发生偏转，如图2所示。根据矢量合成法则，式(7)可写为，

(8)

根据作用力与反作用力原理，桥面所受该力的反作用力即为附加侧向力。考虑结构侧向振动位移与速度的微分关系，可将附加侧向力表达为

(9)

式(9)中结构振动速度方向与位移方向相同，于是改为标量表示。

2动力放大系数推导

将式(4)和式(9)代入运动方程(1)，并引入广义坐标，

(10)

式中,φj表示第j阶振型，Zj为广义位移。将式(1)解耦得到

(11)

式中，ξj为广义阻尼比，Mj、Fj和ωj为广义质量、人行激励函数和结构自振频率，表达式分别为式(12)~式(14)。

(12)

(13)

(14)

以上各式中，φj(4)表示振型对x的四阶导函数，L为桥长，g为重力加速度，其他符号意义同上。稳态人流(人流密度稳定)通过人行桥时，行人均匀地分布于桥面，且以稳定的速度前进，此时前方行人的位置将马上被他身后的行人占据。若忽略行人间年龄、性别等差异，则该情况下行人作用于结构的总侧向步行力与他们原地踏步时的侧向步行力等价[9]。于是可假设行人的位置不变，略去Fj表达式中的vit项，同时假设行人质量沿桥长均匀分布。式(13)简化为

(15)

将式(15)代入式(11)，经移项化为

(16)

根据文献[9]，梁式结构的动力响应主要由一阶振型支配，且受支撑条件影响较小，故令φ1=sin(πx/L)，并分别代入式(16)，(12)，(14)，整理得

(17)

(18)

(19)

(20)

令rN=N/Ncr，即桥上实际行人数与临界人数比，于是有

(21)

代入(17)式得

(22)

由式(22)可知，固有侧向步行力k阶波作用下结构的运动方程为

(23)

根据单自由度体系在简谐荷载作用下的动力响应[10]，步行力k阶波作用下结构的位移幅值为

(24)

(25)

(26)

式中,β为行人侧向步频与结构自振频率之比。

(27)

结构稳态响应可表达为步行力各阶谐波作用下的响应叠加，

(28)

(29)

(30)

定义D为结构的等效动力放大系数，其值为结构总位移幅值除以大小为步行力一阶谐波幅值的静荷载作用于结构所产生的静位移。

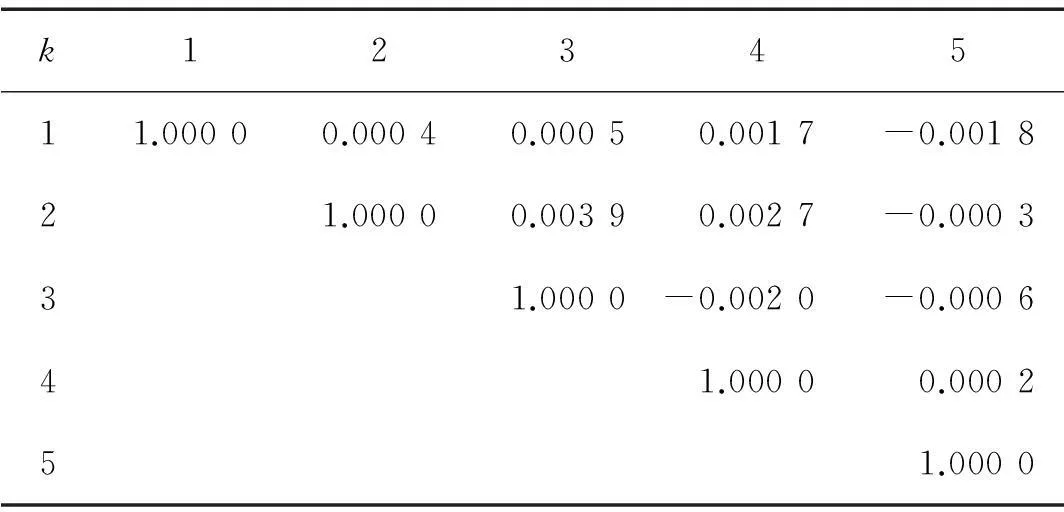
表2　各阶谐波峰值响应的相关系数

3考虑人-桥相互作用的动力响应估算方法

由式(26),(27)和(30)可知，动力放大系数主要受结构自振频率ω1、阻尼比ξ1和桥上行人数量比rN三个参数影响。对于某一人行桥，其ω1和ξ1为定值，人桥相互作用对结构动力放大系数的影响由rN决定。于是可将动力放大系数看作是以rN为自变量的函数，表示为D(rN)，根据上述负阻尼理论，D(0)表示不考虑人桥相互作用的动力放大系数。

由式(29)可知结构位移响应峰值与动力放大系数成正比，动力放大系数比D(rN)/D(0)即为考虑和不考虑人桥相互作用时的结构动力响应峰值之比。据此，考虑人桥相互作用时结构的动力响应峰值即可在不考虑人桥相互作用时的响应峰值基础上，结合动力放大系数进行估算。

4算例与估算方法正确性验证

4.1算例

为了说明上述方法的计算步骤并验证其正确性，现以某座混凝土人行桥为算例，分别通过估算方法和时程模拟方法计算了该人行桥在人桥相互作用下的峰值位移响应，并对结果进行对比。

混凝土人行桥的结构参数以及根据(20)式计算得到的临界人数如表3所示。

表3　算例的结构参数

4.2本文方法的计算步骤

根据本文提出的估算方法，结合以上算例，可将计算步骤总结如下(这里行人侧向步频取定值0.925 Hz)：

(1)按式(27)计算出频率比β=1.008，并按式(26)和式(30)计算当rN=0, 0.05, 0.1, 0.15,…, 0.7时的动力放大系数值，再计算动力放大系数比值D(rN)/D(0)；

(2)运用Monte Carlo模拟，以式(22)为计算模型，略去负阻尼项，计算不考虑人桥相互作用时的结构响应。模拟中随机生成行人侧向步行力，可以认为其各阶谐波相位服从[0,2π]间的均匀分布。动力响应采用时程分析法计算，取10~15 min间的计算结果作为结构稳态响应；

(3)按第(2)步重复进行1 500次模拟，取各次模拟响应峰值的均值，作为不考虑人桥相互作用的动力响应峰值；

(4)在上步结果的基础上乘以动力放大系数比D(rN)/D(0)，得到考虑人桥相互作用时的结构动力响应峰值。

4.3与时程分析的结果对比

将上述过程中(2)、(3)步的模拟结果进行拟合，可知不考虑人桥相互作用的结构动力响应峰值与(rN)0.5成正比关系(见图3，图4)，与Matsumoto[11]研究得到的人行桥竖向振动规律一致。

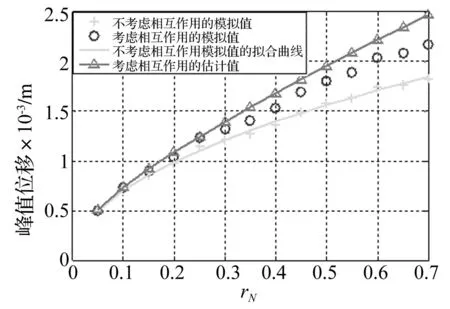
图3　结构峰值位移响应 Fig.3 Structural peak displacement

图4　结构峰值加速度响应 Fig.4 Structural peak acceleration

用同样的时程模拟方法，保留负阻尼项，并依次令rN=0.05, 0.1, 0.15,…, 0.7，可以得出考虑人桥相互作用的结构动力响应峰值。将该时程分析结果与上节计算过程得到的估算结果同时绘于图3，图4中。

由图3，4可知，当人数比在0.6以内，简化方法估算结果与时程分析结果的相对误差均在10%以内，当人数比为0.7时，结构峰值加速度响应的相对误差为12%。总体上估算结果略高于时程分析结果，两方法结果随rN变化趋势基本一致，说明上述估算方法正确反映了人桥相互作用对结构动力响应的影响规律。本文建议的估算方法计算步骤较为简单，相比于时程分析，所需的计算时间大大减少。

5结论

本文研究了人桥相互作用下结构的侧向振动，从行人在运动桥面上的行走步态规律出发，结合社会力模型提出了考虑人桥相互作用的侧向步行力表达式，并建立了负阻尼模型。由该模型推导了结构侧向振动的动力放大系数。在此基础上给出了运用动力放大系数估算结构动力响应的方法。该方法适用于低密度稳态人流行走激励下梁式结构的动力响应计算。最后，通过算例说明该方法估算值与时程分析结果基本一致，从而验证了该方法的有效性。

参考文献

[1]Dallard P, Fitzpatrick A J, Flint A, et al. The London Millennium Footbridge[J]. The Structural Engineer, 2001, 79(22): 17-33.

[2]Dallard P, Fitzpatrick A J, Flint A, et al. The Millennium Bridge, London: problems and solutions[J]. The Structural Engineer, 2001, 79 (8): 15-17.

[3]Fujino Y, Pacheco B M, Nakamura S I, at al. Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge[J]. Earthquake Eng. Struct. Dyn., 1993(22): 741-758.

[4]Nakamura S I, Kawasaki T. Lateral vibration of footbridges by synchronous walking[J]. Journal of Constructional Steel Research, 2006(62): 1148-1160.

[5]Roberts T M. Lateral pedestrain excitation of footbridges [J]. Journal of Bridge Engineering ASCE, 2005, 10(1): 107-112.

[6]Newland D E. Pedestrian excitation of bridges [J]. Mechanical Engineering Science, 2004, 218C: 477-492.

[7]Ricciardelli F, Pizzimenti A D. Lateral walling-induced forces on footbridges [J]. Journal of Bridge Engineering [J]. ASCE, 2008, 12(6): 677-688.

[8]Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic [J]. Nature, 2000(407): 487-489.

[9]宋志刚，金伟良. 行走激励下大跨度楼板振动的最大加速度响应谱法[J]. 建筑结构学报，2004(2)：57-63.

SONG Zhi-gang, JIN Wei-liang. Peak acceleration response spectrum of long span floor vibration by pedestrian excitation [J]. Journal of Building Structures, 2004(2): 57-63.

[10]Chopra A K. Dynamics of structures: theory and applications to earthquake engineering [M]. New York: Prentice-Hall, 2001.

[11]Matsumoto Y,Nishioka T, Shiojiri H. Dynamic design of footbridges[C]. International Association for Bridge and Structural Engineering, Proceedings, 1978: 17-28.

第一作者刘飞男，博士，讲师，1984年生

通信作者吴斌男，博士，教授，博士生导师，1962年生