基于附加源波叠加法的声辐射计算研究
2016-01-12夏雪宝,向阳
基于附加源波叠加法的声辐射计算研究
夏雪宝1,2,向阳1,2
(1.武汉理工大学能源与动力工程学院,武汉430063; 2.船舶动力系统运用技术交通行业重点实验室,武汉430063)
摘要:针对单极子波叠加法在特征波数处声场解的非唯一性问题,采用一种通过添加附加源克服解非唯一性的方法-附加源波叠加法,即在单极子波叠加法的基础上添加一定数量附加源从而获得声场全波数域内的唯一解。给出了具有解析解的脉动球源、振荡球源及无解析解的立方箱体结构三个数值算例。计算结果表明:对于脉动球源,添加一个附加源就可较好解决声场解的非唯一性问题;对于振荡球源,增加附加源个数可解决声场解的非唯一性问题,但会降低声场解的精度,但通过增加单极子源个数可以很好提高计算精度;该方法计算效率略低于复数矢径波叠加法,但较三极子波叠加法效率更高;对于立方箱体结构,确定了最佳的附加源个数,保证了声场解的唯一性。
关键词:波叠加法;非唯一性;附加源;声辐射
中图分类号:TB52文献标志码:A
基金项目:江苏高校优势学科建设工程资助项目;
收稿日期:2013-11-08修改稿收到日期:2014-01-15
基金项目:国家重点科技攻关项目(2011ZX06002-10-15,2011ZX06002-10-16);国家自然科学基金重大研究计划资助项目(91215301);北京市属高等学校创新团队建设提升计划资助
收稿日期:2013-08-15修改稿收到日期:2014-01-02
Acousticradiationcalculationbasedonadditionalsourceswavesuperpositionmethod
XIA Xue-bao1,2, XIANG Yang1,2(1.SchoolofEnergyandPowerEngineering,WUT,Wuhan430063,China; 2.KeyLaboratoryofMarinePowerEngineering&TechnologyMinistryofCommunication,Wuhan430063,China)
Abstract:The additional sources wave superposition method is a method of adding certain additional sources in monopole wave superposition method, which could overcome the problem of non-uniqueness of the acoustic field solution for fictitious wave numbers encountered in monopole wave superposition method. Three numerical examples about the sources of pulsating sphere, swing sphere and cube radiator were given. The numerical results demonstrate that the non-uniqueness problem can be removed by adding one source as for pulsating sphere source. The non-uniqueness problem also can be solved by adding more additional sources as for swing sphere source, but the computational accuracy will decline with the increase of the number of additional sources. By increasing the number of monopole sources, the additional sources wave superposition method can achieve high accuracy. The additional sources wave superposition method is somewhat less efficient than the wave superposition method with complex radius vector, but it is better than the tripole wave supposition method. As for the cube radiator, the acoustic uniqueness solution can be obtained by determining the optimized number of additional sources.
Keywords:wavesuperpositionmethod;non-uniqueness;additionalsources;acousticradiation
目前对于任意形状结构的声辐射及散射问题的研究主要是采用声边界元(BEM)的方法计算。由于边界元法能自动满足Sommerfeld边界条件及缩减求解问题的维度,因此较有限元法(FEM)效率更高。但边界方程在积分求解声辐射问题时会遇到积分的奇异性问题及在Dirichlet内问题的特征波数处解的非唯一性问题[1-3]。
不同于边界元法,Koopmann等[4]提出一种避免边界积分奇异性求解声场的方法-波叠加法(WSM)。该方法将一系列的等效声源(单极子源)置于辐射体内部,通过匹配辐射体表面速度边界条件求得单极子源的源强,再对单极子源的辐射声场进行叠加来求辐射体外部的声场解。由于单极子源是位于辐射体内部,避免了与辐射体边界表面重合,从而不存在积分的奇异性问题。单极子源的位置对声场求解的精度有很大影响[5],实际计算中往往将单极子源置于辐射体内部球面上或与辐射体形状相似的光滑曲面上。Jeans等[6]研究发现,由于单极子源所处位置为光滑封闭的曲面,会导致声场解在特征波数处出现非唯一性的问题,提出采用单极子源与偶极子源组合形式即三极子源(也称混合势)解决特征波数处解的非唯一性问题。向宇等[7]根据波叠加法与结构动力分析中的相似性,提出一种复数矢径波叠加法,该方法在单极子或偶极子波叠加法(也称单层势或双层势)的基础上,将单极子源所在曲面到中心点的矢径模值取为复数可以克服声场解在特征波数处的非唯一性问题。
用于求解辐射体声辐射和散射问题的基本解方法(MethodofFundamentalSolutions,MFS)可看成为一种间接边界元法[8]。该方法通过将点源置于辐射体内部(点源的初始位置为随机放置,在求解过程中可以进行优化至最佳位置),线性叠加一组基本解来获得声场的近似解,数值算例表明该方法可以避免声场解的非唯一性[9]。基于这一思路,本文采用一种新的克服在特征波数处解的非唯一性问题的波叠加法-附加源波叠加法。即在单极子波叠加法的基础上通过辐射体内部随机添加附加源的方法,该方法不仅成功克服解的非唯一性,而且三极子波叠加法更为节省计算时间。同时研究了附加源个数对计算结果的影响,增加附加源的个数可以有效克服解的非唯一性,但会造成计算整体精度的降低,通过增加单极子源的个数可以很好弥补该方法的不足,使精度达到计算要求。针对实际无解析解的立方箱体结构,采用附加源波叠加法计算时,确定了适宜的单极子个数及位置,并通过计算确定了最佳附加源个数。计算结果表明该方法能很好克服立方箱体结果声场解得非唯一性问题,并获得非常高的计算精度。
1波叠加法
通过叠加任意形状的辐射体内部光滑曲面上N个均匀分布等效声源的辐射声场,可得到辐射体外部区域的任一场点的声压解[10]如下所示
βnG(rm|rn)·nn]
(1)
式中:sn为等效声源强度;G(rm|rn)=eikR/R为自由空间格林函数[10];rn、rm分别为声源点及空间场点位置向量;R为声源点rn与空间场点rm之间的距离;i为虚数单位;k为波数;n为对声源点求梯度;nn为偶极子声源单位法向量。系数α和β的不同取值表示采用不同的等效声源的波叠加法。表1给出了α和β不同取值时对应的声源类型。

表1 不同 α和 β对应的声源类型
波叠加法是通过体积速度匹配来确定中的声源强度sn,进而求得声场解[10]。描述质点速度与声压关系的线性欧拉方程为v(rm)=p(rm)/ikρc,因此由式(1)可得到边界表面质点的法向速度为

βnG(rm|rn)·nn]·nm
(2)
式中:ρc为空气特性阻抗;nm为边界表面位置单位法向量;m为对边界表面质点求梯度。将边界表面离散为M个声学单元,则法向速度对单元面积的积分就可确定单元的体积速度为

βnG(rm|rn)·nn]·nmdSm
(3)
式中:Sm为表面单元m的面积区域。式(3)可用矩阵的形式表示为
u=Us
(4)
式中:u为表面单元体积速度向量,s为等效声源强度向量。矩阵U中的元素为

βnG(rm|rn)·nn]·nmdSm
(5)
通过体积速度边界条件根据式(4)求得声源强度,进而由式(1)可确定辐射声场的解。
2解的非唯一性及附加源波叠加法
Wilton等[11]指出,当应用单极子波叠加积分方程进行计算时,当计算的特征波数等于或接近单极子所在虚拟曲面上的边界条件为内部Dirichle条件所对应的特征波数时,方程的解会出现非唯一现象;采用偶极子波叠加方程计算时,当计算特征波数等于或接近虚拟曲面的边界条件为内部Neumann条件对应的特征波数时,方程的解也会出现非唯一现象;而采用三极子波叠加法时,特征波数不会等于或接近虚拟曲面的边界条件为内部Robin条件对应的特征波数,所以该方法可以保证解的唯一性。
基本解方法(MFS)是通过将一系列等效声源任意置于辐射体内部,通过叠加等效声源的辐射来求解辐射体的辐射声场解[9]。因此该方法也满足公式(1),与波叠加法具有相似性。两者的不同之处在于基本解方法是将等效声源任意置于辐射体内部,而波叠加法是将等效声源置于辐射体内部一光滑封闭曲面上。文献[9]指出基本解方法求解声辐射问题时能有效克服解的非唯一性,仅当等效声源位于特殊位置时才会存在解的非唯一性问题[12]。

图1 附加源波叠加法示意图 Fig.1 The additional sources wave superposition method
如图1所示,基于基本解方法的思想,在单极子波叠加法的基础上通过添加附加源(在辐射体内任意放置附加源,但要避开单极子源所在封闭曲面)来克服单极子波叠加法解的非唯一性问题,称该方法为附加源波叠加法。基于附加源波叠加法声场的解可表示为
(6)
式中,A为附加源的个数。附加源的作用是用来克服解的非唯一性,而整体的计算精度还是由单极子源的位置与个数决定。
3数值算例
为了确定附加源波叠加法是否能克服解的非唯一性问题及该方法求解的精度,采用具有解析解的脉动球源和振荡球源及无解析解的立方箱体对该方法进行数值验证。
3.1脉动球源
球心位于坐标原点的脉动球源的辐射声压解析解[13]为
(7)
式中:r为场点与脉动球源球心的距离;v为脉动球源表面振速幅值;a为脉动球源半径。规定半径a=1m,振速幅值v=1m/s。
单极子波叠加法计算时,单极子源均匀分布于半径b=0.5a球面上,单极子个数为91个。附加源波叠加法计算时,在单极子波叠加法的基础上,随机添加一个附加源(位于辐射体内部且避开单极子源所在球面),该源的坐标由Matlab随机生成(0.161 3m,0.550 1m,-0.677 6m)。用两种方法计算球面声压并与解析解对比如图2和3所示。


图2 脉动球源表面声压实部对比Fig.2Therealpartofthesurfacepressurecomparisionforpulsatingspheresource图3 脉动球源表面声压虚部对比Fig.3Theimaginarypartofthesurfacepressurecomparisionforpulsatingspheresource图4 声压解相对误差Fig.4Therelativeerrorofpressure
由图2和图3可以发现:采用单极子波叠加法求解,脉动球源在特征波数kb=π,2π,3π,…时,声压实部和虚部解出现非唯一现象;采用附加源波叠加法计算时,在整个波数域内声压解与解析解能很好吻合。
对比能够克服声场解的非唯一性问题的三种方法,附加源波叠加法、三极子波叠加法及复数矢量波叠加的计算时间及表面声压相对误差。声压相对误差定义为
(8)
式中:pa为波叠加法求计算得到的表面声压幅值;p为声压解析解幅值。三种方法等效声源个数(91个)及位置相同,附加源波叠加法多添加一个附加源。复数矢径波叠加法计算时,参照文献[7,13],单极子源所在球面复数半径取为b=(0.5+0.2i)a。三种方法计算结果如图4所示(k的步长为0.05)。
由图4可以发现,对于脉动球源,在分析波数内,三种方法都可以很好克服特征波数处解的非唯一性;三种方法中,附加源波叠加法计算精度最高,几乎为零,而采用三极子波叠加法误差保持4.5%以内,复数矢径波叠加法误差保持在1%以内;附加源波叠加法计算效率低于复数矢径波叠加法,但附加源波叠加法较三极子波叠加法高50%左右。由于附加源波叠加法较单极子波叠加法仅添加少量单极子源,而复数矢径波叠加法是将单极子所在曲面中心点的矢径模值取为复数,无需增加单极子源个数。因此三种方法中,复数矢径波叠加法效率最高,附加源波叠加法第二,而三极子波叠加法效率最低。
3.2振荡球源
坐标原点处沿x轴方向振荡球源的辐射声压解析解[13]为
(9)
式中:θ为场点与振荡方向x轴的夹角。同样规定球源半径a=1m,沿x轴方向振荡的速度幅值v=1m/s。单
极子波叠加法计算时,单极子源均匀分布于半径b=0.5a球面上,单极子个数为91个。附加源波叠加法计算时,在单极子波叠加法的基础上,随机添加一个附加源(位于辐射体内部且避开单极子源所在球面)。用两种方法计算θ=0处球面声压并与解析解对比如图5和6所示。
由图5和图6可知,波数kb=4.493 4,7.725 2,…时,采用单极子波叠加法及1个附加源的附加源波叠加法都存在声场解的非唯一性。这是由于附加源个数不够,不足以克服解的非唯一性。因此,在91个单极子源的基础上,对比分析附加源个数为3、5、7时声场的解,研究附加源个数对计算结果的影响规律,计算结果如图7和图8所示。


图5 振荡球源θ=0处表面声压实部对比Fig.5Therealpartofthesurfacepressurecomparisionforswingspheresource(θ=0)图6 振荡球源θ=0处表面声压实部对比Fig.6Theimaginarypartofthesurfacepressurecomparisionforswingspheresource(θ=0)图7 不同附加源个数振荡球源θ=0处表面声压实部对比Fig.7Therealpartofthesurfacepressurecomparisionofvariousadditionalsourcesforswingspheresource(θ=0)

图8 不同附加源个数振荡球源θ=0处表面声压虚部对比Fig.8Theimaginarypartofthesurfacepressurecomparisionofvariousadditionalsourcesforswingspheresource(θ=0)图9 不同单极子源个数振荡球源θ=0处表面声压实部对比(附加源个数为7个)Fig.9Therealpartofthesurfacepressurecomparisionofvariousmonopolesourcesforswingspheresource(θ=0,A=7)图10 不同单极子源个数振荡球源θ=0处表面声压虚部对比(附加源个数为7个)Fig.10Theimagnarypartofthesurfacepressurecomparisionofvariousmonopolesourcesforswingspheresource(θ=0,A=7)
由图7和图8可以得出:当附加源个数增加为3个时,声场的解在特征波数处任存在非唯一性问题;附加源个数为5个或7个时,保证了解的唯一性,但随附加源个数的增多,计算的整体精度有所降低。由文献[5]可知,波叠加法中等效源的数量与位置决定计算精度,因此采用附加源波叠加法造成计算精度的降低可以通过改变单极子数目和位置来弥补。在不改变单极子源所在封闭球面半径的情况下,对比分析不同数量单极子个数对附加源波叠加法的影响。单极子源个数分别为91、153、250(附加源个数为7)时,振荡球源表面声压解(θ=0)如图9和图10所示,相应的误差对比如图11所示。

图11 不同单极子源个数振荡球源θ=0处 表面声压误差对比(附加源个数为7个) Fig.11 The relative error of pressure comparision of various monopole sources for swing sphere source (θ=0, A=7)
由以上声压及误差对比可以发现,附加源个数不变的情况下,增加单极子源的个数为153个时,声压最大误差由91个单极子源的20%左右下降到5%以内。而当单极子源个数为250个时,误差可以忽略不计,声压解具有相当高的精度(对于θ=30、45、60、90,求得的表面声压解也满足计算精度要求)。因此,采用附加源波叠加法克服解的非唯一性而造成计算整体精度的降低,可以通过增加单极子源的个数来解决,使计算结果即克服了解的非唯一性又具有相当高的精度。
对于振荡球源,在250个单极子源情况下,添加7个附加源就可以很好克服声场解的非唯一性问题,同时可以保证非常高的整体计算精度。为进一步验证该方法的计算效率及精度,对比附加源波叠加法、三极子波叠加法及复数矢径波叠加法的计算效率及精度。三种计算方法的等效声源个数均为250个且位置相同,附加源波叠加法多添加7个附加源。采用复数矢径波叠加法计算时,单极子源所在复数失径取为b=(0.5+0.2i)a。三种方法计算振荡球源θ=0处表面声压误差及计算时间对比结果如图12所示(k的步长为0.05)。
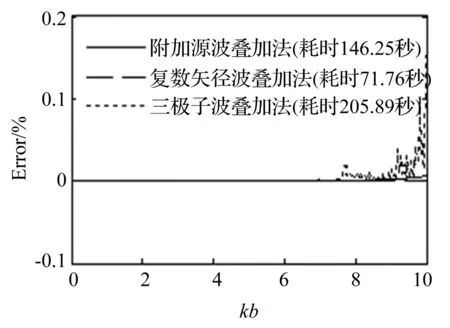
图12 声压解相对误差 Fig.12 The relative error of pressure
由图12 可以发现,对于振荡球源,在分析波数内,三种方法都可以克服特征波数处解的非唯一性;三种方法计算误差均在0.2%范围以内,几乎可以忽略不计,具有非常高的精度;与脉动球源一样,附加源波叠加法计算效率低于复数矢径波叠加法,但高于三极子波叠加法。
3.3立方箱体结构
对于实际复杂结构采用附加源波叠加法进行声场计算时会遇到如何确定单极子源个数、单极子源位置、附加源个数及附加源位置这些问题。对于实际结构,一般是将辐射体表面离散成声学单元,将表面单元中心点坐标乘以缩放系数获得单极子源所在位置坐标。因此对于单极子源个数的确定问题,因单极子个数与辐射体表面个数相等,可借鉴边界元法,即保证表面单元满足表面单元尺寸小于λ/6(λ为声波波长)[14],进而初步确定单极子源个数,若计算后整体精度不满足要求,则可增加单极子源个数来提高计算精度。对于如何确定单极子源位置的问题,由于单极子源位置一般是通过边界表面单元中心点进行同形缩放获得,同形缩放系数范围为0到1,且缩放系数不能太大或太小。因为缩放系数太大时,单极子源距边界表面过近,计算时格林积分会出现近奇异性,计算误差较大;缩放系数太小时,单极子源所在曲面变小,单极子源之间的距离过近,会导致矩阵变换时向量组高度线性相关,计算结果不精确。因此可通过计算选取合适同形缩放系数,进而获得单极子源所在位置。对于附加源位置确定的问题,附加源位置为程序随机生成但要保证避免位于单极子源所在曲面。而附加个数则需通过分析计算结果,确定能保证声场唯一解的最佳附加源个数。

图13 立方箱体边界元模型 Fig.13 The boundary element model of the cube
为进一步验证附加源波叠加法对无解析解实际结构声场计算的有效性,以边长为1m的立方箱体为对象进行计算验证。该立方箱体的边界元网格模型如图13所示,总共150个表面单元。计算时,取每个表面单元中心点坐标乘以缩放系数进行同形缩放来获得单极子源所在位置坐标。
对于模拟实际结构的立方箱体,声辐射并无解析解可循,因此在立方箱体中心处放置一个声源强度s=ikρc的简单源(单极子源)。以该简单源在箱体表面单元中心点产生的质点速度作为该箱体的速度边界条件,简单源在单元中心点处的辐射声压则作为标准声压。由于立方箱体表面不同单元中心点声压不相等,因此表面声压相对误差定义为
(10)
式中,pa,i为波叠加法求得表面单元中心点处声压幅值,pi为立方箱体中心处简单源辐射到表面单元i中心点处声压幅值,i=1…N,N为表面单元个数。采用单极子波叠加法求解立方箱体结构辐射声场,无法事先获知该结构对应的特征波数,因此采用单极子波叠加法求解辐射箱体表面声压相对误差,分析该结构对应的特征波数,计算结果如图14所示(计算时缩放系数取为0.75)。

图14 表面声压相对误差 Fig.14 The relative error of pressure
由图14可以发现,采用单极子波叠加法计算时分析波数范围内立方箱体表面声压解存在3个特征波数点分别为k=7.2、13.85、18.1;计算波数接近或等于特征波数时表面声压相对误差增大,其它波数处单极子波叠加法计算精度非常高,因此也说明取的单极子源个数及缩放系数非常合理。为克服单极子波叠加法声场解在特征波数处非唯一性问题。在单极子波叠加法的基础上,添加A=7个附加源计算表面声压相对误差并与单极子波叠加法进行对比,结果如图15所示(经计算A=7时,计算结果最好)。附加源位置由Matlab随机生成,但避免与单极子源所在立方体重合。

图15 表面声压相对误差 Fig.15 The relative error of pressure
由图15可以发现,对于模拟实际结构的立方箱体,采用附加源波叠加法进行声场计算,添加7个附加源就能很好克服单极子波叠加法在特征波数处声场解的非唯一性问题,并保证了非常高的整体计算精度。因此,附加源波叠加方法对于模拟实际结构的立方箱体也一种有效、可行的声场计算方法。
4结论
在单极子波叠加法的基础上,通过在辐射体内部添加一定数量的附加源克服了单极子波叠加法在特征波数处解的非唯一性问题。数值算例表明,该方法计算效率及精度优于三极子波叠加法;对于模拟实际结构的立方箱体,该方法也能很好克服声场解的非唯一性问题并能保证非常高的计算精度。如何优化附加源及单极子源的数目和位置,使计算精度和效率同时达到最高还有待今后进一步深入研究。
参考文献
[1]胡海昌. 论Helmholtz方程的一类边界积分方程的合理性[J].振动工程学报,1992, 5(3): 183-192.
HUHai-chang.OntherationalityofaclassofboundaryintegralequationsforHelmholtzequation[J].JournalofVibrationEngineering, 1992, 5(3): 183-192.
[2]BenthienW,SchenckA.Nonexistenceandnonuniquenessproblemsassociatedwithintegralequationmethodsinacoustics[J].Computers&Structures, 1997, 65(3): 295-305.
[3]王清, 徐博侯. 关于Helmholtz外问题的边界积分方程解的唯一性问题[J]. 应用数学与力学, 1990, 11(10): 903-909.
WANGQing,XUBo-hou.OntheuniquenessofboundaryintegralequationfortheexteriorHelmholtzproblem[J].AppliedMathematicsandMechanics, 1990, 11(10): 903-909.
[4]KoopmannGH,SongL,FahnlineJB.Amethodforcomputingacousticfieldsbasedontheprincipleofwavesuperposition[J].J.Acoust.Soc.Am, 1989, 86(6): 2433-2438.
[5]SongL,KoopmannGH,FahnlineJB.Numericalerrorsassociatedwiththemethodofsuperpositionforcomputingacousticfields[J].J.Acoust.Soc.Am, 1991, 89(6): 2625-2633.
[6]JeansR,MathewsIC.Thewavesuperpositionmethodasarobusttechniqueforcomputingacousticfields[J].J.Acoust.Soc.Am, 1992, 92(2): 1156-1166.
[7]向宇, 黄玉盈. 基于复数矢径的波叠加法解声辐射问题[J]. 固体力学学报, 2004, 25(1): 35-40.
XIANGYu,HUANGYu-ying.Wavesuperpositionmethodbasedonvirtualsourceboundarywithcomplexradiusvectorforsolvingacousticradiationproblems[J].ActaMechanicsolidasinica, 2004, 25(1): 35-40.
[8]FairweatherG,KarageorghisA,MartinPA.Themethodoffundamentalsolutionsforscatteringandradiationproblems[J].EngineeringAnalysiswithBoundaryElements, 2003, 27: 759-769.
[9]KondapalliPS,ShippyDJ.Analysisofacousticscatteringinfluidsandsolidsbythemethodoffundamentalsolutions[J].J.Acoust.Soc.Am, 1992, 91(4): 1844-1854.
[10]KoopmannGH.Designingquietstructures[M].SanDiego:Acadmic, 1997.
[11]WiltonDT,MathewsIC,JeansRA.Aclarificationofnonexistenceproblemswiththesuperpositionmethod[J].J.Acoust.Soc.Am, 1993, 94(3): 1676-1680.
[12]ChenIL.Usingthemethodoffundamentalsolutionsinconjunctionwiththedegeneratekernelincylindricalacousticproblems[J].JournaloftheChineseInstituteofEngineers, 2006, 29(3): 445-457.
[13]高煜. 基于波叠加方法的声辐射与声学灵敏度算法的若干关键问题研究[D]. 合肥:合肥工业大学, 2009, 9.
[14]吴绍维, 向阳, 夏雪宝. 基于无单元声波叠加的自辐射近似解析表达研究[J]. 振动与冲击, 2014, 33(7): 79-85.
WUShao-wei,XIANGYang,XIAXue-bao.Approximateanalyticalexpressionsofself-radiationtermsincladingacousticpressureandvelocitybasedonelementfreeacousticwavesuperposition[J].JournalofVibrationandShock, 2014, 33(7): 79-85.

第一作者石海忱男,硕士生,1989年8月生
通信作者陈前男,教授,博士生导师,1951年生

第一作者李小军男,研究员,博士生导师,1965年生
通信作者侯春林女,博士,高级工程师,1981年生
邮箱:hou.chunlin@gmail.com
