EASE-Grid投影对青藏高原雪水当量产品的验证影响分析

2016-01-11宾婵佳,邱玉宝,牛静静等

遥感信息 2015年1期

宾婵佳1，邱玉宝1，牛静静1，郑照军2

(1.中国科学院遥感与数字地球研究所数字地球重点实验室，北京 100094；2.国家卫星气象中心卫星气象研究所，北京 100081)

摘要：本文介绍EASE-Grid 3种投影的定义，利用地面实测数据和理论方式开展不同投影下AMSR-E 雪水当量(SWE)产品的精度验证对比分析，研究其不同投影导致误差产生的原因。验证对比结果表明，青藏高原地区北半球方位角等积投影和全球圆柱体等积投影对于验证结果具有很大影响。理论分析结果表明，我国青藏高原地区在全球圆柱体等积投影下网格发生的形变较小，更适合采用全球圆柱体等积投影。进一步研究表明，AMSR-E亮温数据轨道采样点落入北半球方位角等积投影和全球圆柱体等积投影对应网格差异较大。雪水当量产品验证结果的误差包含了算法误差和投影带来的误差。在开展大尺度遥感反演时，应根据具体研究区所处的纬度范围及研究目的，选取适合的投影方式以降低投影引起的误差。

关键词：EASE-Grid投影；青藏高原；验证误差分析；积雪遥感

doi:10.3969/j.issn.1000-3177.2015.01.016

中图分类号：TP79文献标识码：A

收稿日期：2013-10-23修订日期：2013-11-27

作者简介：张增(1986～)，男，硕士，工程师，研究方向为模拟识别、目标跟踪、电子稳像。

收稿日期：2014-03-28修订日期：2014-05-04

作者简介：杨会元(1988～)，男，硕士研究生，主要研究方向为遥感图像检索。

通讯作者：冯钟葵(1960～)，男，研究员，主要研究方向为遥感数据处理、图像处理、海量数据存储与管理与遥感地面系统集成。

Validation Impact Analysis of Snow Water Equivalent Product Using

EASE-Grids Projection over Tibetan Plateau

BIN Chan-jia1，QIU Yu-bao1，NIU Jing-jing1，ZHENG Zhao-jun2

(1.KeyLaboratoryofDigitalEarthScience，InstituteofRemoteSensingandDigitalEarth，

ChineseAcademyofSciences，Beijing100094；

2.NationalSatelliteMeteorologicalCentre，Beijing100081)

Abstract：In this paper，three EASE-Grids projection were described，in situ snow depth data and theoretical analysis were used to validate AMSR-E SWE product on different projects，and then the causes of error was analyzed.Verification results showed that validation results under northern hemisphere azimuth equal-area projection and global cylinder equal-area projection over the Tibetan plateau have a great influence.Theoretical analysis results showed that grid deformation is small over the Tibetan plateau in China under the global cylinder equal-area projection，and it is more suitable for global cylinder equal-area projection in this area.Further research shows that difference of AMSR-E bright temperature data samplings dropping into the northern hemisphere equal-area projection and global cylinder equal-area projection corresponding grids are very large.Validation error of SWE product contains algorithm error and projection error.When carrying out large scale remote sensing inversion，in order to reduce the error caused by projection，appropriate projection should be chosen in specific research area and for specific research purposes.

Key words：EASE-Grid projection；Tibetan plateau；validation error analysis；snow remote sensing

1引言

目前，世界上定义的地图投影种类繁多，各投影所针对的研究区范围、科学范畴都不尽相同。地图投影可将不同来源的空间数据通过空间定位框架定位于公共的地理基础之上，地球观测产品必须基于地图投影呈现其可视化结果。EASE-Grid投影是由美国冰雪数据中心(NSIDC)发展的一种等面积投影，其全称为等面积可扩展地球网格，是一种全球尺度网格化数据的通用格式，特别适用于大尺度遥感数据。雪水当量是重要的积雪参数之一，它影响着地球水文圈和冰冻圈的运动，对区域乃至全球的气候变化都有着深刻影响。随着多通道微波辐射计(SMMR)、专用微波成像辐射计(SSM/I)和高级微波扫描辐射计(AMSR-E)相继投入使用，生成了自1978年至今的积雪数据集，积雪数据集多数采用EASE-Grid投影方式，其投影网格随着纬度的变化会发生一定的形变。目前的EASE-Grid投影包括3种：南、北半球的方位角等积投影与全球的圆柱等积投影。这三种投影都是基于地球球状模型，采用的地球半径为6371.228km。选择EASE-Grid投影，能大大简化数据的可视化和相互操作，使分析和对比更方便。但是，我国属于中低纬度国家，地面站点观测的常年有积雪覆盖的地区纬度范围为30°N～53°N，EASE-Grid投影在中低纬度地区的适用性还需要做进一步的分析研究。

因此，为了明确青藏高原地区EASE-Grid投影对于积雪产品精度的影响，本文将首先介绍EASE-Grid的3种投影定义，利用地面实测数据对比验证北半球方位角等积投影和全球圆柱体等积投影下积雪产品的精度，并从以下两方面分析产生误差的原因：两种投影随着纬度变化而发生的形变比和AMSR-E亮温数据轨道采样点与投影网格的空间关系。

2EASE-Grids简介[1]

EASE-Grid是基于美国雪冰数据中心发展的数字地图和网格定义的理论发展而来的一种网格定义，这种理论建立了一个软件程序库，假设网格数据集完全被定义为地图投影和网格点的覆盖晶格。EASE-Grid包含有3种投影，并有无限种可能的网格定义，以便于扩展应用。因此，EASE-Grid是一个通用工具，便于用户处理全球尺度的网格数据。EASE-Grid目前有两个版本，第一个版本于1992年定义，被广泛应用于许多数据集，EASE-Grid 2.0定义于2011年，被一些新的数据集所采用。1992年版EASE-Grid包含的3种投影分别为：南半球方位角等面积投影、北半球方位角等面积投影和全球圆柱等积投影。

北半球方位角等积投影定义：

r=2×R/C×sin(lambda)×sin(PI/4-phi/2)+r0

(1)

s=2×R/C×cos(lambda)×sin(PI/4-phi/2)+s0

(2)

h=cos(PI/4-phi/2)

(3)

k=sec(PI/4-phi/2)

(4)

南半球的方位角等积投影定义：

r=2×R/C×sin(lambda)×cos(PI/4-phi/2)+r0

(5)

s=-2×R/C×cos(lambda)×cos(PI/4-phi/2)+s0

(6)

h=sin(PI/4-phi/2)

(7)

k=csc(PI/4-phi/2)

(8)

全球圆柱等积投影定义：

r=r0+R/C×lambda×cos(30)

(9)

s=s0-R/C×sin(phi)/cos(30)

(10)

h=cos(phi)/cos(30)

(11)

k=cos(30)/cos(phi)

(12)

其中，r为列号；s为行号；h为沿经线方向的比例；k为沿纬线方向的比例；lambda为经度弧度；phi为纬度弧度；R为地球半径(6371.228km)；C为像元大小(25km)；r0为地图原点的列号；s0为地图原点的行号。

3EASE-Grids投影下青藏高原地区AMSR-E SWE精度对比验证

本节将以青藏高原地区为研究区，基于AMSR-E SWE算法[2-4]，将估算结果分别投影为北半球方位角等积投影和全球圆柱体等积投影。利用地面实测数据，对比验证两种投影结果的SWE精度，从而了解投影对于算法精度的影响。

对比验证工作采用的卫星数据为2009年11月15日～16日AMSR-E L2A Swath降轨亮温数据，选取降轨数据是因为卫星经过我国境内的时间区间为UTC 15时～22时之间，换算成北京时间为当天23时～次日06时，此时是一天中温度较低的时间段，积雪基本处于干雪未融化状态。采用的验证数据为对应时段的地面实测数据。地面数据记录的观测内容有观测点经纬度及雪深(cm)。

雪深算法的评价指标有相关系数(R)、均方根误差(RMSE)。R的大小决定实测值与模拟值相关的密切程度。R越接近1，表示相关的雪深算法参考价值越高；相反，越接近0，表示参考价值越低。RMSE是用来衡量估算雪深与实测雪深值之间的偏差，说明样本的离散程度。

地面观测数据对比步骤：①在利用地面数据对比之前，要对地面数据进行预处理，即采用积雪密度值0.239235g/cm3，将地面观测的雪深(cm)数据转换成观测的雪水当量(mm)数据。②利用地面观测点的经纬度，分别转换成EASE-Grid北半球方位角等积投影和全球圆柱体等积投影下对应的网格行列号，并提取两种网格中的SWE值。即得到两种投影下32个地面观测的SWE值的对比结果(表1)。从结果中可以看到，超过一半对应网格的结果存在差异，部分网格中的地面观测SWE值相差较大。

SWE算法精度验证步骤：①利用AMSR-E L2A Swath降轨亮温数据，根据AMSR-E SWE算法的处理步骤，先在轨道亮温数据上计算每个像元的雪水当量值，再将估算的SWE值投影到北半球方位角等积投影和全球圆柱体等积投影。②将两种投影下估算的SWE结果与地面实测SWE数据对比，计算青藏高原地区EASE-Grids投影下算法反演结果的R和RMSE，验证两种投影结果的精度(表2)。

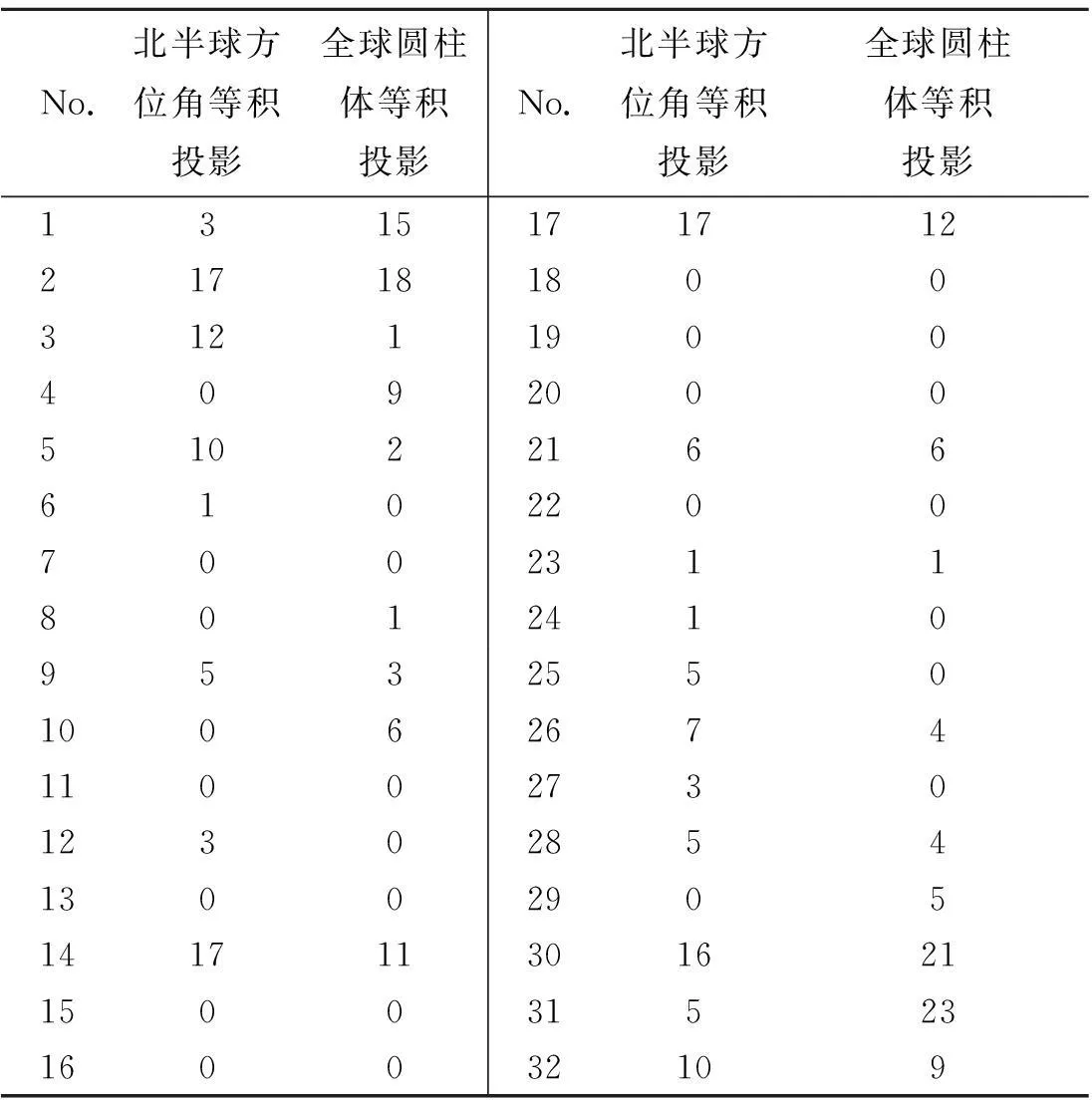
表1　EASE-Grids网格雪水当量(SWE)对比/mm

统计分析得到所有结果如表2所示，该区在北半球方位角等积投影下的算法的R为0.46，RMSE为8.48mm，优于全球圆柱体等积投影的0.24和9.81mm。

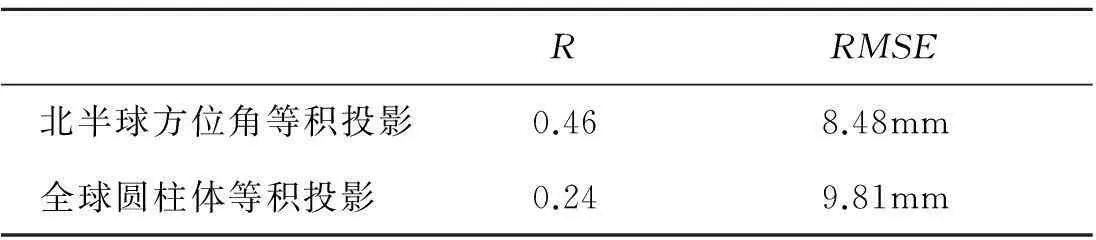
表2　EASE-Grids投影下雪水当量(SWE)算法精度统计表

通过表2的结果可以看到，在所用数据相同、雪水当量算法相同的情况下，选择不同投影对最终的算法精度会产生不同程度的影响。针对这一现象，文章将从两方面分析产生误差的原因，即两种投影随着纬度变化而发生的形变比，AMSR-E亮温数据轨道采样点与投影网格的空间关系。

4误差结果分析

4.1EASE-Grids投影网格形变研究

地图投影的两个最终的特征是：等角和等面积，没有一种地图投影是二者兼而得之的[5]。采用等面积投影的产品都会发生一定的形变，沿着经度线的比例h与沿着纬度线的比例k，纵横比k∶h则称为变形。因此，对于形状变形还是面积变形或者是形状和面积都发生变形这三种情况，在EASE-Grids中选择等面积投影，是因为该投影在半球和全球尺度上能最小化变形的数量。使用等面积投影的另一个重要原因是，在统计面积时，只需要知道网格总数及1个网格所代表的面积，就能快速方便地求出总面积，这也正体现了EASE的含义，即便于使用。

表3为北半球范围上EASE-Grid两种投影的纵横比对比表。从表中可以看出，对于方位角等积投影，其纵横比例从两极的1∶1变化到赤道的2∶1，形变变化范围较小。对于全球的圆柱体等积投影，其形变比变化范围为24.90～0.75，形变在北纬80°达到最大(即24.90)，在赤道地区则变为0.75。值得注意的是，全球的圆柱体等积投影在北纬30°的形变比为1，这是由于该投影选取南北纬30°作为圆柱投影的标准纬线，确保在陆路范围有最小的平均角度变形。因此，全球的圆柱体等积投影适用于在中-低纬度地区的研究[2]。

青藏高原地区的纬度范围约为25.74°N～40.20°N，属于中低纬度地区，表4为青藏高原地区纬度范围EASE-Grid两种投影的形变比。结果显示，在25.74°N～38°N范围内，全球圆柱体等积投影网格发生的形变较小，投影网格基本可认为是正方形。在39°N～40.20°N范围内，北半球方位角等积投影的形变比小于全球圆柱体等积投影。总体而言，基于全球圆柱体等积投影，青藏高原大部分区域的纵横比都接近1∶1，在该投影方式的下的形变相对较小。

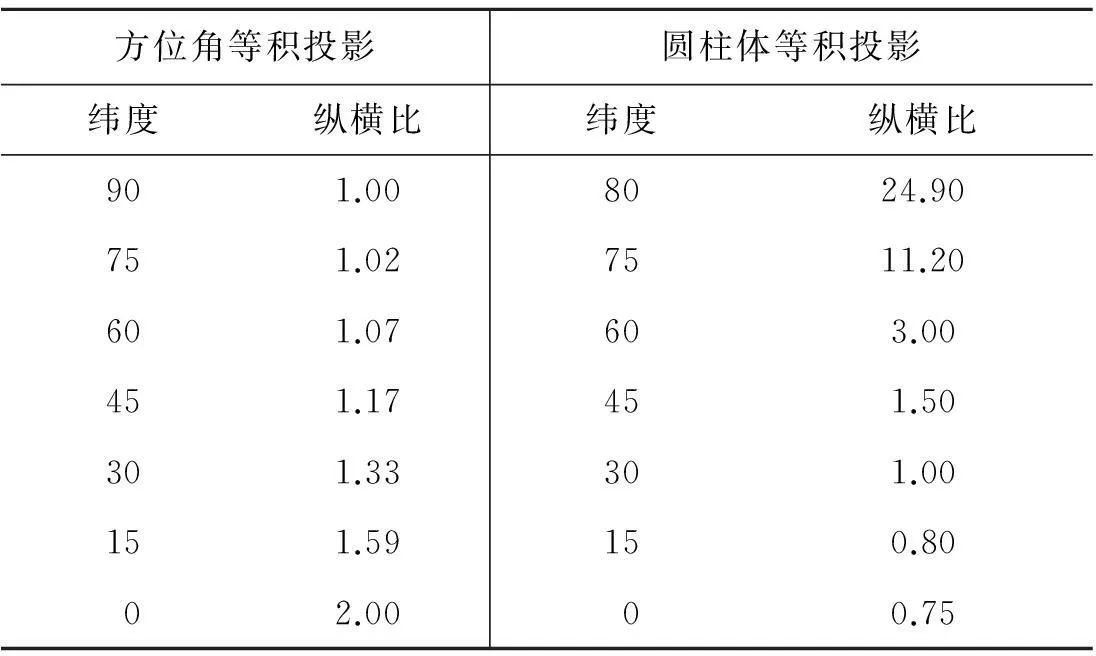
表3　北半球EASE-Grid投影形变比 [1]

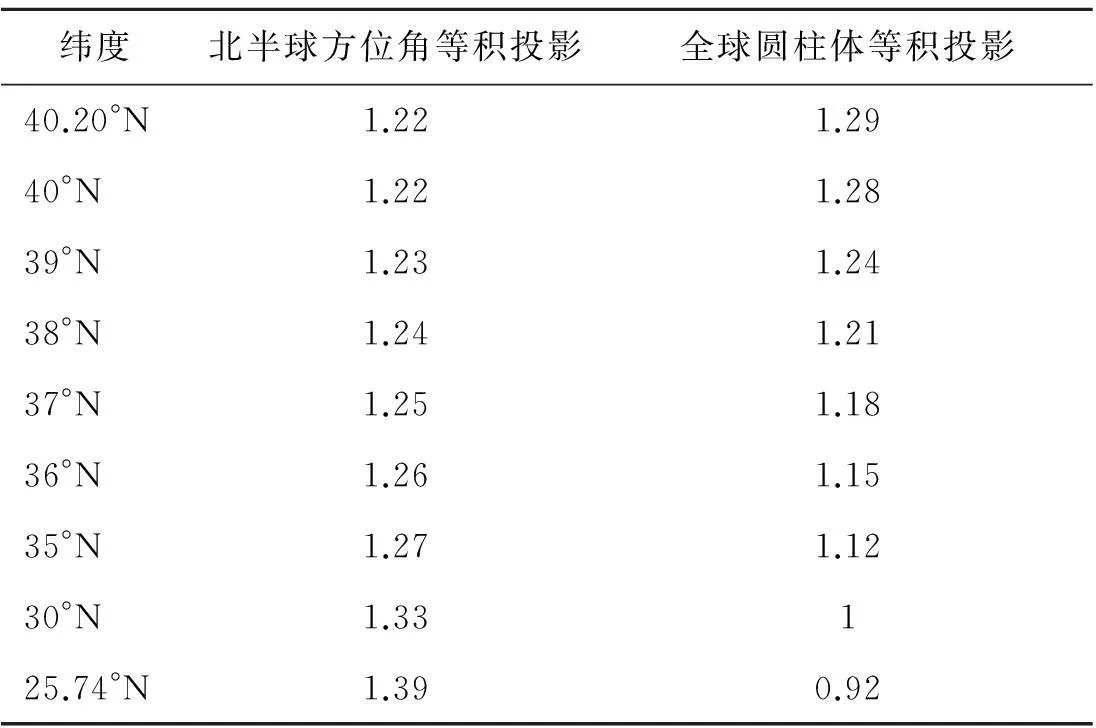
表4　青藏高原EASE-Grid投影形变比

为了更直观地了解北半球地区EASE-Grid两种投影随着纬度变化而发生的形变情况，文章将利用北半球方位角等积投影的转换公式，得到北半球范围内的方位角等积投影网格顶点的经纬度；利用全球圆柱体等积投影转换公式，得到北半球地区圆柱体等积投影的网格顶点经纬度。再将两种投影网格顶点的经纬度投影到地球上(图1)，可以直观地比较两种投影网格的形状及所代表的区域。图1是在7个纬度点附近，即0°N、15°N、30°N、45°N、60°N、75°N、90°N附近的投影网格覆盖情况。在赤道附近，北半球方位角等积投影投影网格呈拉长型的平行四边形，而全球圆柱体等积投影网格则是长宽相差不大的矩形。到了北纬30°附近，方位角等积投影投影网格仍然为平行四边形，圆柱体等积投影网格近似于正方形。随着纬度的不断升高，在北极地区，方位角等积投影投影网格变成很规则的正方形，圆柱体等积投影网格则逐渐拉长，形成一个长宽比相差很大的矩形。这个投影结果也正好印证了表1中两种投影的纵横比变化的情况。

图1　EASE-Grids投影网格图 (图中为等经纬度间距；红色圆点为方位角等积投影网格顶点；蓝色方点为圆柱体等积投影网格顶点)

4.2EASE-Grids投影网格采样点研究

进行投影时，轨道数据分别落入的两种投影网格内的采样点数量不相同，存在大量非重叠的采样点，从而造成最终投影网格内的数值的变化差异。从轨道数据采样点转变成EASE-Grids投影网格的过程如图2所示。

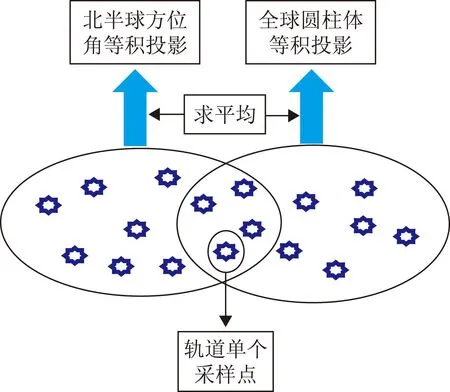
图2　投影网格采样点分配示意图

图3则是利用AMSR-E L2A亮温数据[6]，将东经100°上的0°N、15°N、30°N、35°N、45°N、50°N、60°N、75°N和85°N分别转换成北半球方位角等积投影和全球圆柱体等积投影下所对应的行列号，记录并提取落入这两种投影下对应网格的采样点经纬度，在ArcGIS中将落入两种投影的网格中采样点投到全球地图上。通过图3可以看出，由于纬度的不同，两种投影重叠的区域中采样点也不同。其中，在0°N、35°N、45°N和75°N的重叠区的采样点很少。大部分的结果中，两种投影在相同的纬度转换得到的行列号中所包含采样点不同，其所代表的地物不同，代表性差异较大，导致两种投影的可比较性较差。

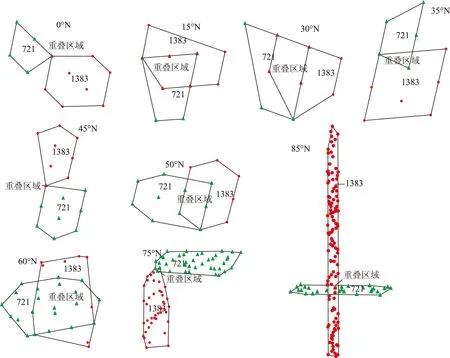
图3　AMSR-E L2A轨道亮温数据EASE-Grids投影图

5结束语

本文介绍了EASE-Grid 3种投影的定义，利用地面实测数据对比验证了北半球方位角等积投影和全球圆柱体等积投影下积雪产品的精度，并从两方面分析产生误差的原因。总结得到四点结论：

(1)在青藏高原地区对比验证两种投影下AMSR-E SWE算法的精度，表明不同投影对于验证结果具有较大影响。

(2)EASE-Grid理论结果表明，全球圆柱体等积投影适用于中低纬度地区，投影网格在青藏高原地区网格形变较小，青藏高原地区更适合采用全球圆柱体等积投影。

(3)分析AMSR-E亮温数据轨道采样点与投影网格的空间关系，采样点落入北半球方位角等积投影和全球圆柱体等积投影对应网格的数量差异较大。

(4)地面实测数据的空间位置对于验证具有较大影响。由于地面数据获取难度较大，往往在1个EASE-Grid投影网格内只有1个实测数据，该采样点在空间上具有随机性，表1中超过一半对应网格的地面实测数据结果存在差异，部分网格中的地面观测SWE值相差较大。因此，即使青藏高原地区更适合采用全球圆柱体等积投影，由于投影对实测数据空间位置的影响，仍然出现全球圆柱体等积投影下精度略低于北半球方位角等积投影的验证结果。

在青藏高原地区验证积雪产品的精度时，验证的误差除了包含算法本身的误差外，还会受到所用投影带来的误差。因此，在开展大尺度遥感反演时，应根据具体研究区所处的纬度范围及研究目的，选取适合的投影方式以降低投影引起的误差。

参考文献：

[1]BRODZIK M J，KNOWLES K W.EASE-Grid：A versatile set of equal-area projections and grids[EB/OL].Discrete Global Grids，National Center for Geographic Information and Analysis，Santa Barbara，CA，USA：National Center for Geographic Information & Analysis，http：//www.ncgia.ucsb.edu/globalgrids-book/ease_grid/2002.

[2]CHANG A T C，FOSTER J，HALL D K.NIMBUS-7 SMMR derived global snow cover parameters[J].Annals of Glaciology，1987，(9)：39-44.

[3]KELLY R E J，CHANG A T C，TSANG L，et al.A prototype AMSR-E global snow area and snow depth algorithm[J].IEEE Transactions on Geoscience and Remote Sensing，2003，41(2)：230-242.

[4]KELLY R.The AMSR-E snow depth algorithm：Description and initial results[J].Journal of the Remote Sensing Society of Japan，2009，(29)：307-317.

[5]KNOWLES，KENNETH W.Points，pixels，grids，and cells—a mapping and gridding primer[J].Unpublished Report to the National Snow and Ice Data Center，Boulder，Colorado USA，1993.

[6]ASHCROFT P，FRANK W.AMSR-E/Aqua LZA gLOBAL swath spatially-resampled brightness tem peratures Vooz，[EB/OL].http：//nsidc.org/data/docs/daac/ae_l2a_tbs.gd.html，2009-11-15.