应用MODIS地表温度产品估计新疆典型区气温

应用MODIS地表温度产品估计新疆典型区气温

袁敏1，2，3，肖鹏峰1，2，3，冯学智1，2，3，朱榴骏1，2，3

(1.江苏省地理信息技术重点实验室，南京 210023；2.卫星测绘技术与应用国家测绘地理信息局重点实验室，南京 210023；3.南京大学 地理信息科学系，南京 210023)

摘要：根据遥感获取的地表温度估计气温在时空上的连续分布有重要意义。利用MODIS传感器反演的地表温度产品分别建立新疆克拉玛依气象站生长季节、非生长季节的地表温度和气温的线性回归模型以估计气温，并利用相同气象站不同时段、相同时段不同气象站的数据对该模型进行验证，最后得到新疆典型区内非生长季节的日最低、最高气温分布。结果表明：相对于MYD11A1产品，MOD11A1产品的地表温度数据能更好地估计气温；气温估计模型在生长季节效果欠佳，但在非生长季节结果较好，MOD11A1产品估计日最低气温的均方根误差和平均绝对误差分别为2.4℃～3.2℃、1.9℃～2.8℃，估计日最高气温的均方根误差和平均绝对误差分别为2.9℃～3.1℃、2.2℃～2.6℃，R2为0.91～0.96。

关键词：地表温度；气温；新疆；线性回归；生长季节；非生长季节

doi:10.3969/j.issn.1000-3177.2015.01.014

中图分类号：TP79文献标识码：A

收稿日期：2013-12-18修订日期：2014-03-03

基金项目：国家自然科学基金资助项目(41376178)；上海高校特聘教授(东方学者)岗位计划、上海市科学技术委员会的资助(11510501300)。

作者简介：刘风玲(1988～)，女，硕士，研究方向为GNSS-R在海面高度的研究与应用。

Air Temperature Estimation of Typical Area in Xinjiang Based on

MODIS Land Surface Temperature Products

YUAN Min1，2，3，XIAO Peng-feng1，2，3，FENG Xue-zhi1，2，3，ZHU Liu-jun1，2，3

(1.JiangsuProvincialKeyLaboratoryofGeographicInformationScienceandTechnology，NanjingUniversity，Nanjing210023；

2.KeyLaboratoryforSatelliteMappingTechnologyandApplicationsofStateAdministrationofSurveying，

MappingandGeoinformationofChina，NanjingUniversity，Nanjing210023；

3.DepartmentofGeographicInformationScience，NanjingUniversity，Nanjing210023)

Abstract：Accurate estimation of spatially distributed air temperature based on continuous land surface temperature (LST) products retrieved from remotely sensed images is of great significance.To estimate daily minimum and maximum air temperature，linear regression models of the growing and non-growing season on Karamay meteorological station were conducted respectively.Then two validation experiments were carried out，one of which took data collected from the same station in different periods to validate the models，while the other experiment applied the models to other stations.Finally，the validated models were used to produce full image coverage for the typical area of Xinjiang.The results showed that deprived LST from Terra platform (MOD11A1) had higher accuracy than deprived LST from Aqua platform (MYD11A1).Models of the non-growing season with R2=0.91～0.96 were better than those of the growing season.Moreover，this method provided an acceptable estimation of daily minimum air temperature with RMSE(root mean square error)=2.4℃～3.2℃ and MAE(mean absolute error)=1.9℃～2.8℃，and also improved the accuracy of daily maximum air temperature significantly with RMSE=2.9℃～3.1℃ and MAE=2.2℃～2.6℃ during the non-growing season.

Key words：land surface temperature；air temperature；Xinjiang；linear regression；growing season；non-growing season

1引言

气温(air temperature，Ta)是地面气象观测规定高度(国内为1.5m)上的空气温度[1]。气温调节了很多近地表过程，如植物的光合作用、呼吸作用、蒸腾作用等[2]，同时气温变化也影响着高山积雪与冻土、森林火灾监测和全球变暖等诸多方面，是各种植物、水文、气象、环境等模型中的一个重要近地表气象参数[3]。目前气温数据主要来自气象站点的观测，然而，气象站点只能提供空间上离散的有限点观测数据，作为区域气温的粗略代表。很多研究需要连续的气温面数据而非点数据，因此对气温在时空上连续分布的研究有重要意义。

传统方法采用气象站实测的离散气温数据，通过地理插值获取空间上连续分布的气温数据，此方法简单易实现，但受地形、气象站数量和分布及插值方法本身精度的影响，误差较大，且时间分辨率较低。遥感数据具有连续性强、获取速度快和信息量大等优点，但直接利用传感器获取的热红外数据反演气温难度很大[4]，所以一般是利用地表温度(land surface temperature，Ts或LST)、气温和植被指数等参数的统计关系来估计气温[5]。目前，主要有两种方法，一种是温度植被指数法，即TVX(temperature-vegetation index)方法，假设气温与浓密植被冠层温度近似相等，由影像像元窗口中的地表温度和NDVI的负线性关系外推求得饱和NDVI下的地表温度，并作为气温的估计值[2，6-8]。TVX方法的基础是地表温度和NDVI存在着负相关关系，最适用于植被覆盖率较高的地区或季节，而对于植被覆盖率较低或地表温度和NDVI具有正相关性的地区或季节，该方法误差较大；另一种方法则是直接建立地表温度产品和气温的线性回归模型来估计气温，研究表明，地表温度和气温具有较高的相关性，气温可由地表温度线性估计，误差为3℃左右[9-13]。在已有的研究中，很少在建立气温估计模型前分析地表温度和气温的物理关系，利用地表温度估计气温有必要明确其在理论上的可行性。

地表温度指陆地表层的温度，是环境和气候研究的主要变量，是地表物理过程的重要影响因素[14]。现广泛应用的MODIS地表温度产品是根据MODIS传感器31和32热红外波段的数据，通过劈窗算法反演得到[15-16]。本文首先分析地表温度和气温的物理关系，再对两者进行比较和相关分析，分别建立生长季节、非生长季节夜晚地表温度和日最低气温，以及白天地表温度和日最高气温的线性回归模型；然后对模型在相同气象站不同时段、相同时段不同气象站的精度进行验证；最后将验证后的气温估计模型运用于整个研究区，得到新疆典型区内非生长季节的日最低、最高气温分布。本文与大多数研究的不同之处在于将生长季节和非生长季节分开建模，提高了非生长季节的气温估计精度。

2研究区和数据

2.1研究区概况

研究区位于42°N～46°N、83°E～89°E之间的新疆典型区，图1为研究区内2007年3月6日MODIS夜晚地表温度产品，区域内主要包括天山中部和准噶尔盆地两大地形单元。天山中部位于塔里木盆地和准噶尔盆地之间，辽阔复杂的山系，夹着许多山间盆地和纵向构造谷地，地形起伏较大，许多山峰终年积雪，雪线位于4500m～5000m，气候的大陆度和干旱度极强，基本属于干旱荒漠地带[17]。准噶尔盆地位于新疆北部，属于典型温带内陆荒漠性气候，年平均气温为5.4℃，年平均降雨量为100mm，年平均蒸发量为1880mm[18]。

图1　研究区2007年3月6日MODIS夜晚地表温度产品

2.2数据及预处理

2.2.1气象数据

本文以克拉玛依气象站为主要测站，选取乌鲁木齐和石河子两个气象站验证克拉玛依气象站建立的气温估计模型。本文使用的日最低、最高气温数据来自中国气象科学数据共享服务网(http：//cdc.cma.gov.cn/home.do)，是百叶箱内观测到的瞬时最低、最高值，它们的出现时间与水汽蒸发、凝结等大气物理过程的关系十分密切，日最高气温一般在午后2点左右，日最低气温通常出现在清晨日出前后。气温的记录单位为0.1℃，时间分辨率为每日，表1为气象数据信息。

表1　气象数据信息

2.2.2MODIS地表温度产品

本文使用的MODIS地表温度产品是NASA(National Aeronautics and Space Administration)数据服务网站(http：//ladsweb.nascom.nasa.Gov/data/search.html)提供的Terra卫星(过境时刻为10：30am)平台的MOD11A1产品和Aqua卫星(过境时刻为1：30pm)平台的MYD11A1产品。时间序列与气象数据相对应，级别为L3，大小为1200行×1200列，时间分辨率为每日，空间分辨率为1km，投影方式为SIN投影(即等面积的伪圆柱投影)，覆盖面积约为1100km×1100km[19-20]。

2.2.3数据预处理

①坐标转换。采用MRT(MODIS Reprojection Tool)工具将影像由SIN投影坐标系转换为WGS-84经纬度的坐标系。

②提取地表温度。根据经纬度提取各气象站的MOD11A1、MYD11A1夜晚和白天地表温度。

③去除异常值和空缺值。剔除地表温度中明显的异常值和云遮挡引起的空缺值，异常值一般为0℃以下的极其低温值[21]，根据阈值法确定，同时删去对应时间序列的气温数据。

④单位转换。将地表温度由K单位转换成℃单位(t=T-273.15)，同时气温转换到统一量纲(℃)。

数据预处理之后，得到的MOD11A1夜晚Ts、MOD11A1白天Ts、MYD11A1夜晚Ts、MYD11A1白天Ts的有效数据个数分别为216、214、216、200。

3基于地表温度的气温估计方法

3.1地表温度和气温的物理关系

太阳辐射到达地表被吸收后，使地表增温，地表再通过辐射、传导和对流将热量传给空气，这就是空气中热量的主要来源。根据能量守恒定律，地表接收的能量以不同方式转换为其他运动形式，以使能量保持平衡[22]。这一能量交换过程可表示为：

Rn=G+H+LE

(1)

式中，Rn为地表全波段净辐射通量；G为土壤热通量，即下垫面土壤中的热交换；H为感热通量，即下垫面与大气间湍流形式的热交换；LE为潜热通量，即下垫面与大气间水汽的热交换。

地表净辐射通量Rn又称辐射平衡，指地表净得的短波辐射与长波辐射的和，可表示为：

Rn=Rs-Rs↑+RL-RL↑=

(1-α)Rs↓+εaσTa4-εsσTs4

(2)

式中，Rs↓为入射到地表的太阳短波辐射，即太阳总辐射；Rs↑为地表反射的太阳短波辐射，即地表反射辐射；RL↓为来自大气的长波辐射，即大气逆辐射；RL↑为地表发射至大气的长波辐射；α为地表反照率；σ为斯特藩-波尔兹曼常数，等于5.67×10-8W/m2·K4；εa为无云时的大气有效发射率；εs为地表发射率；Ta为参考高度的气温；Ts为地表温度。

土壤热通量G可表示为：

G=(0.1-0.042h)Rn

(3)

式中，h为作物高度，可根据不同的植物类型取值，与叶面积指数LAI和作物覆盖度f有关。

感热通量H又称显热通量，可表示为：

H=ρCp(Ts-Ta)/rac

(4)

式中，ρ为空气密度；Cp为空气定压比热；ρCp表征空气的体积热容量；rac为空气动力学阻力。

潜热通量LE指地表吸收辐射能与蒸发耗热的热交换，又称蒸散，可表示为：

(5)

(6)

联立式(1)至式(6)，整理得到式(7)：

(7)

根据式(7)，地表温度和气温之间具有明确的物理关系，因此，基于地表温度的气温估计方法在理论上是可行的。但是直接应用物理模型式(7)反演气温难度很大，有些参数如空气动力学阻力难以准确确定，考虑到气温的时空分布特征和应用模型对气温数据的需求，气温估计模型由地表温度产品和气温的线性相关关系建立。

3.2地表温度数据和气温数据的关系分析

定义生长季节为5月～10月，非生长季节为11月～次年4月[7]。将2006年5月～2007年4月克拉玛依气象站地表温度和气温进行比较，作出MODIS Ts产品与日最低、最高Ta的时间序列变化趋势图(图2)。可以看出，地表温度和气温的关系在夜晚和白天相差很大；夜晚，地表温度与日最低Ta的一致性较高；白天，尽管地表温度能大致地反映日最高Ta随时间的变化趋势，但两者一致性较低。夜晚和白天产生如此差异的原因是夜晚热红外波段不受太阳辐射的影响，而白天由于太阳辐射的存在使得地表能量平衡系统的交换变得更为复杂。

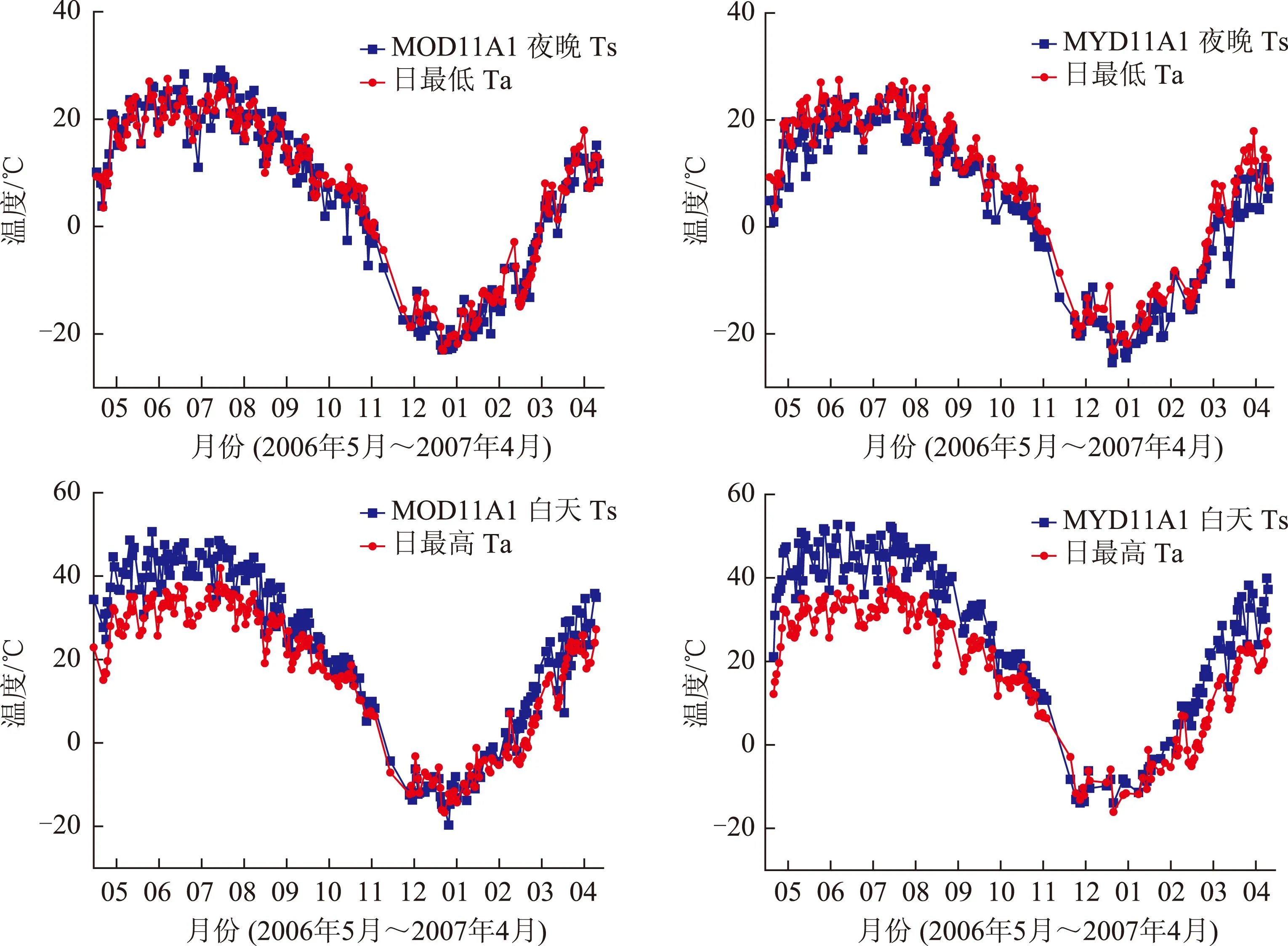
图2　MODIS Ts产品与Ta的时间序列变化趋势

由图2还可看出，MODIS白天Ts与日最高Ta的关系在生长季节和非生长季节有明显差别，在生长季节白天Ts远高于日最高Ta。因此，为提高日最高Ta的估计精度，将数据分为生长季节和非生长季节两部分，进一步分析地表温度和气温的关系，分别计算MODIS夜晚、白天Ts与日最低、最高Ta的统计量(表2)：相关系数R、均方根误差RMSE和绝对平均误差MAE，公式如式(8)、(9)和(10)所示：

(8)

(9)

(10)

由表2可知，MODIS Ts和Ta的相关系数R都高于0.90，且在0.05的显著性水平下通过了t检验，表明MODIS Ts与Ta具有很强的线性正相关性，并且非生长季节的相关关系(≥0.94)更为显著。因此，可以建立MODIS Ts和Ta的回归模型以线性估计Ta，并将生长季节和非生长季节分开建模。

表2　2006年5月～2007年4月克拉玛依气象站

表注：*p<0.05

由于日最低Ta的时刻更接近Aqua卫星的过境时刻(1∶30am)，有学者利用MYD11A2产品(MYD11A1产品8天合成的数据)估计日最低Ta，其RMSE为2.1℃～2.8℃，而用MOD11A2(MOD11A1产品8天合成的数据)产品估计日最低Ta的RMSE为2.3℃～3.3℃，精度比MYD11A2产品的估计精度略低[10]。但也有研究表明，从MOD11A2产品到MYD11A2产品，气温估计精度并没有取得实质性的提高[23]。由表2亦可知，相对于MYD11A1产品，MOD11A1 Ts和Ta的相关系数略高；同时，MOD11A1 Ts和Ta的RMSE和MAE也较小。因此，相对于MYD11A1产品，MOD11A1产品的地表温度数据能更好地估计气温，本文选用MOD11A1产品建立气温估计模型。

3.3气温估计模型的建立

图3为生长季节、非生长季节MOD11A1 Ts产品与日最低、最高Ta的线性拟合，其中图3(a)、(b)分别为生长季节、非生长季节MOD11A1夜晚Ts与日最低Ta的散点分布，图3(c)、(d)分别为生长季节、非生长季节MOD11A1白天Ts与日最高Ta的散点分布，地表温度和气温的线性回归参数如表3。可以看出，非生长季节的点集中分布于拟合直线的两侧，而生长季节点的分布相对较分散，

图3　MOD11A1 Ts产品与Ta的线性拟合

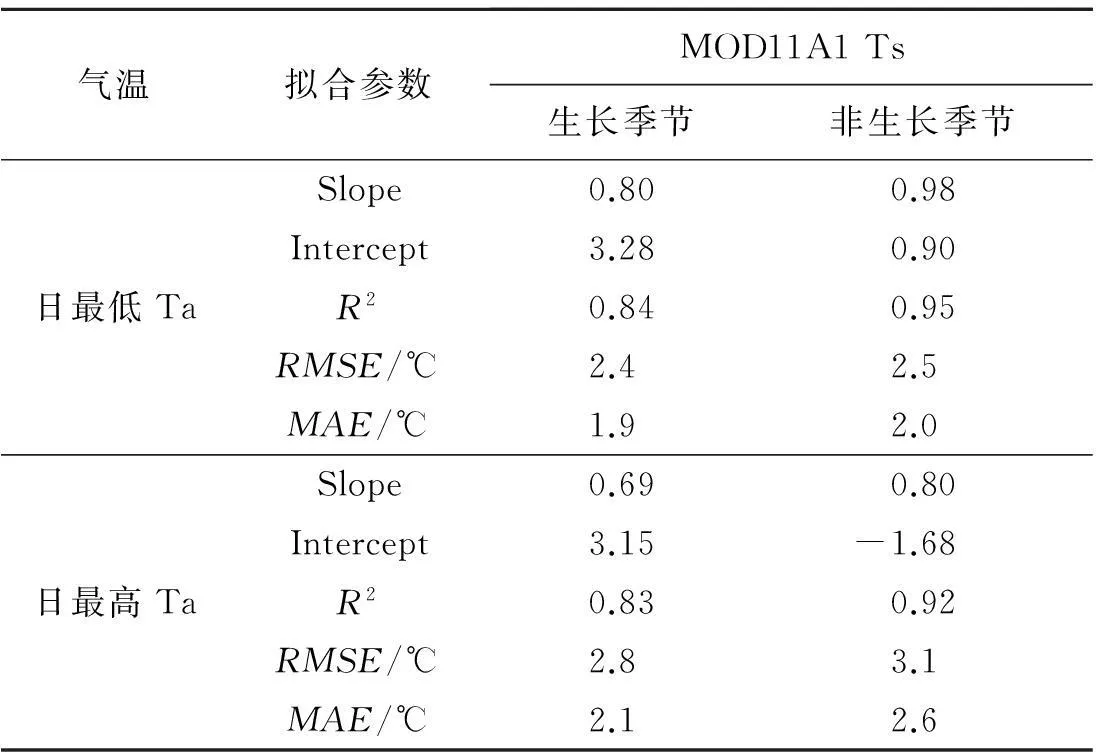
气温拟合参数MOD11A1Ts生长季节非生长季节日最低TaSlope0.800.98Intercept3.280.90R20.840.95RMSE/℃2.42.5MAE/℃1.92.0日最高TaSlope0.690.80Intercept3.15-1.68R20.830.92RMSE/℃2.83.1MAE/℃2.12.6

非生长季节MOD11A1产品与日最低、最高Ta拟合的R2分别为0.95、0.92，而生长季节的R2分别为0.84、0.83，因此，非生长季节MOD11A1产品与气温的拟合优度比生长季节好。由表3可知，气温估计的RMSE为3.0℃左右，MAE小于3.0℃。有学者利用遥感观测数据估计气温，RMSE为3.2℃，MAE为2.5℃，其误差在可允许范围之内[7]。因此这样的精度能够满足研究需要。

生长季节的气温估计模型为：

Ta_min=0.80·Ts_night + 3.28

(11)

Ta_max=0.69·Ts_day + 3.15

(12)

非生长季节的气温估计模型为：

Ta_min=0.98·Ts_night + 0.90

(13)

Ta_max=0.80·Ts_day-1.68

(14)

式中，Ta_min为日最低气温估计值；Ta_max为日最高气温估计值；Ts_night为MOD11A1夜晚地表温度；Ts_day为MOD11A1白天地表温度。

4模型验证

气温估计模型验证包括两步：

(1)相同气象站不同时段的验证

图4为2007年5月～2008年4月克拉玛依气象站的模型验证，其中图4(a)、(b)分别为生长季节、非生长季节日最低Ta的估计值与气象站实际测量值的散点分布，图4(c)、(d)分别为生长季节、非生长季节日最高Ta的估计值与实际测量值的散点分布。图中的对角线为理想拟合直线，另一条则为气温估计值与实际测量值的实际拟合直线，理想拟合曲线和实际拟合曲线的偏离程度反映了拟合的效果。由图可知，所有理想拟合直线和实际拟合直线的偏离程度较小，非生长季节点的分布比生长季节点的分布更集中，非生长季节日最低、最高Ta的估计值和实际测量值拟合的R2为0.95、0.94，而生长季节拟合的R2为0.88、0.81，所以，非生长季节的拟合优度比生长季节好。同时，气温估计的RMSE为3.0℃左右，MAE小于3.0℃，表明构建的模型在同一气象站具有较好的泛化能力。因此，该模型适用于相同气象站不同时段日最低、最高Ta的估计。

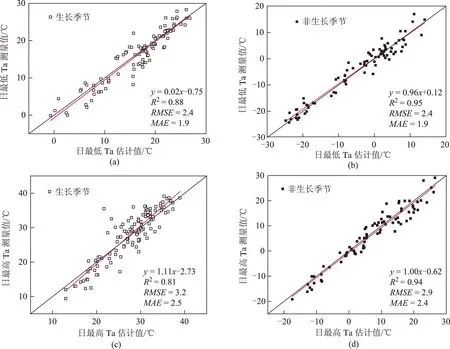
图4　2007年5月～2008年4月克拉玛依气象站验证

(2)相同时段不同气象站的验证

图5是乌鲁木齐气象站的模型验证，由图可知，非生长季节的R2比生长季节高，即非生长季节的拟合优度更好。同时，气温估计的RMSE和MAE都小于3.0℃，取得了较高的精度。因此，该模型适用于乌鲁木齐气象站日最低、最高Ta的估计。

图6为石河子气象站的模型验证，可看出，在生长季节，日最低、最高Ta的估计值和测量值的实际拟合直线与理想拟合直线的偏离程度较大，出现了系统性的偏差，并且日最低Ta估计值高于测量值，日最高Ta低于测量值。根据地表温度的反演原理，地表温度与土地覆盖类型和植被指数密切相关，它们通过影响地表比辐射率直接影响地表温度的变化，因此，在不同的植被指数和土地覆盖条件下，气温和地表温度的关系亦不同[3，24]。植被覆盖度越高，地气温差越小[1]，而石河子地区为农业灌溉区，在生长季节植被覆盖度较高，地气温差较小。然而，夜晚Ts一般低于日最低Ta，白天Ts一般高于日最高Ta[7]。所以，该地区夜晚Ts偏高，白天Ts偏低，从而导致日最低Ta估计值偏高，日最高Ta估计值偏低，与实际测量值出现了系统性的偏差。但是，气温估计在非生长季节取得了较好的结果，RMSE为3.0℃左右，MAE小于3.0℃。因此，建立的气温估计模型在石河子气象站生长季节效果欠佳，但适用于非生长季节的气温估计。

图5　2006年5月～2007年4月乌鲁木齐气象站验证

图6　2006年5月～2007年4月石河子气象站的验证

5研究区气温分布制图

由模型验证结果可知，该气温估计模型在非生长季节取得了较好的结果，拟合优度R2为0.90以上，RMSE在3.2℃之内，MAE在2.8℃之内，因此可将此气温估计模型运用于整个研究区，通过影像镶嵌、投影转换、影响裁剪、气温估计和专题制图等，得到研究区非生长季节的日最低(图7)、最高(图8)气温的连续分布。

图7　研究区非生长季节的日最低气温分布

图8　研究区非生长季节的日最高气温分布

6结束语

本文利用MODIS地表温度产品数据和气象数据，分别建立新疆克拉玛依气象站生长季节、非生长季节的地表温度和气温的线性回归模型，对日最低、最高气温进行了估计，并利用相同气象站不同时段、相同时段不同气象站的数据验证了模型，最后将模型运用于整个研究区，得到研究区内非生长季节的日最低、最高气温分布，得到以下结论：

(1)相对于MYD11A1产品，MOD11A1产品的地表温度数据能更好地估计气温。

(2)该气温估计模型在生长季节效果欠佳。MOD11A1产品估计日最低、最高气温的RMSE在4.6℃之内，MAE在3.8℃之内。

(3)该气温估计模型在非生长季节取得了较好的结果。MOD11A1产品估计日最低气温的RMSE和MAE分别为2.4℃～3.2℃、1.9℃～2.8℃，估计日最高气温的RMSE和MAE则为2.9℃～3.1℃、2.2℃～2.6℃，同时模型在非生长季节的R2为0.91～0.96。

本文虽然取得了较理想的结果，但存在着两个弊端：①MODIS地表温度产品的空间分辨率为1km，提取的气象站的地表温度实际上是1km×1km像元内的面状数据，而气象站提供的是点状气温数据，两者在空间上无法一一对应。当气象站点所在像元满足均质性时，其地表温度可以用面状像元内的平均地表温度表示，但当像元内地表差异较大时，提取的地表温度与气象站点的真实地表温度会存在误差，而这种误差具有不确定性，因此数据源对气温估计精度的影响仍是一个不可避免的问题。②本文建立了一个气象站点的地表温度和气温的线性回归模型，并将此模型运用于整个研究区，默认的前提是研究区内的下垫面是相同的，而该条件一般很难满足，所以导致在地表覆盖差异较大的生长季节误差较大。将来希望在气象站数量较多的研究区，能结合土地覆盖类型、植被指数、大气湿度、地表湿度、气压和风速等因子进行建模。

参考文献：

[1]柯灵红，王正兴，宋春桥，等.青藏高原东北部MODIS地表温度重建及其与气温对比分析[J].高原气象，2011，30(2)：277-287.

[2]PRIHODKO L，GOWARD S N.Estimation of air temperature from remotely sensed surface observations[J].Remote Sensing of Environment，1997，(60)：335-346.

[3]韩秀珍，李三妹，窦芳丽.气象卫星遥感地表温度推演近地表气温方法研究[J].气象学报，2012，70(5)：1107-1118.

[4]CZAJKOWSKI K P，GOWARD S N，STADLER S J，et al.Thermal remote sensing of near surface environmental variables：Application over the oklahoma mesonet[J].The Professional Geographer，2000，52(2)：345-357.

[5]董良鹏.基于MODIS地表温度的气温估计方法及其在中国东部城市群热岛效应研究中的应用[D].南京：南京信息工程大学，2012.

[6]STISEN S，SANDHOLT I，NORGAARD A，et al.Estimation of diurnal air temperature using MSG SEVIRI data in west africa[J].Remote Sensing of Environment，2007，(110)：262-274.

[7]ZHU W B，LU A F，JIA S F.Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products[J].Remote Sensing of Environment，2013，(130)：62-73.

[8]徐永明，覃志豪，沈艳.基于MODIS数据的长江三角洲地区近地表气温遥感反演[J].农业工程学报，2011，27(9)：63-68.

[9]MOSTOVOY G V，KING R.Using MODIS LST data for high-resolution estimates of daily air temperature over mississippi[J].In Proceedings of the 3th International Workshop on the Analysis of Multi-Temporal Remote Sensing Images，2005，76-80.

[10]VANCUTSEM C，CECCARO P，DINKU T，et al.Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over africa[J].Remote Sensing of Environment，2010，(114)：449-465.

[11]FU G，SHEN Z X，ZHANG X Z，et al.Estimating air temperature of an alpine meadow on the northern tibetan plateau using MODIS land surface temperature[J].Acta Ecologica Sinica，2011，(31)：8-13.

[12]LIN S P，MOORE N J，MESSINA J P，et al.Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east africa[J].International Journal of Applied Earth Observation and Geoinformation，2012，(18)：128-140.

[13]YAO Y H，ZHANG B P.MODIS-based air temperature estimation in the southeastern tibetan plateau and neighboring areas[J].Journal of Geographical Sciences，2012，22(1)：152-166.

[14]于文凭，马明国.MODIS地表温度产品的验证——以黑河流域为例[J].遥感技术与应用，2011，26(6)：705-712.

[15]WAN Z M，DOZIER J.A Generalized split-window algorithm for retrieving land-surface temperature from space[J].IEEE Transactions on Geoscience and Remote Sensing，1996，34(4)：892-905.

[16]WAN Z M，LI Z L.A Physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data[J].IEEE Transactions on Geoscience and Remote Sensing，1997，35(4)：980-996.

[17]苏宏新.全球气候变化条件下新疆天山云杉林生长的分析与模拟[D].北京：中国科学院植物研究所，2005.

[18]王晶，吕昭智，钱翌，等.新疆准噶尔盆地典型荒漠区不同景观植被对土壤养分的影响[J].中国沙漠，2010，30(6)：1367-1373.

[19]吕京国，张小咏，蒋玲梅，等.MODIS地标产品数据的相关算法及处理过程[J].遥感信息，2009，24(8)：25-29.

[20]WAN Z M.Collection-5 MODIS land surface temperature products users’ guide[EB/OL].http：//www.icess.ucsb.edu/modis/LstUsr Guide/MODIS_LST_products_Users_guide_C5.pdf，2007-3.

[21]NETELER M.Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data[J].Remote Sensing，2010，(2)：333-351.

[22]赵英时.遥感应用分析原理与方法[M].北京：科学出版社，2003.

[23]MOSTOVOY G V，KING RL，REDDY K R，et al.Statistical estimation of daily maximum and minimum air temperatures from MODIS LST data over the state of mississippi[J].GIScience and Remote Sensing，2006，43(1)：78-110.

[24]齐述华，王军邦，张庆员，等.利用MODIS遥感影像获取近地层气温的方法研究[J].遥感学报，2005，9(5)：570-575.

E-mail：lfl2009zzu@sina.com