基于卡尔曼滤波的Landsat-8卫星影像几何精校正

基于卡尔曼滤波的Landsat-8卫星影像几何精校正

郭少锋1，2，李安1，李山山1，冯钟葵1

(1.中国科学院遥感与数字地球研究所，北京 100094；2.中国科学院大学，北京 100049)

摘要：卡尔曼滤波是一种递推线性最小方差估计算法，被广泛应用于GPS动态数据处理、组合导航和通信与信号处理等领域。本文将卡尔曼滤波引入卫星影像几何精校正处理中，以Landsat-8卫星影像为例，利用卡尔曼滤波方法和地面控制点构建运动方程和测量方程，实现了对卫星星历和姿态数据的修正。实验证明，相比于传统最小二乘平差法，该方法使用较少的控制点即可达到稳定的精度，降低了几何精校正对控制点数量的依赖，具有较高适用性。

关键词：Landsat-8；卡尔曼滤波；几何精校正

doi:10.3969/j.issn.1000-3177.2015.01.003

中图分类号：TP751文献标识码：A

收稿日期：2013-11-28修订日期：2014-03-06

基金项目：江西省数字国土重点实验室开放基金(DLLJ201303)；航空遥感技术国家测绘地理信息局重点实验室经费资助项目(2014B02)。

作者简介：于英(1985～)，男，博士，主要研究基于移动平台的视频遥感图像快速处理方法。

Geometric Precision Correction of Landsat-8 Imagery Based on Kalman Filter

GUO Shao-feng1，2，LI An1，LI Shan-shan1，FENG Zhong-kui1

(1.InstituteofRemoteSensingandDigitalEarth，ChineseAcademyofSciences，Beijing100094；

2.UniversityofChineseAcademyofSciences，Beijing100049)

Abstract：Kalman filter is a recursive linear minimum variance estimation algorithm，and it has been widely used in GPS dynamic data processing，integrated navigation，communication and signal processing fields.This paper applies kalman filter into geometric precision correction of Landsat-8 imagery，and completes the correction of satellite ephemeris and attitude data.In the experiments，the comparison of accuracy between kalman filter algorithm and least square method shows that the application of kalman filter in precision correction of landsat-8 imagery can reduce the dependence of GCPs.

Key words：Landsat-8；kalman filter；geometric precision correction

1引言

随着航天技术、传感器技术和计算机技术的蓬勃发展，遥感技术在近30年取得了很大的进步，并被越来越广泛地应用于国民经济建设中。为了适应多层次、多角度、全方位和全天候的全球立体对地观测的要求，近两年世界遥感强国相继发射了众多遥感卫星。其中，美国为了延续Landsat系列卫星的对地观测任务，于2013年2月11日成功发射Landsat-8卫星。该卫星分辨率为30m，卫星重访周期为16天，带有OLI和TRIS两个对地观测传感器。地物变化监测成为其最重要的研究目标之一，这对卫星的定位精度提出了较高的要求，因此针对Landsat-8图像进行几何精校正处理十分重要。

几何精校正主要通过地面控制点来建立遥感图像与地面之间的精确关系，利用数学平差方法，校正由于卫星星历数据、姿态数据等测量误差造成的卫星图像的几何误差[1]。Yoichi提出了一种双向扫描型传感器几何校正的方法，分别用高低频分离方法建立了正扫和反扫视点模型以此校正几何误差[2]；Kratky等对共线方程加入轨道约束条件，提出了基于轨道约束的严格成像几何模型[3]；Gruen等从航测角度出发，对SPOT影像应用共线方程，并开发出光束法平差模式求解卫星外方位元素，其校正精度可以达到亚像元级[4]；张过等人将有理函数模型应用于推扫式光学卫星影像的几何精校正中，平原影像纠正精度达到2个像元以内，山区达到3个像元以内[5]。上述方法建立校正模型后，都是基于最小二乘的平差方法解算卫星图像的几何误差。

对于Landsat-8卫星的几何精校正，待估参数包括卫星三维位置和速度、卫星三维姿态及其变化率，所以建立最小二乘平差模型，至少需要6个以上的控制点，若获得稳定的几何精校正精度，则需要更多分布均匀、数量充足的地面控制点作为多余观测参与平差过程。而对于Landsat系列遥感卫星，一方面，地面采集控制点获取的成本较高，尤其对于偏远地区，人力、物力成本也相应增加[6]；另一方面，中分辨率(30m)影像在进行目视解译或自动匹配同名点时，达到较高匹配精度更加不易。为了解决上述问题，本文提出了采用卡尔曼滤波的方法来进行Landsat-8卫星的几何精校正。实验证明，基于卡尔曼滤波的Landsat-8几何精校正减少了对控制点数量的依赖，取得了较好的精校正效果。

2基本原理及其实现

2.1卡尔曼滤波的基本原理

卡尔曼滤波是一种递推线性最小方差估计算法。它的基本思想是以最小均方误差为最佳估计准则，采用信号与噪声的状态空间模型，在不同状态变化过程中，利用前一状态的估计值和当前状态的观测值来更新状态变量的估计，求出当前状态的估计值。算法根据系统方程和测量方程，对需要处理的状态矢量做出满足最小均方误差的估计[7]。

卡尔曼滤波不但计算简便，运算速率快，而且在误差模型具体形式不确定的情况下，仍然具有适用性。因此，该算法在平稳的动态运动系统中已经被广泛应用，尤其在GPS动态数据处理、组合导航和通信与信号处理等领域得到了深入的研究和应用[8-10]。

2.2基于卡尔曼滤波的Landsat-8几何精校正原理

在遥感卫星成像过程中，卫星状态空间的变化可以近似与时间线性相关。因此卡尔曼滤波在修正遥感卫星状态方面也具有适用性，梁泽环论证了将卡尔曼滤波应用于SPOT卫星几何精校正的可行性[11]，Shin等采用扩展卡尔曼滤波进行ATSR图像几何精校正能够达到一个像元内的几何精度[12]。本文提出用卡尔曼滤波算法进行Landsat-8影像几何精校正。

将卡尔曼滤波应用于Landsat-8卫星几何精校正的总流程如图1所示。在控制点数据和系统级校正的结果图像匹配之后，利用卡尔曼滤波建立卫星星历数据和姿态数据的运动方程和测量方程，通过引入控制点，将系统级几何校正后的星历数据和姿态数据中存在的系统误差进行修正，并最终处理得到几何精校正的结果。

图1　基于卡尔曼滤波的Landsat-8卫星影像 几何精校正总流程

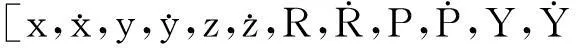
图2　基于卡尔曼滤波的Landsat-8几何精校正具体流程

基于卡尔曼滤波的Landsat-8几何精校正是一个迭代求解过程，其计算分为3个过程：预估过程、校正过程与迭代过程。

预估过程：建立运动方程，利用K状态下Landsat-8卫星状态矢量的估计值及对应的误差协方差矩阵进行预估，计算K+1状态下Landsat-8卫星状态矢量的预测值及对应的误差协方差矩阵。

校正过程：该过程分为两部分：①建立测量方程。在K+1状态下，利用Landsat-8卫星状态矢量预测值及对应的误差协方差矩阵和引入的控制点坐标，求出该状态下的卡尔曼增益；②建立更新方程。利用Landsat-8卫星状态的预测值、引入的控制点坐标及卡尔曼增益，求解K+1状态下Landsat-8卫星状态矢量的估计值及对应的误差协方差矩阵。

迭代过程：若K+1状态下的Landsat-8卫星状态矢量的变化量低于预设阈值，则迭代终止，并利用该状态下的卫星状态矢量获得精确几何校正模型文件，处理得到精校正结果；否则，加入新的控制点，令K=K+1，将其作为下一状态的输入值，重复进行预估过程和校正过程。在实际应用中，迭代过程往往采用控制点个数控制迭代次数，作为迭代结束条件，在本文中采用了此做法。

2.3基于卡尔曼滤波的Landsat-8几何精校正关键技术

基于卡尔曼滤波的Landsat-8几何精校正算法包括3个基本方程：运动方程、测量方程和更新方程。其中，运动方程对应预估过程，测量方程和更新方程对应校正过程。

2.3.1运动方程

运动方程用于Landsat-8几何精校正中不同状态下的卫星状态矢量的转换，是预估过程的主要方程。运动方程利用K状态下Landsat-8卫星状态矢量的估计值及其误差协方差，推算K+1状态Landsat-8卫星状态矢量的预测值及其误差协方差，其过程如图3所示。

卫星状态矢量的预测值计算公式为：

X(K+1/K)=φ(K+1/K)·X(K/K)+

G(K+1)·W(K+1)

(1)

式中，X(K+1/K)是由K状态下卫星状态矢量的估计值预测得到的K+1状态下卫星状态矢量的预测值，φ(K+1/K)是由K状态到K+1状态的转移矩阵，X(K/K)是K状态下卫星状态矢量的估计值，W(K+1)是白噪声向量，G(K+1)是噪声矢量系数。

预测值的误差协方差矩阵计算公式为：

P(K+1/K)=φ(K+1/K)·P(K/K)·

φ(K+1/K)T+Q(K+1)

(2)

式中，P(K+1/K)是X(K+1/K)对应的误差协方差矩阵，P(K/K)是K状态下X(K/K)对应的误差协方差矩阵，X(K/K)是噪声的协方差矩阵。

图3　运动方程

运动方程形式的推导不涉及到几何处理过程，仅与卫星动力学方程和姿态动力学方程相关[11]。转移矩阵包括两部分：与卫星星历有关的部分和与卫星姿态有关的部分，其形式推导的流程如图4所示。

卫星动力学方程是基于万有引力定律和开普勒卫星运动三定律，在地心惯性坐标系下建立的。由于建立的方程是矢量方程，需要将矢量方程分解为坐标系3个方向上的分量组成方程组，并求解方程组的通解，最后经过简化后，得到由K状态预测K+1状态的转移矩阵中与星历有关的矩阵部分φ(K+1/K)ephemeris，其形式如下：

(3)

式中，tK是引入的第K个控制点对应的Landsat-8影像同名点的成像时刻与景中心成像时刻的时间差，控制点同名像点的成像时刻从控制点匹配文件中读取，景中心成像时刻从系统级校正结果文件中获取；ω0是Landsat-8卫星在惯性坐标系下的角速度，其数值可在Landsat-8卫星参数文件中获取。

姿态动力学方程基于刚体的动量矩定理建立，即刚体对惯性空间某固定点的角动量的变化率，等于作用于刚体的所有外力对此点力矩的总和。同样，将矢量方程分解为3个方向上的分量方程，建立方程组，求解方程，可得由K状态预测K+1状态的转移矩阵中与星历有关的矩阵部分φ(K+1/K)attitude，其形式如下：

(4)

式中，tK和ω0的含义和来源与式(3)相同。

由K状态预测K+1状态的转移矩阵φ(K+1/K)形式如式。

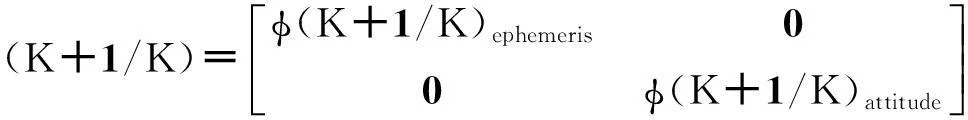
结合式(3)和式(4)，即：

(5)

2.3.2测量方程

测量方程的作用是联系卫星状态矢量和控制点坐标，利用测量矩阵，将运动方程中获得的当前状态下Landsat-8卫星状态矢量的预测值，转化为大地坐标系下控制点坐标的计算值。其过程如图5所示。

图5　测量方程

(6)

测量矩阵H(K)中的元素，可根据其定义直接导出[13]。

H(K)=

(7)

式中，(x,y,z)是引入的控制点在地心坐标系的坐标值，(φ,λ)是引入的控制点大地经纬度，其数值都可以从控制点匹配结果文件中获取；B是Landsat-8卫星轨道倾角，h是Landsat-8卫星的地面高度，两者的数值都可在Landsat-8卫星参数文件中获取。

2.3.3更新方程

更新方程的作用，是根据运动方程中获得的当前状态下Landsat-8卫星状态矢量的误差协方差矩阵和测量矩阵计算当前状态的卡尔曼增益，并利用当前状态下，运动方程中得到的Landsat-8卫星状态矢量的预测值和控制点大地坐标测量值，计算该状态下Landsat-8卫星状态矢量的估计值及误差协方差矩阵，处理过程如图6所示。

Kg(K+1)=P(K+1/K)·H(K+1)T/

{H(K+1)·P(K+1/K)·H(K+1)T+R(K+1)}-1

(8)

X(K+1/K+1)=X(K+1/K)+Kg(K+1)·

(9)

P(K+1/K+1)=P(K+1/K)-Kg(K+1)·

H(K+1)·P(K+1/K)

(10)

式(8)中Kg(K+1)为K+1状态下的卡尔曼增益，R(K+1)是白噪声矩阵；式(9)中X(K+1/K+1)是该状态下卫星状态矢量的估计值，Z(K+1)是该状态下引入的控制点大地坐标测量值；式(10)中P(K+1/K+1)是X(K+1/K+1)对应状态下卫星状态矢量的误差协方差矩阵。

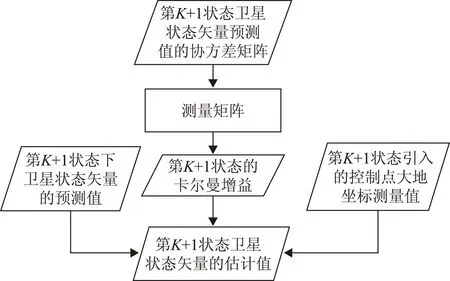
图6　更新方程

2.4实现步骤

选取Landsat-8卫星影像景中心时刻的卫星星历和姿态数据，作为Landsat-8卫星状态矢量预测值的初始值，此时，K初始值为0。

②利用协方差矩阵P(K+1/K)和测量矩阵H(K+1)计算出卡尔曼滤波的增益值Kg(K+1)。

③将卡尔曼滤波增益Kg(K+1)带入到更新方程中，利用第K+1状态下Landsat-8卫星状态矢量预测值X(K+1/K)和控制点大地坐标的测量值Z(K+1)，求出第K+1状态下Landsat-8卫星状态矢量的估计值X(K+1/K+1)及其对应的误差协方差矩阵P(K+1/K+1)。

④判断算法终止条件，若迭代结束，则可将误差校正后的星历及姿态数据生成几何精校正模型文件，再通过后续处理获得几何精校正图像；若不满足迭代结束条件，则令K=K+1。

⑤计算转移矩阵，将其带入运动方程中，利用第状态下Landsat-8卫星状态矢量的估计值预估第状态下Landsat-8卫星状态矢量的预测值，并求出相应的误差协方差矩阵，并转入①继续迭代过程。

3实验与讨论

实验处理了多景Landsat-8卫星图像，限于篇幅本文选取了其中两景Landsat-8卫星的图像数据的实验做介绍。第一景图像对应地理范围内的主要地形为平原，第二景图像对应地理范围内的主要地形为山地。两景Landsat-8卫星的图像数据分别在不同控制点数量的条件下，利用卡尔曼滤波算法进行几何精校正，并将该算法与传统最小二乘平差法进行几何精校正的算法做比较。两景Landsat-8卫星图像信息及选取的控制点信息如表1所示。精度评价所使用的50个检查点来自GLS2005控制点库[14]。

两组数据中，为说明卡尔曼滤波在迭代过程中误差修正的效果，将每次迭代处理生成结果图像，均利用检查点计算RMSE(均方根误差)，评价精校正精度。

表1　实验图像和控制点信息表

在两个实验数据的图像中选取的控制点的分布情况如图7和图10所示。

图7　数据一选取控制点分布图

在不同的控制点引入顺序下，基于卡尔曼滤波的Landsat-8图像几何精校正结果图像的精度随控制点引入个数变化情况如表2、表3和表4所示。基于卡尔曼滤波算法的和最小二乘法的Landsat-8图像几何精校正结果图像的精度随控制点引入个数变化情况的对比如图8、图9和图11所示。其中，控制点为0时表示初始输入系统级校正图像的几何精度。

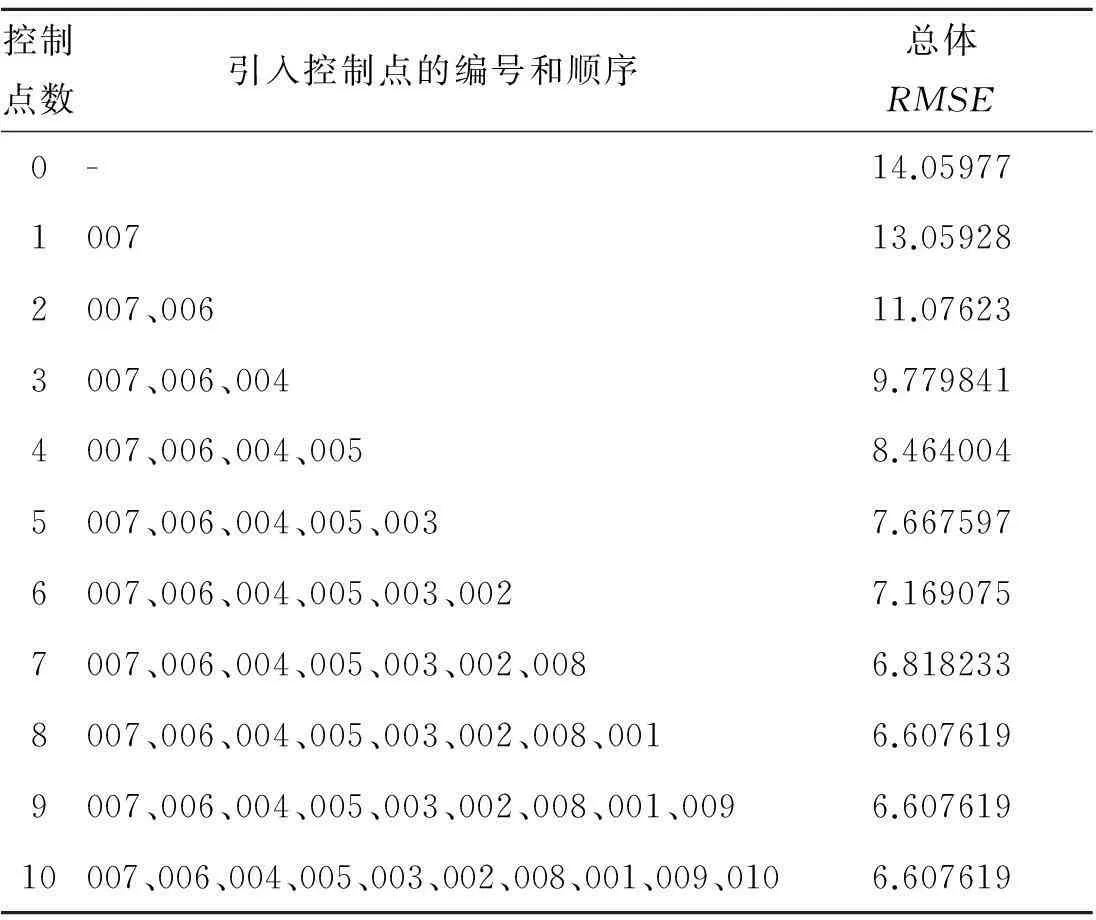
表2　数据一卡尔曼滤波算法结果图像精度随控制点

图8　数据一中两种算法结果图像精度与控制点 个数关系对比图一

控制点数引入控制点的编号和顺序总体RMSE0-14.05977100913.0743292009、00311.0854123009、003、0079.7813644009、003、007、0018.4539875009、003、007、001、0057.6759416009、003、007、001、005、0047.1713687009、003、007、001、005、004、0106.8204658009、003、007、001、005、004、010、0026.6081269009、003、007、001、005、004、010、002、0086.60761910009、003、007、001、005、004、010、002、008、0066.607619

图9　数据一中两种算法结果图像精度与控制点 个数关系对比图二

对比表2和表3可知，基于卡尔曼滤波的Landsat-8几何精校正结果精度与控制点的引入顺序无关。如图9，图10和图11所示，最小二乘算法由于受到参数个数估计限制，至少需要7个控制点才能进行计算。相比而言，卡尔曼滤波算法则不受控制点个数的限制，随着控制点个数增加，误差减少，校正精度逐渐提高。当平原区控制点数达到8个(山地区控制点数达到10个)时，图像精度已基本趋于稳定，其精度较系统级几何校正精度提高40%以上，相较于最小二乘平差法，精度平均提高20%以上。当控制点数目继续增加时，卡尔曼滤波算法结果的精度已经无明显变化，而最小二乘算法结果误差仍未达到最低。最终，当最小二乘方法引入22个控制点时，精校正精度趋于稳定，并与卡尔曼滤波算法结果精度相当，表明卡尔曼滤波算法收敛速度快于最小二乘法。

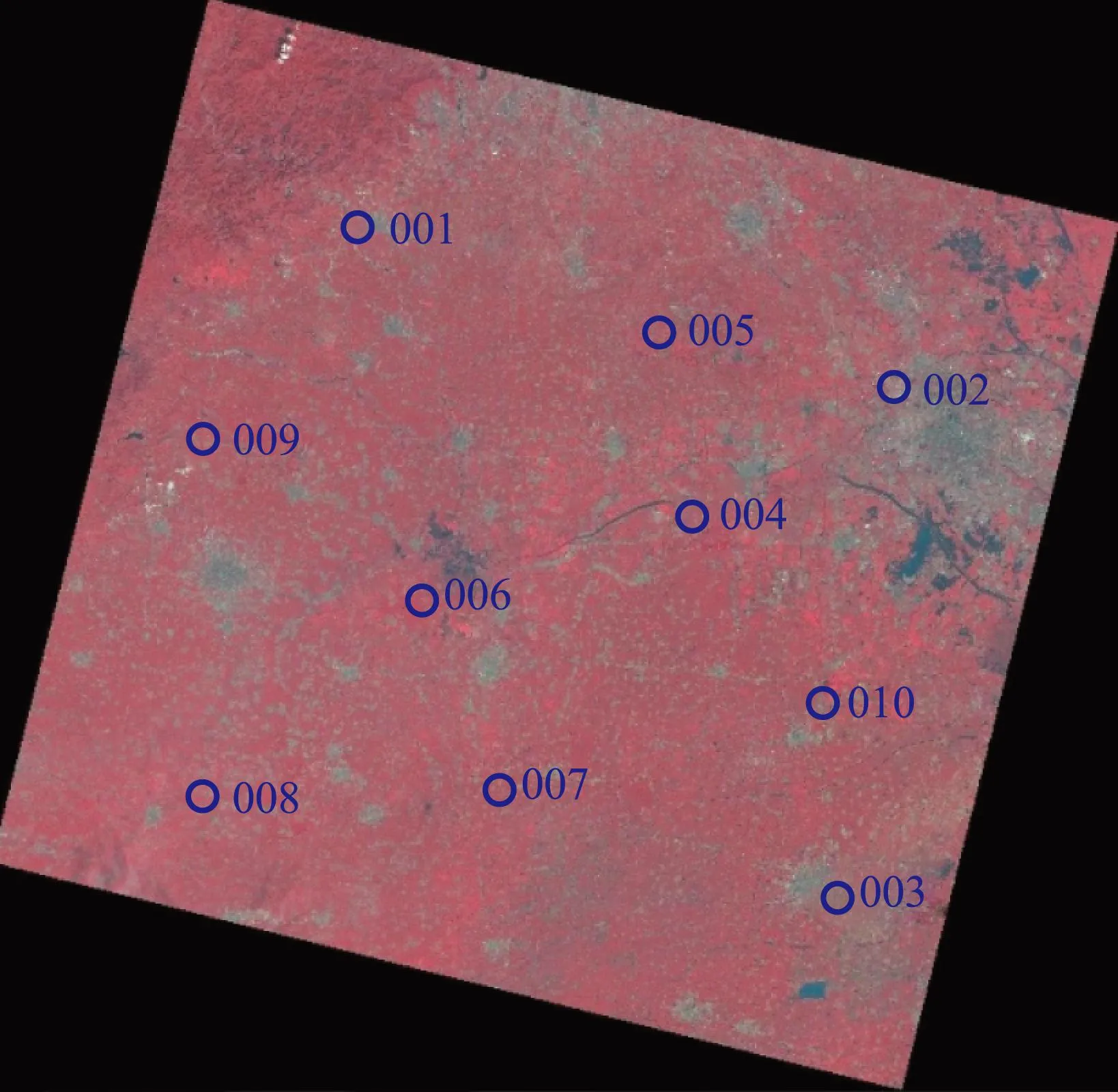
图10　数据二选取控制点分布图

控制点数引入控制点的编号和顺序总体RMSE0-22.66217100819.410992008、00217.187773008、002、00115.442784008、002、001、00913.590875008、002、001、009、01012.031256008、002、001、009、010、00610.285557008、002、001、009、010、006、0038.7645378008、002、001、009、010、006、003、0047.7732069008、002、001、009、010、006、003、004、0077.10131010008、002、001、009、010、006、003、004、007、0056.620061

图11　数据二中两种算法结果图像精度与 控制点个数关系对比图

4结束语

Landsat-8卫星数据几何精校正中，本文将卡尔曼滤波算法用于卫星姿态及星历中的误差校正。实验证明，当控制点匹配正确且分布均匀时，当其数目低于7个时，基于卡尔曼滤波的几何精校正方法能够获得较系统级校正结果精度更高的几何校正结果。随着控制点引入数目的增多，在迭代结束，定位精度稳定情况下，基于卡尔曼滤波的几何精校正较传统最小二乘算法达到误差最小时的速度更快，且结果的校正精度相当。因此，基于卡尔曼滤波的Landsat-8卫星影像的几何精校正较传统最小二乘平差方法有效降低了对控制点数量的依赖，并且适用于不同地形条件。理论上，对于其他遥感卫星，如果能够提供算法所需要的参数，此几何精校正技术也同样适用于该卫星的几何精校正。

参考文献：

[1]孙家抦.遥感原理与应用(第二版)[M].武汉：武汉大学出版社，2009.

[2]YOICHI S，HOMMA K，KOMURA F.Geometric correction algorithms for satellite imagery using a bi-directional scanning sensor[J].Geoscience and Remote Sensing，1991，29(2)：292-299.

[3]KRATKY V.Rigorous photogrammetric processing of SPOT images at CCM Canada[J].ISPRS Journal of Photogrammetry and Remote Sensing，1989，(44)：53-71.

[4]GRUEN A.Potentian and limitation of high resolution satellite imagery[C].The 21stAsian Conference on Remote Sensing，Taipei，2000.

[5]张过，李扬，祝小勇，等.有理函数模型在光学卫星影像几何纠正中的应用[J].航天返回与遥感，2010，31(4)：51-57.

[6]肖倩，冯钟葵，李山山.GLS2005控制点库介绍及应用[J].遥感信息，2013，28(5)：59-63.

[7]彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊，2009，8(11)：32-34.

[8]秦永元，张洪钺，汪淑华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，2012.

[9]王力循.无迹Kalman滤波在IMU和GPS组合导航系统中的应用研究[D].南昌：南昌大学，2010.

[10]邱凤云.Kalman滤波理论及其在通信与信号处理中的应用[D].济南：山东大学，2008.

[11]梁泽环.卡尔曼滤波在卫星遥感影像大地校正中的应用[J].环境遥感，1990，5(4)：297-307.

[12]SHIN D，POLLARD J K，MULLER J P.Accurate geometric correction of ATSR images[J].IEEE Transactions on Geoscience and Remote Sensing，1997，35(4)：997-1006.

[13]ARNOLD P.Application of a recursive distortion estimator to the geodetic correction of THEMATIC MAPPER imagery[C].Machine Processing of Remotely Sensed Data Symposium，332-385.

[14]肖倩，冯钟葵，李山山.GLS2005控制点库介绍及应用[J].遥感信息，2013，28(5)：59-63.

E-mail：yuying5559104@163.com