气泡破裂产生膜液滴理论模型的建立与验证
2016-01-11马超,薄涵亮
气泡破裂产生膜液滴理论模型的建立与验证
马超1,薄涵亮2
(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都610041;
2.清华大学 核能与新能源技术研究院,北京100084)
摘要:本文研究了常温、常压条件下自由液面单气泡破裂产生膜液滴现象。在明确该过程物理机理及气泡破裂环状物模型基础上,应用瑞利射流不稳定性分析理论结果,通过合理假设,建立了自由液面单气泡破裂产生膜液滴的物理模型。通过引入瑞利断裂时间判据,对时间变量进行离散,数值求解该理论模型,可获得气泡破裂产生膜液滴的初始参数,包括膜液滴数量、尺寸、速度、初始位置。将模型计算结果同已有实验数据对比,二者符合较好,证明了模型的正确性。
关键词:蒸汽发生器;气泡破裂;膜液滴;理论模型
中图分类号:TL333 文献标志码:A
收稿日期:2014-06-27;修回日期:2015-01-31
作者简介:马超(1987—),男,辽宁铁岭人,工程师,博士,核科学与技术专业
doi:10.7538/yzk.2015.49.11.2036
Establishment and Verification of Theoretical Model
of Film Drops Produced by Bubble Bursting
MA Chao1, BO Han-liang2
(1.ScienceandTechnologyonReactorSystemDesignTechnologyLaboratory,
NuclearPowerInstituteofChina,Chengdu610041,China;
2.InstituteofNuclearandNewEnergyTechnology,TsinghuaUniversity,Beijing100084,China)
Abstract:The phenomenon of the film drops produced by the bubble bursting at a free water surface under the normal temperature and pressure conditions was researched in this paper. While the physical mechanism of this phenomenon was clear, based on the previous ring theory model and the Rayleigh instability analysis theory, a new model of the film drops produced by bursting bubble at the free surface was established under some reasonable assumptions. Using time variables discrete method, mathematical model was solved and the film drop initial parameters were obtained, including the number, diameter, velocity and direction, and initial position. The model calculation results fit well with the previous experimental data, justifying the correctness of the new model.
Key words:steam generator; bubble bursting; film drop; theory model
压水堆蒸汽发生器二次侧水在传热运动过程中,在两相界面由于机械打碎及气泡破裂产生大量的小液滴,这些小液滴如果不能除去而被饱和蒸汽流夹带进入二回路,将会造成管道关闭件卡死及汽轮机叶片的汽蚀,最终影响电厂运行及机组寿命[1]。因此,核电厂设计要求蒸汽发生器出口处湿度不能高于0.25%,针对蒸汽流中液滴夹带问题的研究成为汽水分离装置设计过程的核心环节[2]。
对于浮动气泡在自由液面处破裂产生膜液滴过程的物理机理目前已较为明确[3-10]。膜液滴产生模型中,要解决的核心问题是确定不稳定射流变化规律。由于真实气泡破裂过程中射流情况复杂,很难应用一个模型同时描述,因此,需借助合理的假设条件对真实情况进行简化。
本文以Spiel[8]建立的环状物模型为基础建立气泡破裂产生膜液滴模型,通过质量守恒确定环状物上射流体积分布规律,对射流进行圆柱规则简化,应用瑞利低速不稳定射流断裂结论,计算环状物上不稳定射流断裂产生的膜液滴初始参数[11-12]。
1理论模型
1.1假设条件
本文建立的理论模型的假设条件如下:1) 膜液滴产生过程中不计重力影响;2) 液膜卷曲过程中厚度均匀;3) 气泡曲率半径保持不变;4) 气泡破裂点位置随机产生;5) 射流间隔为固定值λ,λ=9e,其中e为环状物临界半径;6) 射流在产生及断裂过程中为规则圆柱体,不发生弯曲变形;7) 某时刻射流长度矢量方向为该时刻射流顶部速度方向;8) 流体无黏性不可压缩,忽略周围空气剪切作用;9) 液体与气体均处于热平衡状态,无传热、传质现象发生。
1.2球面液膜与水面分离
膜液滴仅是由自由液面以上的液帽部分破裂产生,同时由于液帽部分是球面,在假设液膜厚度均匀、不计重力,并且破裂过程中液帽曲率半径不发生改变的条件下,可不考虑水面及破裂点位置的影响,抽象出一完整球面液膜,对完整球面液膜建立膜液滴产生模型。然后根据破裂点相对位置及自由液面气泡浮动几何关系,通过坐标变换把计算结果同自由液面叠加,如果产生膜液滴空间位置处在水面以下,则对其除去,还原恢复到真实物理情况。
根据Toba气泡浮动理论,通过输入物性参数(表面张力、密度)及气泡的体积就能得到气泡浮动的几何形状,包括气泡破裂产生膜液滴过程最重要的几何参数:液帽曲率半径R和液帽边缘半径rj[13]。
基于高速摄像可视化实验观察结果及前人理论分析可知,由于边缘颈缩及边缘对流现象的存在,使得液膜表面厚度发生起伏,破裂点在液帽球面部分任意位置均可产生,因此破裂点位置是一随机变量[3,10]。由于浮动气泡在自由液面上为轴对称形状,液帽球面边缘至对称轴距离为rj,破裂点至对称轴距离为rb,定义随机变量BP=rb/rj为气泡破裂点相对位置。通过大量气泡破裂实验,统计纯水中曲率半径R=2.8~28.7 mm范围内1 589个气泡的破裂点相对位置。针对实验统计结果给出破裂点相对位置的概率密度分布函数,该分布函数设定各分区内破裂点产生概率满足均匀分布,分区积分概率满足实验中气泡破裂点相对位置频率统计值,概率密度曲线如图1所示。
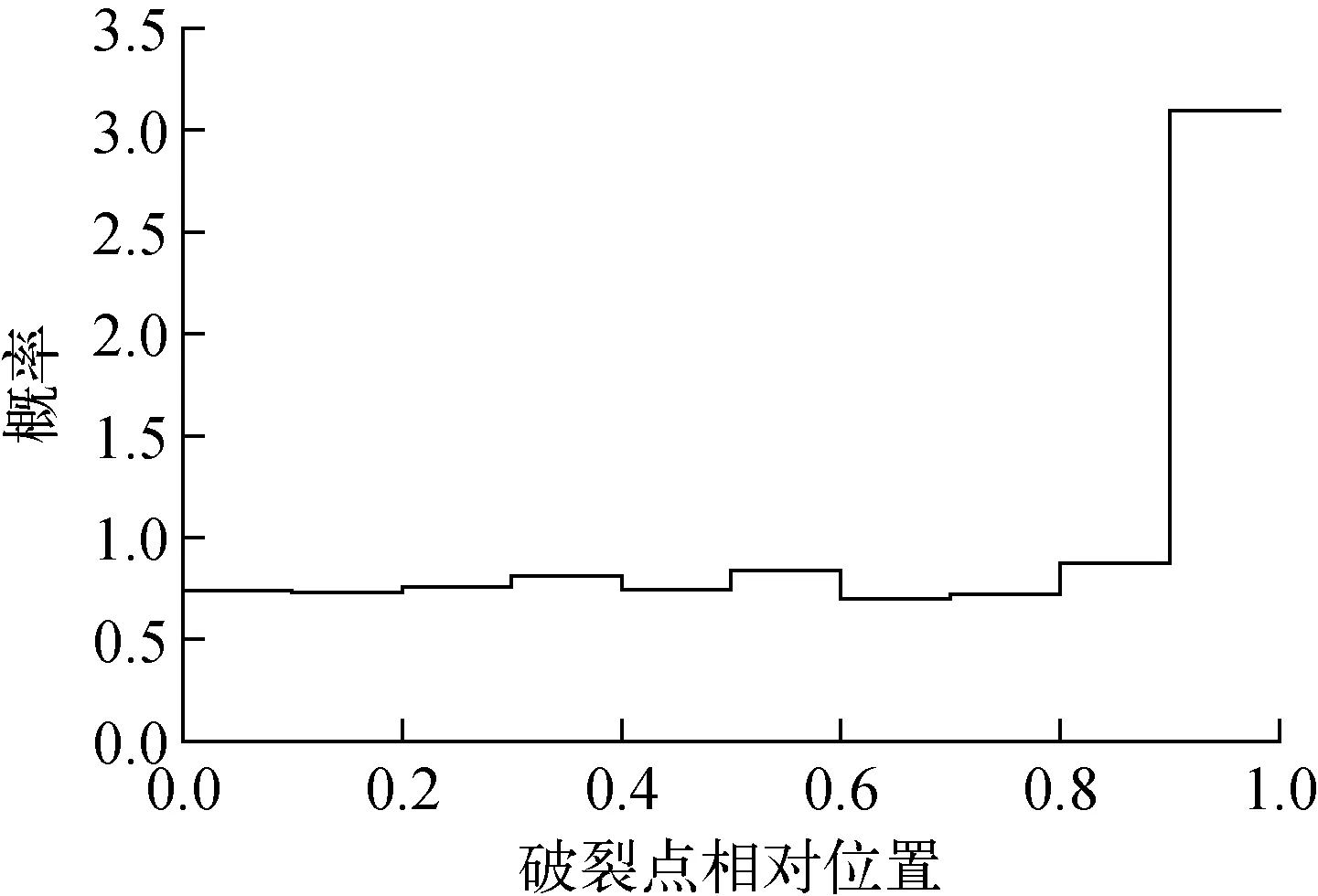
图1 气泡破裂点相对位置的概率密度分布曲线 Fig.1 Probability density distribution curve of bubble break point relative position
在明确气泡浮动几何形状及破裂点位置的情况下,需抽象出球面液膜且确定自由液面方程。抽象球膜与真实液帽坐标转化示意图如图2所示,首先建立完整球膜破裂坐标系x-y-z,球面球心即为原点O,破裂点固定位于B点(0,0,R),根据后续的子模型对其进行膜液滴产生情况计算,得到完整球膜破裂产生膜液滴的信息。

图2 抽象球膜与真实液帽坐标转化示意图 Fig.2 Schematic of coordinate transformation between hypothetical and real situations
给定气泡曲率半径R,根据气泡浮动理论可确定出气泡液帽边缘半径rj;同时由破裂点相对位置概率密度函数自动随机生成气泡破裂点相对位置BP;由BP=rb/rj确定出气泡破裂点半径BC=rb。为简化起见,认为自由液面平行于y轴,其法线为OC,由此可求解出在x-y-z坐标下,水面O1A方程为:
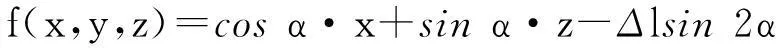
(1)
α=arcsin(rb/R)∈[0,arcsin(rj/R)]
(2)
(3)
如果液滴初始位置坐标为P(x,y,z),若满足f(x,y,z)>0则表示该液滴位于水面之上;若满足f(x,y,z)≤0则表示该液滴位于水面之下,应予以除去。
根据水面方程建立真实物理情况下液帽破裂坐标系x1-y1-z1,由于球面对称性,破裂点相对位置分布函数只同轴向z1位置有关,考虑破裂点只发生在平面。将坐标系x-y-z内的液滴位置转化到x1-y1-z1中去,变换关系为:
(4)
1.3环状物射流分布规律
根据Spiel的环状物模型,环状物在球面液膜上做匀速圆周运动,当其经过某一临界仰角φc时,表面张力不能维持向心力,环状物发生不稳定性射流,并且此后环状物平均半径保持恒定为e[8]。某一时间间隔内转化为不稳定射流的流体总体积等于液膜消失部分体积与环状物体积增量之差。由于假设环状物上不稳定射流产生时刻相互间距为定值λ=9e,各条射流在方位角方向对称分布、体积相等,因此单一射流体积等于总体射流体积除以射流数量,射流基点即为环状物(抽象为环线)同射流所在方位角平面的交点。随着环状物周长变化,射流数量发生相应的增减,射流对应的方位角发生改变,射流体积重新分配。在仰角φc≤φ≤90°范围内,环状物周长不断增大,当环状物周长变化量为1个λ时,射流发生分岔现象,射流数目增加;在仰角90°≤φ≤180°范围内,环状物周长不断减小,当环状物周长变化量为1个λ时,射流发生归并现象,射流数目减少。由此可获得射流体积、方位角位置、仰角位置随时间的变化。
液膜破裂时的临界厚度是膜液滴产生模型中的一项重要参数,目前不能直接测量,只能先进行液膜卷曲速度的测量,再根据液膜厚度同卷曲速度的关系式进行间接确定。在高速摄像可视化实验中,通过大量实验数据得到液膜卷曲速度u同气泡曲率半径间的经验关系式为[14]:
(5)
其中,R的单位取为mm,u的单位取为m/s。
(6)
其中:σ为表面张力系数,N/m;ρ为液膜密度。
针对抽象完整球膜环状物进行分析:建立球坐标系,球心设为坐标原点,破裂发生时φ=0、r=R,因此破裂点在球坐标下坐标变换为(R,0,0)。设破裂点周围液膜发生卷曲形成环状物所经过的球面仰角为φ,方位角坐标为θ,径向坐标为r,则环状物所吸收的液膜体积V为:
(7)
由于液膜厚度相对气泡曲率半径非常小,引入近似条件:
R2dr=R2Δr=R2h
(8)
对环状物体积进行积分得到:
(9)
单位长度环状物体积Vl为:
Rh(1-cosφ)/sinφ
(10)
单位长度环状物质量Ml为:
Ml=2σR(1-cosφ)/u2sinφ
(11)
失稳条件为单位长度环状物维持圆周运动所需向心力Fl大于表面张力[7]:
Fl=Mlu2/R>2σ
(12)
Spiel[8]在可视化实验中观察φc≈35°。因此,失稳时刻射流数量N为:
N=Int(2πRsinφc/λ)
(13)
其中,Int表示取整数。
由于假设在射流变化断裂过程中表面张力系数不变,液膜卷曲速度不变,因此环状物在达到临界仰角φc=35°之后,其半径e不再改变,由环状物定义得到单位长度环状物质量为:
(14)
得到环状物半径同气泡曲率半径间的关系式:
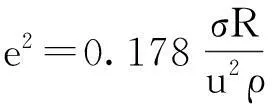
(15)
经过临界仰角之后,液膜消失体积同环状物体积增量之差完全转变为不稳定性射流体积,由于假设在产生时刻各条射流相互间隔一定、均匀分布,因此同一时刻各条射流体积相等。设不发生珠化断裂现象时的射流体积(即等效射流体积)为Vj,由质量守恒条件可得:
2πRsinφ·hRdφ-2πRcosφ·πe2dφ=NdVj
(16)
设射流产生时刻为初始时刻,对应环状物临界仰角为φc=35°,则:
(17)
其中,35°≤φ≤180°。对式(17)积分得到射流体积随时间t的变化规律:
(18)
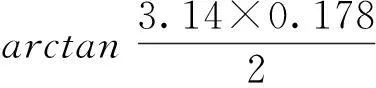
(19)
当射流发生归并或分岔时,射流数量发生改变,射流体积重新分配。
1.4射流断裂产生膜液滴
由于任意时刻射流对称分布,原三维问题可转化为二维平面问题,只考虑某射流所在方位角平面内膜液滴产生情况,对射流应用Sallam等[11]的体积圆柱规则化经验关系式,求得任意时刻射流等效长度与直径。根据瑞利射流断裂理论[12]及Lhuissier等[3]的实验结果,引入射流断裂时间判据,通过对时间变量离散求解射流断裂过程,获得射流断裂产生膜液滴的尺寸、速度及初始位置。最终添加自由液面控制方程,对产生液滴结果进行修正,如果液滴初始位置位于液面之下,不符合真实情况,予以去除。
图3示出射流体积圆柱规则化过程示意图。依据Sallam等[11]的液柱表面射流产生实验结果,将射流形状规则化为圆柱体,忽略射流弯曲变形,并给出完整射流长度(未断裂产生液滴部分)同射流等效直径间的无量纲经验关系式:
Lj/dj=0.59We0.32=0.59(ρu2dj/σ)0.32
(20)

图3 射流体积圆柱规则化过程示意图 Fig.3 Schematic of jet volume cylindrical regularization
其中:Lj为射流长度;dj为直径;We为韦伯数,We中的特征速度取为环状物匀速圆周速度。射流圆柱体积Vj为:
(21)
任意时刻下,根据射流体积Vj计算射流长度Lj和直径dj。
(22)
(23)
其中,c1=0.801,c2=0.193,c3=0.398。
在低速射流断裂理论中引入射流断裂时间,即表示单射流从产生到射流断裂产生第1颗液滴的时间tb,满足tb=cτ,其中c为经验系数,τ为瑞利特征断裂时间,其表达式为:
(24)
Lhuissier等[3]通过实验观察给出纯水中气泡环状物射流断裂时间经验关系式tb=9.546τ。根据该经验关系式,在膜液滴产生模型中引入射流断裂时间判据,该判据同两个时刻有关,射流当前时刻tn及液滴预发时刻tp。液滴预发时刻tp的定义表述为:对于即将产生的液滴,其体积离开环状物开始进入射流的时刻,对于射流第1次断裂产生的液滴,预发时刻即为环状物刚经过临界角度,不稳定射流开始形成时刻。当射流当前时刻与预发时刻之差满足时间判据关系tn-tp≥cτn时,判定发生射流断裂,产生膜液滴。
图4为圆柱射流断裂产生液滴示意图。由于初始射流直径dj、速度uj稳定,射流断裂长度为定值Lj,射流产生时从基点z=0处喷出,该过程中不断受到表面不稳定扰动波的作用,当射流顶部运动到z=Lj处时,射流开始发生断裂,产生液滴,断裂时间即为tb=Lj/uj=cτ。由于圆柱射流断裂产生液滴的尺寸相同,假设射流体积以离散液滴状态存在,射流刚产生时刻为第1颗液滴的预发时刻tp1,当射流体积刚好等于第1颗液滴体积时,即为第2颗液滴的预发时刻tp2,以此类推,射流中体积为前m-1颗液滴总体积的时刻,即为第m颗液滴预发时刻tpm,若此时第1颗液滴刚好到达射流断裂位置z=Lj,射流当前时刻tn=tpm,则该时刻满足断裂时间判据关系式:
(25)
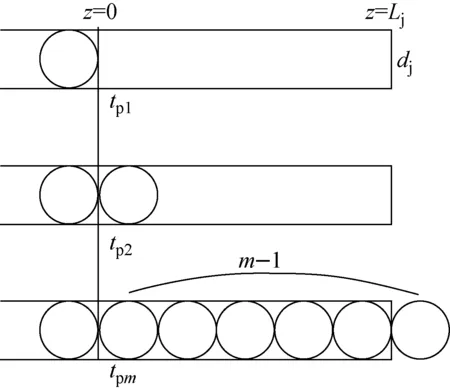
图4 射流断裂产生液滴示意图 Fig.4 Schematic of jet breaking producing drop
与圆柱射流断裂情况不同,对于环状物上产生的不稳定射流,其直径dj是时间的函数,而瑞利特征时间同射流直径有关,因此τ也是当前时刻的函数。
(26)
其中,djn为射流等效直径。
对于膜液滴产生过程,需要对时间离散,进行数值求解,计算每一时层射流的几何参数,判断该时层是否发生射流断裂。每次发生断裂后,通过射流体积同时间的关系式计算下一颗液滴的预发时刻,同时将射流体积减去已断裂液滴体积。
由于环状物表面的不稳定射流属于低速射流,按瑞利经典理论,断裂液滴直径dd为射流等效直径djn的1.9倍,即dd=1.9djn[12]。因此,断裂产生膜液滴的体积为:
(27)
相同体积液滴在射流中时所具有的表面积为:
(28)
断裂液滴产生后所具有的表面积为:
(29)
忽略重力、黏性耗散作用,动能的减少转化为表面能的增加,该过程能量守恒方程为:
(30)
其中,ud为断裂液滴初始速度。定义断裂前后速度比为ε=ud/u,则有:
(31)
每当发生射流断裂时,通过物性参数及当前时刻射流等效直径djn、速度u,即可计算断裂液滴的速度。
膜液滴初始速度方向及位置示意图示于图5。由于假设流体无黏性,射流中即将产生断裂液滴的流体质量不受周围流体介质的影响。依据惯性,射流顶端速度即为预发时刻环状物圆周运动的矢量速度u=u(cosφp,-sinφp),其中φp为预发时刻环状物仰角,速度方向沿着球面切向,液滴速度方向同射流顶端速度的相同。射流长度为当前时刻射流等效长度Ln,射流顶端矢量可表示为Ln=Ln(cosφp,-sinφp)。射流基点矢量长度为R,该时刻为仰角φn,该矢量可表示为R=R(sinφn,cosφn),沿径向方向向外。因此发生断裂时刻,膜液滴初始位置即为射流顶端位置,是射流基点球面半径与射流长度的矢量和:
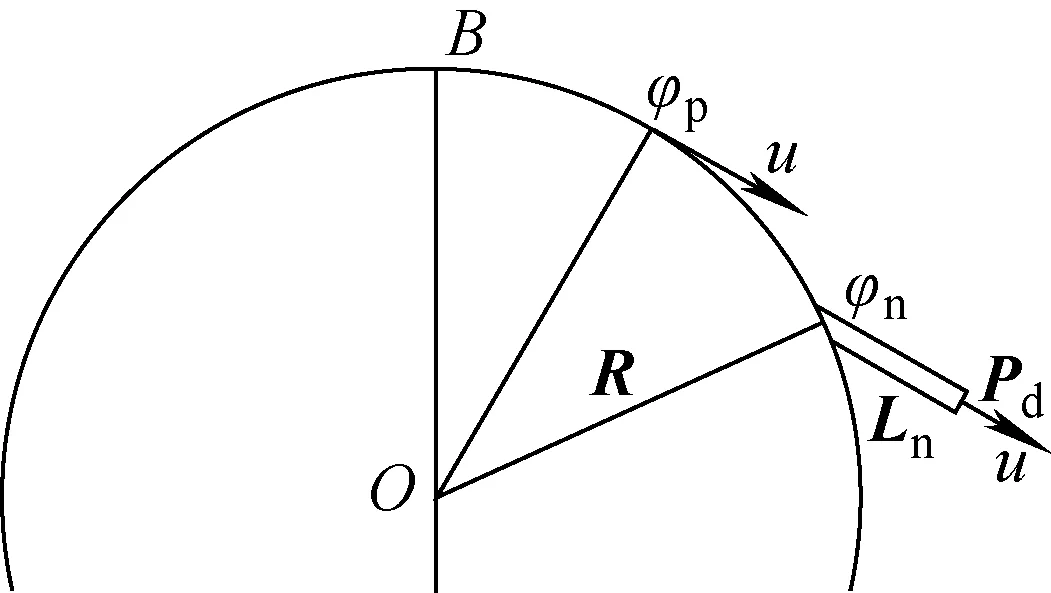
图5 膜液滴初始速度方向与位置示意图 Fig.5 Schematic of initial velocity and position of film drop
1.5模型求解
该模型通过对时间变量离散的方法进行数值求解[14],伪代码表述如下。
1) 初始参数输入:根据气泡几何参数、物性参数、临界仰角、破裂点相对位置(根据破裂点相对位置概率分布函数随机生成)计算液膜卷曲速度、液膜临界厚度、环状物半径、射流间距等物理量。
2) 时间离散化:设定时间步长Δt,初始时层n=0,时间t=nΔt,计算环状物周长和射流数量,对第1颗膜液滴预发时刻进行初始化tp=0。
3) 外部循环:仰角是否仍在(0°,180°)范围内。
4) 内部循环:判断该时层是否发生射流归并或分岔,若发生,射流数目增减,体积平均分配。
5) 射流规则化处理:计算该时层射流几何参数。
6) 时间判断:判据式(25)是否成立,如果成立发生射流断裂,计算膜液滴直径、速度、初始位置,输出结果并更新计算下一颗液滴预发时刻。
7) 时层更新:n=n+1,计算新时层时间、仰角、环状物周长、射流数量,内循环结束。
8) 外循环结束。
9) 水面控制方程:处理膜液滴输出结果,水面下膜液滴予以除去,还原为真实情况。
10) 膜液滴产生结果输出存盘。
11) 程序结束。
2模型验证
为验证该模型的正确性,选取前人在不同流体中进行的膜液滴产生实验结果进行对比[5,8-9]。图6示出纯水中气泡破裂产生的膜液滴数量与平均直径。图7示出海水中气泡破裂产生的膜液滴数量与平均直径。
由于实验结果均为多次破裂平均值,理论计算中每个尺寸气泡计算20次破裂结果后取平均值。最终得到相应条件下不同尺寸气泡破裂产生膜液滴数量、平均直径的计算结果。由图6a、图7a可见,理论计算值与实验数据变化趋势一致,膜液滴数量随气泡曲率半径的增大而增多,理论计算值高于实验中测量到的液滴数量。由图6b、图7b可见,理论计算值同实验数据变化趋势一致,膜液滴平均直径随气泡曲率半径的增大而增大,理论计算值低于实验中测量到的液滴平均直径。这是由于模型建立过程中,假设液膜厚度均匀,而实际物理过程中,液膜厚度在重力作用下从液帽顶部到液帽边缘逐渐增大,液膜厚度增大使得环状物半径变大,不稳定射流数量减少、直径增大,导致膜液滴尺寸增大,因此理论计算值比实验中测量到的膜液滴数量更多,平均直径更小。
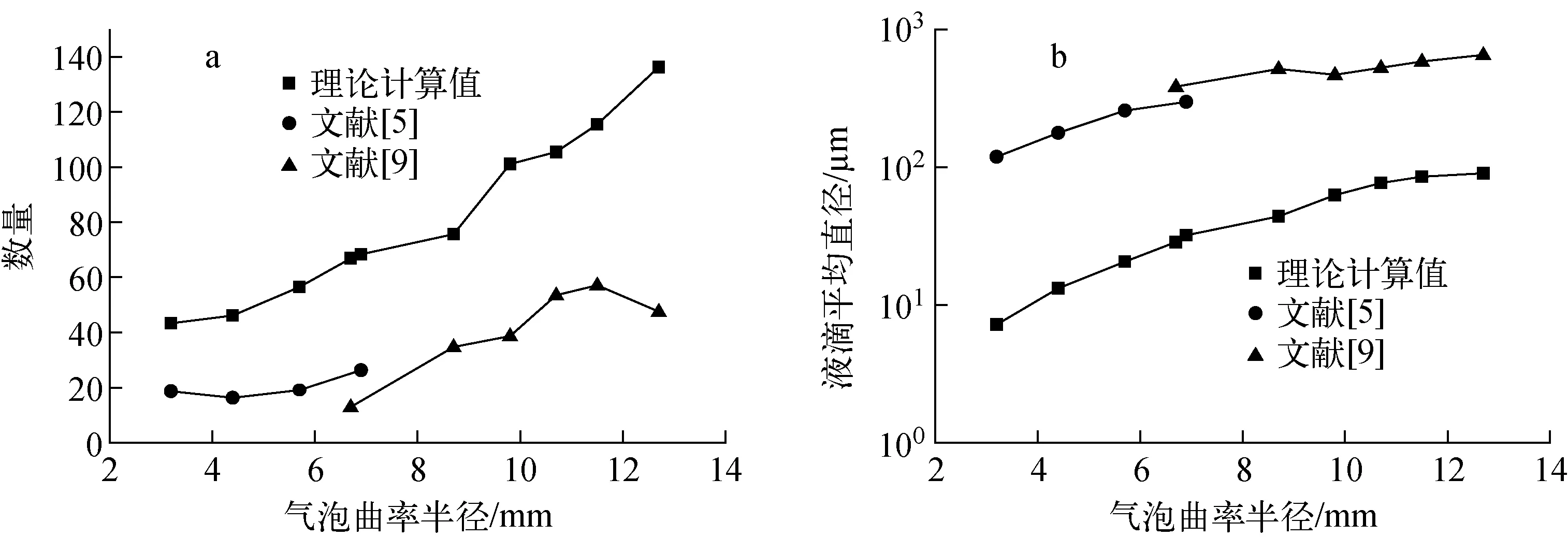
图6 纯水中气泡破裂产生的膜液滴数量与平均直径 Fig.6 Number and mean diameter of film drops produced by bursting bubble in pure water

图7 海水中气泡破裂产生的膜液滴数量与平均直径 Fig.7 Number and mean diameter of film drops produced by bursting bubble in sea water
3结束语
本文在明确气泡破裂产生膜液滴的物理现象基础上,在合理假设前提下,对真实气泡破裂产生膜液滴现象进行抽象简化,通过将球面液膜与自由水面分离再叠加、确定环状物表面射流分布、引入断裂时间判据的方法,建立起气泡破裂产生膜液滴模型。通过时间离散化方法数值求解膜液滴产生时刻的初始信息。通过将该理论计算结果同已有实验数据对比,符合良好,证明该模型在常温、常压条件下的正确性。
该理论模型现仍较为粗糙,较多应用简化假设有待于进一步加强,接下来的工作可从以下几方面进行:
1) 考虑重力对液膜厚度空间分布的影响。真实情况下,液膜厚度并非均匀,液膜厚度分布直接影响液膜卷曲速度,进而影响膜液滴的尺寸分布与初始速度分布。
2) 考虑气体流场对于破裂过程的影响。分析气泡破裂过程中液帽曲率半径的变化,气泡内外压强变化驱动产生的气体流场对于环状物运动及射流断裂过程的影响。
3) 本文中气泡破裂产生膜液滴实验研究及理论模型研究均建立在常温、常压条件下,同实际蒸汽发生器高温、高压工况有差别。应用单气泡破裂产生膜液滴模型估算蒸汽发生器内膜液滴产生情况,需进一步对该模型进行修正,考虑高温、高压环境对于模型假设条件与计算结果的影响。
参考文献:
[1]张谨奕. 三维流场中单液滴运动模型和应用研究[D]. 北京:清华大学核能与新能源技术研究院,2012.
[2]李宋恒. 电站锅炉汽水分离装置的原理和设计[M]. 北京:水利水电出版社,1986.
[3]LHUISSIER H, VILLERMAUX E. Bursting bubble aerosols[J]. Journal of Fluid Mechanics, 2012, 696: 5-44
[4]BLANCHARD D C, SYZDEK L D. Film drop production as a function of bubble-size[J]. Journal of Geophysical Research-Oceans, 1988, 93(C4): 3 649-3 654.
[5]RESCH F, AFETI G. Film drop distributions from bubbles bursting in seawater[J]. Journal of Geophysical Research-Oceans, 1991, 96(C6): 10 681-10 688.
[6]RESCH F, AFETI G. Submicron film drop production by bubbles in seawater[J]. Journal of Geophysical Research-Oceans, 1992, 97(C3): 3 679-3 683.
[7]SPIEL D E. A hypothesis concerning the peak in film drop production as a function of bubble size[J]. Journal of Geophysical Research-Oceans, 1997, 102(C1): 1 153-1 161.
[8]SPIEL D E. On the births of film drops from bubbles bursting on seawater surfaces[J]. Journal of Geophysical Research-Oceans, 1998, 103(C11): 24 907-24 918.
[9]马超,薄涵亮. 气泡破裂产生膜液滴现象可视化实验研究[J]. 原子能科学技术,2012,46(增刊):231-235.
MA Chao,BO Hanliang. Visualization study of film drops produced by bubble bursting[J].Atomic Energy Science and Technology, 2012, 46(Suppl.): 231-235(in Chinese).
[10]MA Chao, BO Hanliang. Experimental observations of the spacial distribution of film drops produced by bursting bubbles on a free liquid surface[J]. Journal of Tsinghua University: Science and Technology, 2013, 53(9): 1 310-1 314.
[11]SALLAM K, DAI Z, FAETH G. Turbulent primary breakup of round and plane liquid jets in still air, AIAA-2002-1115[R]. [S. l.]: [s. n.], 2002.
[12]RAYLEIGH L. On the stability of cylindrical fluid surfaces[J]. Philos Mag, 1892, 34: 177-180.
[13]TOBA Y. Drop production by bursting of air bubbles on the sea surface, ii: Theoretical study on the shape of floating bubbles[J]. OceanogrSocJapan, 1959, 15: 121-130.
[14]马超. 自由液面单气泡破裂产生膜液滴现象实验与理论研究[D]. 北京:清华大学核能与新能源技术研究院,2014.
