基于抽样方法的特征值不确定度分析

基于抽样方法的特征值不确定度分析

万承辉1，曹良志1，吴宏春1，祖铁军1,*，沈炜1,2

(1.西安交通大学 核科学与技术学院，陕西 西安710049;

2.加拿大核安全委员会，加拿大 渥太华K1P 5S9)

摘要：核数据是反应堆物理计算的基础数据，研究其不确定度对反应堆物理计算引入的不确定度，对提高反应堆的安全性和经济性具有重要意义。本文基于抽样理论研究了反应堆物理计算不确定度分析的方法，研发了不确定度分析程序UNICORN。基于ENDF/B-Ⅶ.1评价数据库，使用NJOY程序开发了多群协方差数据库。采用UNICORN程序和多群协方差数据库对三哩岛燃料棒和基准题RB31的k∞进行了不确定度分析，得到核数据库中各分反应道截面的不确定度对k∞造成的不确定度。结果表明：238U(n,γ)截面对三哩岛燃料棒k∞造成的不确定度最大，相对不确定度达0.4%左右；协方差数据库的不同来源会对不确定度分析结果造成一定影响。

关键词：不确定度分析；抽样方法；核数据库

中图分类号：TL32 文献标志码：A

收稿日期：2014-07-29;修回日期：2014-10-14

基金项目：国家自然科学基金资助项目(91226106)；863计划资助项目(2013AA051402)；上海核工程研究设计院资助项目

作者简介：万承辉(1991—)，男，江西南昌人，硕士研究生，核科学与工程专业

doi：10.7538/yzk.2015.49.11.1954

*通信作者：祖铁军，E-mail: tiejun@mail.xjtu.edu.cn

Eigenvalue Uncertainty Analysis Based on Statistical Sampling Method

WAN Cheng-hui1, CAO Liang-zhi1, WU Hong-chun1, ZU Tie-jun1,*, SHEN Wei1,2

(1.SchoolofNuclearScienceandTechnology,Xi’anJiaotongUniversity,Xi’an710049,China;

2.CanadianNuclearSafetyCommission,OttawaK1P 5S9,Canada)

Abstract:The nuclear data are the basic data for reactor physics calculation. It is significant to study the contribution of their uncertainty to the uncertainty of reactor physics calculation for improving the safety and economy of reactor. Based on the ENDF/B-Ⅶ.1library, the covariance library including the variance and covariance for all the basic cross sections and all the groups was generated using the NJOY code. The uncertainty analysis code UNICORN for reactor physics calculation was developed based on the statistical sampling method. Based on the UNICORN and covariance library, the uncertainties of k∞ for Three Mile Island (TMI) lattice and RB31 benchmark, due to the uncertainty of basic cross sections, were analyzed. The results indicate that the uncertainty of 238U(n, γ) cross section is the largest uncertainty to the k∞ of TMI lattice and the relative uncertainty to the k∞ is up to about 0.4%, and different sources of covariance library effect the uncertainty of analysis result.

Key words：uncertainty analysis; statistical sampling method; nuclear library

不确定度分析可给出计算结果的分布范围和置信度，对提高反应堆安全性和经济性具有重要意义。核数据会对反应堆燃料棒k∞计算结果引入0.4%～0.5%的不确定度[1]。近年来，国际上采用抽样方法进行了大量的研究，研发的程序有DINOSAUR[2]、SCALE-SS[3]和MCNP/TMC[4]等，研究内容涉及组件计算和燃耗计算等。相比之下，国内在该领域内的研究工作与国际存在较大差距，亟需对此开展深入研究。本文拟基于抽样理论研究反应堆物理计算不确定度分析的方法，研发不确定度分析程序。

1不确定度分析计算模型

1.1抽样方法计算模型

采用抽样方法对任意多输入多响应系统进行不确定度分析，包括3个主要计算步骤[5]：由协方差数据描述输入参数的分布；抽样产生输入参数的样本空间；采用输入参数样本计算获得对应的响应结果，并统计产生响应的不确定度。任意多输入多响应系统可表示为：

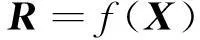
(1)

其中:R=[R1,R2,…,RnR]T为响应向量，nR为系统响应数；X=[x1,x2,…,xnX]T为输入参数向量，nX为系统输入参数数。

1) 描述输入参数分布

为对输入参数进行抽样，首先需确定每个输入参数xi(i=1,2,…,nX)的分布空间和联合概率密度函数。由于许多实际问题的变量均服从或近似正态分布[6]，因此，设输入参数X服从维度为nX、均值向量为μ(μ=[μ1,μ2,…,μnX]T)、协方差矩阵为Σ的nX元正态分布，即X～NnX(μ,Σ)。Σ表示为：

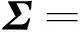
(2)

式中，cov(xi,xj)(i,j=1,2,…,nX)为输入参数xi和xj之间的协方差。均值向量μ和协方差矩阵Σ可用于确定输入参数的分布空间。此时，输入参数的联合概率密度函数g(X)表示为：

(3)

输入参数之间相互独立，即协方差矩阵Σ的非对角元素为零的条件下，联合概率密度函数g(X)可表示为：

(4)

由式(4)可看出，相互独立参数的联合概率密度函数等于各输入参数的概率密度函数的乘积。

2) 产生输入参数计算样本

根据输入参数的分布空间和联合概率密度函数g(X)，通过抽样方法产生输入参数计算样本空间XS。在输入参数X存在相关性，即不相互独立时，直接产生满足联合概率密度函数g(X)的输入参数计算样本，需考虑具有协方差信息的输入参数之间的协同变化，存在较大的技术难度。此时，可通过对相互独立参数抽样的方法实现对相关参数的抽样[6]。设相互独立参数为Y=[y1,y2,…,ynX]T，并服从维度为nX、均值向量为零向量、协方差矩阵为单位矩阵的nX元标准正态分布，即Y～NnX(0,I)。对于任意独立参数yi(i=1,2,…,nX)，均满足yi～N(0,1)。此时，Y的联合概率密度函数表示为：

(5)

通过对相互独立参数Y的每个参数yi(i=1,2,…,nX)进行单独抽样，再组成样本空间的方法，就可产生其样本空间YS。利用相互独立参数Y的样本空间YS，通过如下的公式[2]即可获得相关的输入参数X的样本空间XS：

(6)

产生的样本空间XS为：

(7)

其中：nS为每个输入参数抽取的样本数；xi,j(i=1,2,…,nX；j=1,2,…,nS)为输入参数xi的第j个计算样本。样本空间YS产生过程中，本文采用先进的LHS(latin hypercube sampling)抽样技术[7]，既保障样本能覆盖整个参数的分布空间，同时也保障每个样本出现的概率相同，方便后续统计学计算分析。

3) 统计样本计算结果

将式(7)所示的计算样本空间XS作为系统的输入，计算不同输入参数样本条件下的响应结果Ri(i=1,2,…,nS)。对任意响应Rj(j=1,2,…,nR)进行统计，分别计算得到其期望和标准差信息：

(8)

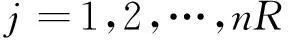
(9)

其中：E(Rj)为响应Rj(j=1,2,…,nR)的期望值；V(Rj)为响应Rj(j=1,2,…,nR)的标准差，即响应的不确定度。利用式(8)、(9)即可获得响应的不确定度，并定义标准差V(Rj)与期望值E(Rj)的比值为相对不确定度。

中子输运方程是一典型的多输入多输出的计算方程，其多群形式[8]可表示为：

(10)

式(10)中各物理量意义见文献[8]。由式(10)可知，中子输运方程的输入参数包括反应道截面、几何条件和材料组成等；输出变量包括keff和通量分布等。在采用抽样的方法研究截面的不确定度对反应堆物理计算的keff造成的不确定度时，可将式(10)写成如下输入和响应的表达形式：

(11)

即在输入参数X=[σ1,σ2,…,σN]T、响应R=[keff]T条件下，按上述抽样方法进行不确定度分析的计算模型完成由截面的不确定度对keff造成的不确定度的分析计算。

1.2计算流程及程序开发

根据上述基于抽样方法的不确定度分析模型，开发了反应堆物理计算不确定度分析程序UNICORN，计算流程如图1所示。

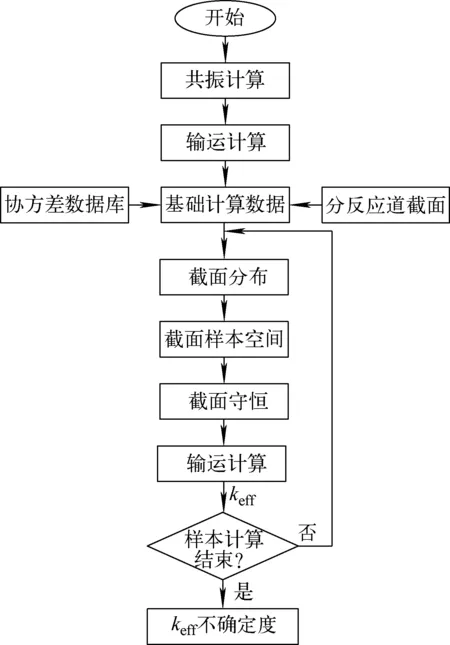
图1　UNICORN程序计算流程 Fig.1　Procedure for calculation of UNICORN code

UNICORN程序能计算(n,elas)、(n,inel)、(n,2n)、(n,α)、(n,p)、(n,γ)和(n,f)等分反应道截面σelas、σinel、σ2n、σα、σp、σγ和σf及平均裂变中子数ν的不确定度对反应堆物理计算结果造成的不确定度。计算所需的基础计算数据包括有效自屏截面、分反应道截面和多群协方差数据库。有效自屏截面由组件计算程序DRAGON经共振计算获得，包括输运计算涉及核素的总散射截面σs、总截面σt和共振核素的共振截面等。(n,inel)、(n,2n)、(n,α)和(n,p)等分反应道截面通过NJOY程序的输出文件获取，这些反应道是阈能高于共振能量的截面，不随稀释截面而变化，且在输出文件中给定的不同温度点的截面大小相同。因此，这些分反应道截面不随稀释截面和温度变化，可作为常数直接用于计算。多群协方差数据库采用NJOY程序基于ENDF/B-Ⅶ.1评价数据库制作产生，其中包含了(n,elas)、(n,inel)、(n,2n)、(n,α)、(n,p)、(n,γ)和(n,f)等分反应道截面及ν不同的能群之间的方差和协方差信息。

截面样本空间通过抽样的方法产生，样本空间包含多群协方差数据库中所有分反应道截面样本。由式(10)多群中子输运方程可知，输运计算所需的截面包括σf、σt和σs，其他的分反应道截面在输运计算中未直接使用。为将分反应道截面样本反映到输运计算所需的加和截面中，需对加和截面进行截面守恒处理[9]：

(12)

(13)

(14)

通过上述截面守恒公式，在对分反应道截面抽样过程中，保持加和截面的自洽守恒，用于后续的输运计算。

获取输运计算所需的加和截面后，采用DRAGON程序完成输运计算，提供由输入样本计算获得的keff，用于统计计算其不确定度。本文计算所需的有效自屏截面来自DRAGON程序的共振模块输出。

根据以上理论模型和计算流程，研发反应堆物理计算不确定度分析程序UNICORN，实现由分反应道截面的不确定度对输运计算的keff造成的不确定度的分析研究。

1.3协方差数据库

核数据源于实验测量和模型计算，不可避免地存在一定的偏差，即不确定度，用于描述核数据不确定度信息的协方差数据库保存在评价数据库数据中，协方差数据需制作成多群的形式使用[1]。本文通过NJOY程序，基于ENDF/B-Ⅶ.1评价数据库，研制用于反应堆物理计算的多群协方差数据库。输运计算采用69群WIMSD格式数据库，相应地，多群协方差数据库也研制成69群的格式。

2数值结果及验证

为验证UNICORN程序的正确性，采用UNICORN程序对UAM(uncertainty analysis in modeling)的计算基准题三哩岛(TMI)燃料棒的k∞的不确定度进行计算，并与文献结果对比。同时，为进一步验证UNICORN程序的正确性并研究不同来源的协方差数据库对k∞的不确定度计算的影响，对NECP实验室基准题RB31[10]的k∞进行不确定度分析计算，计算结果与TSUNAMI程序对比。

2.1TMI计算结果及分析

TMI燃料棒是典型的压水堆栅元，对其k∞的不确定度计算是UAM计算基准题[2]，国际上已给出相关的研究结果。表1列出了本文和文献[11]的对TMI燃料棒k∞不确定度引入较大的5种参数对的结果对比(表中的σc为俘获截面)，表中给出的是对应的参数对之间的协方差数据导致的k∞的相对不确定度。本文计算结果是在各分反应道截面服从正态分布，且计算样本数nS=100的计算条件下得到的。对于单个响应计算，根据Wilks最小样本限值理论[12]：响应以95%的置信度覆盖5%～95%的分布空间所需的最小样本数为93。本文计算采用100的样本数，计算结果的置信度高于95%。国际上采用抽样方法对反应堆物理计算进行不确定度分析时，未对计算样本的统计涨落进行评价。为提高样本计算结果的可信度，本文分别对样本数nS=100的20个不同的样本空间计算得到的k∞相对不确定度进行统计，给出其相对不确定度[13]，量化计算样本的统计涨落。

表1　TMI燃料棒 k ∞相对不确定度结果

表1中，本文的计算结果由两部分组成：相对不确定度计算结果的期望及其标准差。表1的结果表明，本文的计算结果与文献给出的计算结果符合很好，可证明本文开发的多群协方差数据库及不确定度分析程序UNICORN的正确性。对比表1发现，本文采用抽样方法与CASMO-4以及TSUNAMI采用微扰理论的计算结果之间存在一定的偏差，其原因主要包括两方面：抽样方法存在一定的统计涨落；微扰理论用于不确定度分析计算进行了一阶近似，而抽样方法不存在近似。CASMO-4与TSUNAMI程序对238U核素俘获截面的结果存在一定的偏差，文献[11]给出其原因在于TSUNAMI程序采用的ENDF/B-Ⅵ的截面数据相比CASMO-4采用的E60200数据库，238U的共振积分被低估了。

表2列出了多群协方差数据库中包含的所有分反应道截面及ν对TMI燃料棒k∞造成的相对不确定度的期望及其标准差的计算结果。其中，最大值和最小值分别表示采用以上介绍的20个不同计算样本空间计算得到的k∞相对不确定度的最大值和最小值，期望值表示对所有计算样本计算得到的相对不确定度进行统计的均值，标准差表示不同样本计算得到的k∞的相对不确定度的标准差，用于评价计算样本的统计涨落。

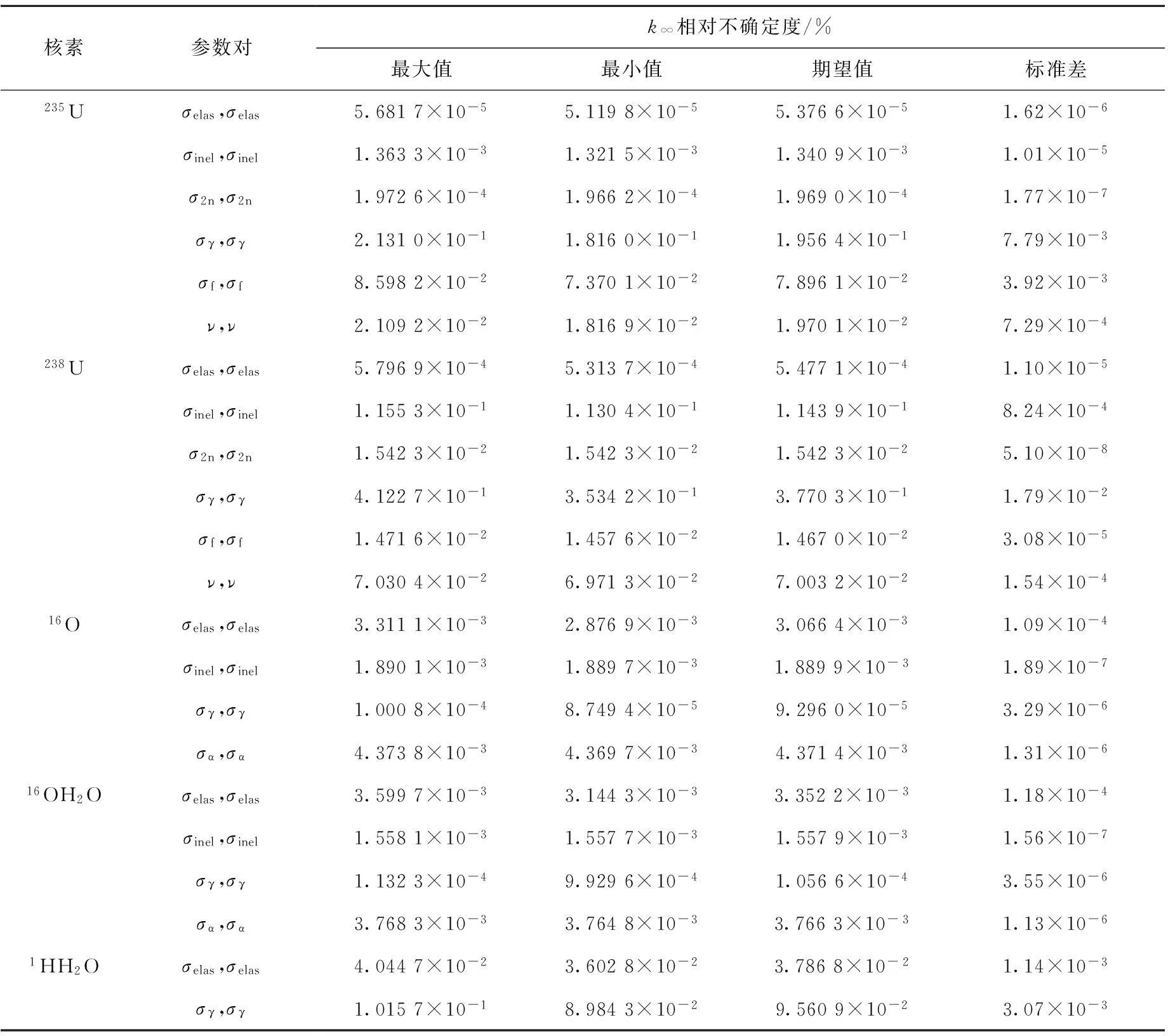
表2　分反应道截面及 ν对TMI燃料棒 k ∞相对不确定度计算结果

表2表明，在不同的计算样本空间条件下，本文计算得到的k∞相对不确定度存在5%以内的相对不确定度，这是对本文计算结果的统计涨落的量化。在计算样本数nS=100的计算条件下，根据Wilks最小样本限值理论，计算结果的置信度高于95%，统计学涨落在5%以内，本文的计算结果具有较高的可信度。

对比表2中计算结果可知，235U和238U对计算结果引入的不确定度较大。其中，238U的(n,γ)反应道造成的相对不确定度最大，在0.4%左右，这与国际现阶段的研究结果[1]相符。对比燃料中16O和慢化剂中16OH2O的计算结果可发现，阈能截面σinel和σα在燃料中较在慢化剂中对k∞造成的相对不确定度更大，这个结果符合物理本质：燃料中的中子具有较高的能量，而慢化剂中的中子能量较低，具有阈能的截面在燃料区的影响大于其在慢化剂中的影响。表2的计算结果表明，核数据的不确定度会对反应堆物理计算引入不可忽略的影响，需对其进行不确定度分析计算。

2.2RB31计算结果及分析

为增加对UNICORN程序的验证，并研究不同来源协方差数据库对不确定度分析结果的影响，UNICORN程序采用与TMI计算相同的20个nS=100的计算样本，对NECP实验室基准题RB31的k∞进行不确定度分析计算，计算结果与TSUNAMI程序结果进行对比，235U和238U对k∞造成的相对不确定度结果列于表3。

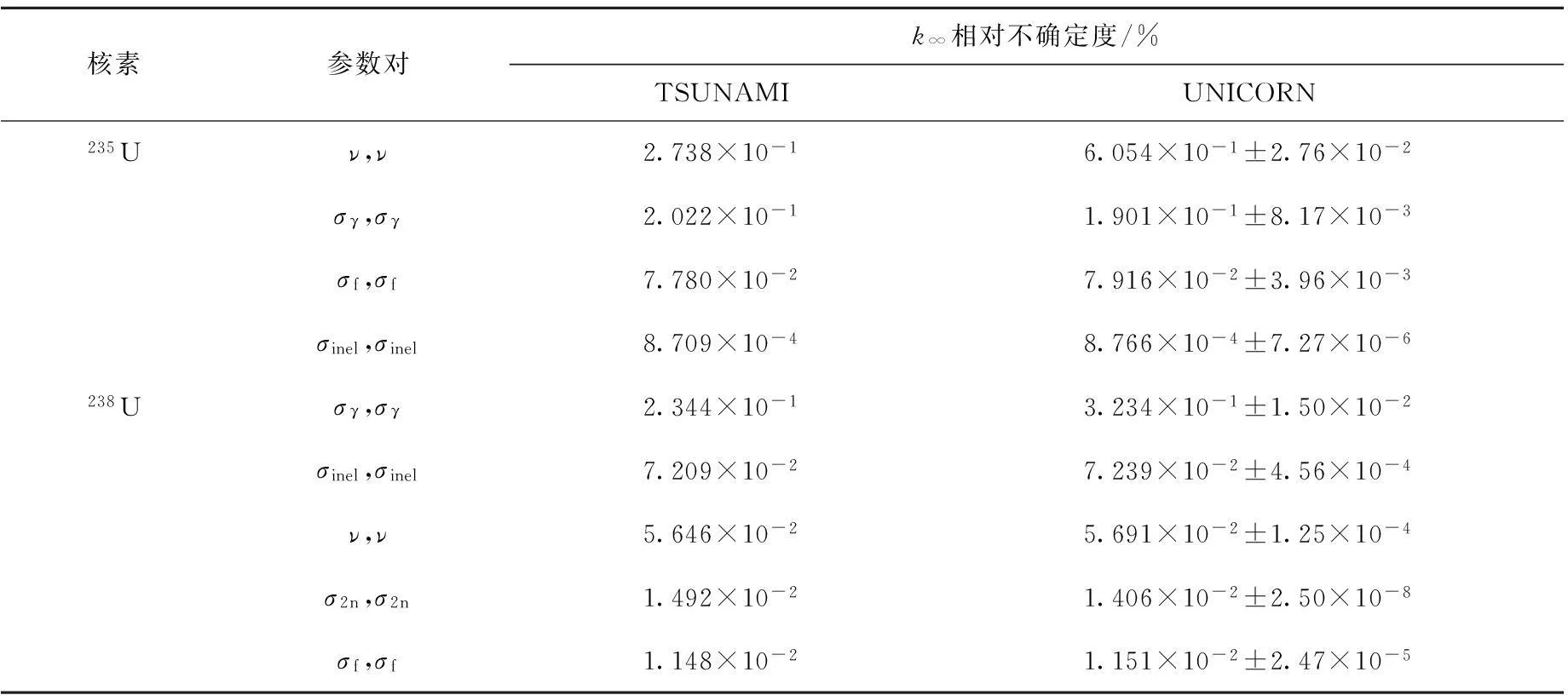
表3　 235U和 238U对RB31的 k ∞的相对不确定度

表3中UNICORN和TSUNAMI程序计算得到的235U和238U各反应道截面及ν对k∞造成的相对不确定度的结果对比表明，除235U核素的ν外，其他反应道截面的计算结果均吻合较好。造成这种差异的原因在于：TSUNAMI程序中，238U核素协方差数据源自ENDF/B-Ⅶ-p(ENDF/B-Ⅶ.1早期版本)评价数据库；235U核素的ν协方差源自JENDL-3.1评价数据库，其他截面协方差均源自ENDF/B-Ⅶ-p评价数据库[14]。UNICORN程序计算中采用的协方差数据库源自ENDF/B-Ⅶ.1评价数据库，与238U和235U各反应道截面的协方差数据库的来源一致。为对此原因进行验证，基于JENDL-3.1评价数据库，研制69群235U的ν协方差数据库，并用于RB31k∞的相对不确定度分析计算，计算结果列于表4。

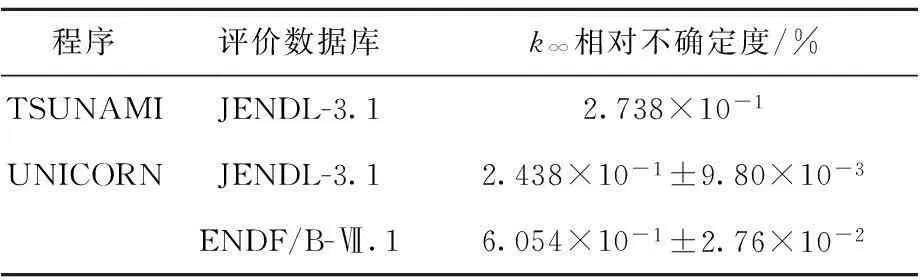
表4　 235U的 ν对RB31的 k ∞相对不确定度

表4的计算结果表明，UNICORN程序采用源自JENDL-3.1的协方差数据库的计算结果与相同协方差数据库来源的TSUNAMI程序的计算结果能很好吻合。因此，协方差数据库的来源不同，是导致UNICORN程序和TSUNAMI程序对235U核素的ν不确定度分析结果存在较大差异的原因。同时，表4也表明，协方差数据库的不同来源会对不确定度分析结果造成一定影响，采用不同的评价数据库计算得到的不确定度也不同。

3结论

本文基于抽样理论研究了用于反应堆物理计算的不确定度分析方法，开发了反应堆物理计算不确定度分析程序UNICORN。基于ENDF/B-Ⅶ.1数据库开发了多群协方差数据库。基于不确定度分析程序和多群协方差数据库，对TMI燃料棒和RB31的k∞进行不确定度分析计算，并量化计算结果的统计涨落。计算结果表明，本文开发的UNICORN程序是正确的，238U的(n,γ)反应道对TMI燃料棒的k∞造成的相对不确定度最大，约0.4%，且协方差数据库的不同来源会对不确定度分析结果造成一定的影响。

参考文献：

[1]WIESELQUIST W, VASILIEV A, FERROUKHI H. Nuclear data uncertainty propagation in a lattice physics code using stochastic sampling[R]. Tennessee, USA: American Nuclear Society, 2012.

[2]BALL R M. Uncertainty analysis in lattice reactor physics calculations[D]. Canada: McMaster University, 2012.

[3]WILLIAMS M, WIARDA D, SMITH H, et al. Development of a statistical sampling method for uncertainty analysis with SCALE[R]. Tennessee, USA: American Nuclear Society, 2012.

[4]ROCHMAN D, KONNG A J, MARCK S C V, et al. Nuclear data uncertainty propagation: Total Monte Carlo vs. covariances[J]. Journal of the Korean Physics Society, 2011, 59: 1 236-1 241.

[5]HELTON J C, JOHNSON J D, SALLABERRY C J, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis[J]. Reliability Engineering and System Safety, 2006, 91: 1 175-1 209.

[6]高惠璇. 应用多元统计分析[M]. 北京：北京大学出版社，2005.

[7]HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[R]. USA: Sandia National Laboratory, 2001.

[8]谢仲生, 邓力. 中子输运理论数值计算方法[M]. 西安：西北工业大学出版社，2005.

[9]IAEA. WIMS-D library updated[R]. Vienna: International Atomic Energy Agency, 2007.

[10]WU Hongchun, YANG Weiyan, QIN Yulong, et al. Benchmark problems and results for verifying resonance calculation methodologies[R]. Tennessee, USA: American Nuclear Society, 2012.

[11]PUSA M. Incorporating sensitivity and uncertainty analysis to a lattice physics code with application to CASMO-4[J]. Annals of Nuclear Energy, 2012, 40: 153-162.

[12]WILKS S S. Determination of sample sizes for setting tolerance limits[J]. Annals of Mathematical Statistics, 1941, 17: 208-215.

[13]ARCHER G E B, SALTELLI A, SOBOL I M, et al. Sensitivity measures, anova-like techniques and the use of bootstrap[J]. Journal of Statistical Computation and Simulation, 1997, 58(2): 99-120.

[14]WILLIAMS M L, WIARDA D, ARBANAS G, et al. Scale nuclear data covariance library[R]. US: ORNL, 2009.