直线超声电机驱动的精密运动平台位移分辨率

直线超声电机驱动的精密运动平台位移分辨率

王金鹏1，周宏平1，时运来2

(1.南京林业大学机械电子工程学院,南京210037；2.南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)

摘要：由于纳米级精度运动平台在电子隧道扫描显微镜、光刻机及精密医疗设备有广泛需求，传统驱动方式中大行程、高精度难以同时实现，而直线超声电机直接驱动的精密运动平台可望解决该问题。研究所建大行程直线超声电机系统位移分辨率影响因素，通过死区时间理论及启停实验曲线分析探索运动平台可能达到的最小步距；借助XL-80激光干涉仪，实验研究驱动波形、预压力及驱动电压对平台步距影响。结果显示，运动平台分辨率可达25 nm。

关键词：直线超声电机；平台；实验；位移分辨率；步距

中图分类号:TM356文献标志码：A

Displacement resolution of precision stage driven by linear ultrasonic motors

WANGJin-peng1,ZHOUHong-ping1,SHIYun-lai2(1. College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China; 2. State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)

Abstract:Nanometer-accuracy stage is widely needed in the scanning tunneling microscope (STM), lithography, precision medical equipments, and so on. In the traditional style of driving method, large stroke and high accuracy is as usual a pair of contradiction for precision stage. However, the precision stage driven by linear ultrasonic motor (LUSM) may reconcile the problem. For an established linear ultrasonic motors system, the influential factors to displacement resolution were studied. The possible minimum step of the stage was discussed in the light of the dead-time theory and the start-stop experimental curve. Then, under the help of XL-80 laser interferometer, the relationships between the micro-step distance of the stage and the driving factors, such as the driving waveform, pre-pressure and driving voltage, were studied respectively by experiments. The experimental results show that the displacement resolution is 25nm.

Key words:linear ultrasonic motor; stage; experiment; displacement resolution; step distance

精密运动平台广泛用于显微外科手术、高密度光存储器、探针扫描控制、电子隧道扫描显微镜等领域[1-2]。随科技的发展，纳米级定位精度运动平台尤其大行程多自由度精密运动平台需求量增大，其定位精度与驱动单元性能密切相关。精密致动技术可分为两类，即电磁式、非电磁式[3]。压电陶瓷致动属非电磁技术，具有响应快、结构简单、断电自锁、分辨率高等优点，是精密电子产品制造、超精密加工等设备驱动的重要选项。

超声电机作为压电作动器的一种[4-6]，具有速度快、推力/重量比大等特点[7-8]。与精度达纳米级、行程仅几十个微米的非共振式压电电机驱动精密微动台[9-10]不同[11]之处在于，超声电机驱动的精密运动平台定位精度可达微米级甚至纳米级同时，行程亦能达到几百毫米。朱煜等[12-13]为兼顾行程，对宏微结合精密运动平台进行研究，并试制出大行程、高精度运动平台，但整个设备较庞大，结构非常复杂，致其应用受限。

对精密运动平台位移分辨率、纳米级定位精度测试方法主要基于飞秒光频梳的精密位移测量技术[15]，用激光干涉仪[14]测量；在微小范围内的精密位移测量有电学方法，如电阻法、电容法、电感法、电涡流法等；显微镜测量方法，如高性能透射电子显微镜(TEM)、扫描探针显微镜(SPM)等[16]。但对大行程(几百mm)纳米级精度的位移测量，仅光栅尺及激光干涉仪能胜任，故本文用XL-80激光干涉仪研究精密运动平台的位移分辨率。通过理论与实验结合研究运动平台在不同驱动参数下的位移分辨率，并测定双足直线超声电机[17]驱动单自由度直线平台分辨率，为精确控制提供依据。

1运动平台微步距极小值

实践表明，运动平台位移分辨率会受驱动信号参数、预压力、摩擦副材料等影响，欲进一步提高运动平台的定位精度，则须全面研究各种驱动参数与平台位移分辨率的关系，寻找可提高位移分辨率的参数组合。

1.1微步距产生机理分析

驱动平台超声电机用两路相位差90°的数千赫兹信号进行驱动，测试运动平台位移分辨率时，电机采用间歇性脉冲串，每串信号含n1个完整的驱动周期，见图 1。图中为正弦信号，但用信号发生器结合功率放大器实验时，可改成方波、三角波、锯齿波等任意波形。与连续驱动的区别在于驱动信号在驱动n1个周期后会有一停顿间隔，间隔时间长短可据运动平台振荡不同进行调整。在n1个周期驱动信号作用下，电机驱动平台移动位移即为运动平台步距。若n1足够小，直到恰好可驱动平台运动形成稳定的可分辨位移即认为获得运动平台位移分辨率。由此可见，直线超声电机此时工作在启动过程与达到稳定状态前的中间状态。

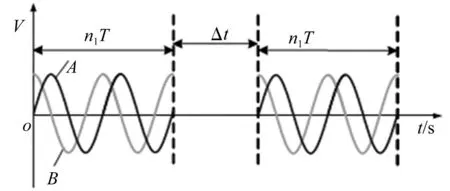
图1　步距实验驱动波形示意图 Fig.1 The driving waveform used in the experiments

1.2微步距理论预测值

由实验可得平台在连续信号驱动时的启停速度特性曲线，而采用脉冲串驱动时曲线必与此相似，二者示意图见图 2，由此可从理论上分析平台位移分辨率。测试分辨率实验中，平台未达到稳定的最大速度vsm时电机开始关闭过程，因预压力弹簧作用，电机定子与平台间静摩擦力开始阻碍平台继续运动，由平台速度曲线知，在ts0～ts1时间段平台作加速运动，ts1～ts2时间段作匀减速运动，在ts2时刻停止。ts0～ts2时间内平台走过的距离即微步距。

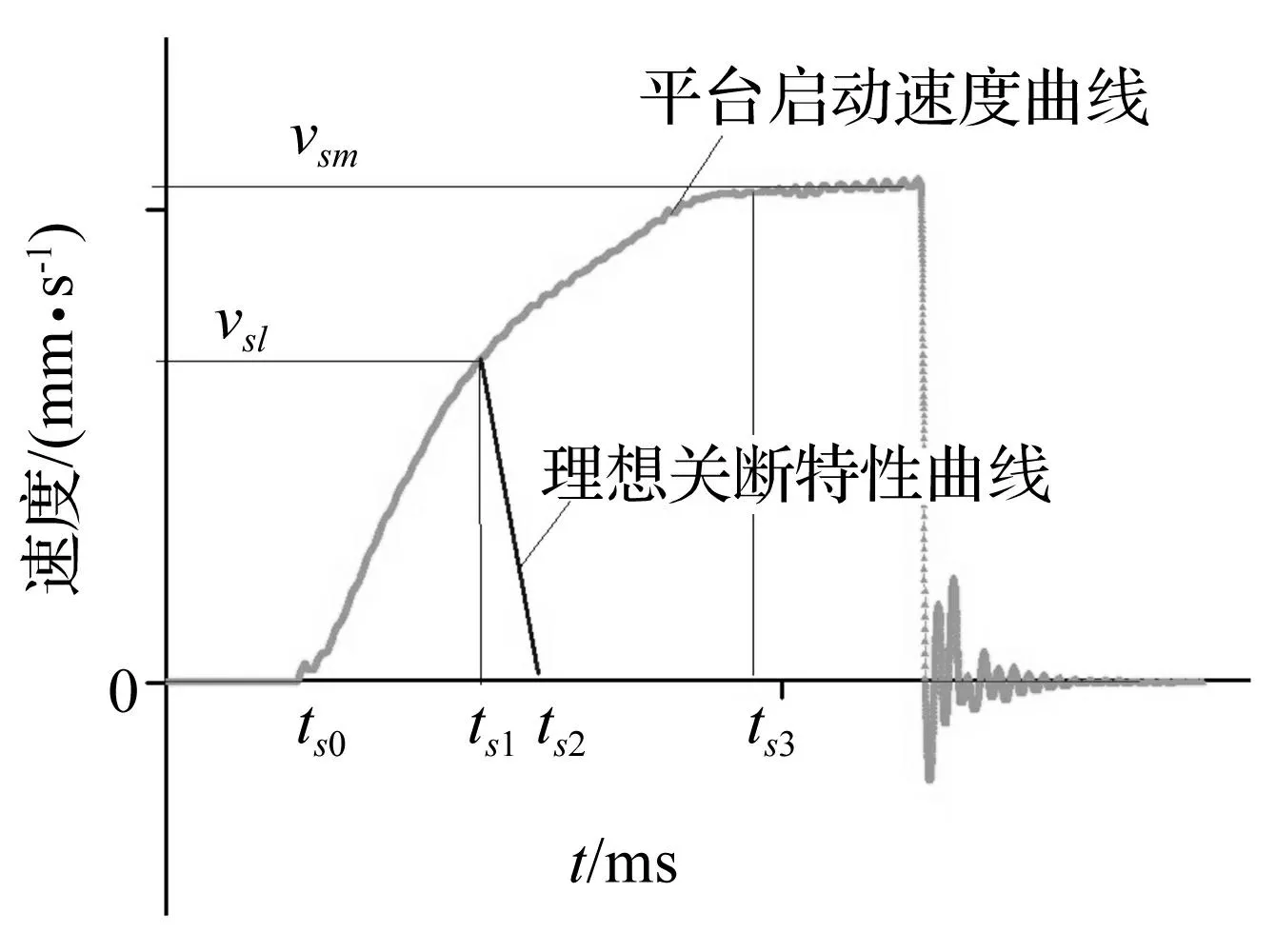
图2　运动平台启停特性曲线 Fig.2 Start-stop curve of stage

平台稳定的最大速度vsm与启动时间ts3可通过实验获得。近似得平台在ts1时刻的速度vsl为

(1)

因此，在(ts0～ts1)时间段内平台走过的距离可近似表示为

(2)

在(ts1～ts2)时间段内平台走过的距离为

(3)

在ts0～ts2时间段内平台位移与单元驱动时间及平台连续工作时所能达到的最大速度关系为

(4)

式中：ts1-ts0为平台克服静摩擦力开始运动的时间n1T，T为电机驱动信号周期。

为达到测试位移分辨率目的，可减少驱动信号周期个数n1，或同时调整驱动信号频率1/T。显然，要保证能驱动平台产生位移，驱动信号周期个数n1不能为零，即平台驱动时间存在极小值，设其为ts0，则0～ts0为平台的死区时间，即从平台驱动单元开始工作到平台运动至检测仪能分辨的最小位移所经一瞬间。据上式，在已知平台最大速度、启动死区时间情况下，即可预测平台位移分辨率。

2实验系统搭建

实验系统及示意图见图3。任意信号发生器AFG3022产生所需信号，经HFVP-83A功率放大器后施加于定子，用XL-80激光干涉仪测试实验滑台微小位移。激光干涉仪标称稳定精度为±1 nm，实验室保持恒温、洁净，地基经隔振处理，选室外干扰较小的21∶00后进行。实验前，归零的显示器界面纳米位数字仅有缓慢变化，即10 s内变化不超过5 nm，因每次实验持时仅几秒，故忽略其影响。实验中用信号发生器监视信号放大前后变化，以保证施加于定子波形的准确性。定子预压力设定过程中用LC1015压力传感器及显示器控制数值大小。运动平台置于气浮实验台上，将信号发生器及带散热风扇的功放置于距离约1 m的另个大理石气浮平台上，尽可能避免环境因素对测量精度影响。实验用部分信号放大后波形见图3(c)。

图3　微步距实验测试系统及示意图 Fig.3 Micro-step test system and its sketch map

3不同参数的信号对步距影响

3.1不同信号波形对微步距影响

研究不同波形驱动信号对直线超声电机步距影响有利于找到提高运动平台位移分辨率的参数组合。实验中经功率放大器后施加于电机定子的方波信号未转成近似正弦波形，仍近似为方波。而用信号发生器直接产生正弦波，经功率放大器施加于电机定子，却在示波器上显示为正弦波形。实验中亦用过三角波、锯齿波等波形信号。设相邻两组信号间隔为100 ms，目的为使平台每走一步产生的振荡得到充分衰减，能清晰分辨出每步位移。振荡产生的原因可从两方面解释，

即①机械响应本身原因，与定子及滑台构成系统的阻尼有关；②从电学角度解释，因压电陶瓷呈现容性，能与驱动器的感性元件构成振荡回路。通过设置可使平台恰好能产生连续稳定的微小位移(微步距)，以达到测定电机位移分辨率目的。

不同驱动波形实验结果见图4。由图4可知，在50 kHz附近时各种驱动波形产生的步距均较大，说明此时超声电机能量转换效率较高；相同条件下仅方波信号驱动时，能在10～70 kHz范围内稳定驱动滑台。分析认为，与其它驱动信号相比，方波信号作用下定子对动子的冲击更强，使二者更易突破静摩擦力起主导作用的相对静止状态。故实验信号均用方波信号。

在20 kHz时方波及锯齿波均出现极小值，而正弦波及三角波在频率降到20 kHz时几乎无法形成稳定的步进运动，可能是后者在驱动足推程、回程中因驱动波形对称而导致前进、后退位移基本相等；方波与锯齿波出现极小值也因定子推动动子形成的前进、后退位移差达到最小。若频率继续减小，则起主导作用的将由高频谐振驱动模式转换为静变形驱动模式。在频率超过70 kHz并继续增加时，因偏离直线超声电机定子设计的共振频率点(50 kHz)，故在其它条件相同情况下，图4中曲线呈单调下降趋势，直至趋近于零。

3.2预压力对步距影响

采用2个周期频率为50 kHz方波信号，放大后电压为300 Vpp(峰峰值)；测试预压力对步距影响，结果见图5。由图5可知，预压力从20 N增加到70 N时步距随预压力增大而增加，但预压力继续增加时步距有减小趋势；当预压力小于20 N时步距又有所增加，原因为随预压力进一步减小，惯性导致滑台滑动位移大幅增加。预压力为零时定子与滑台脱离，滑台无法产生运动，步距也会变零；若预压力无限增大，定子产生的力无法客服定子、动子间摩擦力，无法使定子/动子脱离，滑台将无法产生相对运动。

图4 直线超声电机驱动波形与运动平台步距关系Fig.4RelationshipbetweendrivingwaveformofLUSMandstepdistanceofstage图5 直线超声电机预压力与运动平台步距关系Fig.5Relationshipbetweenpre-pressureofLUSMandstepdistanceofstage图6 直线超声电机驱动电压与运动平台步距关系Fig.6RelationshipbetweendrivingvoltageofLUSMandstepdistanceofstage

3.3驱动电压与步距关系

驱动电压大小直接影响直线超声电机驱动足端部振幅，对非共振状态下驱动电压对步距影响进行研究非常必要。驱动信号为50 kHz方波，4个信号周期一组，组与组之间停顿100 ms，预压力为40 N时实验结果见图6。由图6看出，在150～450 Vpp之间步距随电压升高而增大，驱动电压小于100 Vpp时定子无法驱动滑台产生稳定的步进运动，原因为定子振幅太小，在极短工作时间内无法积累足够能量有效克服定子动子间静力约束，定子/动子无法脱离并产生相对运动。

4位移分辨率测定实验

实验平台与激光干涉仪置于气浮平台上，稳压电源、信号发生器、功放及示波器等与其隔离，运动平台位移分辨率实验结果见图7。图7(a)显示，在100 kHz的1个方波信号、30 N预压力、驱动电压350 Vpp情况下位移分辨率达到25 nm。(100+1/ 100)ms中的100 ms为信号发生器发送1个周期信号后停顿100 ms不发送信号给功放，1/100 ms为所用100 kHz信号一个周期持时。每步间100 ms停顿，为使平台每走一步的振荡充分衰减以能分辨出每步位移，同时又不使平台停止时间太长，便于在较短时间段内测出较多周期，尽可能反映出更多关于定位平台步进运动信息。此振荡由动子机械振动引起，属欠阻尼振动；第二次重复测量所得分辨率为29 nm(图7(b))；调整信号频率为400 kHz、预压力60 N后，所测结果见图7(c)、(d)，运动平台位移分辨率分别为24 nm及21 nm。其中图7(c)为连续步进20步情况。以上4结果均在不同测试条件下获得，可见此平台实现微步距运动条件不唯一，将数据求平均值获得直线超声电机驱动运动平台位移分辨率为24.75 nm，即25 nm。

图7　直线超声电机驱动运动平台位移分辨率 Fig.7 Displacement resolution of the stage driving by LUSM

5结论

为探究超声电机驱动直线运动平台步进时的步距极值，测试各种驱动参数对运动平台步距影响。结果表明，在50 kHz附近，各种驱动波形驱动平台步距均较大，离该频率越远步距越小，不同驱动信号驱动效果差异明显。方波信号能覆盖较宽的频率范围(10～70 kHz)。预压力超过20N时步距随预压力增加先增加后减小；驱动电压超过100 Vpp时步距随电压升高而增加。

参考文献

[1]王立鼎,褚金奎,刘冲,等. 中国微纳制造研究进展[J]. 机械工程学报,2008(11): 2-12.

WANG Li-ding, CHU Jin-kui, LIU Chong, et al. New developments on micro-nano manufacture technology in China[J]. Chinese Journal of Mechanical Engineering, 2008(11):2-12.

[2]王金鹏,金家楣,赵淳生. 用于精密定位平台的直线超声电机的异步并联[J]. 光学精密工程, 2012, 19(11): 2693-2702.

WANG Jin-peng, JIN Jia-mei, ZHAO Chun-sheng. Asynchronous bundling of linear ultrasonic motor for precision positioning stage[J]. Optics and Precision Engineering,2012, 19(11):2693-2702.

[3]时运来. 新型直线超声电机的研究及其在运动平台中的应用[D]. 南京: 南京航空航天大学, 2011.

[4]许海,赵淳生. 双足型直线超声电机的结构及实验[J]. 振动与冲击,2007,26(6):100-102.

XU Hai, ZHAO Chun-sheng. Structure of double feet liner ultrasonic motor and its modal experiment[J]. Journal of Vibration and Shock,2007,26(6):100-102.

[5]陈乾伟,黄卫清. 塔形超声电机的突变结构弹性支撑[J]. 振动与冲击,2012,31(24):74-81.

CHEN Qian-wei, HUANG Wei-qing. Tower-shaped ultrasonic motor’s elastic support with abrupt changing configuration[J]. Journal of Vibration and Shock, 2012,31(24): 74-81.

[6]张露,李朝东. 背衬封装对卧板式直线超声电机输出推力影响[J]. 振动与冲击,2013,32(11):137-140.

ZHANG Lu, LI Chao-dong. Effect of back packaging on output thrust of a board-type horizontal linear ultrasonic motor[J]. Journal of Vibration and Shock,2013,32(11): 137-140.

[7]贺红林,武冬梅,何文丛,等. H-结构薄板纵弯复合模态驱动的压电直线电机[J]. 振动与冲击,2013,32(5): 1-5.

HE Hong-lin, WU Dong-mei, HE Wen-cong, et al. Ultrasonic linear motor driven by the longitudinal and bending vibration modes of an H-shaped vibrator[J]. Journal of Vibration and Shock,2013,32(5): 1-5.

[8]赵淳生. 超声电机技术与应用[M]. 北京: 科学出版社, 2007.

[9]陈立国,张洋,陈涛,等. 多目标拓扑优化设计在纳米定位平台中的应用[J]. 压电与声光,2011,33(2): 228-231.

CHEN Li-guo,ZHANG Yang, CHEN Tao, et al. Application of multi-objective topology optimization design on the nano-positioning stage[J]. Piezoelectrics and Acoustooptics, 2011,33(2): 228-231.

[10]刘国华,李亮玉. 压电驱动三维超微定位平台的性能研究[J]. 压电与声光,2007(3): 289-291.

LIU Guo-hua, LI Liang-yu. Study on theperformance of 3D ultra-micropositioning system with PZT[J]. Piezoelectrics and Acoustooptics,2007(3):289-291.

[11]Npoint. Piezo stages and nanopositioning systems[Z]. 2012: X25A.

[12]朱煜,尹文生，段广洪. 光刻机超精密工件台研究[J]. 电子工业专用设备,2004, 33(2):25-27.

ZHU Yu, YIN Wen-sheng, DUAN Guang-hong. Research onultra-precision stages of lithography[J]. Equipment for Electronic Products Manufacturing, 2004, 33(2):25-27.

[13]贾松涛,朱煜,杨开明,等. 双边驱动精密运动台振动特性研究[J]. 机械科学与技术,2009(5): 582-586.

JIA Song-tao, ZHU Yu, YANG Kai-ming, et al. Investigationof the vibration characteristic of a dual-drive precision stage[J]. Mechanical Science and Technology for Aerospace Engineering,2009(5): 582-586.

[14]刘泊,郭建英,孙永全. 压电陶瓷微位移驱动器建模与控制[J]. 光学精密工程, 2013(6): 1503-1509.

LIU Bo, GUO Jin-ying, SUN Yong-quan. Modeling and control for PZT micro-displacementactuator[J]. Optics and Precision Engineering, 2013(6): 1503-1509.

[15]朱敏昊,吴学健,尉昊赟,等. 基于飞秒光频梳的压电陶瓷闭环位移控制系统[J]. 物理学报,2013(7): 117-122.

ZHU Min-hao, WU Xue-jian, YU Hao-yun, et al. Closed-loop displacement control system for piezoelectric transducer based on optical frequency comb[J]. Acta Physica Sinica,2013(7): 117-122.

[16]段小艳,任冬梅. 激光干涉法微位移测量技术综述[J]. 计测技术,2012(6): 1-5.

DUAN Xiao-yan, REN Dong-mei.Review ofhigh-resolution measuring method of displacement using laser interferometer[J]. Metrology & Measurement Technology, 2012(6): 1-5.

[17]李玉宝. 新型直线型超声电机及其应用的研究[D]. 南京: 南京航空航天大学, 2009.