浮式平台立柱截面倒角半径对流力的影响
2016-01-10徐善辉杜庆贵尹宝瑞庄宏昌王程临
徐善辉,杜庆贵,尹宝瑞,庄宏昌,王程临
[1. 海洋石油工程(青岛)有限公司,青岛 266520;2. 中海油研究总院,北京 100028]
浮式平台立柱截面倒角半径对流力的影响
徐善辉1,杜庆贵2,尹宝瑞1,庄宏昌1,王程临1
[1. 海洋石油工程(青岛)有限公司,青岛 266520;2. 中海油研究总院,北京 100028]
浮式平台是深海油气资源开发的重要装备。在浮式平台作业过程中,流力对平台的定位有直接影响,是平台设计时需要考虑的重要因素。当平台设计方案确定后,立柱的主尺度将不能改变,其流力将取决于截面倒角。采用FLUENT软件对不同截面倒角立柱的流力进行了计算。结果表明,立柱倒角对拖航阻力有明显影响,当立柱截面倒角大于2 m时,流力可减少50%以上。研究结果可为浮式平台船型设计提供参考。
浮式平台;立柱;流力;FLUENT软件
0 引 言
浮式海洋平台是海洋油气开发的重要装备。常见的浮式平台包括钻井作业类平台和生产服务类平台,前者包括半潜式钻井平台、钻井船、半潜式修井平台等,后者包括半潜式生产平台、张力腿平台(TLP)、单立柱平台(SPAR)、浮式生产储卸油装置(FPSO)等。半潜式钻井平台、半潜式生产平台和TLP在上述装备中占比较大。这些平台船体结构主要可以分为三大部分:浮箱、立柱和上部模块。在作业工况下,浮箱和部分立柱浸没在水中,由于海流的作用,此部分会产生较大的流力。
以半潜式钻井平台为例[1]。在生存工况迎流时,立柱的流力贡献占总流力的1/3以上;在作业工况迎流时,立柱的流力贡献约占总流力的40%。由此,对平台立柱进行流力优化可降低在位工况下的流力。立柱的主尺度(长、宽)和截面形状对立柱的阻力都构成重要影响。但是,平台设计方案确定后,立柱的主尺度将不能随意改变,因此,流力优化研究可以重点关注立柱的横截面形状。
常见浮式平台立柱的截面形式有两种:圆形,如Sovereign Explorer号半潜式钻井平台和Brutus TLP;正方形导圆角形,如HYSY981半潜式钻井平台和Blind Faith半潜式生产平台。不同截面的关键区别在于截面倒角的大小。
本文采用FLUENT软件对某浮式平台的立柱取不同截面倒角计算其流力值[2-3],以期获得立柱截面倒角半径对立柱流力的影响规律,并获得立柱截面倒角半径的最佳取值范围。
1 基本公式及理论
研究采用FLUENT软件k-ε二维湍流模型求解半潜式钻井平台立柱截面绕流问题。压力速度的耦合方式采用PSIO算法,压力插值选择体积力加权积分,时间项采用二阶全隐式积分[4]。
结构流力与其几何形状、航速、水的运动黏性系数、水的质量密度和重力加速度等相关,因此必须探讨力与这些物理量的函数关系。引入无量纲数雷诺数Re对立柱的运动状态进行界定。
雷诺数表达公式为

,
(1)
式中:V为流场特征速度;L为特征长度;υ为流体的动力黏度。
计算时,可以得到两个力:沿流向的流阻力(拖曳力)Fd和垂直于流场的横向力Fl。为了便于比较,本文对流力系数和横向力系数进行研究。研究时,分析拖曳力系数Cd的大小和横向力系数Cl幅值大小随截面倒角半径的变化规律。拖曳力系数和横向力系数的表达式如下:
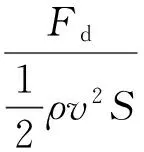
(2)

,
(3)
式中:Fd为作用于结构上的拖曳力;Fl为作用于柱体上的横向力;ρ为流场流体中密度;v为流场速度;S为结构的侧面积,S=lc·L(lc为结构截面周长,L为结构长度)。本文计算得到的流力皆为单位长度的力(L=1 m)。
2 水动力模型
参考某半潜式钻井平台结构图纸建立流域模型。
流域长1 200 m,宽500 m,立柱截面中心离入口300 m,立柱截面尺寸17.4 m×17.4 m,截面倒角半径R=0,1,…,8,8.7 m。流域及边界模型如图1所示。海水密度为ρ=1 003.25 kg/m3,水流速度为v=2 m/s。
边界条件设定如下。
左边界面(velocity_ inlet):速度入口边界条件,速度为 的流体从此边界均匀流入。
右边界面(outflow):自由出流边界条件,流体从此边界自由流出。
上边界面(top):对称边界条件,此边界上垂直流向分量为零。
下边界面(bottom):对称边界条件,此边界上垂直流向分量为零。
立柱轮廓线(pontoon):壁面边界条件,流体从壁面无滑移绕过。

图1 流域计算模型Fig.1 Model of the fluid domain
划分网格时采用总体流域网格局部加密技术,取坐标原点为中心120 m×120 m区域划分三角形网格,该区域外全采用四边形网格。流域网格图及立柱局部网格图如图2所示。

图2 流域网格模型Fig.2 Mesh model of the fluid domain
建立模型时,在截面附近区域,网格总数和形状尽量保持一致以提高对比精度。不同倒角半径时立柱模型数据如表1所示。
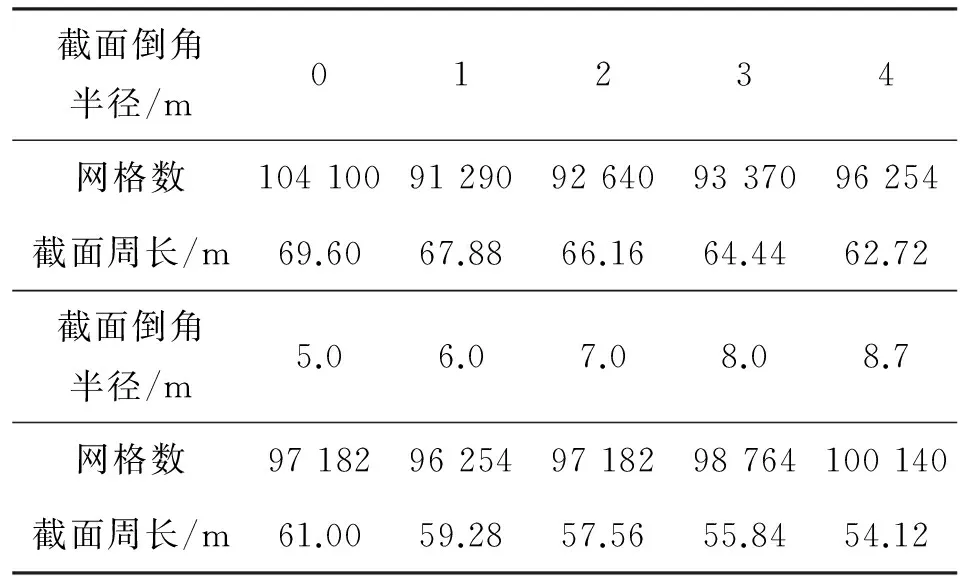
表1 不同倒角半径时立柱截面模型的网格数及截面周长
时间步长取0.01 s,计算稳定后调大至0.02 s。
3 计算结果
在t=500 s时,几个典型倒角半径下的涡量场及压力场分布云图如图3~5所示。
不同倒角半径时拖曳力系数和拖曳力如表2所示。表中拖曳力结果根据表1中截面周长和对应的拖曳力系数由式(2)计算而得。
不同倒角时横向力系数和横向力幅如表3所示。表中横向力幅值结果根据表1中截面周长和对应的横向力系数由式(3)计算而得。
不同倒角半径时,立柱的泄涡周期如表4所示。
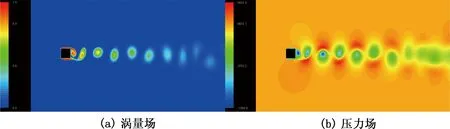
图3 倒角半径1 m时涡量场和压力场分布云图Fig.3 Contour of vortex and pressure around the column with a fillet radius of 1 m

图4 倒角半径5 m时涡量场和压力场分布云图Fig.4 Contour of vortex and pressure around the column with a fillet radius of 5 m
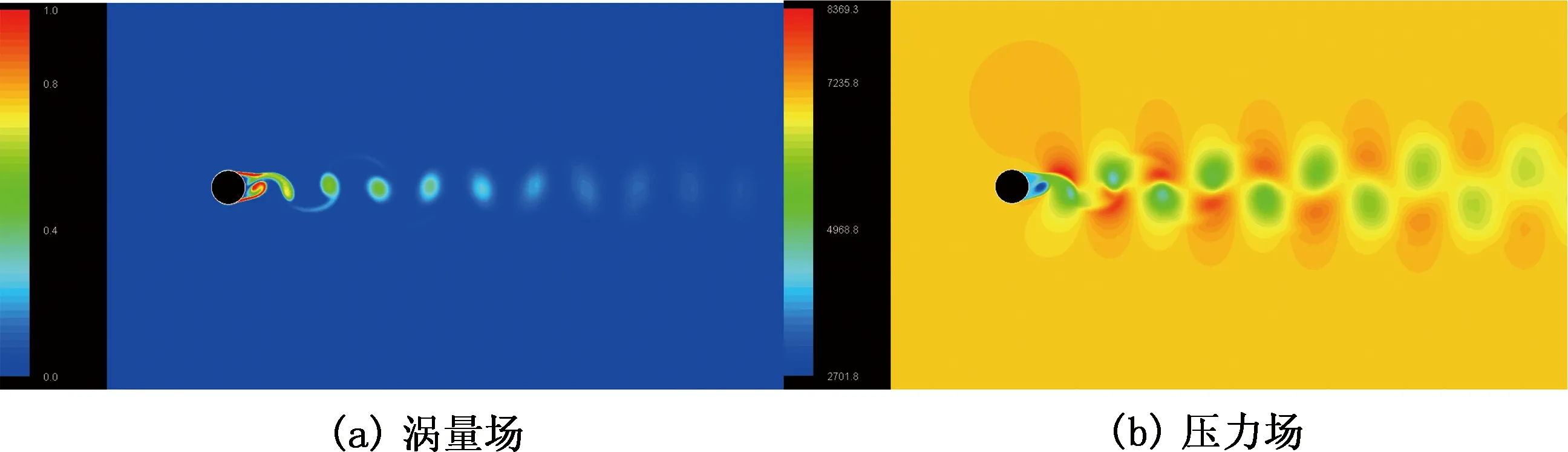
图5 倒角半径8.7 m时涡量场分布图和压力场分布云图Fig.5 Contour of vortex and pressure around the column with a fillet radius of 8.7 m

截面倒角半径/m01234流阻力系数Cd0.640.480.360.300.27流阻力/(N·m-1)89377.564695.647922.838531.133601.3截面倒角半径(m)56788.7流阻力系数Cd0.230.140.120.120.13流阻力/(N·m-1)28151.216176.613512.813109.014225.5
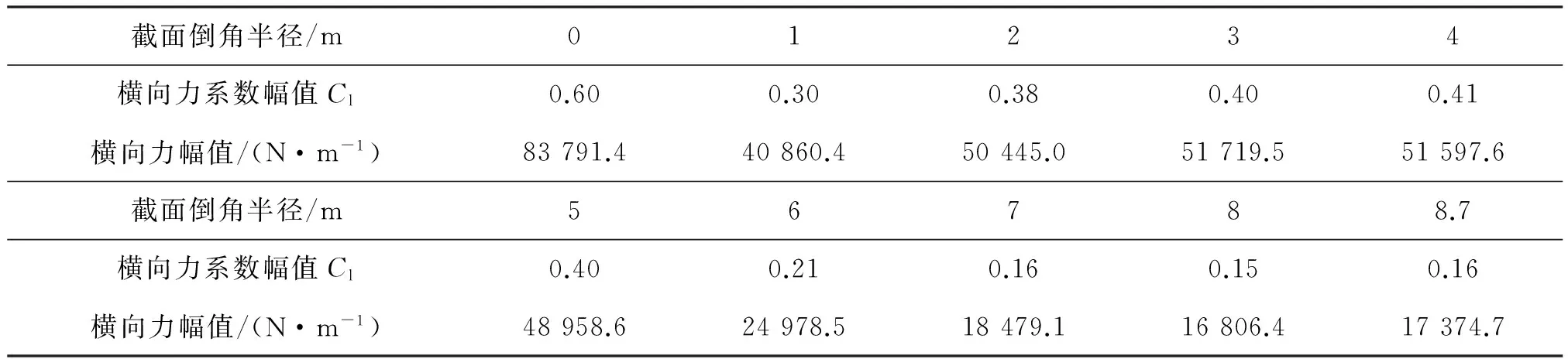
表3 不同倒角半径时的横向力及横向力系数

表4 不同倒角半径时的泄涡周期
4 结果分析
立柱绕流属于典型的钝体绕流,立柱的拖曳力和横向力与雷诺数密切相关。由式(1)可得,计算工况下雷诺数大于107,属于过临界区[5-6]。对于均匀来流,立柱截面下游会有涡泄出,并且涡的泄放呈现很强的周期性,横向力变化非常剧烈。
由图3~5可以看出,对于不同的倒角立柱,下游皆有均匀涡泄放,这与理论是一致的,并且不同倒角时,压力场和涡量场分布有一定的区别:倒角半径越大,涡量场和速度场变化越柔和。
由表2数据可得拖曳力及拖曳力系数随倒角变化曲线,如图6所示。
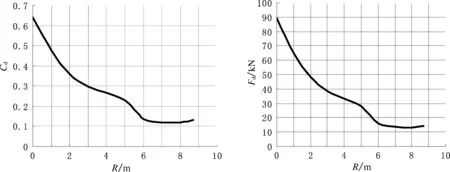
图6 拖曳力及拖曳力系数随倒角半径变化曲线Fig.6 Curves of the drag force and frag force coefficient versus fillet radius
由图6可以看出,倒角半径越大,立柱的拖曳力Fd越小,特别是R<3 m时,随着倒角半径变小,Fd急剧下降;当R>6 m时,随着倒角半径的变化,Fd变化非常缓慢。因此立柱截面倒角半径取在R>3 m便可大幅减小流阻力,此时Fd比方形立柱对应值小60%以上,并且在3 m
由表3数据可得横向力幅值及横向力系数随倒角半径变化曲线,如图7所示。分析可得,在倒角半径R<2 m时,横向力幅值Fl随倒角半径变化非常剧烈,特别是R=1 m时,出现了明显的拐点,这是由于不做倒角时壁面尖锐,涡的生成和泄放比较剧烈,做倒角后壁面广顺,壁面流特性显著变化;在倒角半径2 m
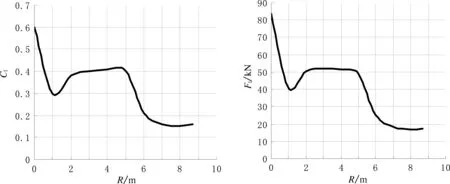
图7 横向力幅值及横向力系数随倒角半径变化曲线Fig.7 Curves of the lateral force and lateral force coefficient versus fillet radius
由表4数据可得泄涡周期随倒角半径变化曲线,如图8所示。

图8 泄涡周期随倒角变化曲线Fig.8 Curve of the shed vortex period versus fillet radius
在倒角半径R<4 m时,泄涡周期较大,随着倒角半径变大,泄涡周期变化不大;在倒角半径4 m
5 结 语
立柱截面倒角半径的选取需要考虑多种因素,要综合流力大小、泄涡周期、结构设计、建造可实现性等多重因素的影响。从立柱的流力和泄涡周期角度考虑,给出以下两点建议:方形截面立柱截面倒角半径越大,流力越小,但是到达一定程度后流力变化平缓;立柱倒角半径建议取值范围为2 m [1] 杜庆贵, 冯玮, 晏绍枝, 等. 半潜式钻井平台拖航阻力数值分析[J]. 石油矿场机械, 2012, 41(9): 23. [2] 杜庆贵, 冯玮, 晏绍枝, 等. 深水半潜式钻井平台横撑间距对拖航阻力的影响分析[J]. 中国海上油气, 2012, 24(4) : 71. [3] 杜庆贵, 冯玮, 粟京, 等. 半潜式钻井平台横撑截面形状的优化[J]. 舰船科学技术, 2012, 34(9) : 84. [4] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004: 121-122. [5] 刘应中, 缪国平. 高等流体力学[M]. 上海: 上海交通大学出版社, 2002: 237-239. [6] Faltinsen O M. Sea loads on ships and offshore structures [M]. Cambridge: Cambridge University Press, 1990: 173-222. [7] Pan Z, Cui W, Miao Q. A prediction model for vortex Induced vibration of slender marine riser [J]. Journal of Ship Mechanics, 2006, 10(3): 42. StudyontheCurrentForceontheColumnswithDifferentFilletRadiiofaFloatingPlatform XU Shan-hui1, DU Qing-gui2, YIN Bao-rui1, ZHUANG Hong-chang1, WANG Cheng-lin1 (1.Offshore Oil Engineering Co., Ltd., Qingdao, Shandong 266520, China;2.CNOOC Research Institute, Beijing 100028, China) Floating platform plays an important role in the development of deepwater oil resources. The current force acting on the floating platform is usually considered to be a critical factor for platform design. Once the design plan is finalized, the principal dimension of the column is fixed, and the current force will be mainly affected by the cross sections. The FLUENT software is used here to compute the force of the columns with cross sections of different fillet radii in a uniform viscous flow. According to the computation, the current force of the column with a fillet radius more than 2 m will be reduced by more than 50%. The research results may provide good reference to the design of a new platform. floating platform; column; current force; FLUENT software 2016-02-25 徐善辉(1985—),男,本科,工程师,主要从事海洋平台设计与建造方面的研究。 P751 A 2095-7297(2016)02-0111-05
