M矩阵最小特征值的新界

M矩阵最小特征值的新界

李艳艳，蒋建新

(文山学院数学学院，云南文山663000)

[摘要]给出了M矩阵A°B-1的最小特征值τ(A°B-1)的新界，这个新界一定情况下提高了两个经典的估计式，并且这也使估计τ(A°B-1)的界时的选择更加丰富.

[关键词]M矩阵；最小特征值；Hadamard积；界[收稿日期]2015-08-01

[基金项目]云南省教育厅科学研究项目(项目编号：2013Y585)，文山学院重点学科数学建设项目(项目编号：12WSXK01).

[作者简介]李艳艳(1982-)，女，甘肃庆阳人，文山学院数学学院讲师，硕士，主要从事矩阵理论及其应用研究.

[中图分类号]O151.21 [文献标识码]A

0预备知识

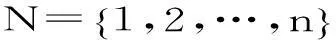
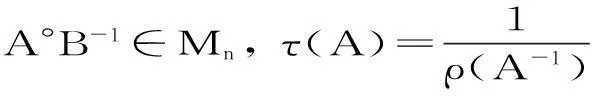
1主要定理

定理1设A，B是非奇异的M矩阵，B-1=(βij) ，则

证明：设C=A°B-1,由于A是M矩阵，B-1是非负矩阵，所以aii≥τ(A), ρ(B-1)≥bii.下面分两种情况来证明:

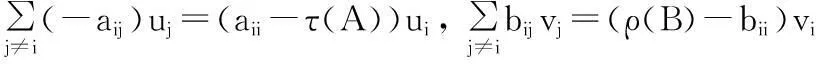
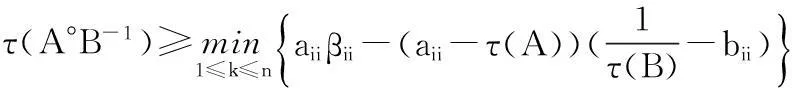
2. 若C可约，不失一般性，假设C有如下的块上三角形式

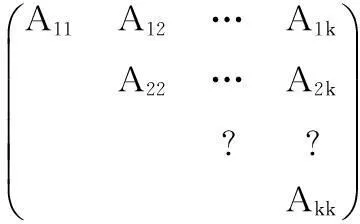
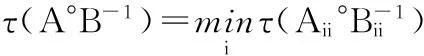
2数值算例

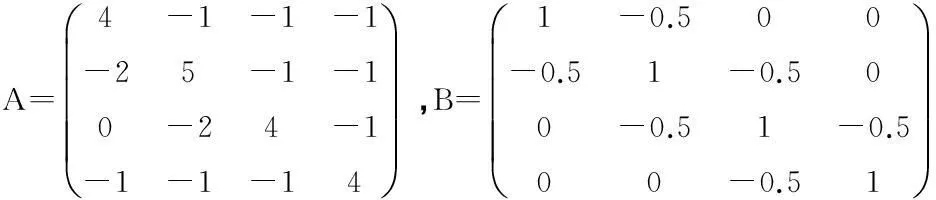
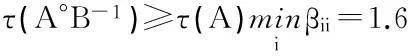
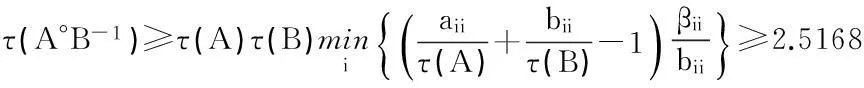
此例说明本文给的估计式一定情况下提高了现有的结果.这也使得估计τ(A°B-1)的界时的选择更加多样化.

参考文献

[1]李艳艳.严格对角占优M矩阵最小特征值的新界[J].沈阳大学学报，2015,27(3)：255-258.

[2]Chaoqian L,Yaotang LI,Ruijuan Z.New inequalities for the minimum eigenvalue of M-matrices[J]. Linear and Multilinear Algebra, 2013,61(9):1267-1279.

[3]Horn R A, Johnson C R. Topics in Matrix Analysis[M].New York:Cambridge University Press, 1991.

[4]Sheng C. A Lower bound for the minimum eigenvalue of the Hadamard product of matrix[J]. Linear Algebra Appl,2004(378):159-166.

[5]Rong H. Some inequalities for the Hadamard product and the Fan product of matrices[J].Linear Algebra and its Applications,2008,428:1551-1559.

[6]陈现平,王文省.两个矩阵同时对角化的条件[J].枣庄学院学报,2005,22(2):11-13.

[7]孔庆兰.分块矩阵的应用[J].枣庄学院学报,2006,23(3):34-36.

[8]李玲玲,李华,许伟涛.M矩阵最小特征值的新界值估计[J].河南大学学报(自然科学版)，2015,45(2):134-138.

[9]赵建兴. M-矩阵最小特征值估计及其相关问题研究[D].云南大学,2014.

[责任编辑：房永磊]