具有充分下降性的修正类Wei-Yao-Liu共轭梯度法

具有充分下降性的修正类Wei-Yao-Liu共轭梯度法

孙敏

(枣庄学院数学与统计学院，山东枣庄277160)

[摘要]基于最近的一些共轭梯度法的设计思想，本文提出了一类修正的Wei-Yao-Liu共轭梯度法.该方法的优点是每步迭代都可以产生充分下降方向，并且这个性质不依赖于线性搜索.在一类Armijo线性搜索下，该方法具有全局收敛性.最后的数值试验表明了新方法的有效性.

[关键词]Wei-Yao-Liu共轭梯度法;充分下降性;全局收敛性[收稿日期]2015-08-10

[作者简介]孙敏(1980-)，男，山东泰安人，枣庄学院数学与统计学院副教授，硕士，主要从事计算数学、最优化理论与算法的研究.

[中图分类号]O221.2 [文献标识码]A

0引言

本文，我们考虑如下无约束最优化问题

minf(x), x∈Rn

(1)

其中f(x):Rn→R1是连续可微函数. 问题(1)有很多求解有效的方法, 如共轭梯度法、牛顿法、拟牛顿法、最小二乘法等, 其中共轭梯度法由于具有存储量小, 同时又可以避免拉锯现象的优点, 被人们广泛的研究和使用. 共轭梯度法采用下面的迭代格式

xk+1=xk+αkdk

(2)

其中xk是当前迭代点,αk是步长,dk是f(x)在点xk的下降方向, 其迭代格式为

(3)

其中gk=▽f(xk),βk被称为共轭梯度参数.有很多著名的βk公式[1],如

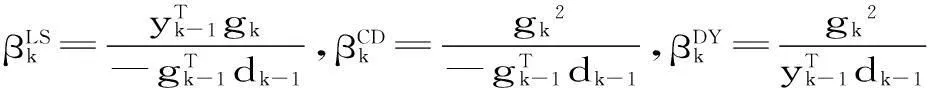
其中yk-1=gk-gk-1. 大量的研究表明,FR,CD和DY方法有较好的全局收敛性，但是数值效果不如另外三种；而PRP,HS和LS方法虽然具有较好的数值效果，但全局收敛性较差. 因此很多学者对PRP,HS和LS方法进行了研究，提出了许多修正的PRP,HS和LS方法. 本文我们考虑Wei等[2]在2006年提出的修正的PRP共轭梯度法和Wan等[3]在2011年提出的PRP型谱共轭梯度法. 先看Wei等提出的方法,其共轭梯度参数的公式为:

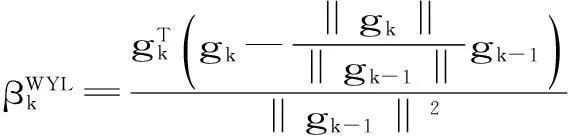
(4)

后来,Dai等[4]对Wei-Yao-Liu共轭梯度法进行了深入研究, 提出了新的共轭梯度参数公式:

(5)

其中μ>1是一个常数. 显然当采用精确线性搜索时, (5)退化成(4).Wan等[3]提出了如下PRP型谱共轭梯度法:

(6)

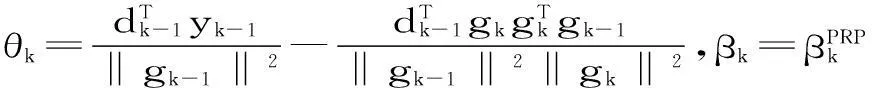
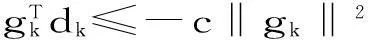
其中c>0是一个常数. 最近, 陈等[5]对将Wan等得思想应用到一类修正的Wei-Yao-Liu共轭梯度法[6],得到了一种新的PRP型谱共轭梯度法, 该算法不依赖线性搜索就满足充分下降性, 同时在标准的Armijo线性搜索下具有全局收敛性, 初步的数值试验表明了方法的有效性.

受陈等[5]所提共轭梯度法的启发, 本文对Dai等[4]提出的方法进行修正, 使其也具有不依赖于线性搜索的充分下降性, 并且在Armijo类线性搜索的条件下具有全局收敛性. 本文的结构如下, 第2节提出了新的具有充分下降性的修正类Wei-Yao-Liu共轭梯度法,并且证明了其具有充分下降行;第3节证明了新方法在一类Armijo线性搜索下具有全局收敛性; 第4节给出了初步的数值试验结果.

2修正类Wei-Yao-Liu共轭梯度法

修正类Wei-Yao-Liu共轭梯度法

步0: 取初始值x0∈Rn, 参数μ>0,ρ∈(0,1),γ>0,令k:=0;

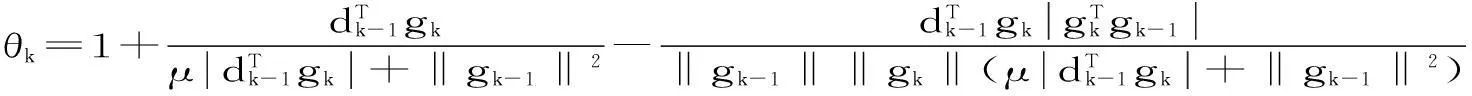
(7)

步3: 令αk是{1,ρ,ρ2,…}中满足下式的最大者α

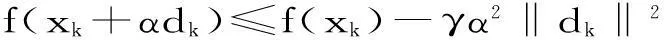
(8)

令xk+1=xk+αkdk,k=k+1, 转步1.

注1显然, 当采用精确线性搜索时, 上面的修正类Wei-Yao-Liu共轭梯度法退化成文献[7]中的改进的Wei-Yao-Liu共轭梯度法.

注2与文献[4]中的方法相比, 修正类Wei-Yao-Liu共轭梯度法中的μ的取值范围扩大了.

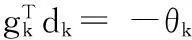
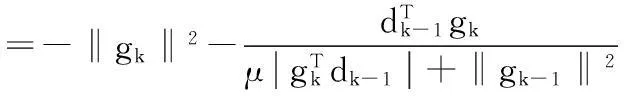
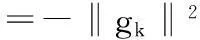
由归纳假设知命题成立.

证略.

3算法的收敛性

收敛性的证明需要下面的假设:

(H1) 水平集L0={x|f(x)≤f(x0)}是有界的.

(H2) g(x)在包含L0的开凸集N上Lipschitz连续, 即存在常数L>0, 使得

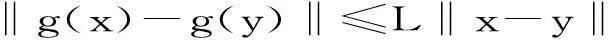
(9)

首先由(8)和(H1)可得：

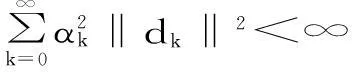
于是

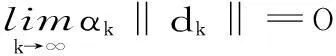
(10)

同时由(H1)(H2)可得，存在γ1>0，是得

(11)

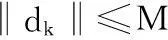
(12)

证由(5)-(7),(11), 可得

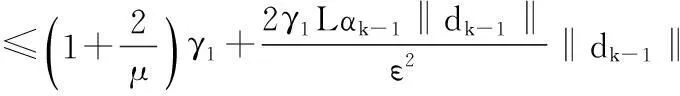
由(10), 可得, 存在常数r∈(0,1)与整数k0, 使得对于任意的k≥k0, 都有

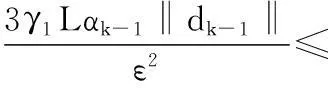
于是, 对于任意的k>k0, 有

下面我们证明新算法的全局收敛性.

定理1在(H1)(H2)下, 假设算法产生无穷点列{xk}, 则

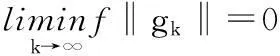
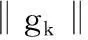
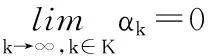
(13)

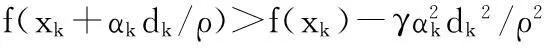
(14)

于是由中值定理, 存在hk∈(0,1), 有

f(xk+αkdk/ρ)-f(xk)=ρ-1αkg(xk+αkhkdk/ρ)Tdk

(15)

‖gk‖2≤ρ-1(L+γ)αk‖dk‖2.

4数值试验

本节, 我们从文献[6]中选取一些测试函数来检验新方法(记为算法1)的数值效果, 测试问题的初始值也由文献[6]给出. 考虑到PRP方法是目前数值表现最好的共轭梯度法之一, 同时Wan等[3]提出的PRP型谱共轭梯度法(记为SPRP)是对PRP方法的改进, 因此在下文中我们将新方法与SPRP方法作比较. 两种算法的参数设置如下:

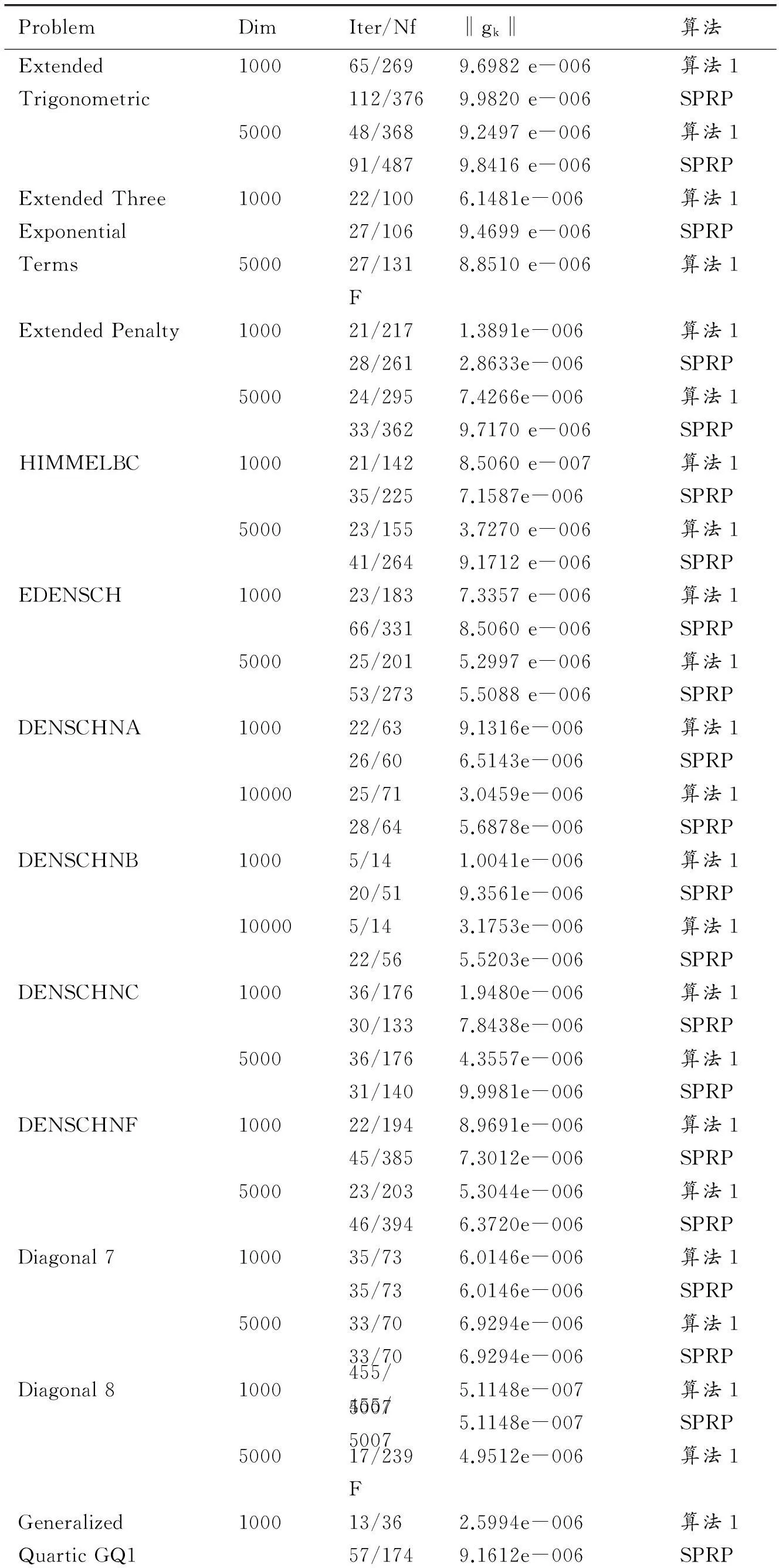
表1　算法1和SPRP的数值结果

500018/493.1550e-006算法143/1306.8811e-006SPRP

从表1的试验结果可以看出, 对于所选的测试问题, 在相同的精度要求下, 两种方法都有较好的数值表现. 特别的, 就迭代次数与函数计算次数两项评价指标分析, 算法1对文中所选的大部分测试问题, 都具有优于SPRP方法的数值效果. 另外, 实验表明, 算法1中的参数μ对实验的结果有较大影响, 因此, 为了得到更好的试验效果, 我们需要对算法1中的参数μ的选取值作进一步的研究与探索(如自适应).

参考文献

[1]Shi Zhen-Jun, Shen Jie. Convergence of Liu-Story conjugate gradient method[J]. European Journal of Operational Research, 2007,182: 552-560.

[2]Shi Zhen-Jun. A new memory gradient method under exact line search[J]. Asia-Pacific J.Oper. Res., 2003, 20(2): 275-284.

[3]Shi Zhen-Jun. A new Super-memory gradient methodfor unconstrained optimization[J]. Advance in Mathcmatics, 2006, 35(3): 265-274.

[4]Zhang Li, Zhou Wei-Jun, Li Dong-Hui. A descent modified Polak-Ribiere-Polyak conjugate gradient method and its global convergence[J].IMA Journal of Numerical Analysis,2006,26: 629-640.

[5]Cheng Wan-You. A modified and descent nonlinear conjugate method[EB/OL].[2007-12-03]. http://www.paper.edu.cn/paper.php?serial_number=200612-316.

[责任编辑：房永磊]

The Improved Wei-Yao-Liu Conjugate Gradient Method With Sufficient Descent Property

SUN Min

(School of Mathematics and Statistics, Zaozhuang University, Zaozhuang 277160, China)

Abstract:In this paper, based on design ideas of some new conjugate gradient methods, an improved Wei-Yao-Liu conjugate gradient method is proposed. The most attractive properties of the method is that the generated iterative direction is always a sufficiently descent direction without utilizing the line search. Under an Armijo-type line search, the new method has global convergence. The preliminary numerical results show that the method is effective.

Key words: Wei-Yao-Liu conjugate gradient method; sufficiently descent; global convergence