如何对数学习题进行一题多变
2016-01-09周秀静
周秀静
摘要:中考主要是考查学生的四基和四能,体现数学是解决生活中问题的工具学科。所以,在教学中教师要充分挖掘教材中典型内容的潜在智能,恰当地对它进行改变、引伸、拓广、挖掘,实现一题多变,充分发挥课本上典型习题的作用。
关键词:一题多变 中考
在数学教学中,实现一题多变,有利于培养学生的发散思维,开阔视野,全方位思考问题,分析问题;有利于培养学生的创新思维能力和解题技巧;有利于学生提高解决综合问题的能力;有利于培养学生的探索精神;有利于创新意识的形成和发展,是培养学生良好思维品质与创新精神的好方法。教学中采用一题多变的形式,可以训练学生积极思维,触类旁通。从而提高学生思维敏捷性、灵活性和深刻性。
如何进行一题多变呢?一题多变重点在于对某个问题进行多层次、多角度、多方位的探索。我以课本上的一道习题为例,浅谈一下我的做法:
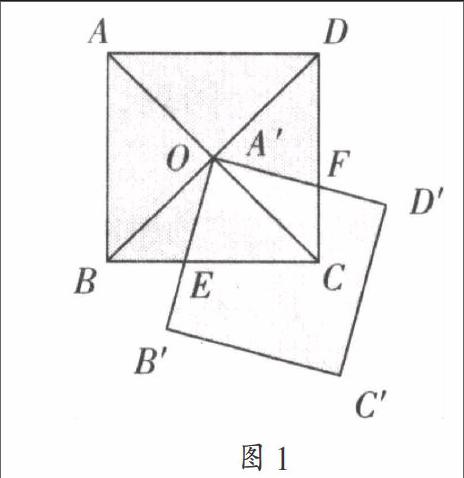
原题呈现:已知,如图1,正方形ABCD的对角线AC、BD相交于点O,正方形A'B'C'D'的顶点与点O重合,A'B'交BC于点E,A'D'交CD于点F.求证:OE=OF
分析:证明线段相等常用的方法是证三角形全等,本题可以证△OBE≌△OCF或证△OCE≌△OFD,得到OE=OF
本题来源于教材,图形简单,考查内容基础。但是由于图形是特殊的四边形---正方形,正方形具备所有特殊四边形的性质,所以对此题挖掘和延伸、拓宽,可以构架知识上和方法上一系列的知识体系,总结出这类题型的基本解题方法,方法有四种:
方法一:已知不变,直接挖掘其他结论
变式1:BE与CF相等吗?请说明理由。
变式2:求证:∠OEC=∠OFD(请用不同的方法进行证明)。
变式3:连接EF,判断△OEF的形状,并说明理由。
评析:上述三种变式都是已知条件不变,直接寻找题目中的其他结论,解题思路都可以通过证△OBE≌△OCF或证△OCE≌△OFD得到,把一题多变转化成多题一解,将有利于学生理清分析问题的思路、认识和掌握典型的解题过程,辨别不同问题的过程特点,从而掌握解决问题的一般性方法,有效他防止学生的思维定势。
方法二:改变题型。
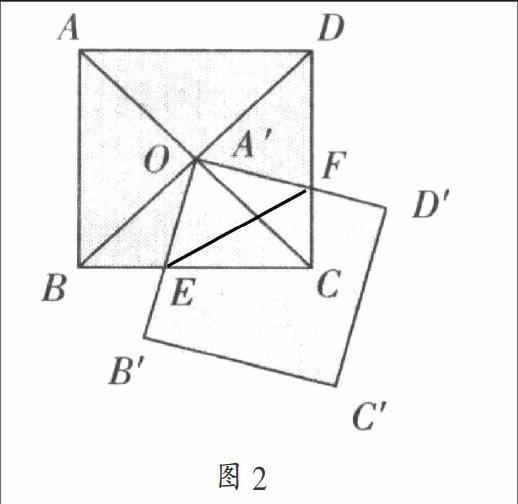
变式4:已知,如图2,正方形ABCD对角线相交于点O,正方形A'B'C'D'的顶点与点O重合,A'B'交BC于点E,A'D'交CD于点F,连接EF,若正方形ABCD的边长为12,
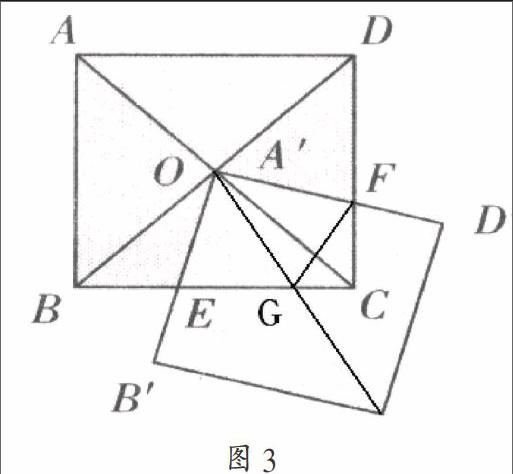
变式5:已知,如图3,正方形ABCD对角线相交于点O,正方形A'B'C'D'的顶点与点O重合,A'B'交BC于点E,A'D'交CD于点F,OC'交BC于点G,连接FG。若正方形ABCD的边长为12,FG=5,则FC= 。
评析:变式4和5都是在原题型的基础上,对原题型结论的进一步延伸探究,是原题结论的进一步拓宽,都是在原题型证明三角形全等的基础上,进一步利用原图形的特点直角通过勾股定理构造一元二次方程,建立二次函数模型。体现方程建模和数形结合的数学思想。
变式6:正方形ABCD对角线相交于点O,正方形A'B'C'D'的顶点与点O重合,正方形绕点O转动,A'B'交BC于点E,A'D'交CD于点F.
(1)若点E为BC的中点,如图4,则点F也为CD的中点吗?证明你的结论。
(3)由(1)(2)你得到什么结论?
评析:本题是对原题型的基本延伸,通过类比原题型的基本的三角形全等,得出相应线段之间的关系,体现研究数学常用的数学方法——特殊到一般的数学思想。
现在的中考主要是考查学生的四基和四能,体现数学是解决生活中问题的工具学科,原题型都来源于教材。所以,在教学中教师要充分挖掘教材中典型内容的潜在智能,恰当地对它进行改变、引伸、拓广、挖掘,实现一题多变,充分发挥课本上典型习题的作用,使学生对所变习题既有熟悉感又有新鲜感。这样不但能诱发学生的解题欲望,激发求知欲,还能起到以一当十,以少胜多的效果,增大课堂的容量,培养学生各方面的技能,特别是自主探索,创新思维的能力,把学生从题海中解救出来,充分调动了学生学习的积极性,从而有效提高课堂教学效率。
(责编 张景贤)