分散经济中的标准化

艾曼纽?奥西奥拉++米歇尔?贝南

摘要：受进化博弈论的启发，本文呈现了一个关于标准和规范如何产生于分散经济的动态模型。研究结果表明标准化结果取决于采纳者对不相容引起的问题的态度。如果个体对不相容表示厌恶，最终会导致标准化的发生，但是有时社会最后会选择次优的标准。在这种情况下，官方行动有利于迅速达成合理的标准化。另一方面，当个体对不相容表示中立或容忍时，就不存在路径依赖或锁定的问题，并且规制似乎无法更好地替代自由放任。

关键词：标准化；分散经济；质量治理

21世纪伊始，随着国际贸易增长的速度是经济增长的四倍，市场经济的全球化开始加速。在这个新的经济环境中，越来越需要标准化和合格评定来跨越之前分离的管辖范围。国际公认的标准是必要的，第一，可以方便产品对比，减少贸易的技术壁垒许多研究已经证明，同一产品在分散的市场中价格差异巨大。全国市场中存在持续的分割，原因之一就是存在着不同的产品标准（世界银行，1998）。；第二，可以促进更好的质量管理和消费者保护。超过500家组织与国际标准化组织（ISO）一同致力于标准的设立 ISO标准化过程是分散的，包含2850个技术委员会和3万名位专家。它依靠市场力量、立足于集体意见。ISO不是一个首字母缩略词，而是一个由希腊语前缀iso-构成的词语，该前缀意为“平等的”。这样，ISO组织在所有的语言就可以叫法一致，十分方便。（www.iso.ch[1999]）。。国内组织经常复制这一国际活动。例如，在美国，超过700家组织努力推进他们自己的、有时是矛盾的标准采纳规范。这些组织的激增正说明了标准化问题的重要性，也解释了设法成功解决它的不易。在当今这个技术不断发展、偏好信息广泛传播的世界，设立标准是一个棘手的事情。美国和ISO的集体意见都依赖于实际的市场力量。出于对统一的政治承诺，欧盟的许多成员国更青睐通过一个更集中化的途径来设立标准。

本文分析了分散经济中的标准化过程，强调了哪些情况下集中干预更合适而哪些情况下自由放任更可取。考虑到标准采纳的动态性，本文的分析基于进化博弈论的精神。本文的主要贡献是，展示了标准采纳者对不相容的态度是如何影响一个分散的标准化过程的结果的。

如果协同失败对用户来说成本高昂，会发生厌恶不相容。交通规则和信号、电气规范和药剂配方就是这样的情况。当人们的安全面临危险时，他们对不相容表示零容忍。如果采纳者担心标准化失败，他们会试图避免它。当存在厌恶不相容时，我们证明分散的采纳过程不可避免地导致单一标准的建立。尽管如此，预测哪一个标准最终会被选择并不总是可能的。如果可供替代的选择没有特别不同，采纳者有时会协调选择一个次优的标准。既然自由放任会导致无效率的结果，一项官方干预就有利于快速达成合理的标准化。世界上每个国家都有交通规则、电气规范和意在保护使用者的健康安全的其他强制标准。欧洲标准化委员会、美国消费品安全委员会和美国食品和药品管理局都是这些职能机构的代表，其作用就是推动产品性能标准的建立。

当存在直接的协调外部性时，会产生中立不相容。这包括一对一的交流设备、传真和计算机网络。这些商品提供用户间的直接联系。因为创建联系需要双方使用相容的技术，实现标准化非常重要。更多的用户使用一个特定的标准增加了所有使用这个标准的人能够沟通的机会。在中立不相容下，我们证明一个分散的标准采纳过程总能让一个最好的标准被选择。因此，世界上的电话、传真和计算机网络之间使用共同标准就不奇怪了。这个标准化结果会使社会福利最大化。

如果有间接的协调外部性时，会发生容忍不相容。例子包括个人电脑、音乐播放器和卡式录像机等产品。此时，消费者关心相容性因为互补品的可得依赖于初级产品的销售。随着可获得的录像带、光盘、磁带或软件的数量的增加，消费者开始对其他用户的数量不感兴趣。于是个体会挑选恰好最适合他的技术。那么，一个分散的采纳过程偶尔会引起多标准均衡就不奇怪了。当存在容忍不相容时，我们证明采纳一个单一标准不再是系统化的，甚至没必要是最优的。用户们会花时间好好体验的。只有占优势的技术会从标准化过程中脱颖而出，成为用户唯一的选择。

基于实证的视角，理论分析的结果与新技术的扩散曲线的证据相一致。众所周知，该曲线呈S型。从我们的理论分析中得出的扩散曲线也是S型。个体对不相容的态度无论是厌恶、中立或容忍都没有影响。此外，本文就设立标准时的分散化和规制的比较利益提出了特别的看法。当公共安全受到威胁时，需要有规制或强制的标准化。当存在厌恶不相容时，官方干预对加快协调并防止公共选择朝向较差的标准是必要的。另一方面，当存在容忍或中立不相容时，没有“锁定”或安全危害的风险。这与监管者或“专家”可能会不合适地代表消费者的品味和需求形成对照。规制，至少在采纳过程的早期阶段，与用户体验相比似乎是一个不那么好的选择。

与文献的关系。——经典的经济学文献依靠非合作博弈论来处理标准化问题最早见于Joseph Farrel-Garth Saloner （1985）和Michael L.Katz-Carl Shapiro（1985）的文章，“网络外部性”文章从纳什均衡概念出发论述标准化问题。关于对这一文献的评价，见《经济展望杂志》（1994年第8卷）中的网络外部性论坛。。这一支文献提供了一个详尽的关于存在网络外部性时生产者行为的研究，为标准采纳的需求方留下了一个黑箱。假设消费者同时采纳可获得的标准中的一个，正的协调外部性会产生多重均衡。在大多数情况下，学者们以分析的方法描述均衡，但是无法解决W.Brian Arthur（1988）所称的选择问题。Arthur（1988， 1989）提出以随机模型解决这个问题。他的想法是，协调外部性倾向于扩大“历史事件”——路径依赖性——并使动态在一个可能主导的标准中陷入困境——锁定性。Arthur这开创性的贡献突出了这样的事实，即标准化通常是一系列分散化选择的结果，历史会起作用。但是，他也暗示，通过他展示的案例，规制的替代选择是一个高度无法预测的、路径依赖性的分散化过程。这与直观认知中的以市场为导向的标准化并不总是不可预测的或是无效率的正好相矛盾。一个遗留问题是独立的、异质的个体实际上如何协调他们的选择，也就是说，一个特定的均衡是如何占上风的。

这个问题正是越来越多的进化博弈论和社会学习相关文献的核心，它们旨在研究具有多重均衡的博弈中的均衡选择。这些文献解释了一个均衡如何能成为学习或适应的结果，而非产生于理性反思这一支前景光明的文献中的奠基性的文章有，Dean Foster and Peyton Young （1990）， Glenn Ellison （1993）， Drew Fudenberg and David M.Kreps （1993） 和 Michihiro Kandori et al.（1993） 和其他。一个最新的文献综述（也是良好的进展），见Fudenberg and David K.Levine （1998）的著作：《博弈学习理论》。。Kandori et al.（1993）在一篇至今仍为经典的文章中已经证明，对称的博弈（包括大量目光短浅的参与者和嘈杂的突变）自然地引导在两个纳什均衡中犹豫的参与者去选择风险主导的那一个。这一贡献已经是均衡选择领域中的主要进步。他们的结果独立于任何初始条件或“历史事件”。更重要的是，在我们看来，它打开了一扇通往动态设定下协调问题的可预测理论的门。

本着这支原创且成果颇丰的文献的精神，本文重点关注异质性的个体在两个标准之间做选择时面临的协调问题。有两个时间尺度：短的一个适用于个体，更长的一个适用于社会整体。个体循序随机地采纳一个或另一个标准，这样的事实充分体现着动态维度。从他们的前任那里继承了标准化状态的“新生”采纳者不具备前瞻性，这一事实体现了两个时间维度——个人的和社会的。他们有限的寿命要求他们在短期内实现最优。你可能会困惑，是否连续的目光短浅的标准采纳会导致某种无意识的集体最大化行为，抑或相反，会引起单纯的路径依赖。答案取决于利害攸关的特定标准。

我们发现，在长期中标准采纳的随机分散过程表现一个确定性的动态过程。因为在其静态过程中，协调问题承认多重，故引入动态模型解决选择问题。只有在长期中才会产生相关的确定性过程的稳定均衡。本文的一个重要方面是，突出了个人效用函数的凹性和凸性在均衡选择中的作用。与Kandori et al.（1993）的其他所有我们知道的设定相反的是，关于选取统一标准的小部分人口的代理人效用函数不一定是线性的。我们证明了，与厌恶不相容对应的是凸曲线，与容忍不相容对应的是凹曲线，中立不相容对应线性曲线。当个体对不相容持厌恶态度时，最终会发生标准化。不过，最终被选择的标准并不总是可被预测的。均衡不一定唯一的事实暗示了这个分散化过程有时选择的是一个较差的标准。这就是Arthur（1988）描述的路径依赖和锁定的性质。另一方面，当个体对不相容表示容忍时，标准化不再是系统化的。这个采纳过程却总是可预测的。最后，当个体对不相容持中立态度，这个分散过程导致主导标准的标准化。从社会的立场来看，这是一个最优结果。

本文结构安排如下：第一节描述模型，第二节展示关于随机过程收敛的一般结果，第三节导出均衡和扩散曲线，第四节描述最优解并与第三节的均衡对照，第五节是结论。

一、模型

我们选取了一个包含A、B的两个可供选择的不相容标准的离散选择模型。采纳者对一单位的“好标准（利益）”的需求无弹性。他们的偏好用参数表示为δ∈[0，1]，我们称此为一个“类型”。术语δ可被理解为决定代理人的适应成本，这是由他们不得不接受一个（对他们来说）不完善的标准而非享受他们理想的标准所引起的，后者本已经落在δ上。也就是δ是个体与标准A的“距离”，落在0点上；1-δ是个体和标准B的距离，落在1上。此外，采纳者对A或B的偏好取决于各标准享有的市场占有率，分别用xA和xB表示。一类δ代理人对标准k （=A， B）的偏好由效用函数 k→ （1-δk） uk （xk），δA = δ，δB = 1 – δ。函数uA和uB被定义为购买此标准的净价格价格可以是固定的或随着时间变化而变化，只要净效用函数满足假设1。这不仅包括非专属标准（例如打印机键盘布局、螺纹规格、铁路轨距和计算机文件相容格式如ASCII），也包括很多专属标准。确实，大多数标准化博弈不允许存在多个赢家，因此价格竞争十分激烈（即具有Bertrand类型的性质）。例如，在VHS/Beta关于录像带格式的大战中，S.J.Liebowitz and Stephen E.Margolis （1995） 证明两种技术总以差不多相同的价格零售，以至于不能认为价格在消费者做决定时发挥了可区分的作用。。于是出现了这样的结果，类型δ代理人更偏爱标准和市场占有率的组合，当且只当它对该代理人产生一个更高的效用：

（A， xA） ≥ δ （B， xB） <=>

（1 - δ） uA（xA） ≥ δuB （xB） （1）

函数uA和uB对所有代理人相同但互相之间不一定相等，满足下面这一假设。

假设1：uk（0）=0 且 uk （x）>0 ?x ≥ 0 （k= A， B）。

根据假设1，使用一个给定标准的人群占比越多，每个采纳此标准的个体获得的净收益就越大。换句话说，也就是存在正的网络外部性。该假设与博弈论中关于学习和进化的相关文献相符。在所有文章中，包括Kandori et al.（1993），一个代理人从采纳一项技术中获得的收益随其他同样采纳它的人群的比例增加而增加。但是，在这些文献中，包括在那些网络外部性的文献中，支付都是市场占有率的仿射函数。在博弈论中关于学习的文献中，支付矩阵独立于参与者的策略（即它们影响支付概率而非支付本身），这个假设是自然而然的。在一个标准采纳的协调博弈中它就不那么有说服力了，因为在这种情况下个体收益直接取决于做出相容选择人群的比例。我们考虑了任何满足假设1的函数uk，包括凹函数和凸函数 本文还考虑了异质性的代理人（也就是说，不是所用人都有同样的δ），而Kandori et al.（1993） 考虑的是同质性的代理人。因此，在Kandori et al.（1993）的文章中，采纳策略的支付k = A， B对所有βk>0的代理人αk + βk 适用。此外，本文考虑了所有代理人之间的网络外部性，而Kandori et al.（1993） 中的相互作用是严格双边的。。

设 为时间t时的边际消费者，即对任何一个标准都没有特别偏好的人。通过公式 （1），为（1 - δ） uA （ ） = δ uB （ ），也就是：

（2）

我们推导出，一个代理人δ在日期为t+1 时进入市场，如果δ ≤ 则选择标准A，反之选择标准B。这类行为就被称为目光短浅，因为该代理人没有试图将他的决定融入进该标准将来会演化的方式。实际上，当消费者面临一个新的采纳选择，他们极大地折现了未来，这绝大部分是因为他们预期到了淘汰的现象。在这篇文章中，我们以极端的视角认为采纳者的心理折现因素是无穷大的。这暗示着，在过去的条件下，他们的采纳选择是确定性的 循着George Ainslie （1975） 的研究，心理学者们已经强调了“随着收益自选择时就被延迟，收益的有效性下降”，因此挑战了一个指数分布函数的假设。参数研究和实验甚至已经发现了适用于人类和某些动物的双曲贴现函数。实际上，消费者并不是不变的，他们也知道这一点，所以他们只能在短期内实现最优。相关文献回顾参见Ainslie （1992） 和 George Loewenstein and Drazen Prelec （1992）。关于目光短浅行为的假设的有趣讨论可见 Kandori et al.（1993） 和 Fudenberg and Levine （1998 第4章）。。相反的是，决定他们的进入（采纳者的顺序）的规律是外因的且随机的。“自然”决定了谁会下一个进入。根据一个累积分布函数被设为F（·）的有界密度函数 f（·），采纳的候补标准分布在区间[0， 1] 上。

假设2：根据一个有界密度f （·），δ分布在[0， 1] 上。

因此，一个在第t+1轮进入市场的个体会选择标准k的概率就是，对于标准A，PA （ ） = Prob （δ ≤ ），对于标准B，PB （ ） = Prob （δ > ） = 1 - PA （ ）。我们从假设2和公式 （2） 中推出：

PA （ ） = F（ ） （3）

在假设1下，概率 （ ） 在标准k的市场占有率中增加（故而在另一个标准的市场占有率中减少）是很容易检验的。这是自然的，因为个体的决定由于正的协调外部性而形成。让我们现在检验一下，连续的采纳选择最终是如何聚集形成一个集体选择的。

二、宏观结构的产生：一个（路径依赖的）强法律定理

动态模型如下所示。时间是分散的，其范围是无限的。周期t = 1， 2， ……指第t轮的标准采纳。采纳者进入市场的比率是不重要的（除了注意收敛时间时）；有关时间并不是指时钟的时间，而是事件的时间。在每一轮采纳时，一个由δ鉴定的代理人根据概率密度 f随机地从采纳者总体中抽出。采纳者的顺序由外因决定的且是随机的。代理人根据各标准的现有市场占有率和他们自己的特定偏好，从各标准中做出决定。对于在一个给定日期t+1时的一个给定个体δ ，如果δ ≤ 她会采纳标准A ，反之采纳标准B。

使 ≥ 1为标准k（= A， B ） 的采纳者的初始数。从技术层面上看，它可以是任何一个比1大的整数。不过为了便于分析，集中在两种情况似乎更自然： ， 都很小，如引入一项新技术的两个变体； 很小 很大（或反之），如当一项新标准开始挑战已经根深蒂固的标准。此外，设已经在时间 t 时采纳标准k代理人的累计数为 ，到时间 t为止已经发生的标准采纳的累计数为 。我们认为 = +t。

标准k在时间t时的市场占有率是 = 。从公式 （3）可知 ，设 为标准k 会在第t+1轮采纳时被选择的概率，故市场占有率的动态由下面的公式给定：

= ，概率为 （4）

，概率为

设 = 。那么方程组（4）可改写为以下形式：

（1 - ） + 概率为

=

（1 - ） 概率为 （5）

我们从方程组 （5） 中可以推演出关于现有状态时的市场占有率的预期波动。我们得到：

E （ | ） = + （ - ） （6）

公式 （6） 的解释是直观的。如果标准k被采纳的概率大于它现有的市场占有率，标准k的市场占有率的增长是意料之中的。否则，它的市场占有率会减少；当 > 时， （ - ）项为正，当 时为负。确实，如果一个标准的市场占有率比它被采纳的概率小太多，那么该标准基于平均被选择的概率高于按其现有的市场占有率被选择的概率，因此它的市场占有率会增长。同理可证，如果一个标准的市场占有率比它被采纳的概率要大太多，那么该标准的市场占有率会下降。直觉告诉我们该方程组会在采纳概率和市场占有率相等时达到均衡。这个推测被证明是正确的。

设单位单形为Δ1 = { （x， y）； x ≥ 0； y ≥ 0 且x + y =1 }。概率函数P = （ PA， PB）从公式 （3） 中推导而得，将市场占有率的单位单形映射入概率的单位单形。我们将随机过程 （5） 关联定义在Δ1（市场占有率的单位单形）上的定率系统，它由下面加点时间导数的常微分方程 （ODE） 给出：

xk= Pk （xA， xB） - xk k = A， B （7）

方程组 （5） 的市场占有率矢量xt= （xtA，xtB） 趋近于常微分方程 （7） 的均衡时，定理1成立。

定理1 （Bruce M.Hill et al.， 1980）：

（i）假设P：Δ1 →Δ1，将市场占有率的单位单形映射入概率的单位单形的概率函数是连续的。那么市场占有率矢量xt= （ ， ）与概率1趋近于常微分方程 （7） 的一个均衡 （ ， ）。

（ii）假设P 将单位单形的内部映射入它自己，且 （ ， ）是常微分方程 （7） 的一个稳定均衡（如以常规方式定义的那样）。另假设初始市场占有率（ ， ）属于该单形内部。那么过程（ ， ）趋近（ ， ）的概率为正。

（iii）假设（ ， ）是常微分方程（7）的一个不稳定均衡。那么该过程趋近（ ， ）的概率不为正。

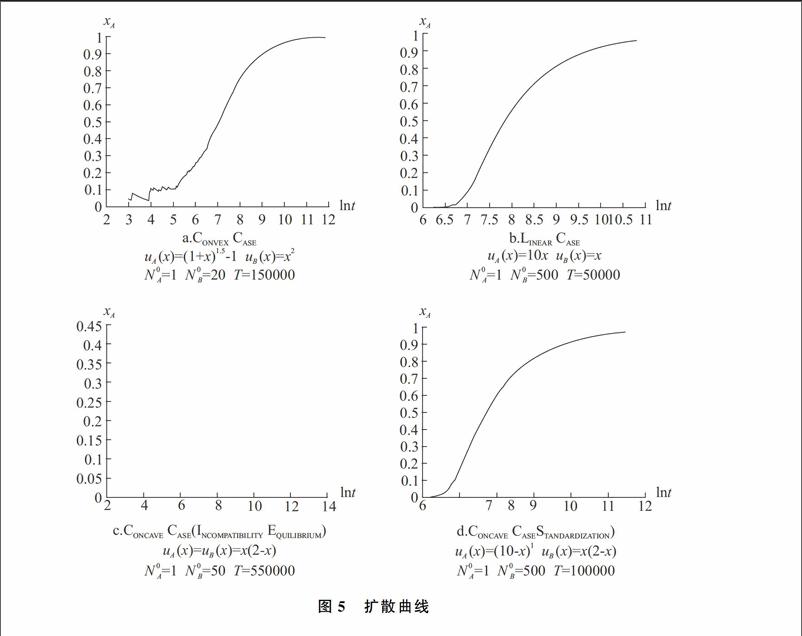
由于定理1，研究关联的确定性系统 （7） 的收敛性是充分的，不用研究随机过程 （5） 的收敛性。为了理解这一点，我们假设在这个竞争过程的开始，用户的初始累计数N0 很小（例如两个标准为成为市场标准而竞争）。于是市场占有率的变动时常大涨大跌，波动剧烈。当用户的累计数很小时，每次新的采纳都使市场占有率猛增。然而，每次新的采纳对市场占用率变动的影响随着采纳数减少：第一个采纳者拥有极显著的影响，而第一百万个的影响几乎可以忽略不计。久而久之这会产生随机性的动态抑制这与Kandori et al.（1993）中提到的变异概率的抑制相反。他们考虑的是一个静止的和遍历的模型，其中人群规模固定且每个代理人偶尔会突变。那么，采纳每项技术的代理人比例的随机性通过突变加入到方程组中。因此不收敛。但是，通过使突变率像一个比较静态运动一样趋近于0，并描述遍历分布的极限的特征，一项特定技术的选择是确定的。。受质量惯性的限制，该随机过程最终由等价的确定性系统 （7） 指挥。 图5a 阐明了这些波动和其抑制 图5a展示了标准A的随机市场占有率的发展，标准A适用于一个初始数量的采纳者=1，= 20，效用函数uA（x） =1 （1 + x）1.5 – 1，uB（y） = y2。标准采纳的最终数是150021。时间规模是ln（ t + 21），t为采纳数。。值得注意的是，在二次效用函数的情况下，uA（x） = ax2 且 uB（y） = by2，且它们均匀分布，对于在进行一个对称的2 × 2协调博弈[即，伴随收益：∏ （A， A） = a， ∏ （B， B） = b， ∏ （A， B） = ∏ （B， A） =0]的一个同质总体，等式 （7） 给出了模仿者动态。那么，公式 （7） 变成： = x（ax – （ax2 + b（1-x）2 ） ）。因此本文向连续时间的模仿者动态的研究提供了一个新的微观基础，它可以作为包含分散时间中的异质采纳者的一个随机模型的极限生成 感谢匿名评审指出了这一事实。欲知更多关于模仿者动态的详情，参见Jorgen W.Weibull （1995） 和 Fudenberg and Levine （1998）。。

在经典博弈论中，不动点是均衡的候选。但是，不是所有的不动点都可被选为均衡：只有稳定的不动点才符合条件。如果在点上 - 1 ≤ 0，常微分方程的一个均衡 局部稳定（否则它局部不稳定）。根据公式 （6），如果一个标准在一个均衡附近被采纳的概率大于其市场占有率，该标准会越来越多地被采纳并会偏离均衡。这暗示着 会从一个局部不稳定的均衡偏离，并收敛至一个局部稳定的均衡感谢匿名评审建议讨论均衡的稳定性。。如果这个确定性系统只有一个稳定的不动点，均衡是可预测的。无论初始条件 和 是什么，该系统都会收敛至这个不动点。另一方面，如果这个确定性系统有多个稳定的不动点，由于一开始的波动，结果是无法预测的。这种情况下，取决于初始条件，结果可以更加精确。令x* = （ ， ）为（7） 的一个稳定均衡。我们以B（x* ） 定义x*的吸引区域，点x的集合的常微分方程的前向轨迹被x* 吸引。那么，B（x* ） = { x∈ Δ1 | limt→∞ x（t） = x* }，函数x（t） 表示以x（0） = x （ x是初始市场占有率的矢量） 为初始条件的等式 （7） 的解。下面的定理由 Benaim （1999） 的研究中推导得出。

定理2：令x*∈Δ1为常微分方程 （7） 的一个稳定均衡，Q ? B（x*） 为x*的吸引区域的一个紧子集。存在一个正数k，唯一依赖于Q，因此：如果在时间T≥ 0时，采纳的总数是 = ，且市场占有率矢量（ ， ）属于Q，那么：

.

定理2给出了之前描述的“质量惯性”原理的一个定量解释。如果在第T轮的采纳时，市场占有率接近一个稳定均衡x*，没什么可以排除采纳的随机过程跳入另一个吸引区域确实，根据定理1的推断（ii），该事件发生的可能性概率为正。。但是，时间T时的用户累计数NT越大， 这一跳跃的概率越小。

三、均衡

为了识别可能作为调整的随机过程的长期结果而产生的标准，根据定理1我们只需要研究P 的不动点。均衡的候补是 PA （x， 1 - x） = x [或者等价地，PB （x， 1 - x） = 1 - x] 的解。从等式 （3） 中我们推导出：

x = F （8）

长期均衡的候选是一个静态协调博弈的纯策略均衡。在一个所有人同时采纳的博弈中，如果没有个体“会希望从那个他想得到的标准叛逃至一个不同规格的好标准，在这个（均衡）假设下他会是唯一的叛逃者”（Farrell and Saloner， 1986）。静态博弈的纯策略均衡构成了等式（8） 的静态博弈的解，检验这一点是很容易的。特别是，PA （1， 0） = 1 （关于A的标准化）和PA （0， 1） = 0（关于B的标准化）总是均衡。此外，依赖于函数uA、uB 和F，不相容解总是存在的。为了分析这些，我们在下面的部分里假设代理人在[0， 1]上均匀分布。

假设2`：δ在[0， 1]上均匀分布。

这暗示着每种类型的代理人倾向于平等地进入市场。在假设2`下，等式（8） 直接变为：（1 - x） uA （x） = x uB （1 - x）。这使我们可以集中在由uA、uB代表的个体偏好对标准化的影响上。本着不确定性相关文献的精神，我们引入容忍和厌恶不相容的定义。

定义1：在选择了标准A或B之后，考虑这个选择与一个总体匹配，这个总体或者 （i） 有μ的概率每个人都使用标准A，有（1-μ） 的概率每个人都使用标准B；或者 （ii） 其中有 μ% 的人使用标准A，（1-μ）% 使用标准B。如果一种对标准的态度引起一种对 （i）的严格偏好，它被称为是“不相容-厌恶”。如果引起对（ii）的严格偏好则被称为“不相容-容忍”。导致其他情况的被称为“不相容-中立”。

协调外部性形成偏好的方式取决于个体如何协调以及为何协调。例如，在选择了一辆左座驾驶或右座驾驶的交通工具后，该选择被发送给一个城市，这个城市中或者（i） 有1/2的概率每个人都在道路左边驾驶，有1/2的概率每个人都在道路右边驾驶，或者（ii） 一半的人靠左行驶，一半的人靠右，所有的人会选择（i）。另一方面，当有一个类似的选择，Macintosh台式电脑技术对比一个相容IBM的格式，大部分人会选择（ii）。显然，个体对不相容的态度取决于利害相关的标准的性质。

如果协调失败会令用户付出高昂代价，他们对标准化的态度会是不相容-厌恶。如果不完善的标准化使他们面临危险，这种情况就会发生，比如海陆空交通规则和信号，用火用电规范，以及药物配方或化学式。1842年的巴尔的摩大火就是一个很好的例子。正如Samuel Krislov （1997） 回忆的那样，“综合区域的消防部门赶来帮忙，但只能无助地站在一旁，因为他们的水龙带联轴器和当地设计不相容。”这就是一个典型例子，即使是对较差的水管设计进行标准化，也会比不相容要好得多。另外一个例子是1912年“泰坦尼克号”的惨痛损失。“加利福尼亚号”当时距“泰坦尼克号”只有几英里远，如果她能收到“泰坦尼克号”的SOS呼救，就能挽救成百上千条生命。1914年在伦敦签订的国际海上人命安全公约（SOLAS） 决定，大型船舶24小时都要保持无线电值班。这条规定从那时起便开始生效。

与此相反的是，当协调失败对个体的成本很小时，他们对不相容的态度是容忍的。这种情况发生在当与一项新采纳相关联的收益随着大量采纳而停滞的时候。例子包括录像机、CD播放器，或个人电脑。当互补品（即录像带、CD光盘或软件）的数量很多时，用户不能从更多的新采纳中获益。在他们看来，协调的增益是间接的，标准采纳存在规模收益递减。最后，当对一个固定的总体来说，与一项新采纳相关的边际收益是恒定的时候，个体对不相容的态度是中立的。电话、传真或计算机网络就是这样的例子，因为对于一对一的沟通，每个用户都同等重要。对于提供直接沟通服务的设备，采纳的规模收益不变，这就是中立不相容的特征。

对不相容的不同态度形成了个体的效用函数。根据定义1，容忍不相容引起（ii）的严格选择。这等价于μkuk（1） + （1-μk） uk（0） < uk（μk） ?μk∈（0，1）。对所有的μk∈（0，1），这个不等式成立的一个充分条件是uk的严格凹性。换句话说，uk的凹性表示容忍不相容。类似地，uk的凸性标志着厌恶不相容。其实，uk的严格凸性意味着μkuk（1） + （1-μk） uk（0） > uk（μk） ? μk∈（0，1），这会导致（i）的严格选择。最后，导致中性的中立不相容，等价于线性函数：μkuk（1） + （1-μk） uk（0） = uk（μk） ? μk∈（0，1）。在下文中，我们区分这样两种情况：uA （·）和uB （·）都是凸性或线性的；uA （·）和uB （·）都是严格凹性的。下文会证明，这个区别十分重要。

A.厌恶和中立不相容

首先，考虑效用函数是线性的情况，也就是uA（x） = ax，uB（x） = bx，且它们两两相等，a=b。这暗示着在公式 （3） 中，PA（x， 1 - x） = x?x∈[0，1]：任何市场占有率的分配x∈[0，1] 是常微分方程 （7） 的一个稳定均衡，并且由于定理1，它还是市场均衡的一个潜在候补。当个体表示中立不相容时，且标准是一个完美替代时，问题是退化的。下文中，我们基于它是非泛类型的从而排除了这种情况。实际上，各标准之间总有区别。但是如果a 和 b非常类似，但实际上并不完全相等，这个均衡是唯一确定的如果a > b，会发生关于A的标准化；如果 a < b，会发生关于B的标准化。。在线性的情况下，我们提出：

假设3：a≠b

当效用函数是凸性或线性时，就市场占有率而言，与新采纳相关的边际收益随着采纳者的数量增加而提高。个体从标准化中获得的收益是巨大的。他们将从与一个不相容均衡相关的多样化中获利并最终驱使分散化的调整过程向标准化变动，这是直观的。

命题1：当效用函数为凸性或凹性时，标准化随概率1发生。然而，被选中的标准不总是可预测的。它是

A或B，如果：

≤ （1）（AN1）

是A如果： （AN2）

是B如果： （AN3）

证明（见附录A）。

当个体对不相容的态度是厌恶或中立时，存在一个拐点解。此时正的协调外部性足够强大，可以推动分散的采纳过程向标准化运动。图1描述的就是被选中的标准所依赖的条件。

对这些条件的解释如下。条件（AN1）指明与标准A的采纳相关的效用是，在完全相同的市场占用率的情况下，与标准B的采纳相似。也就是说，uA（x） 和uB （x） 有相似之处。当任何一个标准都不比另一个更好时，知道采纳者的行为和掌握标准的特点都不足以预测均衡。取决于初始条件和第一轮采纳的实际情况，两项技术中的一个最终都可能变成实际上的标准。这种情况符合Arthur （1988， 1989） 的描述。收益增加或恒定恶化了“历史事件”，因此，其中一个标准偶然地获得一个采纳优势，它提高了它的领导力并最终占据了整个市场。一个极端例子是被假设3排除的路径依赖，可见于线性的情况；（AN1） 等价于 a=b当a=b时，依赖于“历史事件”，任何市场占有率的分配可能以均衡结束。。Paul A.David （1985） 用QWERTY打字机键盘布局被美国国家标准取代的例子，精妙地解释了路径依赖和锁定性质。

另一方面，条件 （AN2） 意味着，对于完全相同的市场占有率，从标准A的采纳中获得的效用总数总是比从标准B的采纳中获得的要大 [在条件 （AN3） 下反之亦然]因为效用函数递增且为凸性，（AN2） [和 （AN3） 分别] 意味着连接（0， 0）和 （1， （0）） [（0， 0）和 （1， （0））] 的直线总在曲线 uA（x） [uB（x）]下方；见图1。此外，因为uB（1） ≥ uB（x） ?x∈[0，1]，（AN2） [和 （AN3） 分别]暗示着uA（1） >uB（x） ?x∈（0，1][uB （x） >uA （x）]。。例如，在线性的情况下，（AN2） 等价于 a>b 和（AN3） 等价于b >a。于是我们说标准A相比标准B（分别地，标准B相对于标准A）有一个显著优势，因此它足够好，可以不依赖于初始条件（ ） 将竞争者排挤出市场。在电信行业，这样的一个显著优势的一个例子就是电话和电报的对比。