基于快速Delaunay三角化的散乱点曲面重建算法

2016-01-08杨军,林岩龙,李龙杰等

计算机工程与科学 2015年6期

基于快速Delaunay三角化的散乱点曲面重建算法*

杨军，林岩龙，李龙杰，王小鹏

(兰州交通大学电子与信息工程学院，甘肃兰州 730070)

摘要：针对现有三维重建算法速度较慢的问题，提出了一种基于快速Delaunay三角化的散乱数据点的三维重建算法。首先，提出一种新的平面Delaunay三角化插入点目标三角形定位算法，利用插入点的方向搜索线与三角形是否相交以及交点个数加速目标三角形定位，不用额外判断点是否在三角形内；其次，自动检测曲面漏洞，利用凸壳的边界拼接方法进行漏洞弥补。实验结果表明，本算法不仅能较好地重建出三维模型，而且有较高的效率。

关键词：曲面重建；散乱数据点；Delaunay三角剖分；漏洞填充

中图分类号：TP391.4 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.023

收稿日期：*2014-03-25;修回日期：2014-06-30

基金项目：国家自然科学基金资助项目(61462059)；中国博士后科学基金面上项目(2013M542396)；人社部留学人员科技活动项目择优资助(2013277)；甘肃省自然科学基金资助项目(1208RJZA243)；陇原青年创新人才扶持计划资助项目(201182)

作者简介:

通信地址：730070 甘肃省兰州市兰州交通大学研究生院

Address:Graduate School,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,P.R.China

AsurfacereconstructionalgorithmforunorganizedpointsbasedonfastDelaunaytriangulation

YANGJun，LINYan-long，LILong-jie，WANGXiao-peng

(SchoolofElectronic&InformationEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China)

Abstract:To solve the problem of low efficiency in three-dimensional reconstruction, we propose a surface reconstruction algorithm for unorganized points based on fast Delaunay triangulation.First,a new algorithm is designed for searching the target triangle of an inserted point in the plane Delaunay triangulation.The number of intersection points of the direction searching line of the inserted points and the triangles is used to speed up locating the target triangle.No extra work is required to determine whether the point is inside the triangle.Second,the holes on the mesh are detected automatically and they are made up by the boundary combination method of convex hull.Experimental results demonstrate the high quality and the efficient performance of the proposed algorithm in processing 3D reconstruction for unorganized points.

Keywords:surfacereconstruction;unorganizedpoints;Delaunaytriangulation;holesfilling

1引言

随着激光扫描设备的发展，三维表面采样数据的获取有多种途径，主要有医学图像、三维数字扫描仪、雷达和超声波定位仪以及数字曲面模拟等等。根据所获得数据点集的组织形式的不同，可以将点集大致分成三类，即点与点之间毫无内在联系的散乱点数据(ScattedData)、来自于医学图像的体数据(VolumetricData)和由三维激光扫描测距技术获得的深度数据(RangData)，这三种数据类型可以相互转化，比如体数据和深度数据都可以转换为散乱点数据。散乱点数据的三维重建算法研究可以提高曲面重建算法的适应性，在许多领域具有重要意义。例如，在逆向工程领域中建立产品的数字化模型；在医学领域中根据测量的数据建立人体以及骨骼和器官的计算机模型等。

目前，关于散乱点的三维重建主要有四类方法。第一类方法是构建点到物体表面的有向距离场，该距离场的零等值面即为重建曲面[1,2]，但是这种方法涉及等值面的抽取，重建比较耗时，且对边界或尖锐部分的重建结果不够理想。第二类方法是采用隐函数法进行散乱点重建。FoleyTA[3]综述了隐式曲面和参数曲面重建的有关算法;文献[4,5]通过Wendland紧致支集径向基函数方法从大量散乱点中重建了隐式曲面，该算法被KojekineN等人[6]做了进一步改进，但是支集的半径必须为全局的，对高度非一致的散乱点集算法不具有良好鲁棒性；CarrJC等人[7]利用快速多级RBF计算技术提高重建效率，但是算法步骤比较复杂；文献[8]提出一种基于径向Hermite基函数隐式拟合点云数据的方法，但基函数构造比较复杂；杜新伟等人[9]通过划分将点集分为一个由粗糙到精细的分层结构，针对给定的误差限对每个分层的数据进行插值，并将其插值结果作为前一层插值的弥补，这种方法可以在较少采样点的情况下达到较好的重建结果;其后，该算法又被进一步改进，在以前工作的基础上通过增加少量离面点，并利用曲面导数等信息，降低求解方程组阶数，进一步提高重建速度[10]；文献[11]针对传统径向基函数在重建复杂曲面时效率低下的问题，引入分块思想，针对每个子块使用不同的隐函数进行插值，并在边界处利用窗口函数进行权值约束求和得到全局插值函数，最终利用MC方法输出三角网格曲面，这样不仅降低了每个包围盒内隐函数的求解复杂度，而且此方法也适用于并行计算，对规模较大的模型有较好的重建效率。第三类方法是应用Vorionoi图对散乱点进行三角化。LawsonCL[12]提出了三角化的最大角最小化原则;SibonR[13]证明了Delaunay三角化是符合这一原则的唯一形式;GreenPJ和SibonR[14]实现了二维空间的Voronoi图的计算以及Delaunay三角化;BowyerA[15]和WatsonDF[16]将结论推广到任意维，但这种方法包含过多冗余的三角形或四面体。第四类方法是映射法，即将散乱点投影到二维空间，将二维的三角化结果反投影到三维空间来实现三维散乱点的曲面重建。田军委等人[17]在理论上证明了这种方法的正确性；文献[18]利用邻近点集反映出的局部几何信息，在切平面完成投影并进行Delaunay三角化，最终通过自动矫正局部数据点的非法连接关系，以增量扩张的方式实现局部三角网格的拼接，完成整个曲面的重建。但是，这种方法在平面Delaunay三角化时速率比较慢，而且容易产生伪漏洞(真实模型不存在的漏洞)。

本文在局部网格拼接技术的基础上，提出了一种新的三维曲面快速重建算法。在完成k邻域搜索的前提下，利用局部的邻域信息估算某点的近似法向量，并完成局部的切平面投影。提出一种新的目标三角形的快速定位算法，利用搜索方向线和三角形的交点个数完成三角形的快速定位。在平面三角化过程中加入对特殊情况的处理，使细节特征更加明显。自动检测曲面漏洞，利用凸壳边界拼接技术完成漏洞弥补。

2算法实现

2.1相关概念

给定未知曲面F的散乱点数据集S={pi|i=1,…,n}，其中pi的三维坐标值为(xi,yi,zi)，n为点集内点的数量。以下介绍重建过程中的几个基本概念。

2.1.1点的概念

在三角形T中，若某一采样点p为T的一个顶点，则三角形T称为p的邻接三角形。若三角形T中存在以p0、p为顶点的边，则顶点p0称为p的邻接点。顶点p0对于p的邻接度是指在三角形网络中含有以p0、p为端点的边的三角形个数。

根据上述邻接点和邻接度的定义，本文将点分为三类：一类是孤点，它没有邻接点；另一类是边界点，它的邻接点的邻接度为2或1；第三类是内点，它的所有邻接点相对它的邻接度都为2。在一个封闭的流形曲面三角网格中，所有顶点的邻接点的邻接度都为2，即所有点都是内点。

在平面Delaunay三角化过程中，对任一插入点p，以p为中心，以边长l形成一个四边形，此四边形称为p的自身小四边形，自身小四边形主要用在平面三角化过程中定位目标三角形的预筛选上。p和首三角形重心的连线称为p的搜索方向线。

2.1.2空间三角形的重叠

在本文中, 两个空间三角形T1、T2相互重叠是相对于某一顶点而言的。设p∈S 是曲面网格上的一个顶点，曲面在p点处的切平面为Fp，如果T1、T2在Fp上的投影相互重叠(除共享点及共享边外)，称T1、T2关于p 相互重叠。

2.2近似法矢量计算

在点集k邻域搜索完成的前提下，通过每个点p的k个最邻近点来估算p点处的近似法向量。已知p的k邻域Nbhd(p)={qi|i=1,…,k}, qi∈S，求p的近似法向量N，也就是使式(1)最小：

(1)

使用最小二乘法可得3×3阶矩阵C，即:

(2)

容易证明将C的最小特征值对应的特征向量单位化即可作为p的单位法向量的近似值。

2.3平面Delaunay三角化

逐点插入法由于其思想简单、占用内存少等优点而被广泛应用，但其本身也具有时间效率差等不足。通过对插入点算法的分析可知，算法的时间消耗主要集中在插入点对目标三角形的定位上。为此，本文提出一种新的目标三角形定位算法以加快Delaunay三角化。

2.3.1目标三角形的快速定位算法

目前，绝大多数学者对逐点插入算法的改进都集中在插入点对目标三角形的定位上，已有文献都利用点和线的相对关系在搜索方向线上进行最短路径搜索。但是，这种方法存在一些缺陷，比如插入点的搜素方向线和三角形某条边重合，或和三角形某个顶点相交等，这些情况下算法的最短搜索路径不唯一，甚至还可能出现死循环等情况。许多学者为了解决这一问题对算法进行了诸多改进，如刘少华等人[19]在相交的顶点p处按逆时针搜索此顶点的邻接三角形，然后判断点是否在三角形内，若在内则结束算法，若不在，则判断p的对边和搜索方向线是否相交，若不相交，则对下一个三角形进行判断，若相交，则把此三角形作为当前判断的三角形，纠正搜索方向线，重新按上述方法进行目标三角形定位。通过这种方法可以有效地解决搜索方向线和顶点相交时搜索路径不唯一的情况，但是如果方向线和三角形顶点频繁相交，则判断过程比较耗时，而且在每次定位过程中需要额外判断点和三角形的关系，造成了一定的时间浪费。本文首先利用插入点的小四边形和三角形重心的位置关系完成三角形的预筛选；其次，根据重心和插入点的最小距离确定搜索判断的首三角形；最后，利用搜索方向线和三角形三边是否相交以及相交点个数来判断点是否位于三角形内，并进行快速定位，不需要额外判断点和三角形的包含关系。算法的实现过程如下：

(1)利用插入点p的小四边形限定首三角形的搜索范围，选取其重心离p距离最近的三角形T作为搜索判断的首三角形。

(2)T的重心和p连接生成搜索方向线，若方向线和首三角形不相交，则p位于T中，算法结束。若和T中某条边e相交，则计算搜索方向线和边e邻接三角形T0的交点个数，若个数为1，则p 在T0中；若交点个数为2(相交边分别为e、e1)，则继续判断和边e1的邻接三角形的交点个数，直至算法结束。若搜索方向线和首三角形相交但交点为三角形的顶点p0，则按逆时针方向搜索p0的对边e，判断e和搜索方向线是否相交；若e和搜索方向线不相交，则对p0的下一个对边判断，若相交且交点不是顶点，则直接对该边的邻接三角形进行判断，若相交但交点仍是顶点，则按上述方法继续判断。

(3)完成插入点目标三角形定位。以图1为例对本文算法的定位过程进行描述。

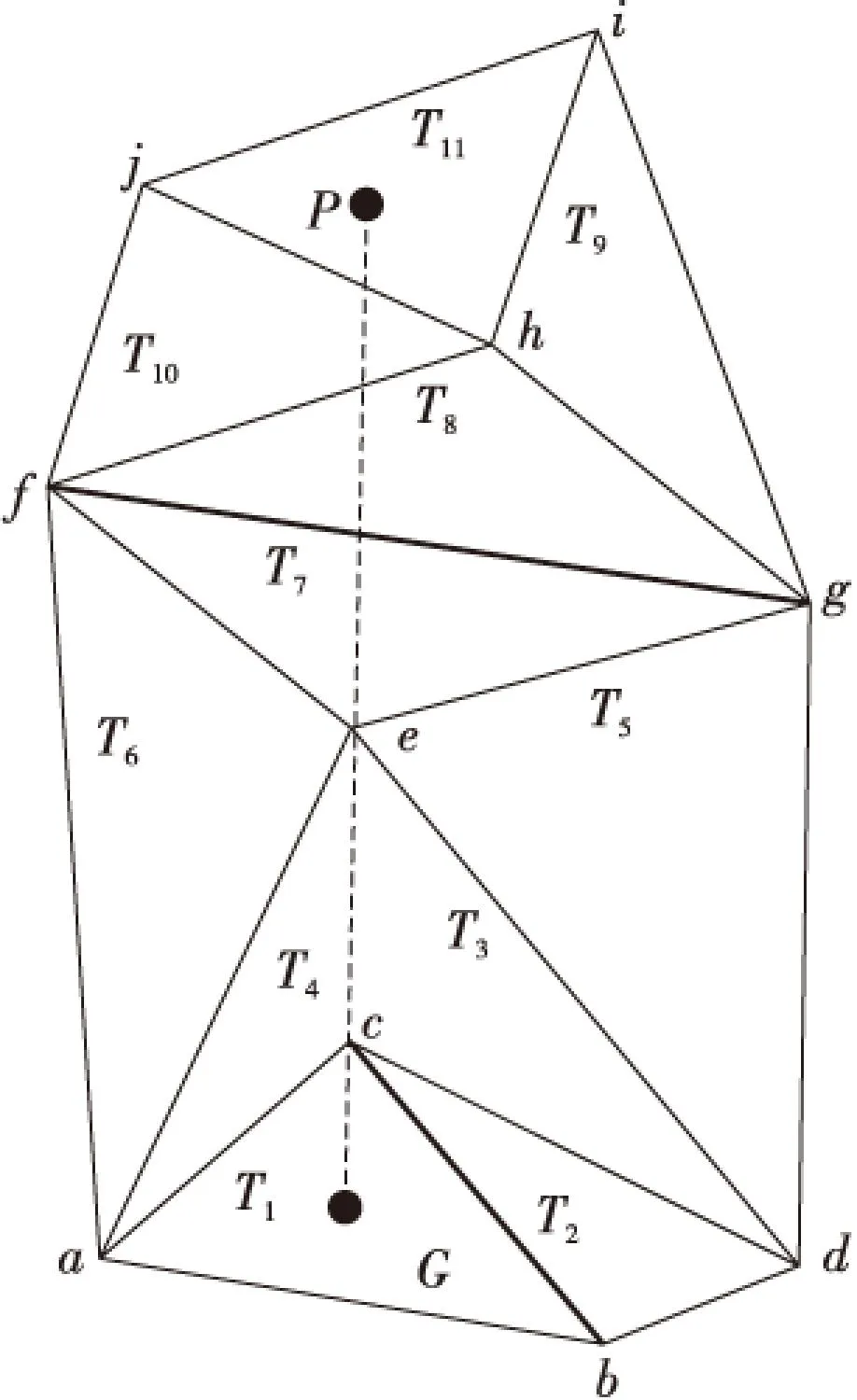
Figure 1　Best location path of the target triangle 图1　目标三角形的最佳定位路径

如图1所示，插入点为p，首三角形T1的重心为G，搜索方向线为pG，与三角形T1判断，pG和T1相交且交点为顶点c，则逆时针搜索c的对边，分别为〈b，d〉、〈d，e〉、〈e，a〉，判断pG和这些边是否相交，图中和〈d，e〉相交，交点仍为交点e，逆时针搜索e的对边〈d，g〉、〈g，f〉、〈f，a〉、〈a，e 〉，其中边〈g，f〉和方向线相交且交点不是顶点，且pG和边〈g，f〉的邻接三角形T8的交点个数为2，则搜索相交边〈f，h〉的邻接三角形T10，交点个数仍为2，则搜索T11，方向线pG和T11交点个数为1，则认为p处于T11中，目标三角形定位完成。上例中本文算法只进行了12次和三角形边的相交判断即完成了目标三角形定位，且搜索过程中基本按最短路径进行搜索，在速率上得到了较大提高。文中〈p，p0〉表示以p、p0为端点的边。

2.3.2Delaunay三角化

根据2.3.1节介绍的快速定位算法，实现平面的三角化。具体步骤如下：

步骤1增加三个附加点构造超级三角形作为初始三角形。

步骤2从平面点集中选择未处理的点p，利用上述的快速定位技术从三角形链表中选择包含p的目标三角形，连接p和三角形的三个顶点，删除原三角形，并根据Delaunay优化准则进行局部优化。

步骤3删除附加点的所有邻接三角形，生成二维Delaunay三角网格。

由于采样的随机性和采样精度等原因，可能会出现某点在三角形边上或者在局部优化过程中四点共圆，此时进行如下处理：

(1)若点在三角形的边e上，则和e的对点连接，与三角形的其它边形成三角形。

(2)若四点共圆，则不做处理，即不交换三角形对角线。

2.4网格拼接

将二维三角化结果反投影至三维空间并进行拼接，完成网格融合。

假设p1、p2∈S, 它们的最近点集分别为Nbhd(p1)和Nbhd(p2)，由它们生成的两张局部三角网为M1和M2。下面的任务是将它们整合成一张三角形网, 使得整个曲面在重建过程能以局部扩张的方式进行。

本方法先将M2中的所有三角形无条件地加入到M1中去, 然后判别并删除非法三角形。设pa为Nbhd(p2) 中的一点，记合并后pa的邻接三角形集为DT(pa) , 现在希望找出并删除DT(pa)中的非法三角形, 使得M1在pa处仍符合二维流形的定义。具体方法如下:

(1)如果pa的某一个邻接点pb关于pa的重数为3 或4, 则删去一个或两个拥有边〈pa，pb〉的三角形, 使得pb关于pa的重数为2, 且剩下的两个三角形不与DT(pa) 中的其它三角形关于pa重叠。

(2)当不存在重数为3 或4 的邻接点后, 如果DT(pa)中还有两个三角形关于pa重叠, 则删除其中一个三角形, 且使另一个三角形不再与DT(pa) 中的其它三角形关于pa重叠。

按上述过程对Nbhd(p2)中所有点进行操作，并更新点的邻接度，直至所有点都符合要求。

2.5漏洞检测

由于实际得到的点云数据总是存在噪声或采样不均匀等情况，导致重建后的曲面可能存在一些漏洞(这种情况很少)，需要对这些漏洞进行自动检测并处理。

根据重建后三角网格中的边信息，判断网络中是否存在边界边。若存在，则将边界边保存。在边界边中任取一边e，从边界边数组中搜索与e相连的边，直至这些边界边形成一个闭合回路，则停止搜索，进行下一个漏洞的检测。如图2所示中边界边有〈p1，p2〉、〈p2，p3〉、〈p3，p4〉、〈p4，p5〉、〈p5、p6〉、〈p6，p7〉、〈p7，p8〉、〈p8，p6〉，任选择一边〈p1，p2〉进行搜索，当搜索到〈p5，p6〉时，同时有两条边界边〈p6，p7〉、〈p6，p1〉与其相连，若选择〈p6，p7〉，则形成一个闭合回路{p1p2p3p4p5p6p7p8p6p1}；若选择〈p6，p1〉，则形成两个闭合回路{p1p2p3p4p5p6p1}和{p6p7p8p6}，这两者用下述方法进行漏洞弥补时效果是一样的，不用进行额外的判断。

在完成漏洞边界提取后，进行以下操作：如果漏洞的顶点个数为3，则直接将三点形成一个三角形加入三角网格；若顶点个数大于3，则任取回路上的一条边作为初始边，搜索与此边相连的两条边，分别计算这两边和初始边围成的夹角，取夹角最大的边和初始边形成三角形，并将新生成的边作为新的初始边重复上述过程。以图2为例，选取〈p1，p2〉作为初始边，并与其相连的两条边〈p2，p3〉、〈p1，p6〉分别计算∠p1p3p2和∠p2p6p1的大小，若∠p2p6p1大，则连接p2p6，使p1p2p6形成三角形加入网格，同时，p2p6代替p1p2形成新的边界边，持续上述过程，直至边界边数组为空。

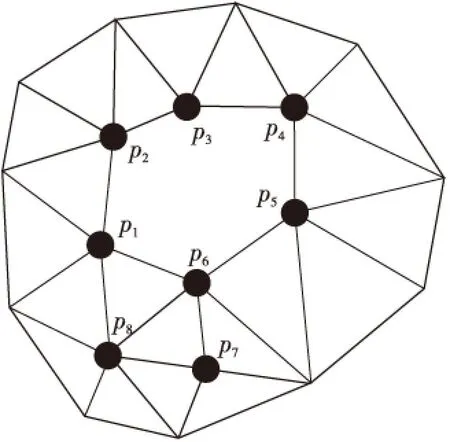
Figure 2　Holes testing 图2　漏洞检测

2.6算法整体框架

输入散乱数据点集合S={pi}，输出模型的三角网格M。算法整体实现框架如下：

步骤1置每个点为孤立点，根据每个点pi的k最近邻域Nbhd(pi)计算各个点的近似法矢量。

步骤2遍历集合S中的每个点，对边界点或者孤立点pi，删除Nbhd(pi)中的内点得到投影点的集合P，将P中点投影到pi所在的切平面上，且以pi的近似法向量为平面法向量。计算集合P时，可以设置阈值d，Nbhd(pi)中和pi欧氏距离小于d的点才能作为投影点，这可以在一定程度上降低噪声点对建模结果的影响。一般情况下，d=r*min(|pi,Nbhd(pi)|)，r为常数。

步骤3在切平面上利用2.3.2节介绍的Delaunay三角化方法进行快速三角化，并将结果投影至三维空间并得到局部三角网格Mi。

步骤4利用2.4节中介绍的网格拼接方法将Mi加入到M中，并用Delaunay优化准则进行局部优化。

步骤5集合S中的点遍历完成，得到一个比较完整的三维网格。

步骤6根据边信息检测是否存在漏洞，若有则进行漏洞弥补。

3实验结果与分析

本文算法已用C++在个人计算机上实现，并用人体膝关节等模型进行了测试(如图3～图5所示)。在实验中，k取10，运行时间测试结果见表1，时间单位为s。

Figure 3　Triangulation net generation of ACL of the knee using our algorithm 图3　本文算法生成的膝关节ACL三角网格

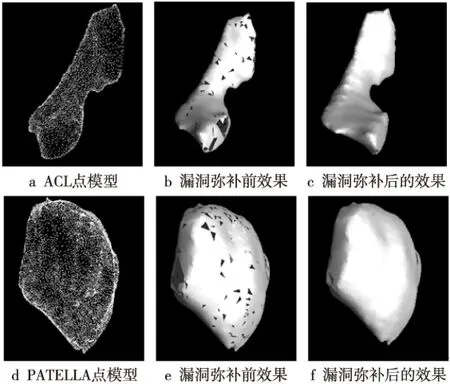
Figure 4　Comparison of reconstruction results of ACL and PATELLA 图4　膝关节ACL和PATELLA重建结果对比

Figure 5　Reconstruction results of other models 图5　其它模型重建的结果

由表1中实验结果可以看出，随着散乱数据点数量的增加，重建总耗时以趋于斜率为0.6的直线缓慢增加，避免了重建较大模型时时间消耗的几何倍数增加。在网格重建部分，本文算法明显快于文献[18]算法，而且随着模型规模的变大，本文算法在重建效率上的优势相对更加明显。这是因为文献[18]算法在切平面内进行Delaunay三角剖分时，首先将点进行预分类并在每个子类中进行排序，然后以最近生成的新三角形为首三角形，利用点和三角形三边关系进行三角形定位。通过分析可知，该算法不仅在分类、排序时浪费了一定的时间，而且选择的首三角形不一定是最适合的，并且利用点和三角形三边关系定位目标三角形时会出现搜索路径不唯一的情况，这进一步造成了时间的消耗。本文算法利用小四边形对首三角形搜索范围的限定和最小欧氏距离对首三角形的有效选择，使插入点在一般情况下至多判断两次便能确定目标三角形，而且利用插入点搜索方向线和三角形是否相交以及交点个数判断点和三角形的关系，在较大程度上提高了目标三角形的定位速度；而且本文算法能有效解决搜索路径不唯一情况，使定位路径最短或接近最短，这进一步提高了切平面内Delaunay三角剖分的速度。但是，切平面内进行三角化的采样点数量比较少，使本文的快速平面Delaunay三角化算法的优势得不到更加完美的展现。在漏洞检测及弥补阶段，避免文献[20]算法在提取漏洞边界时对边界环特殊情况的多余判断，而且利用凸壳边界的拼接技术直接对漏洞进行弥补，避免了在漏洞填充时文献[18]算法对新三角形的重叠判断和文献[20]算法对边界点的投影操作，在一定程度上提高了弥补速度。算法中漏洞边界的提取是漏洞处理阶段的主要耗时部分；另外，漏洞处理耗时和模型的大小无关，而和漏洞的多少、大小紧密相关；同时，边界边的存储顺序和存储方式在一定程度上影响漏洞边界的提取速度。

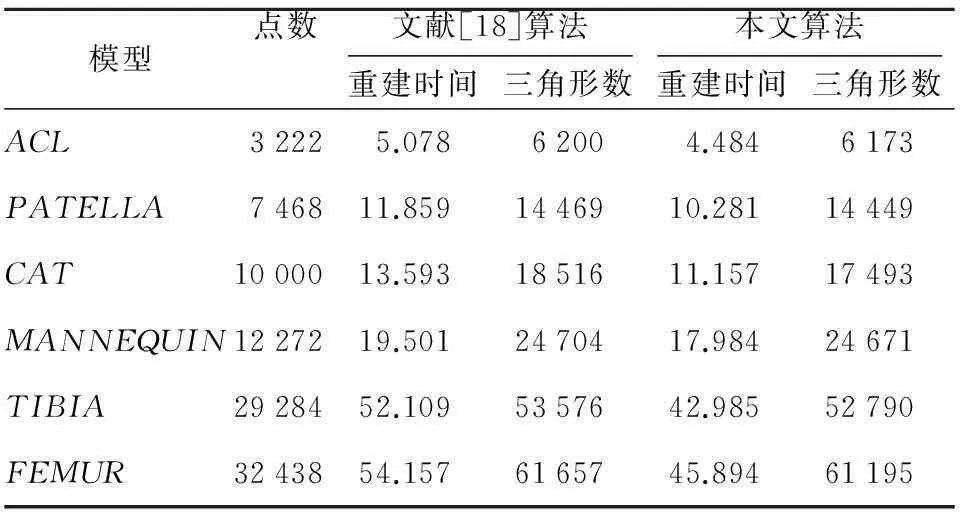
Table 1　 Comparison of running

4结束语

本文提出了一种新的平面Delaunay三角网中插入点目标三角形的快速定位算法，提高了切平面上的三角化速度；此外，本文还提出了一种新的漏洞弥补方法，借鉴多个凸壳边界的拼接思想完成漏洞弥补。实验表明了本算法的高效性和正确性。然而，由于采样的不均匀性以及模型的复杂性，算法还存在一些不足，例如本文算法中拓扑邻接点的确定是以假定几何邻接点就是拓扑邻接点为前提的，如何根据点之间的几何信息得到比较正确的拓扑信息是一个难点。真伪漏洞的鉴别也需要进一步研究，这将是未来要进一步解决的主要问题。

参考文献:

[1]HoppeH,DeRoseT,DuchampT,etal.Surfacereconstructionfromunorganizedpoints[J].CompterGraphics, 1992, 26(2):71-78.

[2]ZhouRu-rong,ZhangLi-yan,SuXu,etal.Algorithmicresearchonsurfacereconstructionfromdensescatteredpoints[J].JournalofSoftware, 2000, 12(2):249-255.(inChinese)

[3]FoleyTA.Visualizingandmodelingunstructureddata[J].TheVisualComputerInternationalJournalofComputerGraphics, 1993, 9(8):439-449.

[4]WendlandH.Piecewisepolynomial,positivedefiniteandcompactlysupportedradialfunctionsofminialdegree[J].AdvancesinComputationalMathematics, 1995, 14(4):389-396.

[5]MorseBS,YooTS,RheingansP,etal.Interpolationgimplicitsurfacefromscatteredsurfacedatausingcompactlysupportedraialbasisfunctions[C]//ProcofInternationalConferenceonShapeModeling, 2001:89-98.

[6]KojekineN,HagiwaraI,SavchenkoV.SoftwaretoolsusingCBRBFsforprocessingscattereddata[J].Computers&Graphics, 2003, 27(2):311-319.

[7]CarrJC,BeatsonRK,CherriJB,etal.Reconstructionandrepresentationof3Dobjectswithradialbasisfunctions[C]//ProcofSIGGR-APH’01, 2001:67-76.

[8]NielsonGM,HagenH,LeeK,etal.ImplicitfittingofpointclouddatausingradialHermitebasisfunctions[J].Computing, 2007, 79(2/3/4):301-307.

[9]DuXin-wei,YangXiao-ying,LiangXue-zhang.Amulti-scaleapproachto3Dscattereddatainterpolationbasedonradialbasisfunction[J].JournalofJilinUniversity(ScienceEdition), 2009, 47(5):1039-1041.(inChinese)

[10]DuXin-wei,YangXiao-ying,LiangXue-zhang.Implicitfittingofpointclouddataviaradialbasisfunctions[J].JournalofJilinUniversity(ScienceEdition), 2010, 48(2):157-162.(inChinese)

[11]FangLin-cong,WangGuo-zhao.Analgorithmofsurfacereconstructionbasedonradialbasisfunctions[J].JournalofZhejiangUniversity(EngineeringScience), 2010, 44(4):728-731.(inChinese)

[12]LawsonCL.Generationofatriangulargridwithapplicationtocontourplotting[M].California:JetPropulsionLaboratory,Pasadena, 1972.

[13]SibsonR.Locallyequiangulartriangulations[J].TheComputerJournal, 1978, 21(3):243-245.

[14]GreenPJ,SibsonR.Computingdirichlettessellationsinthelane[J].TheComputerJournal,1978,21(2):168-173.

[15]BowyerA.Computingdirichlettessellations[J].TheComputerJournal, 1981, 24(2):162-166.

[16]WatsonDF.Computingthen-dimensionalDelaunaytessellationwithapplicationtoVoronoipolytopes[J].TheComputerJournal, 1981, 24(2):167-172.

[17]TianJun-wei,ChenGang.AnimprovedDelaunaytriangulationalgorithm[J].JournalofXi’anTechnologicalUniversity, 2011, 31(4):334-338.(inChinese)

[18]WangQing,WangRong-qing,BaoHu-jun,etal.Afastprogressivealgorithmforunorganizedpoints[J].JournalofSoftware, 2000, 11(9):1221-1227.(inChinese)

[19]LiuShao-hua,WuDong-sheng,LuoXiao-long,etal.ResearchonalgorithmsofpointfastpositioninDelaunaytriangularnet[J].ScienceofSurveyingandMapping, 2007, 32(2):69-70.(inChinese)

[20]ZhangJian-qing,LiCai-lin,GuoBao-yun.Afastsurfacereconstructionalgorithmforunorganizedpointsontangentplaneprojection[J].GeomaticsandInformationScienceofWuhanUniversity, 2011, 36(7):757-762.(inChinese)

[21]WangShu-zhong,ZhangYou-sheng.Surfacereconstructionbasedonscatteredpointsets[J].ComputerScience, 2009, 36(5):269-272.(inChinese)

参考文献：附中文

[2]周儒荣, 张丽艳, 苏旭, 等. 海量散乱点的曲面重建算法研究[J]. 软件学报, 2000, 12(2):249-255.

[9]杜新伟, 杨孝英, 梁学章. 基于径向基函数的3D散乱点数据插值多尺度方法[J]. 吉林大学学报(理学版), 2009, 47(5):1039-1041.

[10]杜新伟, 杨孝英, 梁学章. 用径向基函数隐式拟合点云数据[J]. 吉林大学学报(理学版), 2010, 48(2):157-162.

[11]方林聪, 汪国昭. 基于径向基函数的曲面重建算法[J]. 浙江大学学报(工学版), 2010, 44(4):728-731.

[17]田军委，程钢. 改进Delaunay三角剖分算法[J]. 西安工业大学学报, 2011, 31(4):334-338.

[18]王青, 王融清, 鲍虎军, 等. 散乱数据点的增量快速曲面重建算法[J]. 软件学报, 2000, 11(9):1221-1227.

[19]刘少华, 吴东胜, 罗小龙, 等.Delaunay三角网中点目标快速定位算法研究[J]. 测绘科学, 2007, 32(2):69-70.

[20]张剑清, 李彩林, 郭宝云. 基于切平面投影的散乱数据点快速全面重建算法[J]. 武汉大学学报(信息科学版), 2011, 36(7):757-762.

[21]王树忠, 张佑生. 基于散乱点集的曲面重建[J]. 计算机科学, 2009, 36(5):269-272.