考虑公共自行车的城市公交出行路径优化方法和模型

考虑公共自行车的城市公交出行路径优化方法和模型*

江周1张存保1▲丁国飞2许志达2夏银霞1

(1.武汉理工大学智能交通系统研究中心武汉 430063；2.嘉兴市交通运输局浙江 嘉兴 314001)

摘要目前，城市公交出行路线优化时未考虑结合公共自行车的优点，使得现有的部分公交出行路径优化不够合理。针对这一情况，重点增加了对合理区域内步行、骑自行车换乘的考虑。分析公共自行车加公交出行路径优化的影响因素，并结合GIS建立公交(含公共自行车)数据模型，以换乘次数最少为优先目标，充分考虑合理区域内换乘的情况，起点和终点双向展开搜索，利用公交线路、公交站点集合求交集的方法查询出候选方案集。分别选取行程时间、乘车距离、步行距离较短的出行方案推荐给出行者。结合GIS系统利用该算法进行查询，将获得的优化方案与现有的优化方案进行比较，发现考虑自行车换乘的出行方案平均出行时间减少15.8%，平均出行距离减少18.7%，平均出行费用减少32.3%。

关键词路径优化；公交出行；自行车换乘；GIS系统

中图分类号：U491.4文献标志码：A

收稿日期：2014-09-25修回日期：2014-12-31

基金项目*国家自然科学(批准号：51108361)、中央高校基本科研业务费专项资金项目(批准号：2014-IV-138)、浙江省交通运输厅科技计划项目(批准号：2012T21)资助

作者简介：第一江周(1988-),硕士研究生.研究方向:交通信息工程及控制.E-mail:15827227641@163.com

通讯作者：▲张存保(1976-)，博士，副研究员.研究方向：交通信息工程及控制.E-mail:zhangcunbao@163.com

An Optimization Model of Public Transportation Routes

considering Public-sponsored Bicycles

JIANG ZhouZHANG CunbaoDING GuofeiXU ZhidaXIA Yinxia

(1.IntelligentTransportSystemResearchCenter,

WuhanUniversityofTechnology,Wuhan430063,China；

2.Jiaxingcitytransportdepartment,Jiaxing314001,China)

Abstract:At present, the advantages of using public-sponsored bicycles have not been considered in the process of optimizing the routes of public transit, therefore the routes used may not be optimal. Due to this, transfer through walking and riding a bike in a reasonable area is considered. Firstly, the factors that should be considered when optimizing service routes under the assumption that both public-sponsored bicycle and bus are available, are analyzed. Travel route data(including public bicycles) is collected and then set up within a GIS environment. Using the minimal number of transfer as the target, the transfer within a reasonable distance is fully considered, and the search at each side of original and destination is explored. The candidate routes are enumerated using the joint locations of bus lines stations. Then those routes with minimal travel time, travel distance and/or walking distance will be recommended to travelers. Finally, the algorithm developed is used to query the optimal routes within a GIS system,and the results show that in consideration of bike transfer the average travel time is reduced by 15.8%, the average trip distance is reduced by18.7% and the average travel expense is reduced by 32.3%, compared with the existing optimization scheme.

Key words:path optimization; bus travel; bicycle ride; GIS system

0引言

随着城市快速地发展, 城市的发展规模日益扩大，为了满足人们出行的需要, 城市公共交通覆盖的范围越来越广, 公交线路也逐渐增多。公交车为人们的出行带来了极大的便利, 但是由于公交线路很多, 给人们在选择乘车线路时带来了一定的困扰。因此, 为市民提供方便、快捷、高效的公交出行线路, 不仅有助于他们的出行, 同时可以减少不必要的交通流量，有利于城市交通运输效率的提高。

目前，国内外许多学者对城市公交出行路线优化问题进行了广泛的研究。K.Hong 等[1]利用遗传算法解决了公交方式换乘过程中计算换乘数目及换乘费用等问题；A.Lozano等[2]对公交出行最优路径方式中的行为问题进行了研究，提出公交出行路径优化算法；侯刚等[3]通过分析乘客出行心理，提出以换乘次数最少为优先目标，重点考虑公交站点的空间关系，提出由空间数据到拓扑模型再到搜索模型的公交网络双层建模方案；唐炉亮等[4]根据城市道路功能等级与出租车的通行频率等信息素，建立出租车驾驶人路径选择信息素等级路网，综合考虑路径通行时间、通行距离、路径信息素等级等多个因素，提出了基于蚁群优化算法的公众出行路径规划优化算法；符光梅[5]针对公交网络二维模型的社团结构特性，结合人们的实际出行需求，提出了基于二维模型的公交多路径搜索算法。以上研究解决了最优路线求解问题，但是仍然存在一些其他问题：例如当公交站点间的间距较小时，步行换乘的距离在出行者可接受范围内，上述部分算法由于行车路线方向不同，相关路线间没有交叉点而遗漏了这些合理换乘的方案；还有的算法虽然解决了以上问题，却没有在最优目标中考虑步行距离、乘车距离等约束条件。

据调查，我国城市交通出行距离为3 km以下的占很高比例，在这一出行范围内公共自行车有其他许多交通工具不具备的优势[6]。与其他出行方式相比，自行车具有环保节能、自主灵活、出行费用低、连续便捷以及运行的可达性强等优势；而城市公交车的优势则是快速、舒适、运载量大，但其可达性和灵活性较差。分析可知，公共自行车可以弥足公交车的不足之处。公共自行车的出

现，不仅能有效解决“公交出行最后1 km问题”以及“城市交通两难问题”，而且可以优化一些不合理的出行方案[7]。因此，考虑到自行车和公交车的特点具有互补性，在进行公交出行路径优化时，考虑自行车换乘是很有必要的。

1公共自行车+公交出行线路优化的影响因素及总体思路

当出行者选择公交车出行时，一般有多个可行的乘车方案，出行者往往需要根据实际情况做出选择。对于出行者来说，选择乘车路线时有很多因素需要考虑，如换乘次数、行程时间、所需费用等，不能简单地概括为最短路问题[8]。既有研究表明，大多数出行者以换乘次数最少为优先考虑目标[9]，公交网络的设计也以平均换乘次数最少为重要目标[10]。因此，笔者选择换乘次数最小(自行车换乘、公交换乘都算1次换乘)为最优目标。旅行费用的计算方式较多，但所需费用一般与距离正相关，为避免过于复杂，选择乘车距离最短为次优目标。另外，由于不同的人选择线路考虑的因素不同，根据实际需要分别考虑步行距离、行程时间作为次优目标，根据不同的次优目标推荐最优路径。即在可行换乘方案中选择换乘次数最少，且在满足此条件下分别使乘车距离最短、步行距离最短、行程时间最短的各路径为最优路径。

综上分析，考虑公共自行车换乘的公交出行路线优化问题可抽象为这样的模型：设给定起始站点v0，终止站点vd，可行的公交线路集合为TR={ TRi| TRi=(v0，ri1，vi2，…，vd)}。TRi为在起点v0选择公交线路ri1到达站点vi1，再换乘线路ri2到达站点vi2，……，最终到达终止站点vd。该路径换乘数为Ni，乘车距离为Si，出行者的目标函数为Ni最小，当Ni相同时，分别选择乘车距离Si较短、步行和骑行距离Li较短、行程时间Ti较短的线路作为最优路径。基于此模型，首先利用GIS建立公交(含公共自行车)数据模型，存储公交站点、公交线路、自行车网点等信息；然后根据调查获得的大多数人在采用公共自行车加公交车出行时选择线路的方法，利用SQL查询技术设计搜索算法，通过公交站点集合求交集、公交线路集合求交集、搜索邻近自行车网点、邻近公交站点获得多条最优出行线路，按步行距离、乘车距离、行程时间的长短依次排序并推荐给出行者。

2公交(含公共自行车)数据模型的GIS表达

在公交出行查询系统中，参照城市道路网建立的公交(含公共自行车)数据库是整个查询系统的数据基础。公交实体数据的表达是否适当对于公交数据库的使用效率将产生直接影响，合理的数据结构有助于减少搜索次数，提高搜索效率。针对城市公交车数量大、公交线路复杂等情况，重点考虑换乘算法的效率，笔者提出1种基于空间数据和属性数据的公交(含公共自行车)数据模型。该模型以Geodatabase数据模型存储所有的公交站点、自行车网点等空间数据，以关系数据库的形式存储公交线路、站点与线路之间的关系等信息，通过关键字段关联空间数据和属性数据来表达复杂的公交网络结构。

公交站点(bus stop)数据库主要存储每个公交站点的编号、名称和坐标等信息，它对应着1个矢量点状要素图层，其数据结构见表1。其中：Stop ID字段用于区分同名站点，解决合理范围内步行换乘问题。所谓的同名站点是指名称相同或相似并且空间位置相近的站点，例如,世纪广场东站、世纪广场北站。处理数据时，2个公交站点相隔的距离设为L，同名站点间的距离阈值设为L阈值，根据乘车的实际情况，距离阈值L阈值取为200 m。利用GIS的分析功能将d≤L阈值的站点合并为同名站点，赋予相同的Stop ID值。Near Point ID用于存储公交站点附近的公共自行车网点编号，根据实际情况，取r=500 m。

表1　公交站点数据结构

公交路段(bus route)数据库主要存储相邻且有直达公交车的2个公交站点间的路段信息，其数据结构见表2。对于任意1个路段，当往返的行车线路相同时，则存储1个要素；若不相同，则按照起止点顺序的不同分别存储。因此，包含该路段的所有公交线路均可共享该路段信息，有助于减少冗余的数据。

公交线路(bus line)属性表存储城市所有公交线路的信息，包括线路编号、线路名称、票价、开车线路站点(line stop)关系表主要存储每条公交线路所经过的公交站点编号以及每个公交站点在其上行线路、下行线路中的序号等信息。该表存储公交换乘查询系统的核心信息，其数据结构见表4。表4中:Seq Up,SeqDown分别表示站点在上行线路、下行线路中的序号，0表示该线路不经过此站点; Route ID Up,Route ID Down则分别记录公交站点与上行线路、下行线路中相邻的下1个公交站点间的路段编号，若不存在相邻的下一站点, 则该值为空。

表2　公交路段数据结构

时间段等内容，其数据结构见表3。考虑到实际情况下，少数公交线路往返所经过的公交站点不同，每条公交线路都标识为上行线路和下行线路。

表3　公交线路数据结构

现以编号为1的公交线路(见图1)为例简述查找方法。1号公交线路数据信息存储结构见表4，其上行线路所经过的公交站点编号(seq up)为: 1—2—3—4—6，相应的公交路段编号(Route ID Up)为: 01—03—04—05；下行线路经过的公交站点编号(seq down)为: 6—5—3—2—1，对应的路段编号(route ID down)为: 10—08—03—02。利用站点编号可以获得公交站点的名称，利用路段编号可以获得公交上下行线路的信息，因而对上行、下行线路可加以区分。

表4　线路站点数据结构

图1　1号公交线路示意图

自行车网点(bike point )数据库主要存储每1个公共自行车网点的编号、名称、坐标以及邻近自行车网点编号、邻近公交站点编号、自行车网点状态等信息。其中自行车网点状态是指该网点可借车辆数，可还车辆数。邻近自行车网点是指以该网点为中心，半径为2 500 m(骑自行车出行距离的阈值)范围内的自行车网点。邻近公交站点是以该网点为中心半径为500 m范围内的公交站点。该图层的数据结构见表5。

表5　自行车网点数据结构

3公共自行车+公交出行路径优化算法

采用公共自行车进行换乘的主要原因是短距离内将作为步行、公交、出租车的替代方式[11]。据相关统计表明，公众出行采用公共自行车出行的平均时耗约为15 min，平均骑行距离小于2.5 km[12]。考虑到出发地和目的地的名称不一定是公交站点的名称，因此需要结合GPS系统将出发地、目的地的位置快速关联到附近的公交站点、自行车网点，再利用搜索算法获得出行方案。基于上述考虑，设计的公交(含公共自行车)出行最优路径搜索算法如下。

1) 输入起始点A和目的点B，利用GPS系统搜索附近(半径r=500 m的范围)的公交站点、自行车网点，并计算A、B间的距离dAB。

2) 若dAB小于500 m，则将步行的出行方式推荐给出行者，结束运算。

3) 若dAB小于2 500 m，且A、B均为自行车网点，则考虑采用骑自行车的方式直接从A点骑到B点，结束运算。

4) 若A，B不均为自行车网点，但在A和B半径为500 m的范围内存在自行车网点，则考虑采用步行、骑自行车的组合方式出行，结束运算。

5) 设VA，VB分别为A、B在半径为500 m范围内公交站点的集合，对公交站点集合VA中的任一站点vi(i=1,2,…)、集合VB中的任一站点vj(j=1,2,…)，在线路站点关系中搜索经过起始站点vi的线路集合Roi以及经过目标站点vj的线路集合Rdj。

6) 判断是否有Roi∩Rdj≠∅，若有1条线路满足要求，则该公交线路即为最优线路。若有几条线路满足要求，则考虑次优化目标

7) 分别对线路集合R0i,Rdj中的每条线路搜索其经过的所有站点，这些站点分别组成了集合V0i，Vdj。

8) 判断是否有V0i∩Vdj≠∅，若有1个站点vk(k=1,2,…)满足要求，则该站点为1次换乘的站点。若有多个站点符合条件，则分别求出每1个站点作为换乘点时该线路的出行距离、行程时间，按照距离长短、时间长短依次推荐给出行者。若考虑骑自行车，则利用GIS系统查找离起点A较近的自行车网点集BA(步行)，对BA中任意BAi，从Bike Point查找BAi点邻近的自行车网点Bj(骑行)，再查从Bj点(步行到邻近公交站点)到终点B附近公交站点的公交线路。同理，查找离终点B较近的自行车网点集BB，再搜索BBi点的邻近自行车网点Bk到A点附近公交站点的直达公交车，比较各种出行方案，按步行距离长短推荐路径结束运算。

9) 在Line Stop表中搜索通过集合Voi以及Vdj的所有不同线路, 形成线路集合Ri1和Rj2；设Rm= Ri1∩Rj2。

10) 判断是否有Rm≠∅。若Rm不为空集，则存在二次换乘方案。搜索集合Rm中每条线路所经过的站点, 组成中间换乘站点集合 Vm。设Vc1=Vm∩V0i，则 Vc1为第一换乘点集合；设Vc2=Vm∩Vd，则Vc2为第二换乘点集合。分别求出集合Vc1，Vc2中各点作为换乘点的距离、行程时间，按照距离长短、时间长短依次推荐给出行者。若考虑骑自行车，则利用GIS搜索起点A附近的自行车网点集BA(步行)，对BA中任意元素BAi，从Bike Point搜索BAi点邻近自行车网点Bj(骑行)，然后从Bike Point查Bj点邻近公交站点E(站点E为1次换乘点)，查出E点能直达的所有站点的集合VE，则VE与Vdj的交集即为第二换乘点的集合。同理，反过来利用GIS搜索B点附近自行车网点集BB，再搜索BBi的邻近自行车网点F及其邻近公交站点G(站点G为第二换乘点)，则VG与V0的交集即为第一换乘点的集合。并分别搜索V0i，Vdj附近存在自行车站点C、D，且C、D距离小于2 000 m，则从A点步行到vi，再乘公交到C点，然后骑自行车到D点，最后坐车到vj点并步行至B点。并搜索A点、B点附近的自行车网点集BA、BB(步行)，然后搜索BAi点、BBi点邻近自行车网点E、F(骑行)，再确定E、F邻近公交站点间的直达车。最后比较各种方案里的步行距离(若步行距离相同，再比较骑行距离)，按距离的长短将各路径输出并推荐给出行者，结束运算。

11) 若上述步骤没有搜索到满足要求的公交线路，则输出“没有找到换乘次数不超过2次的乘车线路”，结束运算。

上述公交出行路径优化算法不仅解决了合理区域内步行换乘的问题，而且首次考虑利用公共自行车进行出行路径优化、符合未来城市交通发展的需要。该算法全面分析了公交加公共自行车出行可能出现的情形，包括骑车、骑车+乘车、乘车+骑车、骑车+乘车+乘车、乘车+骑车+乘车、乘车+乘车+骑车、骑车+乘车+骑车等。基于该算法的整个搜索过程平均花费时间不超过0.26 s，能够满足现实应用的需要，其搜索过程如图2所示：

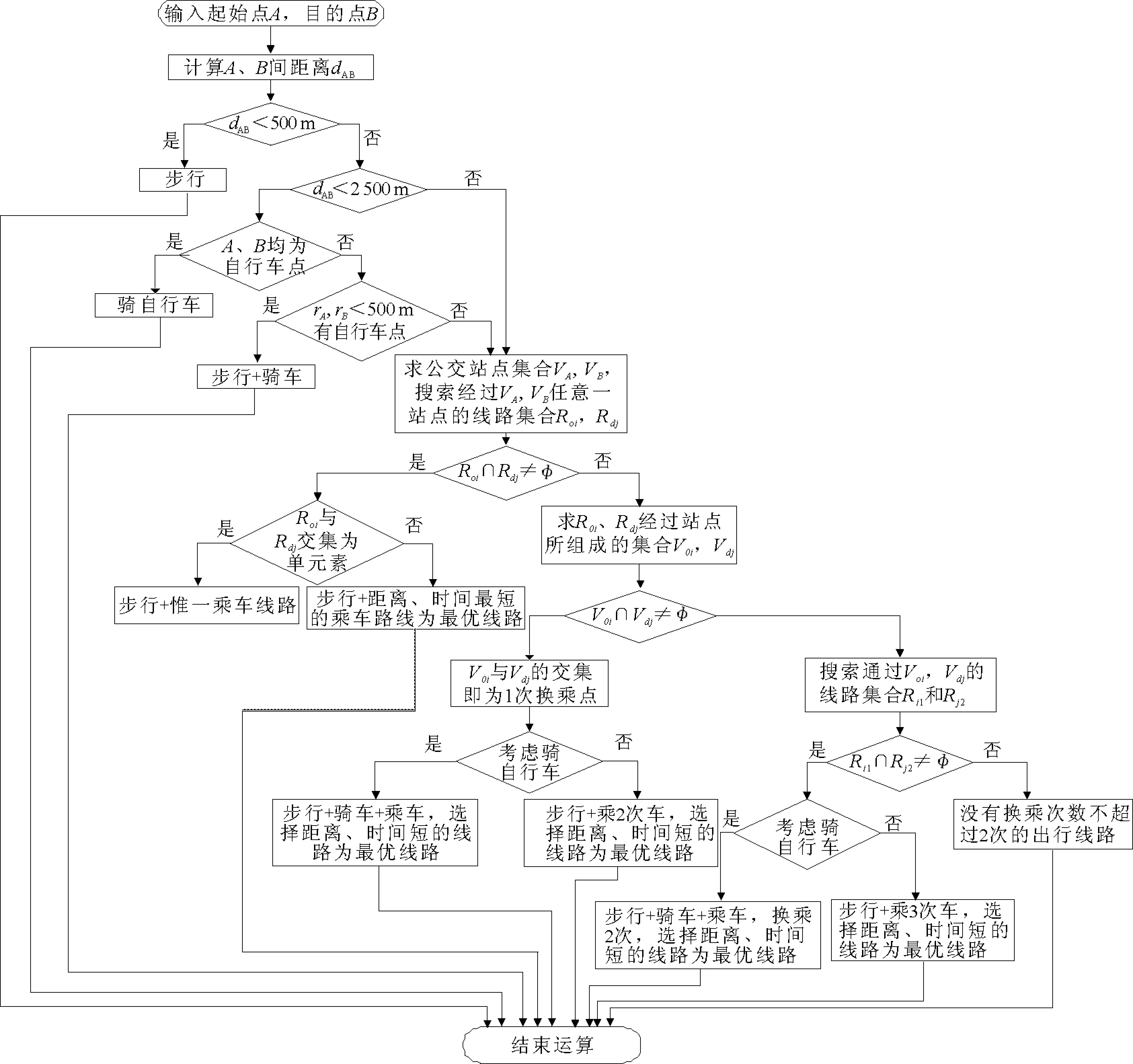
图2　公共自行车+公交出行路径优化算法流程图

4实例验证

根据公交网络、公共自行车网络的特点，利用可视化编程工具对GIS系统进行二次开发。

利用上述出行路径优化方法，通过参与研制的嘉兴市智慧公交查询系统，输入起点和终点，可获得以换乘次数最少为最优目标，乘车距离、步行距离、行程时间最短为次优先目标的3种出行方案。例如输入起点博物馆，终点汇金广场，利用公交查询系统可获得多条优化路线，具体线路见图3、图4所示。其中，未考虑公共自行车换乘的出行方案用时32 min,行程距离3 350 m，而考虑换乘的出行方案用时12 min，行程距离为2 100 m。对比发现，考虑公共自行车换乘的出行线路用时较少，行程距离较短，费用较低。

图3　未考虑公共自行车换乘的公交出行方案

图4　考虑公共自行车换乘的公交出行方案

为了更加全面地比较2种公交出行方式(考虑自行车换乘和未考虑自行车换乘)，根据嘉兴市OD交通数据选取了560组不同的起讫点，包括短程、中程和远程，基本上能够反映嘉兴市出行需求特征。输入不同的起讫点获得2种出行方式下的出行方案，统计每组起讫点最优出行方案的时间、距离、费用，计算得到两种出行方式下的平均数据，结果如表6所示。

观察结果可知，考虑公共自行车换乘的出行方式下其平均行程时间、距离及费用均较小。究其原因，平均行程时间减少是由于省去了乘公交等待的时间、出行距离较短以及高峰时骑车的平均速度较快；平均行程距离减少是因为行程路线相对较直、减少了不必要的弯路；平均出行费用减少是因为可以免费使用公共自行车(1 h以内)。因此，综合比较各种因素，考虑公共自行车换乘的出行优化方案更合理，更能满足嘉兴市居民的出行需求。

表6　两种出行方式下的平均数据

5结束语

分析发现自行车和公交车的特点具有较强的互补性，在进行公交出行路径优化时考虑公共自行车换乘是十分必要的。选取换乘次数最少为最优目标，分别以乘车距离、步行距离、行程时间较短为次优目标，创建数据库，起讫2点双向展开搜索，通过SQL查询，利用集合求交集的方法获得出行方案。该算法不仅解决了在不同站点间步行换乘的问题，而且也解决了结合公共自行车进行换乘的问题。另外，该算法区分上下行线路，计算速度快，能够为出行者提供多种不同的出行方案，最大程度地方便出行者的出行。由于实际生活中公交出行比较复杂，还有许多因素需要考虑，如行程时间的精确度、换乘点的便利性等因素，都需要进行更加深入的研究。

参考文献

[1] LozanoA,Storchi G.Shortest viable path algorithm in multimodal network [J]. Transportation Research Part A, 2005,35(5):225-241.

[2]Hong K C W,Yip K H.Modeling transfer and non-linear fare structure in multi-modal network [J]. Transportation Research Part B. 2007,37(6):149-170.

[3]侯刚，周宽久.基于换乘次数最少的公交网络最优路径模型研究[J].计算机技术与发展，2008,18(1):44-47.

HOU Gang,ZHOU Kuanjiu.Research for public traffic network model of optimum route with minimal transfer times[J].Computer Technology and Development,2008,18(1):44-47.( in Chinese).

[4]唐炉亮,常晓猛,李清泉,等.基于蚁群优化算法与出租车GPS数据的公众出行路径优化[J].中国公路学报，2011,24(2):89-95.

TANG Luliang,CHANG Xiaomeng,LI Qingquan,et al.Public travel route optimization based on ant colony optimization algorithm and taxi GPS data[J].China Journal of Highway and Transport,2011,24(2):89-95.( in Chinese).

[5]符光梅.基于二维模型的公交网络优化及出行方案研究[D].济南:山东师范大学,2013.

Fu Guangmei. Public transportation network optimization based on two-dimensional model and travel program research[D].Jinan: Shandong Normal University,2013.( in Chinese).

[6]常磊，刘仁义，张丰,等.考虑多方式换乘的公交网络最优路径算法[J].浙江大学学报，2011,38(6):701-707.

CHANG Lei,LIU Renyi,ZHANG Feng,et al.The optimal path algorithm of bus network considered multi-mode transferring[J].Journal of Zhejiang University, 2011,38(6):701 -707. ( in Chinese).

[7]叶丽霞.城市公共自行车调度系统研究[D].南京:南京理工大学，2013.

YE Lixia.Research of city public bicycle transfer system[D].Nanjing: Nanjing University of Science and Technology,2013.( in Chinese).

[8]李丹，黄正东.顾及换乘距离的城市公交系统出行路径优化研究[J].交通运输工程与信息学报,2008,6(4):110-117.

LI Dan,HUANG Zhengdong.Optimizing urban transit travel routes with special considera-tion of transfer distance[J].Journal of Transportation Engineering and Information,2008,6(4):110-117.( in Chinese).

[9]左毅刚,李文权,陈茜,等.公交信息条件下的公交出行意愿研究[J].交通信息与安全，2014,32(2):57-62.

ZUO Yigang, LI Wenquan, CHEN Qian, et al. Bus travel willingness under the condition of bus information[J].Journal of Transport Information and Safety, 2013, 32(2):57-62. ( in Chinese).

[10] 周道清.公共交通换乘算法研究及查询系统实现[D].成都:四川师范大学, 2012.

ZHOU Daoqing.The research of transfer algorithm and the implementation of inquiry system for public traffic network[D].Chengdu: Sichuan Normal University,2012.( in Chinese).

[11]李配配,崔珩.公共自行车与轨道交通的接驳与换乘研究[J].交通科技,2013,18(1):154-157.

LI Peipei,CUI Heng. Study on connection and transfer system of public bike and rail traffic[J].Transportation Science and Technology,2013,18(1):154-157.( in Chinese).

[12]朱玮,庞宇琦,王德,等.公共自行车系统影响下居民出行的变化与机制研究[J].城市规划学刊,2012,15(6):76-81.

ZHU Wei,PANG Yuqi,WANG De,et al.Travel behavior change after the introduction of public bicycle system[J].Urban Planning Forum,2012,15(6):76-81.( in Chinese).