锯齿形拖拽体的沙泳运动离散元模拟研究

锯齿形拖拽体的沙泳运动离散元模拟研究

郭鸿1,2，陈茜1，李军1，骆亚生2，胡海军2

(1.陕西理工学院 土木工程与建筑学院， 陕西 汉中 723000；2.西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100)

[摘要]为了探索锯齿形拖拽体在颗粒中平动运动时所受阻力和升力的变化规律，利用颗粒离散元数值模拟的方法，对不同的锯齿倾角、侵入深度、运动速度以及边界条件情况下的拖拽体进行了比较全面的分析研究。结果表明，锯齿倾角越大，阻力和升力越大，侵入深度越大和速度越大，阻力越大。最后，建立了拖拽阻力的建议公式，实际归一化结果表明，锯齿倾角一定时，就可以确定相应参数，进而表达不同拖拽速度和不同侵入深度时的拖拽阻力。

[关键词]颗粒流；沙泳；拖拽阻力和升力

[文章编号]1673-2944(2015)05-0036-05

[中图分类号]TU443

收稿日期：2015-03-15

基金项目：国家自然科学基金资助项目(51178392，51409220)；陕西省教育厅科学研究计划项目(15JK1117)

作者简介：郭鸿(1984—)，男，陕西省长武县人，陕西理工学院讲师，博士，主要研究方向为岩土力学离散元数字模拟。

全侵入型拖拽体在颗粒中的运动叫作沙泳，其运动情况十分复杂。在平动运动情况下，阻力和升力是重点考虑的问题。全侵入型拖拽问题中最典型的属于沙泳问题。由于沙泳问题的复杂性，近年来引起了广大研究者的重视[1-3]。沙泳问题的应用范围十分广阔：在物理领域内，纯力学作用机制需要深入研究[4-7]；在生物学领域，沙漠生物的运动以及仿生学对其要求也比较迫切[8]；在农业领域，机械和土壤的相互力学作用为设计和改进农业机械也起到理论指导作用[9-10]；在岩土地质领域，挖掘，采矿等[11]方面的应用和实践也非常普遍。全拖拽体在颗粒中游动的过程中，除了涉及到水平方向的拖拽阻力以外，还受到非常明显的竖直方向的升力。不同拖拽体形状所受的力都不同。尽管在全侵入型拖拽体方面有较多的研究，然而，由于其研究对象几何形体比较复杂，很难得出比较普遍的结论。比如，对于其他因素诸如侵入深度和拖拽速度对拖拽阻力的定量影响、非竖直拖拽体情况下浮力和升力的关系等还缺少系统的研究。另外，对于更为复杂的拖拽体(比如锯齿形)，目前为止作者还未发现相关的研究成果。

因此，本文以全侵入锯齿形拖拽体为研究对象，全面分析了拖拽速度、侵入深度、锯齿倾角以及运动方向等因素对拖拽阻力和升力的影响。在此基础上，初步建立了拖拽阻力和升力的半经验模型。以期为颗粒流拖拽问题的理论和实践提供参考。需要指出的是，由于在工业过程中，拖拽基本上发生在有限容器内，故本文着重考虑非周期边界的运动规律，同时也分析周期边界和非周期边界的异同。

1离散元数值实验

锯齿形拖拽体的离散元模型见图1(a)。入侵深度从颗粒的自由表面到拖拽体的底部，表示为Z，拖拽体的长度和高度分别表示为D和T，拖拽体的锯齿斜面和水平方向的夹角为θ。图1(b)和(c)分别代表锯齿拖拽体的初态和终态。需要说明的是，本文研究的是拖拽体顺齿运动的情况(拖拽体向右运动)。可以看出，全侵入拖拽体的堆积效应也十分明显。

(a) 几何模型　　　　　　　　　　　　(b) 初始状态　　　　　　　　　　(c) 终态 图1　锯齿形拖拽体的运动初态和终态示意图

全侵入型拖拽体的离散元数值几何参数描述如下：容器高度取0.3 m，宽度0.6 m，拖拽体的侵入深度采用0.05 m，0.15 m和0.25 m，拖拽速度取0.02 m/s，0.1 m/s和0.2 m/s，拖拽体宽度D为6.2 cm，厚度T为1.2 cm。离散元颗粒的细观参数如表1所示。

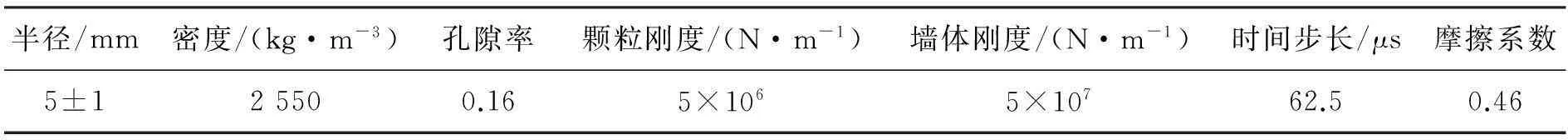
表1　离散元模拟物理参数表

2数值实验结果

2.1　速度影响规律

以侵入深度Z=0.15 m，锯齿倾角θ=15°为例，得到拖拽速度对拖拽阻力的影响如图2所示。可以看出，对于顺齿方向来说，初始状态时的拖拽阻力均比较大，然后随着拖拽体运动的稳定，拖拽阻力随之稳定。这和竖直形拖拽体[11]初始拖拽阻力比较小的现象不同，其原因是锯齿形拖拽体由于其形状的特殊性，导致初始状态的阻力增大。然而，本文和实际情况的不同在于，本文的拖拽体全程都是匀速运动，实际情况应该是初始速度为零，然后速度逐渐增加。加之速度对拖拽阻力的影响规律，不难设想，如果实际的运动速度是从零开始，那么初始拖拽阻力也一定是比较小。需要说明的是，关于锯齿形拖拽体在非匀速运动状态下拖拽阻力的变化规律，本文暂不涉及。

2.2　侵入深度影响规律

以锯齿倾角θ=30°，拖拽速度v=0.2 m/s为例，侵入深度采用Z=0.05 m、0.15 m和0.25 m，如图3所示。侵入深度对拖拽阻力的影响十分显著，拖拽阻力随侵入深度的增大而增大。顺齿形拖拽体的阻力曲线比较平滑。

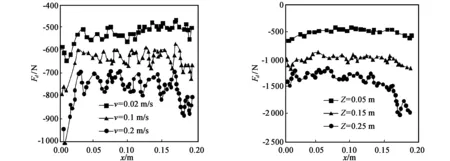
　　　图2　 速度对锯齿形拖拽体拖拽阻力的影响(θ=15°)　　　　　　　图3　 深度对锯齿形拖拽体拖拽阻力的影响(θ=30°)

2.3　锯齿倾角影响规律

以v=0.2 m/s，Z=0.25 m为例，分析锯齿倾角对拖拽阻力(图4(a))和升力(图4(b))的影响规律。将矩形拖拽体看成倾角为零的锯齿形拖拽体。可以看出，整体规律是在顺齿运动状态时，拖拽阻力或者升力随着锯齿倾角的增大而增大，但是当锯齿倾角增大到30°时，无论是阻力还是升力都基本不随倾角变化。另外，锯齿倾角在15°以下和30°以上时的拖拽阻力出现明显的分化现象，且低倾角时阻力较小，高倾角时阻力较大，这就说明倾角对阻力的影响不是简单的单调递增关系；倾角对升力的影响和对阻力的影响不同，随着锯齿倾角的增大，升力增大越来越缓慢，说明倾角对增大的作用是有限的。

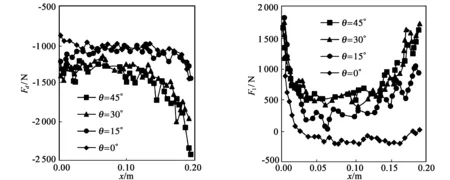
(a) 阻力　　　　　　　　　　　　　　　　　　　　(b) 升力 图4　θ对拖拽阻力和升力的影响

2.4　边界条件影响规律

全侵入拖拽体在拖拽阻力和升力方面都存在非常明显的边界效应。在DEM中，通过设置周期边界的方法，将颗粒床转化成半无限离散介质体。以θ=0，v=0.2 m/s，Z=0.25 m为例，对于顺齿方向的拖拽阻力(如图5(a)示)，周期边界条件下的数值波动更小，且几乎不存在终态边界效应的现象；对于顺齿方向的升力(如图5(b)示)，周期边界条件下的数值略大，这是因为此时颗粒床表面的颗粒堆积较弱，导致有效的侵入深度较小，因此升力较非周期边界情况的略大。这是由于非周期边界对拖拽体有非常显著的约束作用，这种约束促使颗粒对拖拽体产生很强的反作用力。而周期边界相当于半无限体，左右边界几乎无任何约束，颗粒流动很顺畅，因此波动就很小。

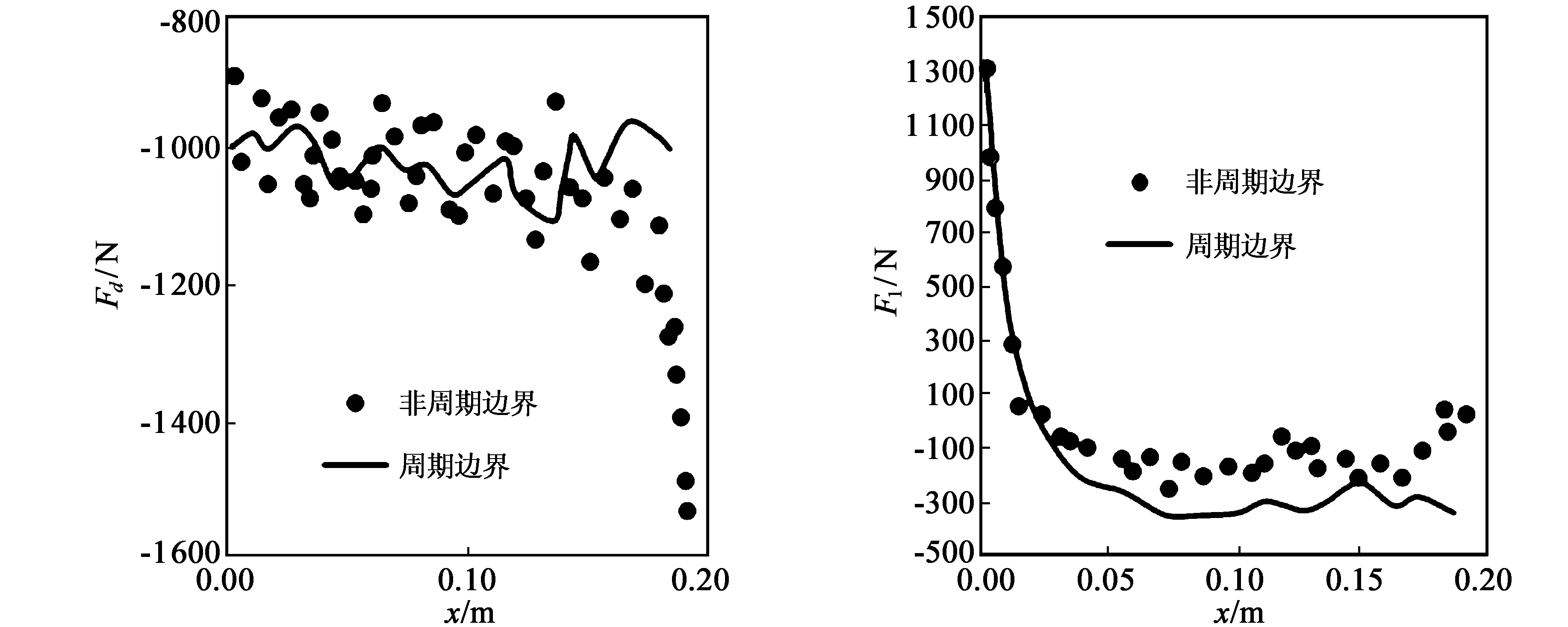
(a) 阻力　　　　　　　　　　　　　　　　　　　(b) 升力 图5　全侵入拖拽体的边界效应现象

3拖拽阻力预测公式

由上文的分析可知，拖拽速度和侵入深度对阻力的影响非常明显。基本规律是阻力和拖拽速度是线性关系。设速度影响项为v+av，av是速度影响参数。同时，拖拽阻力和侵入深度也是线性关系，设样侵入深度影响项为Z+az，az是侵入深度影响参数。从而得出全侵入锯齿形拖拽体的拖拽阻力的表达式为：

(1)

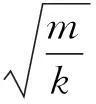
将不同锯齿倾角的拖拽体在不同速度和侵入深度时的拖拽阻力用式(1)归一化，得到的位移和Cp值的关系如图6所示(以θ=15°为例)。θ=30°和45°时的参数如表2所示。至此，本文建立了复杂锯齿拖拽体在全侵入运动情况下的拖拽阻力表达公式，且该公式中的av，az和Cp只是锯齿倾角的函数。换句话说，只要给定拖拽体的锯齿倾角，该公式就可以表达不同拖拽速度和不同侵入深度的拖拽阻力。

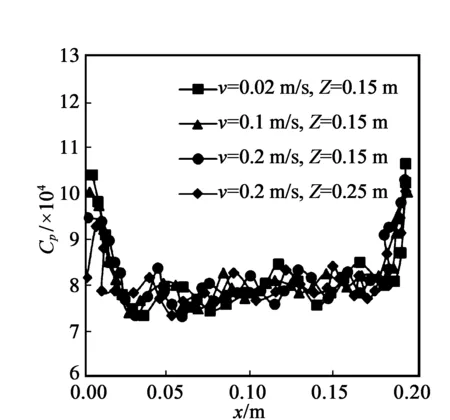
图6　锯齿形拖拽体C p值归一化

4结论

表2　 不同锯齿倾角下的速度影响参数和深度影响参数( θ=15°)

本文着眼于沙泳现象，用颗粒离散元的方法研究了锯齿形全侵入型拖拽体在颗粒材料中运动时的受力规律，主要得出了以下结论：

(1)对于完全侵入的拖拽体，拖拽阻力随着侵入深度的增大而增大，随拖拽速度的增大也相应增大。另外针对拖拽阻力，提出了速度影响参数、深度影响参数以及系统阻力系数，在此基础上对不同深度和不同拖拽速度情况下的拖拽力进行了归一化研究，结果显示除临近边界的情况外，其余部分的归一效果比较理想。

(2)速度影响参数和深度影响参数随着锯齿倾角的增大而增大，归一化系数随着锯齿倾角的增大而减小。

(3)无论锯齿的倾角如何，顺齿方向的拖拽体总是都到数值向上的升力。速度越大，顺齿方向的升力值越大。侵入深度对初始状态下的升力影响微弱，但是在稳定阶段以后侵入深度越大则升力越大。

(4)根据周期边界和非周期边界的对比发现，非周期边界下各种数值的波动现象很弱，数值相对非常稳定。

[参考文献]

[1]MALADEN R D,DING Yang,UMBANHOWAR P B,et al.Undulatory swimming in sand:experimental and simulation studies of a robotic sandfish[J].The International Journal of Robotics Research,2011,30(7):793-805.

[2]MALADEN R D,DING Yang,UMBANHOWAR P B,et al.2011.Mechanical models of sandfish locomotion reveal principles of high performance subsurface sand-swimming[J].Journal of The Royal Society Interface,8(62):1332-1345.

[3]MALADEN R D,UMBANHOWAR P B,DING Yang,et al.Granular lift forces predict vertical motion of a sand-swimming robot[C].In proceeding of zhe 2011 IEEE International Conference on Robotics and Automation(Shanghai,China,May 9-13),1398.

[4]孙其诚,王光谦.颗粒物质力学导论[M].北京:科学出版社,2009.

[5]POTIGUAR F Q,DING Yang.Lift and drag in intruders moving through hydrostatic granular media at high speeds[J].Physical Review E,2013,88(1):012204.

[6]GENG Jun-fei,ROGERT P B.Slow drag in two-dimensional granular media[J].Physical Review E,2005,71(1):011302.

[7]GRAVISH N,UMBANHOWAR P B,GOLDMAN D I,et al.Force and flow transition in plowed granular media[J].Physical review letters,2010,105(12):128301.

[8]MALADEN R D,DING Yang,LI Chen,et al.Undulatory swimming in sand:Subsurface locomotion of the sandfish lizard[J].Science,2009,325(5938):314-318.

[9]GOLDSMITH Jonathan,GUO Hong,HUNT S N,et al.Drag on intruders in granular beds:A boundary layer approach[J].Physical Review,2013,88(3):030201.

[10]PERCIER B,MANNEVILLE S,MCELWAINE J N,et al.Lift and drag forces on an inclined plow moving over a granular surface[J].Physical Review E,2011,84(5):051302.

[11]GUO Hong,GOLDSMITH J,DELACRUZ I,et al.Semi-infinite plates dragged through granular beds[J].Journal of Statistical Mechanics:Theory and Experiment,2012(7):07013.

[责任编辑：张存凤]

DEM simulation on sand swimming of sawtooth-shaped intruder

GUO Hong1,2,CHEN Xi1,LI Jun1,LUO Ya-sheng2,HU Hai-jun2

(1.School of Civil Engineering and Architecture, Shaanxi University of Technology,Hanzhong 723000, China2.College of Water Resources and Architechural Engineering, Northwest A&F University,

Yangling 712100, China)

Abstract:In order to investigate the drag and lift forces applied on the sawtooth-shaped intruder moving in the granular media, the DEM simulation is conducted to analyze the effect of inclined angle, immersion depth, velocity and boundary condition on drag and lift forces. The results show that the drag and lift forces are increasing with inclined angle. And the drag force is growing with the immersion depth and moving velocity. At last, the predicted model for drag forces are built. The generalized results show that, the other parameters can be confirmed based on the known inclined angle. And the formula can describe the drag force of different velocities and immersion depths.

Key words:granular flow;sand swimming;drag and lift forces