惯性测量单元误差标定

惯性测量单元误差标定

马帅旗

(陕西理工学院 电气工程学院， 陕西 汉中 723000)

[摘要]针对低成本惯性测量单元标定中的速度和精度问题，建立了惯性测量单元的误差模型，提出了一种针对惯性测量单元零偏、标度因数和安装误差角的标定方法。利用6状态法标定出加速度计参数，利用4状态法标定出了陀螺参数。对标定后的惯性测量单元进行试验测试，结果表明，标定后惯性测量单元的测量精度满足预期要求，标定方法正确、有效。

[关键词]惯性测量单元；标定；零偏；标度因数；安装误差

[文章编号]1673-2944(2015)05-0031-05

[中图分类号]V241

收稿日期：2015-02-01

基金项目：陕西理工学院科研基金资助项目(slgky13-46)

作者简介：马帅旗(1977—)，男，陕西省乾县人，陕西理工学院讲师，硕士，主要研究方向为智能控制、新能源发电。

惯性测量单元(IMU)是一种由三轴加速度计、三轴陀螺和三轴磁力传感器等组成的惯性测量器件，主要用于测量飞行器3个自由度的角速率、加速度和磁航向等信息。由于采用MEMS设计和系统集成方法，惯性测量单元具有重量轻、体积小、成本低、可靠性高等优点，在军事及民用领域得到了广泛应用[1-2]。惯性测量单元的测量精度不仅与惯性测量组件自身检测精度有关，也与加工工艺、安装精度有关，因而对惯性测量单元进行标定和误差补偿的研究具有重要意义。惯性测量单元的标定方法主要有传统的基于转台的多位置、角速率标定方法和现场多位置标定方法[3-4]。文献[5-6]在24位置标定方法的基础上，给出消除了不对北的陀螺标定方法。传统的标定方法以高精度转台为测试基础，标定过程非常复杂，而现场标定不仅能够减少工作量，而且能有效提高标定精度。文献[7-8]结合传统的静态多位置和速率标定方法，给出基于双轴旋转机构的6位置标定方法，该方法求解标度因子和安装误差较为方便，但在求解常值漂移时步骤较为繁琐。

本文对惯性测量单元的误差源进行分析，建立了误差模型。提出一种基于加速度计和陀螺的改进标定方法，并在三轴转台上对惯性测量单元进行相关测试，测试结果表明，标定结果满足预期要求，标定方法合理、可行。

1惯性测量单元误差模型

如图1所示，OXnYnZn为正交坐标系，OXbYbZb为惯性测量单元的坐标系，理想的陀螺和加速度计的3个轴向分别安装于3个正交面上，构成右手坐标系。但由于陀螺、加速度计自身工作原理、结构，以及集成制造、安装等因素影响，导致惯性测量单元中加速度计与陀螺的输入坐标轴之间不能正交，与正交坐标系之间存在6个安装误差角θxy、θxz、θyx、θyz、θzx、θzy。传感器标定的目的就是补偿输出值与测量值之间的标定因子，补偿零点偏移误差，补偿由加工精度、装配工艺等原因引起的安装耦合误差。

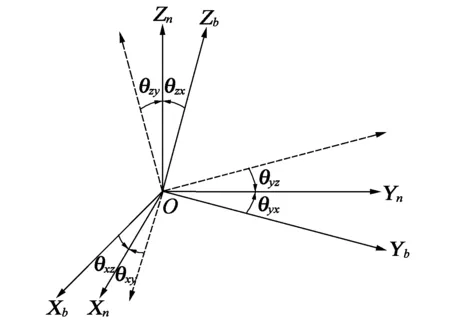
图1　非正交坐标系下安装误差角

1.1　加速度计误差模型

加速度计输出数据受到坐标系中轴系的正交性、安装精度及环境温度影响，会引起加速度计的零偏、标度因子、安装误差角和噪声等发生变化，因此加速度计的输出模型为

(1)

其中ag=[agx,agy,agz]T为敏感轴测量加速度矢量，a=[ax,ay,az]T为真实比力矢量，Sa为非线性刻度因子，Na为非正交矩阵，Da为常值漂移(零偏)，δa为陀螺噪声误差，考虑到δa对标定结果的影响较小，忽略噪声误差对测量结果的影响。令C=I+Sa+Na，则式(1)可以表示为

(2)

其中，Cyx、Czx为敏感轴xg安装误差角θxy、θxz的耦合系数，Cxy、Czy为敏感轴yg安装误差角θyx、θyz的耦合系数，Cxz、Cyz为敏感轴zg安装误差角θzx、θzy的耦合系数，Cxx、Cyy、Czz为敏感轴xg、yg、zg标定系数，Dax、Day、Daz是加速度计敏感轴xg、yg、zg的常值漂移(零偏)。

1.2　陀螺误差模型

陀螺输出数据受到坐标系的正交性、安装精度及环境温度影响，会引起陀螺的零偏、标度因子、安装误差角和噪声等发生变化，因此陀螺的输出模型为

(3)

其中ωg=[ωgx,ωgy,ωgz]T为敏感轴测量角速度矢量，ω=[ωx,ωy,ωz]T为真实角速度矢量，Sω为线性刻度因子，Nω为非正交矩阵，Dω为常值漂移(零偏)，δω为陀螺噪声误差，考虑到δω对标定结果的影响较小，忽略噪声误差对标定的影响。令K=I+Sω+Nω，则式(3)可以表示为

(4)

其中，Kyx、Kzx为敏感轴xg安装误差角θxy、θxz的耦合系数，Kxy、Kzy为敏感轴yg安装误差角θyx、θyz的耦合系数，Kxz、Kyz为敏感轴zg安装误差角θzx、θzy的耦合系数，Kxx、Kyy、Kzz为敏感轴xg、yg、zg标定系数，Dωx、Dωy、Dωz是陀螺敏感轴xg、yg、zg的常值漂移(零偏)。

2惯性测量单元标定

2.1　加速度标定方法

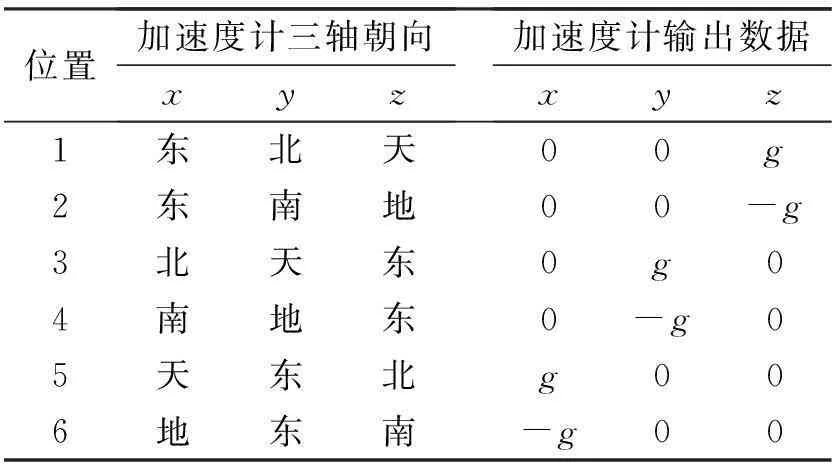
表1　加速度计6位置标定

在自然状态下，加速度计除了受重力加速度和地球自转外，不承受任何外加的力和角速度输入影响。加速度计标定采用静态多位置标定方法，将惯性测量单元分别旋转至如表1所示的6个不同位置，依次记录每一个位置输出的三轴加速度计输出数据，标定加速度计的零偏、标度因数和安装误差。

(5)

假设agi表示加速度计i轴测量值，ai j表示加速度计i轴向在j位置时的实际值，则在位置1、2处加速度计的实际值分别为ai1=[0,0,g]T，ai2=[0,0,-g]T。由加速度计误差模型可得

(6)

(7)

由式(6)、式(7)可得

(8)

在3、4位置加速度计的实际值分别为ai3=[0,g,0]T，ai4=[0,-g,0]T，依据上述方法可得

(9)

在5、6位置加速度计的实际值分别为ai5=[g,0,0]T，ai6=[-g,0,0]T，依据上述方法可得

(10)

因此，依据式(2)、(5)、(8)、(9)、(10)，可以获得加速度计误差标定模型为

2.2　陀螺标定方法

陀螺的标度因数和安装误差可以通过多位置法进行标定。为了尽量减少标定状态，初始标定时使陀螺的敏感轴指向东向或西向，则地球自转速率在该轴向的分量为零。依此原则，从24个状态中优选出4种状态进行陀螺标定。将惯性测量单元旋转至表2所示的4个不同位置，依次记录3个轴向陀螺的输出数据，标定陀螺的零偏、标度因数和安装误差。

表2　陀螺4位置标定

求取4个位置下陀螺输出数据的平均值 ，则陀螺的零偏为

(11)

陀螺在位置1的理想输入和输出分别为[0,ωecosφ,ωesinφ]T和[ωx1,ωy1,ωz1]T，在位置2的理想输入和输出分别为[0,-ωecosφ,ωesinφ]T和[ωx2,ωy2,ωz2]T，其中ωe为地球自转角速率，φ为当地地理纬度。依据陀螺误差模型，陀螺在位置1和位置2的输入、输出关系表示为

(12)

(13)

由式(12)、式(13)可得

(14)

陀螺在位置3的理想输入和输出分别为[ωecosφ,0,-ωesinφ]T和[ωx3,ωy3,ωz3]T，在位置4的理想输入和输出分别为[-ωecosφ,0,-ωesinφ]T和[ωx4,ωy4,ωz4]T。依据陀螺误差模型，陀螺在位置3和位置4的输入、输出关系表示为

(15)

(16)

由式(15)、式(16)可得

(17)

由位置1、2、3和位置4联合求解可得

(18)

因此，依据式(4)、(11)、(14)、(17)、(18)，可以获得陀螺误差标定模型为

3测试

惯性测量单元标定时，以高精度三轴转台性能参数为基准进行标定，该三轴转台角位置定位精度为±10″，最小角速度为±10(°)/s，速度分辨率为0.001(°)/s。将惯性测量单元安装于三轴转台内框的固定板上，使陀螺的敏感轴x、y、z轴与转台的3个转动轴平行。利用数据记录模块接收陀螺和加速度计输出的数据帧，并将数据帧写入SD卡。待试验结束后，从SD卡中读出数据帧并解算陀螺和加速度参数，进行惯性测量单元标定。

本文未对加速度补偿后的效果进行单独测试，而是结合陀螺进行姿态解算，依据解算后的姿态数据检验是否满足预期标定要求。试验时，通过三轴转台上位机软件设置三轴转台以一定的角速率旋转，先设定三轴转台滚转角依次为0→-15→30→0→-30→0→45→0(°)，再设定三轴转台俯仰角依次为0→30→0→-45→-30→45→30→0(°)，最后设定三轴转台偏航角依次为0→-5→10→-10→15→-15→20→-20→25→-25→30→-30→35→-35→40→-40→45→-45→50→-50(°)。记录试验过程中经标定后的三轴加速度数据、陀螺仪数据，然后进行姿态解算，获得滚转角、俯仰角和偏航角试验曲线如图2、3、4所示。其中，图2为转台滚转角设定值与经过标定后的滚转角曲线；图3为转台俯仰角设定值与经过标定后的俯仰角曲线；图4为转台偏航角设定值与经过标定后的偏航角曲线。从图2、3、4中可以看出，标定后的惯性测量单元的姿态角能够快速跟踪设定值，系统零偏较小，俯仰角和滚转角跟踪精度较高，偏航角跟踪精度角度略低，但二者之间稳态偏差小于1.5°，满足试验预期要求。

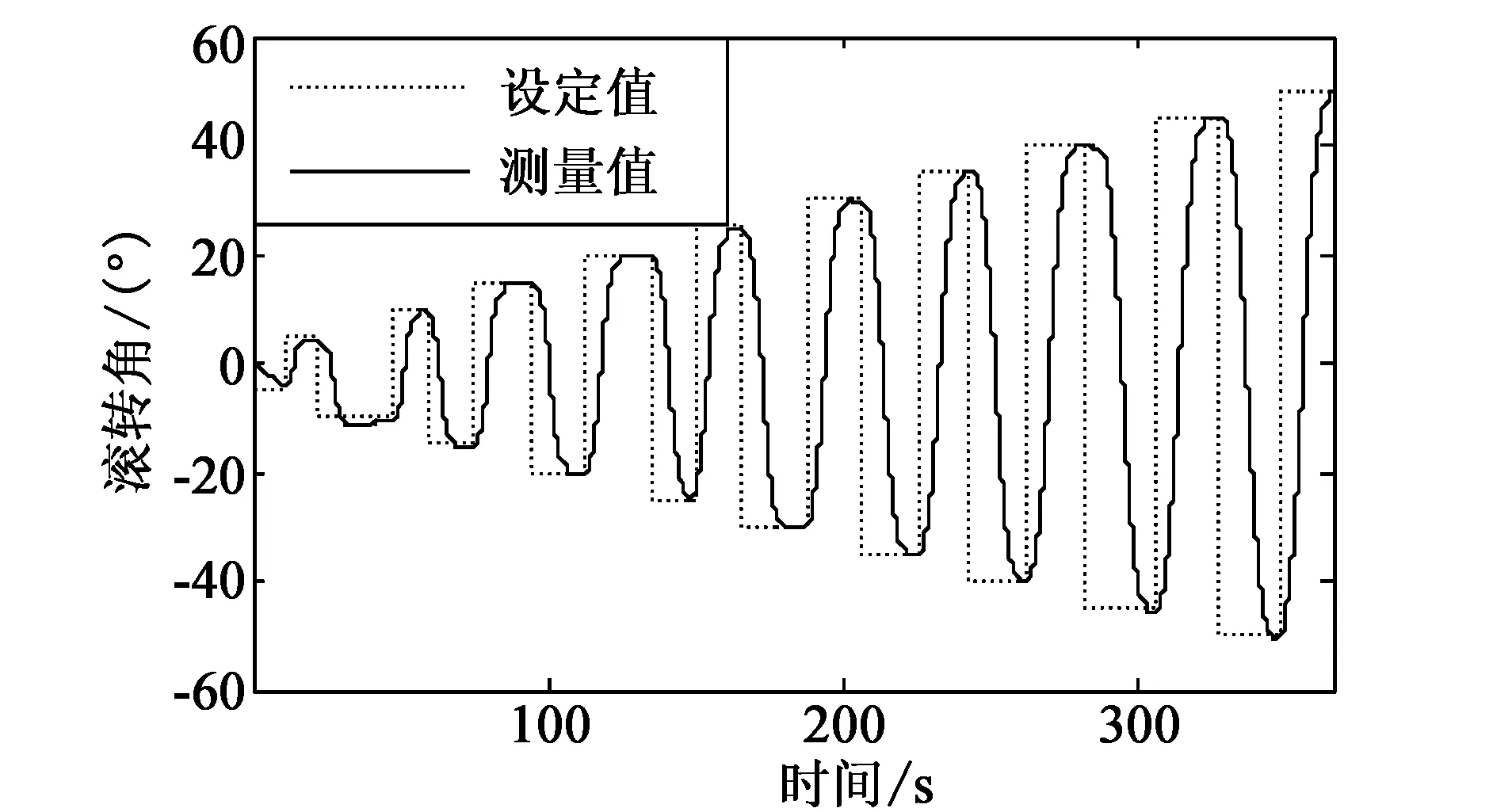
图2　标定后的滚转角设定值及测量值

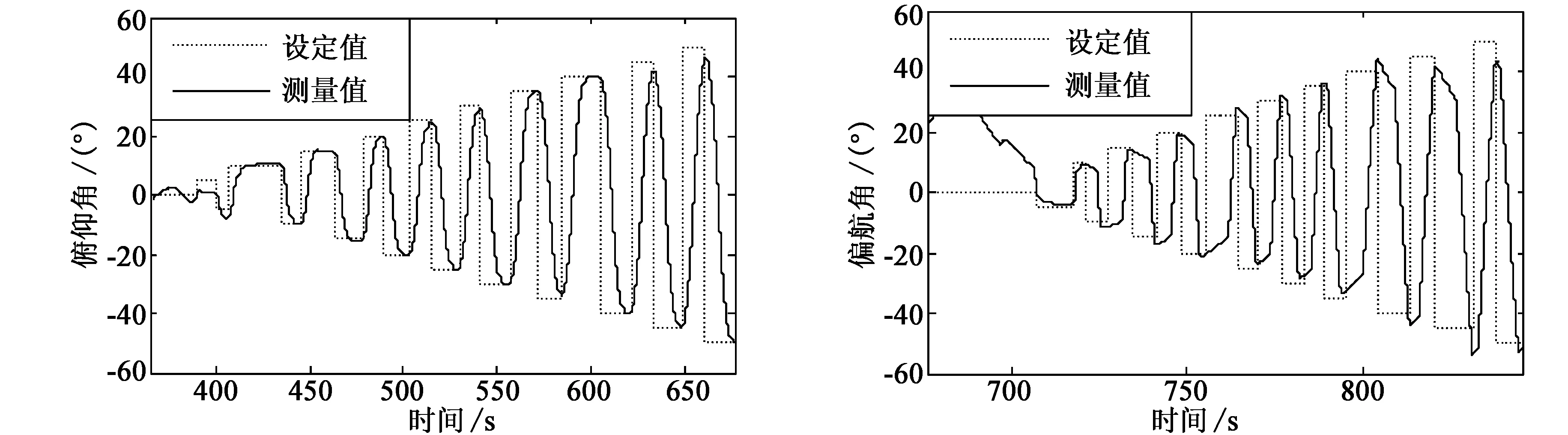
图3　标定后的俯仰角设定值及测量值　　　　图4　标定后的偏航角设定值及测量值

4结束语

本文提出了一种针对低成本惯性测量单元零偏、标度因数和安装误差角等标定方法，简化了标定过程，提高了标定效率。并将该标定方法应用于惯性测量单元，满足了预期试验要求，验证了该补偿方法的正确性和有效性。可以建立刻度因子温度模型、零偏温度模型，进一步提高标定的准确性。

[参考文献]

[1]彭孝东,陈瑜,李继宇,等.MEMS三轴数字陀螺仪标定方法研究[J].传感器与微系统,2013,32(6):63-65.

[2]FU Li,YANG Xi,WANG Ling-ling.A novel calibration procedure for dynamically tuned gyroscope designed by D-optimal approach[J].Measurement,2013,46(9):3173-3180.

[3]ARTESE G,TRECROCI A.Calibration of a low cost MEMS INS Sensor for an Integrated Navigation system[C].ISPRS2008,Beijing:ISPRS,2008:37,877-882.

[4]AYDEMIR G A,SARANLI A.Characterization and calibration of MEMS inertial sensors for state and parameter estimation applications[J].Measurement,2012,45(5):1210-1225.

[5]SCHOPP P,KLINGBEIL L,PETERS C,et al.Sensor Fusion Algorithm and Calibration for a Gyroscope-free IMU[J].Procedia Chemistry,2009,1(1):1323-1326.

[6]查峰,许江宁,覃方君.一种高精度无定向的光纤陀螺IMU转停标定方法[J].中国惯性技术学报,2011,19(4): 387-392.

[7]党建军,罗建军,万彦辉.基于单轴速率转台的捷联惯测组合标定方法[J].航空学报,2010,31(4):806-811.

[8]吴旭,孙枫,陈军.FOG双轴旋转六位置现场标定方法[J].传感器与微系统,2012,31(9):50-53.

[责任编辑：魏 强]

Calibration algorithm for inertial measurement unit

MA Shuai-qi

(School of Electrical Engineering, Shaanxi University of Technology, Hanzhong 723000, China)

Abstract:In terms of the issue of precision and calibrated speed in low cost micro inertial measurement unit, an error calibration model of gyroscope and accelerometer was built, and calibration algorithm was proposed to compensate for the bias, scale factor and misalignment angle. The accelerator’s parameters were estimated by six states method, and gyroscope’s parameters were estimated by four states method, and test experiment was carried out after calibrated. The experiment results show that expected precision has been achieved, and the availability and validity of the calibration algorithm was verified.

Key words:IMU;calibration;bias;scale factor;misalignment