一种改进的基于FXRLS的反馈式振动主动控制方法*

刘锦春 　季立军　何其伟　楼京俊　李海峰 　霍志国

(海军工程大学动力工程学院1)　武汉　430033)　(92711部队2)　青岛　266405)　(91285部队3)　大连　116041)

一种改进的基于FXRLS的反馈式振动主动控制方法*

刘锦春1)季立军2)何其伟1)楼京俊1)李海峰1)霍志国3)

(海军工程大学动力工程学院1)武汉430033)(92711部队2)青岛266405)(91285部队3)大连116041)

摘要：在实际的振动主动控制中，由于条件限制无法获得较为精确的参考信号，通常会导致会产生控制性能的下降.针对这类问题，文中在一种FXRLS主动控制算法的基础上，进行了改进，通过归一化技巧，提出了一种改进基于FXRLS算法的反馈式振动主动控制算法，相比原先的振动主动控制算法，它具有较强的鲁棒性能，能够有效处理此类的参考信号频率与振源信号频率不精确引起的性能下降的问题.通过对此算法的研究和仿真分析，验证了该振动主动控制算法能够在无法获得较为精确的参考信号时，有效进行振动主动控制.

关键词：振动主动控制; FXRLS; 参考信号

刘锦春(1987- )：男，博士，主要研究领域为振动噪声控制

0引言

舰船的振动噪声是影响舰船生命力的重要因素.因而有效隔离振动噪声的传播成为控制舰船振动噪声的重要手段.隔振成为被动隔振的传统隔振手段，能够有效抑制高频的振动，而其在低频减振领域存在着明显的缺点.振动主动控制作为有效抑制振源振动传播的有效手段，一直以来受到国内外研究学者的重视.相比被动隔振传统的控制方法，振动主动控制在低频减振方面存在较大的优势[1-3].周期性的动力机械设备是舰船设备中应用最为广泛的设备，如风机、泵等.这类周期性振动的主动减振存在着很多种方法，这些振动主动控制算法的基本原理都是产生一个方向相反，幅值相等的作用力抵消振源的振动.基于滤波器的自适应控制方法，由于其结构简单高效，因而在这类周期性设备的振动主动控制中得到了广泛的研究和应用.

FXLMS(filter-XLMS)和FXRLS (filter-X recursive least square)是这类自适应控制方法中的主要形式.相比FXLMS算法，FXRLS算法能够取得更为理想的控制效果.这类FXRLS前馈式振动主动控制方法，往往需要要求其参考信号的频率要和振动源的信号频率一致，才能够获得较为理想的控制效果.而在振动主动控制的应用中，往往由于条件的限制，获得的参考信号不够理想或者无法获得.由于舰船特殊环境限制，振源设备频率浮动、传感器(速度计)老化等因素使得获得的参考信号的频率与理想的参考信号频率存在着一定误差，控制效果受到很大的影响，甚至造成控制的失败.因此，对于这类无法获得较精确的参考信号周期性振动，迫切要求提出新的振动主动控制方法.目前，这已经为国内外研究的热点.通常的方法都是通过估计频率获得精确的参考信号后进行振动主动控制算法[4-6].国内张志谊等提出了基于子空间辨识的频率估计与经典FXLMS结合的自适控制方法，取得的良好的振动抑制效果.但是这2个部分是分割开的，在多频情况下，相互之间的计算复杂度差别较大，容易控制失败.张磊等提出了基于自适应陷波器进行频率估计的主动隔振方法.但这些方法中都是将算法分为2部分，先进行频率估计，然后进行FXLMS自适应控制.相比之下，Yegui Xiao等提出了的方法能够有效的将频率估计与FXLMS同时进行，取得良好的主动控制效果[7-9].类似于Yegui Xiao等人的方法，本文提出了一种新的振动主动控制方法，在经典的FXRLS算法的结构中，增加了频率更新和相位更新环节，从而实现参考信号的内部闭环生成；并采用归一化技巧，提高鲁棒性能，实现了在参考信号精度不佳的条件下，进行有效的振动主动控制的目的.

1经典的FXRLS主动控制算法

假设在振动主动控制中，需要控制的振动源信号为

(1)

式中：ωp为振动源信号中正弦信号频率分量的频率；系数Ap为正弦信号的幅值；φ为初始相位；v(n)为背景白噪声，其均值为零；方差为σ2.

传统的窄带FXRLS振动主动控制算法内容如下.

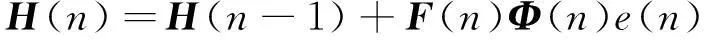
(2)

(3)

(4)

(5)

(6)

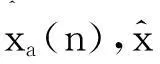
(7)

(8)

振动主动控制算法中用于抵消振源振动的次级力信号为

(9)

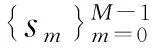
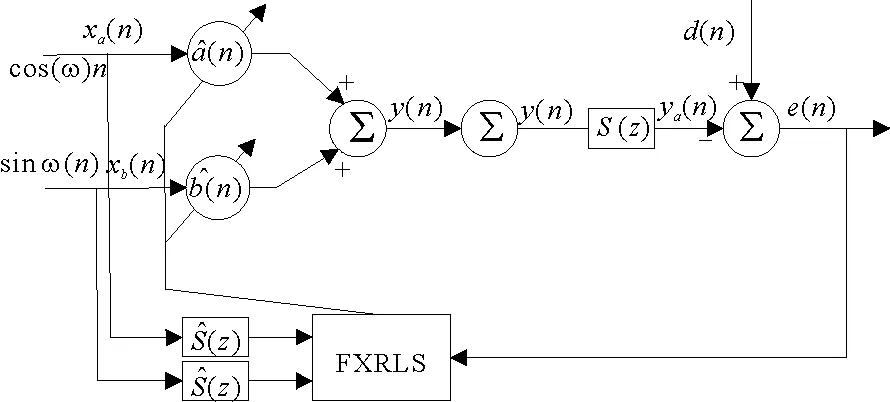
图1　经典的FXRLS算法

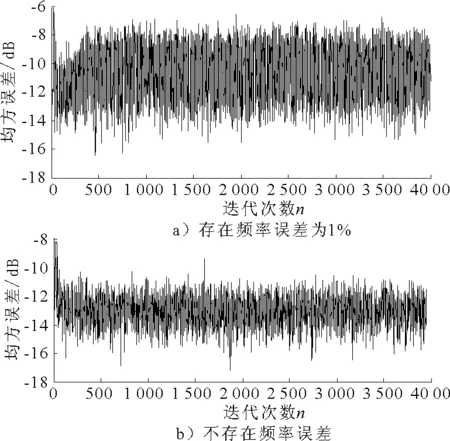
图2　当参考信号频率与振源频率存在误差时，FXRLS算法性能比较

由图2可见，一旦参考信号的频率与振源信号的频率发生偏移超过1%，就会导致控制算法性能严重下降,此时振动主动控制性能下降4 dB以上.

2基于FXRLS的反馈式振动主动控制算法

舰船设备由于其特有的工作环境，振源设备的频率偏移浮动是非常普遍,较容易造成参考信号的频率与振源设备频率的偏差，导致舰船的振动主动控制中控制效果的降低.为解决这类问题，在上述经典的窄带FXRLS振动主动控制算法的基础上，提出了一种改进的反馈式振动主动控制算法，算法内容详细如下.

(10)

(11)

(12)

(13)

(14)

(15)

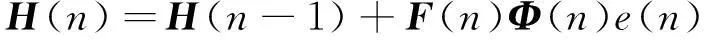
(16)

(17)

(18)

(19)

(20)

式中：c(n)为一个与参考信号频率相关的系数.它与生成的参考信号频率存在如下关系式为c(n)=-2cos(ω(n)).ω(n)为通过方程(10)～(13)生成的参考信号的频率.ω(0)为设置的参考信号的频率初值，为加快算法的收敛可以通过事先将ω(0)设为靠近振源频率附近的值.

根据梯度下降法，沿着梯度下降方向，推导得频率相关系数c(n)的更新公式为

(22)

式中：μc为频率相关系数c(n)的更新方程的步长因子，可以设置一个较小的正系数.

在上述算法中，xa,0(n)和xb,0(n)为经过二阶AR(autoregressive)模型进行自更新过程，通过归一化处理，从而获得幅值为1的参考正弦和余弦信号，使得系统更为稳定.通过引入频率相关系数c(n)，能够避免在传统算法中需要不停的计算正弦、余弦函数的缺点，有助于在实际应用中的推广.通过上述算法实现了参考信号的内闭环生成，为解决参考信号与振源信号频率发生偏移,提供了一种稳定有效的方案.算法结构见图3.

图3　基于FXRLS的反馈式振动主动控制算法

3仿真

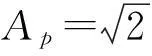
4结束语

文中针对在舰船振动主动控制中，参考信号频率与实际振源信号频率存在误差时，主动控制的效果降低的问题，提出了一种基于FXRLS的反馈式振动主动控制算法.通过参考信号内闭环非线性生成，克服以上缺点.分析和仿真表明该算法能够有效的解决由于参考信号精度下降造成的振动主动控制性能下降的问题.该算法在频率误差达到10%时，仍然能够有效的进行振动主动控制.在下一步的研究中需要进一步展开对此种算法的统计性能研究.

参 考 文 献

[1]张志谊，王俊芳，周建鹏，等.基于跟踪滤波的自适应振动控制[J].振动与冲击，2009，28(2):64-67.

[2]孙红灵.振动主动控制若干问题的研究[D].合肥：中国科学技术大学，2007.

[3]胡世峰,朱石坚,楼京俊,等.内模控制策略在混合隔振系统中的应用研究[J].武汉理工大学学报：交通科学与工程版,2010(4):684-688.

[4]王俊芳，张志谊.基于相关序列的在线频率估计方法[J].船海工程,2008(3):45-48．

[5]张磊，刘永光，付永领，等.基于自适应陷波器的主动隔振仿真研究[J].系统仿真学报,2005，17(1)：234-237．

[6]张国庆，王永，陈光.一类多频线谱振动的主动控制方法[J].南京理工大学学报：自然科学版，2005，29(z1)：37-40．

[7]YEGUI X,LIYING M,KHORASANI K.A filtered-X RLS based narrowband active noise control system in the presence of frequency mismatch[C].Circuits and Systems ISCAS IEEE International Symposium on,2005,260-263.

[8]KUO S M,ZHU S,WANG M.Development of optimum adaptive notch filter for fixed-point implementation in active noise control[C].Industrial Electronics,Control,Instrumentation,and Automation, Proceedings of the 1992 International Conference on,1992：1376-1378.

[9]YEGUI X,LIYING M,KHORASANI K,et al.A new robust narrowband active noise control system in the presence of frequency mismatch[J].Audio,Speech,and Language Processing,IEEE Transactions on,2006,14(6):2189-2200.

中图法分类号：O32; X966

doi:10.3963/j.issn.2095-3844.2015.01.009

收稿日期：2014-08-10

An Improved Method of Feedback Active
Vibration Control Based on FXRLS Algorithm
LIU Jinchun1)JI Lijun2)HE Qiwei1)LOU Jinjun1)LI Haifeng1)HUO Zhiguo3)

(CollegeofPowerEngineering,NavalUniversityofEngineering,Wuhan430033,China)1)

(No. 92711Army,Qingdao266405,China)2)(No.91285Army,Dalian116041,China)3)

Abstract：The unavailability of the precise reference signal will cause the performance degeneration of active vibration control in practical implementations. It is commonly implemented by identifying the frequency of the reference signal. To tackle the problem of performance degradation,an improved method of active vibration control based on Filter-X Recursive Least Square (FXRLS) algorithm is proposed by normalizing technique in this paper. It is demonstrated that the algorithm can deal with the performance degradation caused by the frequency mismatch between the reference signal and primary signal. It is analyzed and validated that the algorithm can effectively perform well with the presence of unavailable precise reference signal.

Key words：active vibration control; FXRLS; reference signal

*国家自然科学基金青年科学基金项目(批准号：51009143)、高等学校全国优秀博士学位论文作者专项资金项目(批准号：201057)资助