面向任务的船用核动力装置使用可用度仿真

2016-01-07段孟强,戴俊,马俊

交通科技 2015年2期

面向任务的船用核动力装置使用可用度仿真

段孟强戴俊马俊

(海军驻431厂军事代表室葫芦岛125005)

摘要以任务为牵引，结合船用核动力装置使用特点和工作特性，考虑系统内部备用单元的使用转换，设备的故障与修复以及保障延误，建立了其使用可用度(A0)的仿真模型和仿真流程，在建立系统使用可用度评价指标基础上，基于Monte-Carlo方法对装置进行了任务条件下的使用可用度仿真计算。研究表明，建立的仿真模型能够量化装置使用可用性评价指标，分析结果可为查找系统薄弱环节、改进系统可用性设计提供依据。

关键词船用核动力装置使用可用度Monte-Carlo方法不确定性分析

DOI10.3963/j.issn.1671-7570.2015.02.051

收稿日期：2015-01-04

不同于导弹或军用飞机，船用核动力装置在任务执行期间具有一定的可维修性，单纯的可靠性研究并不能真实反映装置的任务完成能力，须要通过可用性来衡量。使用可用度A0作为一项关于可靠性维修性保障性[1](RMS)的综合参数，属于战备完好性范畴，能反映系统执行任务的持续能力。因此，可以通过对装置典型任务剖面下的A0分析来反映其薄弱环节，并反馈到装置的设计与使用管理上。

对于复杂的船用核动力装置A0分析，采用解析法会十分繁琐，有一定限制[2]，不适用；采用试验方法来获得所需的数据代价高昂，又要面临核安全风险，且由于故障的随机性，现有的数据积

累无法提供全面的信息。文献[3-4]指出，蒙特卡洛(Monte-Carlo)方法能解决这一随机性问题，对基本随机变量的分布及其相关性没有任何限制，只要抽样次数足够多，蒙特卡洛方法的计算结果可以认为是“精确”的。因此，基于Monte-Carlo方法[5]，对设备的故障与修复时间等进行随机抽样[6]，并应用相应的统计模型获得离散解，是解决这些问题的较理想方法，能获得较全面的信息。

1仿真模型

1.1　仿真影响因素分析

A0是系统RMS的综合反映。在对象上，影响仿真的因素[7]涉及反应堆、一回路系统、二回路系统、推进轴系等，诸多设备之间通过功能接口与物理接口关系、控制关系相互保障和制约，构成一个有机整体；在参数上，影响其仿真的因素主要包括设备的固有可靠性和固有维修性在内的设计参数，以及与使用相关的参数(如系统允许停用时间、维修能力、技术保障和使用规则等)。

Over Draft Monitoring System Design and Implementation of the Ship

WangRujun1，ChenJun1，XiongHui1，ChenLiang2

(1.ChangjiangMaritime Safety Administration, Wuhan 430016, China;

2.Shenzhen Graduate School of Harbin Institute of Technology, Shenzhen 518055, China)

Abstract：In recent years, the ship's overload and overdraft phenomenon in the Yangtze River Waterway is more and more serious, the situation is not optimistic. The current management approach is single, which requires the maritime sector investing huge human, material and financial resources; and the effect is not very satisfactory. In response to these problems, based on laser radar freeboard height measurement method to quickly detect the ship's draft, and in the area of waters Yueyang Maritime Safety Administration implements demonstration application. The results showed that the proposed system made a good job in measurement accuracy, system response time, system suitability and timeliness.

Key words: overdraft ship; detection; freeboard; Laser radar

为了方便仿真的进行，作如下假设。

(1) 任务执行之前，严格检查装置，并对潜在故障设备进行更换性维修，可不考虑设备性能退化问题。假设各设备只有“故障”和“正常”2种状态，初始状态良好，均能正常工作。

(2) 设备故障相互独立，不考虑相关故障；设备故障与人员无关，忽略人员因素。

(3) 对于艇员级维修，故障修复时间和保障时间通常相对很短，对整个任务的执行影响不大。为了研究问题的方便，假定连续运行设备的故障修复时间服从指数分布，保障延误时间为常数。

(4) 维修人员和备件数目等维修资源充足，故障出现后，立即维修。对于任务执行时由于条件限制某些维修任务无法完成时，可认为维修时间无限长，但不计算在平均故障修复时间之内；能够维修的设备，修复时间均在允许修复时间之内。

(5) 分析的基准层为设备级，分析时称为“单元”。

(6) 抽样时，按照机电设备服从威布尔分布，电子设备服从指数分布，机械设备服从正态分布处理。

1.2　仿真模型构建

(1) 任务模型。假设船用核动力装置以低工况和中等工况连续运行，装置中各设备按照要求投入使用。当任务期间缺乏对故障单元的维修能力或维修时间超过任务中系统的允许停用时间，则表明任务失败。

(2) 可靠性框图模型。建立典型船用核动力装置在规定任务下的可靠性框图。其中，一回路系统(1～23单元)可靠性框图见图1，二回路及轴系系统(24～79单元)可靠性框图见图2。

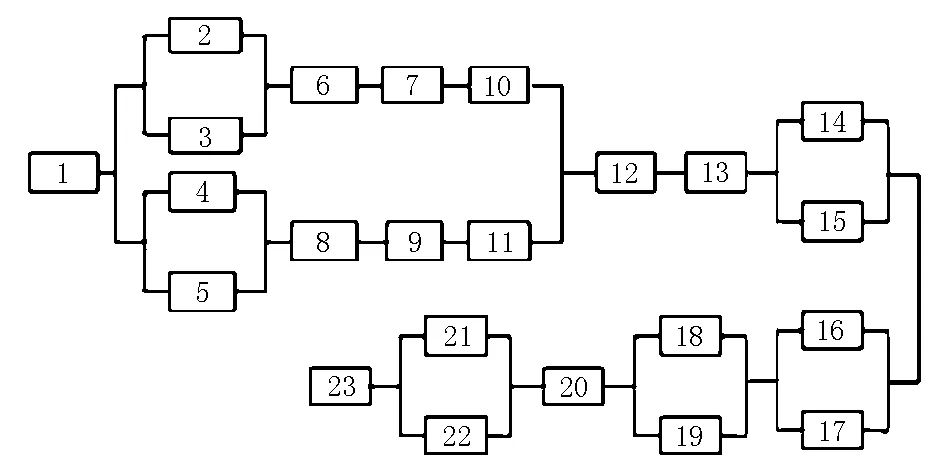
图1一回路系统可靠性框图

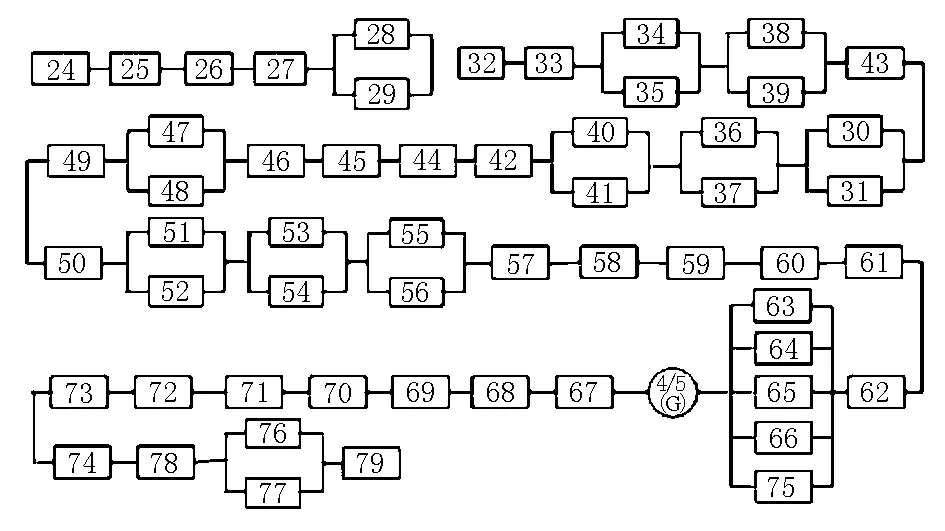
图2　二回路及轴系可靠性框图

(3) 离散事件模型。系统和装置的状态由设备状态决定。设备 “故障”和“正常”2种状态是不会发生连续变化的，且具有无后效性，因此系统和装置的状态是一个时间连续、状态离散的马尔科夫过程；记录设备状态发生变化的时刻，建立事件表，结合可靠性框图模型，就能获得每一时刻系统状态的描述。

(4) 统计模型。建立设备层、系统层、装置层3级评价装置A0指标体系(包括使用可用度、任务成功率、平均可用时间、平均故障间隔时间、平均致命故障间隔时间、平均致命故障次数、平均故障次数、平均故障修复概率、设备故障次数等)，统计结果通过该体系评价指标的对应参数来反映影响装置任务的执行情况。几个重要参数定义如下。

① 任务成功率。在设定的任务模型当中，系统任务成功次数占总仿真次数的百分比，就是系统在该任务下的任务成功率R。

② 任务期间的系统平均可用时间MUT和平均致命故障间隔时间MTBF。这里定义致命故障为会导致系统功能失效的故障。记TR(i,j)为第i次任务过程期间发生的第j次故障的不可用时间；t为此故障发生时刻；TBKY(i)为系统除发生致命不可修复故障的系统不可用时间；TZMR(i,a)为发生致命可修复故障产生的系统不可用时间，见图3。

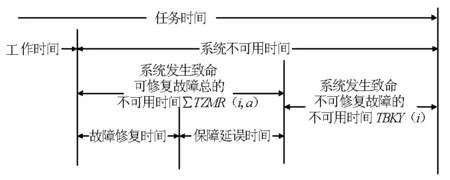
图3　任务时间分解图

当故障不可修复时，对系统而言，若为非致命故障，启动备用设备，系统仍能继续使用；若为致命故障，则任务失败，令：TBKY(i)=24m-t，且TZMR(i,a)=0，当无致命性不可修复故障出现时，TBKY(i)=0。

当故障可修复时，TZMR(i,a)=TR(i,j)。

则系统平均可用时间为

式中：n为仿真次数；k为第i次任务过程中发生的致命故障次数；m为运行天数。

平均致命故障间隔时间为：

式中：FCS为致命故障总次数。

(3) 使用可用度。使用可用度A0可以定义为：在某一任务剖面中，系统能工作时间占总工作时间的比率。因而可以用公式表示为

2仿真流程和计算

2.1　仿真流程

对于上文给定的任务模型，装置的可靠性框图不变，因而不需要分阶段讨论，直接建立其仿真流程，见图4。

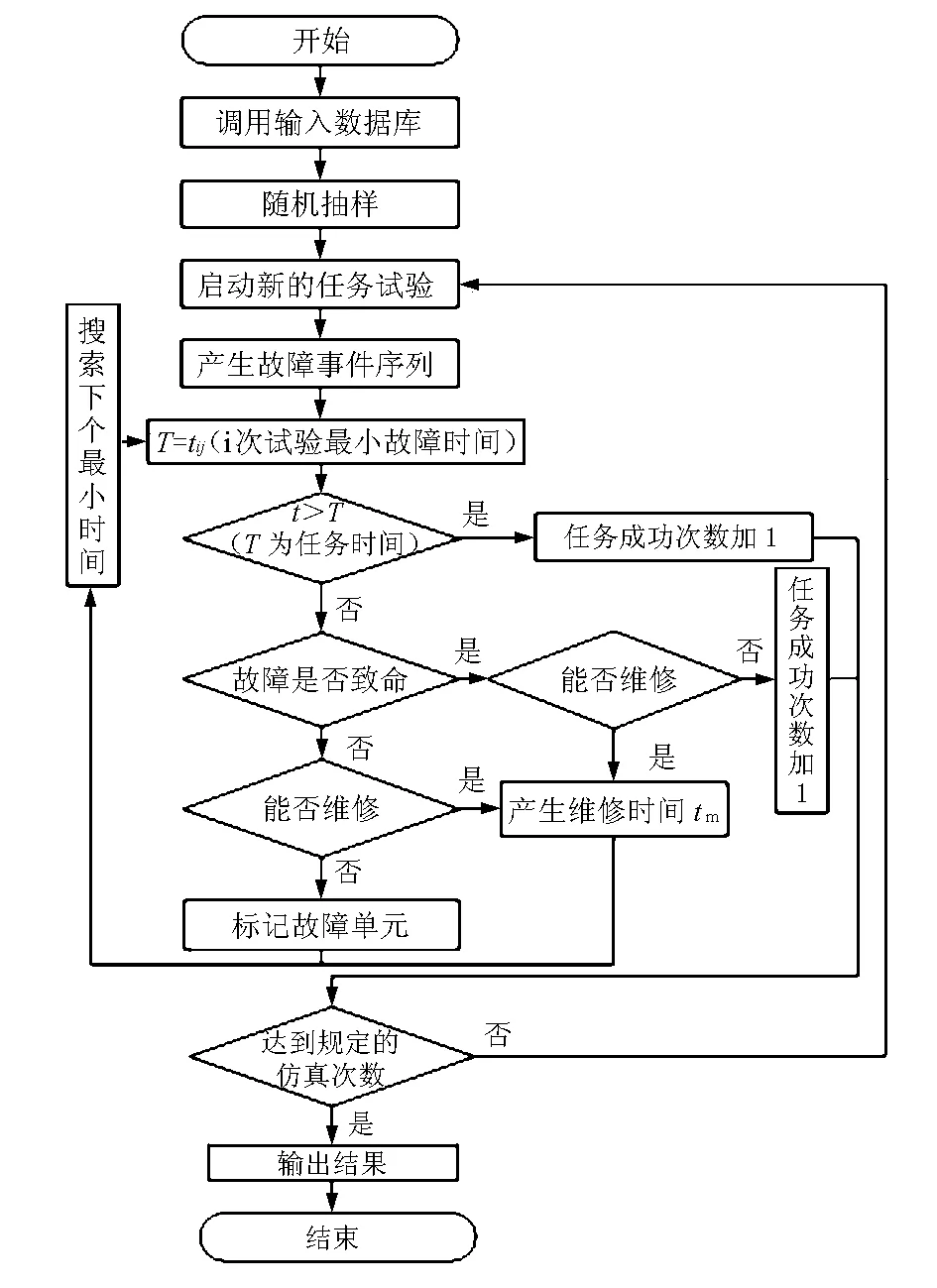
图4　使用可用度仿真流程图

2.2　仿真计算

基于Monte-Carlo方法，根据仿真流程图，编写计算机程序[8]，进行规定任务下船用核动力装置A0仿真。

首先，对所有单元的故障时间、修复时间，以及可修判断进行随机抽样，分别建立相应矩阵。设定仿真次数为N，而各值的抽样次数设为5N(即在一个任务周期内每个单元最多允许发生5次故障，故障次数可根据实际情况调整。为了加快运算速度，此值可以适当减小。

从仿真结果来看，发生故障最多的单元，每次任务的平均故障次数不超过1，因而该值设在3以上，只要程序运行不报错，都是允许的。

前N组故障数据作为仿真初始故障抽样值。选取故障时间矩阵的第i(i

3实例研究

在程序中输入相关数据(部分设备输入数据见表1)，仿真10 000次的统计结果见表2和表3。其中，可靠性数据在借鉴WASH-1400和西德GRS风险评价报告[9]，以及文献[10]的基础上进行一定处理而得到。船用核动力装置的二回路和轴系设备不作调整，在给定任务模型下，主系统设备特征寿命(或寿命中值)在计算结果的基础上再降低一个数量级，其他数据依据运行经验。主系统设备故障模式可修率的威布尔分布形状参数β取1.4。由于β=3～4时，其故障密度函数已经与正态分布近似，因此正态分布可用β=3.5的威布尔分布代替。

表1　部分单元输入参数

表2　输出结果统计

表3　部分单元故障结果统计

表3中选取故障信息统计的单元，既有服从威布尔分布的，也有服从指数和正态分布的；既有故障率较低的，也有故障率较高的；既有独立单元，也有并联单元，基本上能反映仿真中其他单元的故障信息。

从统计结果来看：①随着任务时间的增加，平均不可用时间急剧增加，平均故障间隔时间有所减少，但减少的幅度降低，而任务成功率和使用可用度降低的幅度基本不变；②服从威布尔分布的单元(单元1，530，40，60)随时间的增加故障次数先增后减(30～60 d内增加最多)；服从指数分布的单元(单元50)故障次数增加幅度基本不变；服从正态分布的单元(单元10)则不变；大部分单元服从威布尔分布，说明30～60 d这个时间段是故障密度较集中的一个阶段。

4结论

建立的A0仿真模型与算法在确定任务条件下能对装置运行状况进行预测，获得任务成功率、使用可用度等数据以及各设备在任务中的故障状况，为装置改进设计、提高效能提供理论参考。

将来可在本文基础上开展敏感性分析，研究单个部件失效对系统失效的影响和敏感性排序等问题，以及仿真预测结果的验证难题。

参考文献

[1]甘茂治,康建设,高崎.军用装备维修工程学[M].北京：国防工业出版社，2001.

[2]杨宇航.基于仿真的复杂武器系统任务可靠性评估与维修管理研究[D].北京：北京航空航天大学出版社，2002.

[3]郑兴国,郗曼丽.蒙特卡洛方法在复杂兵器可靠性综合评定中的应用[J].兵工学报:弹箭分册，1992(2):73-77.

[4]叶乃全,胡毓仁,陈伯真.超静定结构系统疲劳可靠性分析的蒙特卡洛方法[J].上海交通大学学报，1998，32 (11):8-12.

[5]徐志军，王平．基于蒙特卡洛方法的多散射修正模型[J].海军工程大学学报，2010, 27(6):50-54.

[6]杨为民，盛一兴.系统可靠性数字仿真[M].北京: 北京航空航天大学出版社，1990.

[7]程文鑫,陈立强,龚沈光,等.基于蒙特卡洛法的舰船装备战备完好性仿真[J].兵工学报，2006, 27(6):1090-1094.

[8]龚纯，王正林．MATLAB语言常用算法程序集[M]．北京：电子工业出版社，2008.